基于密度聚类和lp范数最小化的空中微动群目标盲源分离技术研究
2022-08-09孙惜媛顾鹏飞丁大志
温 柔,孙惜媛,何 姿,顾鹏飞,丁大志
(南京理工大学 电子工程与光电技术学院,南京 210094)
0 引言
雷达信号的目标识别技术在军事检测防御系统中意义非凡,盲源分离(blind source separation, BSS)是解决雷达系统中混叠信号的有效途径[1]。BSS最早是从“鸡尾酒会问题”引申而来,其本质上是一种功能强大的信号处理问题。该问题描述为:在若干个麦克风同时接收到若干个声源的情况下,从混合的麦克风信号中恢复出各个声源,欠定盲源分离(underdetermined blind source separation, UBSS)可以理解为麦克风数量小于声源数量。本文在雷达系统的背景下,从接收到的微动群目标的混合信号中分离出各目标的回波信号。
自1985年Herault和Jutten[2]首次提出至今,BSS一直是研究的热门方向,该领域中应用最广泛的是Comon提出的独立成分分析(independent component analysis, ICA)方法[3]。由于UBSS的不可逆性, ICA方法并不适用于此场景,因此Lewicki根据源信号的稀疏特性提出了稀疏分量分析方法(sparse component analysis, SCA)[4],成为欠定领域中的前沿方法并被广泛应用[5-6]。
2001年,Bofill和Zibulevsky基于SCA提出了经典的“两步法”[7],该方法的许多参数设置虽然在当时没有具体的理论支持,但仍具有重要的贡献和参考价值。一般来说,两步法首先通过未知的混合矩阵将若干个源信号混合得到回波信号,在该回波信号的基础上对混合矩阵进行估计,然后利用前面估计出来的混合矩阵分离出各源信号。在第一步中,文献[8]利用混合信号的局部协方差矩序列的非平稳特性,将混合矩阵估计转化为联合近似对角化(joint approximate diagonalization, JAD) 最小化模型,文献[9]将JAD最小化问题转化为张量分解问题。文献[10-11]使用合适的算法来检测单源点,利用稀疏的单源点并结合聚类算法进行混合矩阵估计。文献[12]提出了经典的K-means聚类方法用于估计混合矩阵,该方法主要的不足之处在于源信号的个数要已知,这并不符合实际情况。由于欠定情况下的解混操作没有唯一解,第二步将源分离问题建立为各种优化模型。最经典的方法为线性规划算法中的l1范数最小化方法和最短路径法[13-14],l1范数最小化方法要求源信号足够稀疏,最短路径法只适用于在两个观测通道的情况下,因此这些经典方法都具有非常大的局限性。文献[15]提出了一种改进的l1范数最小化方法,以最小化源信号中分量值较小的部分元素为目标函数,采用线性规划方法求解新的数学优化模型的精确解,实现源信号重构。文献[16]基于源的拉普拉斯分布假设,提出了一种基于lp范数的源分离优化模型,但是,当p小于0.75时,求得的解为局部极小值而非全局最优解。第二步的另一种经典方法是压缩感知理论,文献[17]在用压缩感知理论解决欠定盲源分离问题时提出了一种基于分层耦合的字典训练方法,通过对先验信息的分层训练,实现雷达信号的高精度重构。
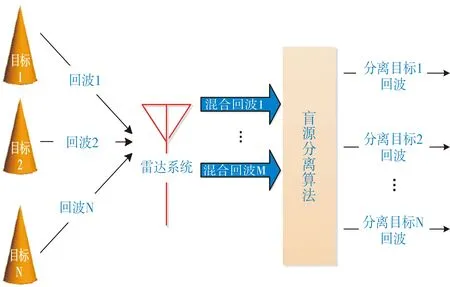
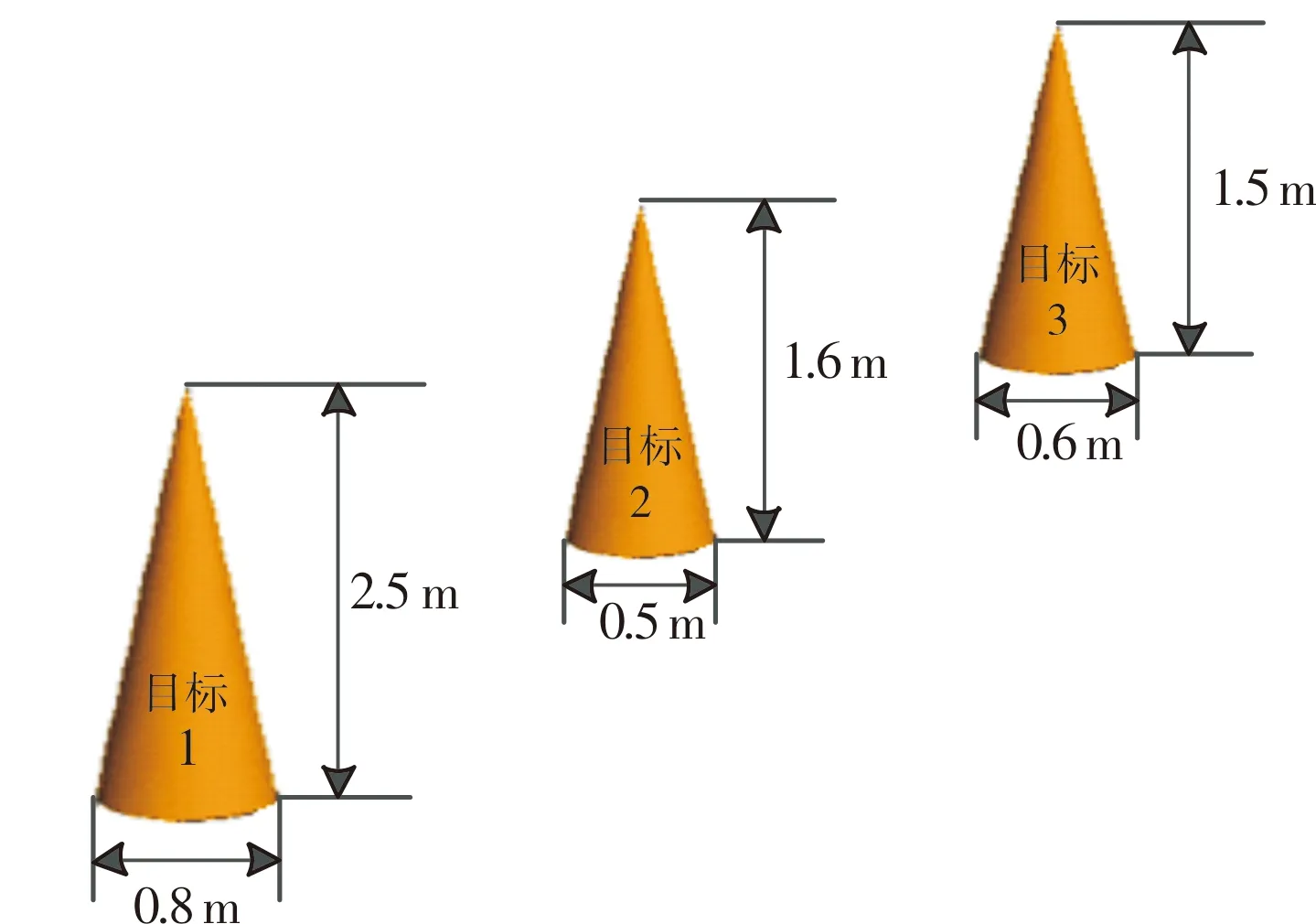
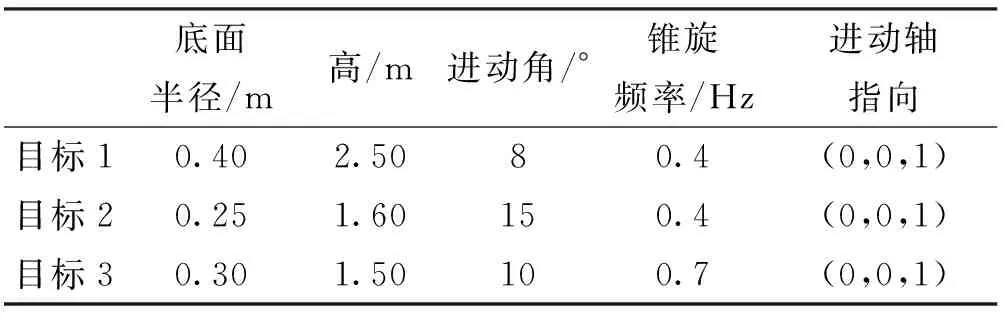
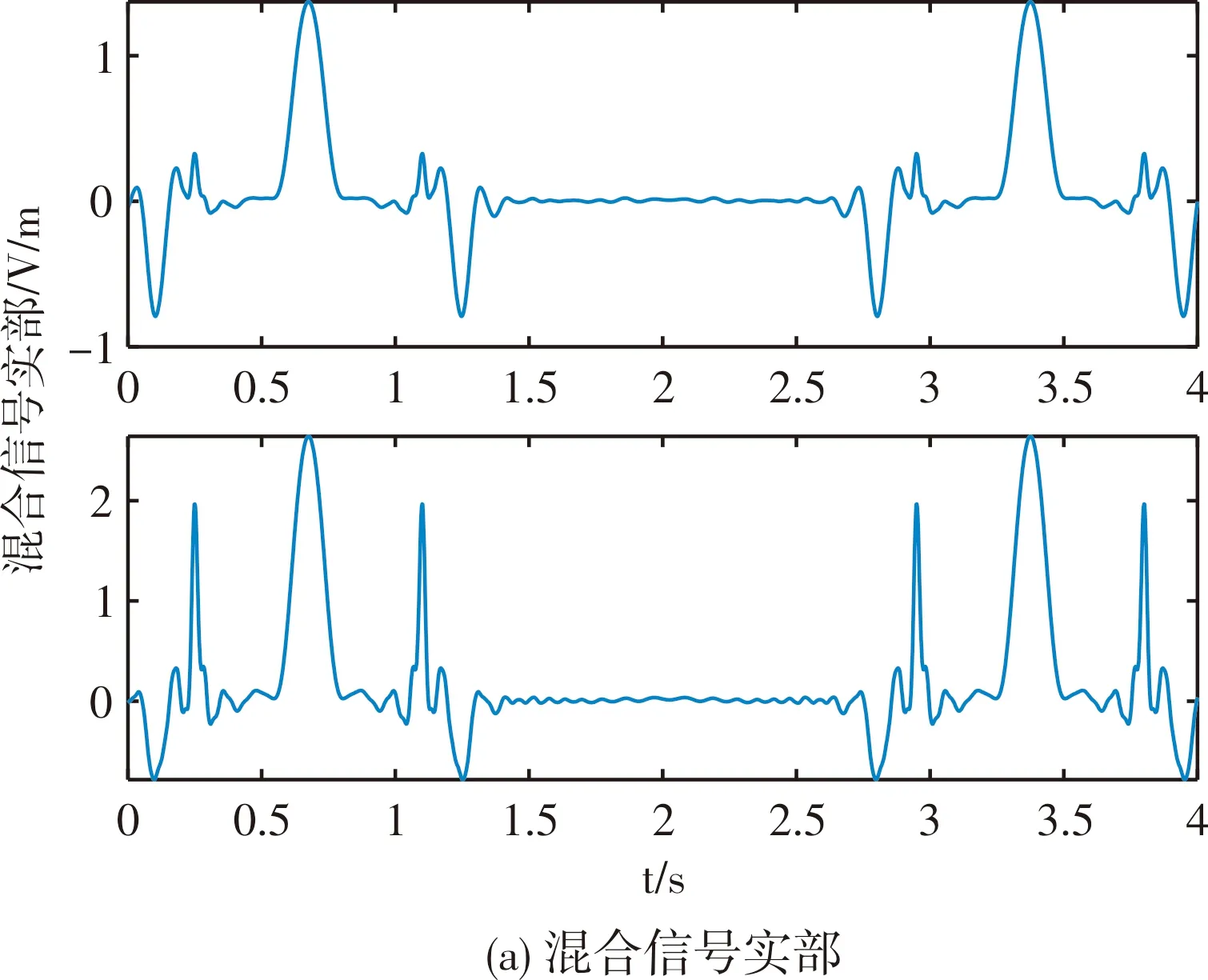
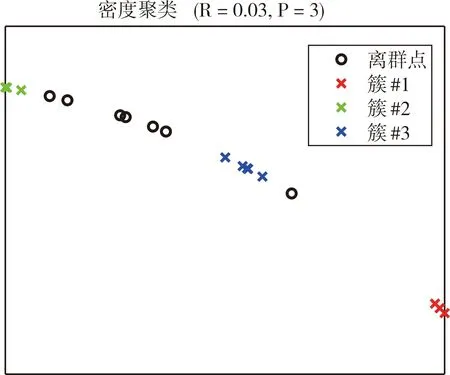
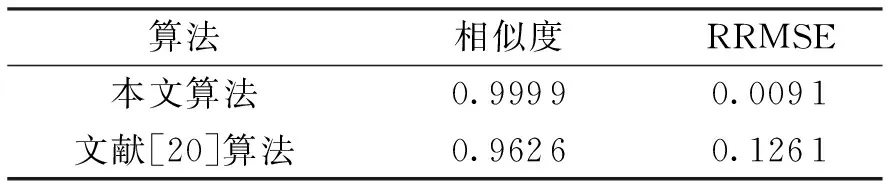
为解决上述问题,本文在“两步法”框架的基础上,以空中微动群目标为源信号[18],雷达接收的回波为混合信号,提出了一种改进的两阶段混合矩阵估计和源分离方法。第一步,利用混合信号的局部协方差序列,将混合矩阵估计问题转化为特征向量聚类问题。在聚类中,通过检查数据集中每点的R邻域来实现簇的分类。如果点I的R邻域中数据点的个数多于P,即I点周围密度较大时,则创建一个以I为聚类中心的簇,否则I点视为离群点,最后通过求得每一簇的均值来实现混合矩阵的估计。该方法优点在于不需要预先输入簇的个数,并能有效处理离群点。第二步,将源分离问题转化为基于lp范数(0 BSS的系统模型可以划分为线性和非线性两种混合模型[19],每种模型又分为瞬时、延时和卷积混合模型。本文主要研究的是线性瞬时混合模型。 在不考虑噪声的情况下,线性瞬时混合模型的BSS过程可以表示为: X(t)=HS(t) (1) Y(t)=WX(t) (2) 式(1)中,S(t)=[s1(t),s2(t),…,sN(t)]T为N维的未知源信号,H为M*N维的混合矩阵,X(t)=[x1(t),x2(t),…,xM(t)]T为M维的混合信号。式(2)中,W为N*M维的分离矩阵,Y(t)=[y1(t),y2(t),…,yN(t)]T为N维的分离信号。 以分离弹道中段的弹头群目标为研究对象,当地面雷达检测到多个目标的混叠回波时,为了获取目标的有用信息,需要从混叠回波中将每一个目标分离出来。如图1所示,显示了空中微动群目标的BSS模型图。该模型由M个雷达系统接收N个目标的回波,从而获得M个通道的混合信号,然后利用BSS算法分离出每一个目标的回波。 图1 BSS模型图Fig.1 The model diagram of BSS 为了解决上述模型的问题,本文的方法需要建立在两个假设前提下: 1) 混合信号的数量小于源信号的数量,也就是说需要在欠定的情况下,即M 2) 每个源信号需要存在局部优势[20-21],即在时域上至少存在一个子块是仅由一个源信号起主导作用的。在不同的微动参数,例如微动频率、微动形式等,以及不同的尺寸、样式下,弹头群目标的回波会存在局部优势,对于任意一个目标源信号仅需保证在某一时间段内占主导作用,即可将该信号从混合信号中分离出来。如图2所示,在三个源信号的电场实部图中,红色框中的每一块在其时域中仅存在一个源信号有电场分量。 图2 局部优势Fig.2 Local dominance 本文将用一种改进的“两步法”来解决图2所示的BSS模型,该方法的原理框图如图3所示。 图3 两步法框图Fig.3 The framework of ‘two-stage’ 为了简单起见,在下面的讨论中X表示混合信号、S表示源信号、Y表示分离信号。在第一步中,先将混合信号X分块,构造每一块的局部协方差矩阵,然后对每一个局部协方差矩阵进行特征值分解(eigenvalue decomposition, EVD),提取出最大特征值对应的特征向量,最后将每一块提取的特征向量进行聚类,得到混合矩阵。在第二步中,先对分离信号进行初始化,然后将混合信号与估计的混合矩阵进行列式分解,通过循环迭代得到分离信号。本文用密度聚类[22]的方法来完成第一步混合矩阵的估计,再用迭代拉格朗日乘子法[23]来完成第二步源信号的分离,以下章节将给出每一步的详细讲解。 2.2.1 数据预处理 首先利用源信号的非平稳特性引入局部协方差矩阵。将M*L维的混合信号X平均划分为Q个相互独立的子块,每个子块相当于一个M*[L/Q]维的矩阵。定义混合信号第q个子块的局部协方差矩阵为: (3) (4) (5) 对每一块的局部协方差矩阵进行EVD为: (6) 式(6)中,Vq是特征向量矩阵,∑q为特征值矩阵。提取Vq中最大特征值所对应的特征向量为aq,对所有Q个子块进行如上所示的EVD,得到Q个特征向量,组成特征向量矩阵为A=[a1,…,aQ]。 对矩阵A的各列向量进行密度聚类,找出N个簇,将每一簇取均值求得混合矩阵。在(M,N)=(2,3)的情况下,将所有求得的特征向量降维映射到二维空间中,其散点图如图4所示。图中共有3个簇,不同簇被标记成不同的颜色,每一个簇的均值对应估计的混合矩阵每个列向量,不在大密度区域中的点被标记为离群点。 图4 聚类示意图Fig.4 The diagram of the clustering 2.2.2 密度聚类算法 密度聚类算法核心思想是用一个点R邻域内的邻点数量来衡量该点所在空间的密度,将大密度点及周围密度可达的邻点划分为一簇,从而找出形状不规则的簇,且不需要提前输入簇的个数。 下面给出一些基本定义,对于特征向量矩阵A的每一列特征向量a,称之为一个数据点。本算法重点考虑了两个因素,定义密度时的邻域半径R和定义聚类中心点时的最小邻域点数P。 1)R邻域:定义NR(a)={b|d(b,a)≤R}为a的R邻域,d(b,a)表示b与a之间的距离,显然a,b∈A。 2)密度ρ:定义ρ(a)=|NR(a)|为a点的密度,它是依赖于邻域半径R的整数值。 3)聚类中心:若ρ(a)≥P,则称a为聚类中心,由聚类中心构成的集合为AC,ANC为非聚类中心点构成的集合。 4)离群点:若ρ(a) 5)密度直达:若a∈AC,b∈NR(a),则称b是从a出发密度直达的。 6)密度可达:设a1,a2,…,am∈A,m≥2,若ai+1是从ai密度直达的,i=1,2,…,m-1,则am是从a1密度可达的。 密度聚类算法的过程基本描述为:任意满足密度条件的聚类中心点I,数据集中所有从I点密度可达的点O所组成的集合构成了一个完整的簇,接着继续选择另一个聚类中心点去寻找密度可达的数据集,构成另一个簇,直到没有新的点加到任何簇中。根据密度聚类算法估计混合矩阵的具体过程如下: 步骤一:输入2.2.1节中的特征向量矩阵A,设置邻域参数R和P,初始化聚类中心集,簇的个数。对于数据中的每个点,计算其对应的k个最近邻域距离(一般k设置为4),并将数据集中所有点对应的k个最近邻域距离按照降序方式排序,绘制成“K-距离”曲线。R的值一般设定为曲线图拐点位置的值。P值的设定需要满足:P≥dim+1,dim表示数据的维度。例如,在本文算例中R设定为0.03,P设定为3。 步骤二:对于A中任意的a,通过欧式距离的度量方式,找到其R邻域子集NR(a),若子集个数|NR(a)|≥P,则将a加入聚类中心集AC,否则标记a为离群点。 步骤三:若AC=φ,则算法结束,否则转入步骤四。 步骤四:在AC中选择一个聚类中心a,建立新簇K,将a的R邻域子集NR(a)所有的点加入K。并对NR(a)中所有未被处理的点b检查其R邻域子集NR(b),若|NR(b)|≥P,则将NR(b)中未归入任意簇的对象加入簇K。 步骤五:输出N个簇:K1,…,KN,对每一个簇求均值,得到C1,…,CN,则C=[C1,…,CN]为估计的混合矩阵。 本文采用一种基于lp范数最小化的模型来实现源信号的分离,其目标在于根据线性瞬时混合模型式(1)找到Sd的最稀疏项,因此源分离的等效模型可以表示为[23]: (7) 用拉格朗日乘子将式(7)转化为一个新的无约束优化问题: (8) 式(8)中,α∈M为拉格朗日乘子。式(8)进一步展开为: Sd=Ψ-1(Sd)CH(CΨ-1(Sd)CH)-1Xd (9) (10) (11) 本文通过相似度和相对均方根误差(RRMSE)来衡量BSS系统的性能。 相似度是用来衡量两个信号波形之间的相关程度的,表达式为: (12) 相似度的范围是0≤ρi≤1,ρi越大说明分离的效果越好,反之则越差,当ρi=1时表示分离的信号与源信号完全一样,一般来说,相似度大于0.8时则可以认为分离效果较好。 相对均方根误差(RRMSE)用来描述两个信号之间的偏离程度,表达式为: (13) RRMSE越小说明分离的效果越好,分离出的信号数据与原始信号数据之间相差越小,相反的,分离效果越差。 本文算例采用球头锥的模型来模拟真实弹头结构,利用旋转对称体球面等效源区域分解算法(EPA-BOR)[24]得到弹头的回波信号,分别用本文提出的算法和文献[25-26]提出的算法进行混合矩阵估计和源信号的分离。 考虑3个目标两个通道的情况,设目标回波中有3个弹头目标作进动,每个弹头的大小各不相同,弹头质心为目标的中心,弹头目标模型如图5所示。 图5 弹头目标模型Fig.5 The model of the warhead targets 弹头的尺寸和微动参数如表1所列。 表1 目标几何和微动参数Tab.1 Target geometry and fretting parameters 雷达发射采用单频脉冲信号,载频为10GHz,采样频率为500Hz,雷达视线角为70°,观测时间为 4s。一般来说,目标相对于雷达之间的运动有平动和微动两种情况,本文研究的弹头目标只考虑微动情况下的模型,暂时忽略平动的影响,利用EPA-BOR与电磁散射特性分析方法获得3个目标的回波,如图6所示。 图6 三个源信号Fig.6 The three source signals 随机生成的混合矩阵为: (14) 由此,3个源信号经过混合矩阵得到如图7所示的两个混合信号。 图7 两个混合信号Fig.7 The two mixing signals 由于在线性瞬时混合的模型中,混合矩阵是实数矩阵,混合信号的实部包含了有效信息,因此对混合信号的实部首先进行数据预处理再进行密度聚类,得到如图8所示的聚类结果图。图中一共有3个不同的簇,不在大密度区域的点属于离群点,然后对每一个簇求其均值,得到估计的混合矩阵为: 图8 聚类结果Fig.8 The result of the clustering (15) 采用文献[25]中基于时频分析的算法求得的混合矩阵为: (16) 表2为两种方法估计的混合矩阵的相似度和RRMSE,可见本文算法能够更加准确地估出混合矩阵。 表2 混合矩阵的相似度和RRMSETab.2 Similarity and RRMSE of mixing matrix 采用基于lp范数最小化的算法与采用文献[26]中基于压缩感知的算法得到的分离信号与源信号进行对比,结果如图9所示。 图9 分离信号与源信号对比图Fig.9 The contrast diagram of the separated signals and source signals 分别计算两种算法与源信号的相似度和RRMSE,如表3所列。 表3 分离结果表Tab.3 The result table of the separation 结果表明,本文提出的算法得到的分离信号与源信号相似度较高,都达到99%以上,误差也在一定范围中,都在10%以下,与文献[26]得到的分离结果比较,分离性能更加优越。 本文以空中微动群目标的BSS为研究目的,给出了一种基于密度聚类和lp范数最小化相结合的高效分离方法。实验结果表明,本文提出的算法能够有效应用在弹头目标回波的盲分离中。利用该算法估算的混合矩阵精确度高,分离的信号与源信号相比误差较小,在解决一些密度聚类算法中需要事先输入类别个数问题的同时,避免一些源分离最优化算法中出现局部极小值的问题,使分离性能大大提高,更加符合实际场景。当群目标之间距离较近时会存在耦合关系,因此未来的工作重点将解决群目标之间的相互耦合作用,存在耦合的群目标盲分离是一个有意义且具研究价值的问题。本文考虑的是一种理想的场景,未考虑噪声对系统的影响,实际中噪声是不可忽略的,如何在有效去除噪声的情况下达到更好的分离效果是接下来的又一重点工作。1 盲源分离系统模型

2 算法原理
2.1 整体框图

2.2 混合矩阵估计
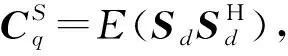

2.3 源信号分离

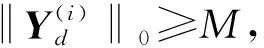


3 仿真分析
3.1 评价标准
3.2 仿真算例







4 结论
