一种用于液相检测的耗散型石英晶体微天平振荡电路设计

缪春海，王 鹢，郭 兴

(兰州空间技术物理研究所 空间环境载荷工程中心，兰州 730000)

0 引言

基于经典Sauerbrey公式，石英晶体微天平(quartz crystal microbalance，QCM)因其低成本、高灵敏度、易于实时监测等优势，既可作为膜厚传感器应用于膜厚检测[1]；又可作为气敏传感器检测目标气体质量，在PM2.5检测[2]、塑料制品或食品中塑化剂气体检测[3]、糖尿病患者的丙酮气体检测[4]、爆炸挥发性气体检测[5]等诸多领域得到广泛应用。但目前QCM的使用需要同时满足气相环境与刚性吸附膜这两个条件，因为液相环境的阻尼远远大于气相环境，不同的溶液环境阻尼大小也不一致，这使得传统QCM在液相中难以稳定工作。同时，阻尼增大导致石英晶体静态电容对谐振频率相位的影响不容忽视。

目前适用于液相环境的QCM振荡电路主要分为普通振荡电路和锁相环振荡电路。普通振荡电路基于自激振荡原理，具有代表性的普通振荡电路有射极耦合振荡电路[6]、桥式振荡电路[7]和平衡桥式振荡电路[8]。这类电路多采用增大电路增益的方法提高起振性能、使用并联电感补偿静态电容，虽然在一定程度上能够使得QCM在液相中稳定起振，但是存在起振性能并不宽泛、静态电容补偿不完善等问题，对测量结果存在较大影响。锁相环振荡电路利用石英晶体的电抗特性，将晶体锁定在纯阻性的状态下，控制石英晶体发生串联谐振[9-10]。该类型电路具有较好的起振性能，但是依然需要对静态电容进行补偿。

液相中QCM获取得到的谐振频率f并不只与吸附膜质量有关，还受吸附膜与溶液力学性质的影响[11]，因此谐振频率f不能准确描述吸附质量。Rodahl等人提出了耗散因子D的概念，其与溶液的密度、黏性等性质有关，与谐振频率f一同能够相对完整地描述溶液密度、黏度、吸附膜质量、剪切模量等物理参数。

本文结合普通振荡电路与耗散因子，设计出适用于液相环境下，能够同时获取谐振频率与耗散因子的耗散型石英晶体微天平(QCM-D)振荡电路。利用自动增益控制技术解决液相环境阻尼过大的难题，并且能显著提升起振性能；经过理论分析提出使用并联电容补偿技术，有效避免静态电容对谐振频率相位的影响；最后对振荡电路进行实验测试以验证性能。

1 QCM-D工作原理

根据经典Sauerbrey公式，当气相环境中石英晶体表面附着一层刚性薄膜时，石英晶体谐振频率的变化量Δf与附着物质质量的变化量Δm存在线性关系：

(1)

其中，f0表示石英晶体的谐振频率，μq、ρq分别为石英晶体的剪切模量、密度。因此基于Sauerbrey公式原理的QCM主要应用于气相环境下微质量的检测，如月尘测量[12]、膜厚检测。

1985年Kanazawa和Gordon推导出了Kanazawa-Gordon公式[13]，当石英晶体工作于牛顿流体中时，谐振频率的变化量Δf与牛顿流体的密度ρl和黏度ηl存在一定的关系，如式(2)所示：

(2)

耗散因子D的概念由Rodahl等在1996年提出，它表示石英晶体在一个振荡周期内消耗能量与储存能量的比例[14]，如式(3)所示：

(3)

根据Kanazaw和Rodahl建立的力学模型[15]，当石英晶体表面有一层吸附薄膜，并且薄膜上方有一厚度可视为无穷大的液体时，ρf、hf、μf、ηf分别表示膜的密度、厚度、剪切模量和黏度，ρq、hq分别表示石英晶体的密度和厚度，ρl、hl、μl分别表示液体的密度、厚度和剪切模量，如式(4)、式(5)所示：

(4)

(5)

获取耗散因子D的方法由Rodahl和Hook等[18-20]提出，石英晶体当进入稳定振荡状态后与振荡电路断开，开始进行衰减振荡，其波形满足：

u=Ae(-t/τ)sin(2πft)

(6)

τ为时间常数，f为谐振频率。耗散因子D为：

(7)

耗散因子D与气/液相下吸附物质的黏性、质量、吸附膜的剪切模量等存在一定的关系，通过耗散因子D的测量能够得出这些信息。

2 QCM-D振荡电路设计

如图1所示，QCM-D基本结构为液体池、石英晶体传感器、振荡电路、数据采集电路、模拟开关、FPGA控制模块与上位机。待测溶液导入液体池，与液体池中的石英晶体传感器的工作面电极接触；振荡电路激励石英晶体传感器使其稳定振荡；模拟开关控制石英晶体与振荡电路断开、与数据采集电路连接，数据采集电路再将模拟信号转化为数字信号，最后传输给上位机；上位机对原始数据存储后进行处理，显示最终的测量结果。QCM-D振荡电路原理图如图 2所示，本文基于自激振荡原理、结合耗散因子D设计出QCM-D的振荡电路部分，针对液相中QCM-D难以起振的问题进行深入分析，再选择合适的方案进行解决。

图1 QCM-D基本结构Fig.1 Basic structure of QCM-D

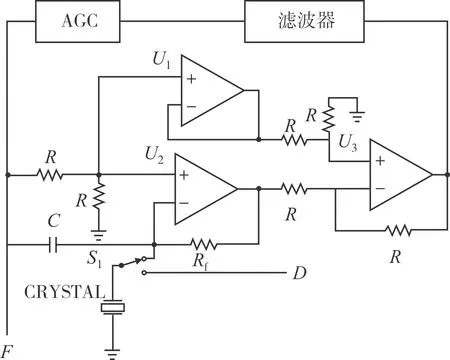
图2 QCM-D振荡电路原理图Fig.2 Schematic diagram of QCM-D oscillation circuit

2.1 静态电容的补偿

石英晶体等效电路模型如图3所示，该模型中石英晶体包含两条支路：一条是静态支路，只包括静态电容C0，静态电容C0是晶体两个电极平板电容、引线与夹具分布电容和驱动电路输入电容等归纳而成的一个与动态支路并联的电容；另一条是动态支路，包括Rm、Cm和Lm，Rm受到机械摩擦和石英晶体所处环境阻尼的损耗的影响。

图3 石英晶体的Butterworth-Van Dy (BVD) 电路模型Fig.3 Butterworth-Van Dy (BVD) circuit model of quartz crystal

石英晶体动态支路的导纳Gm如式(8)所列：

(8)

Gm的实部和虚部分别如式(9)、式(10)所列：

(9)

(10)

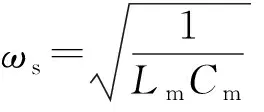
此时考虑静态支路的影响，石英晶体的实际导纳G如式(11)所列：

(11)

G0为静态支路的导纳，G的相位可表示为：

φ=arctan(ωsC0Rm)

(12)

由式(12)可以看出，静态电容C0对相位的影响随着Rm的增大而增大，这使得串联谐振频率ωs的相位不为零，且出现的相位偏移越大。如图4所示，一般静态电容C0在20pF左右，这里选取C0=20pF。石英晶体在空气中等效阻抗Rm大概为几十Ω，当谐振频率为10MHz时，φ仅有几度，石英晶体因静态电容C0带来的相位偏移很小，几乎没有影响，因而在空气中石英晶体容易起振；在液相中Rm可达到几百甚至上千Ω，当Rm为500Ω时，φ超过了30°，相位偏移较大，使得振荡电路不满足相位平衡条件，难以起振，对于更高频率30MHz，静态电容C0引起的相位偏移也更多。为了液相环境中的QCM-D振荡电路满足相位平衡条件，需要采取措施去除电路中晶体并联电容的影响。

图4 C0=20pF时，φ与Rm的关系Fig.4 When C0=20pF, the relationship between the φ and the Rm

如图5所示，在电路中添加一电容C，在A点使用基尔霍夫电流定律。

图5 电容补偿电路Fig.5 Capacitance compensation circuit

如式(13)所列：

(13)

(14)

(15)

此时C0被补偿后U2的相位在晶体的串联谐振频率点时为0，根据相位平衡条件，振荡电路的其他部分相位也需要为零。因此，调整C=C0后，在任何频率下C0都可以得到补偿。

(16)

此时电路增益只与Rm有关，石英晶体稳定控制着电路的谐振频率。

2.2 自动增益控制驱动

如图6所示，在输出与输入之间加入一自动增益控制放大器AGC，实际工作中Rm的值变化范围很大，导致Uo变化较大，AGC能输出几乎恒定的电平幅值，满足振荡电路幅度平衡的要求。该AGC的选择要求为：一方面为实现较好的起振性能需要很宽的动态范围；另一方面，需要较大的带宽且在晶体谐振频率处的相移为180°的整数倍，以满足相位平衡条件。

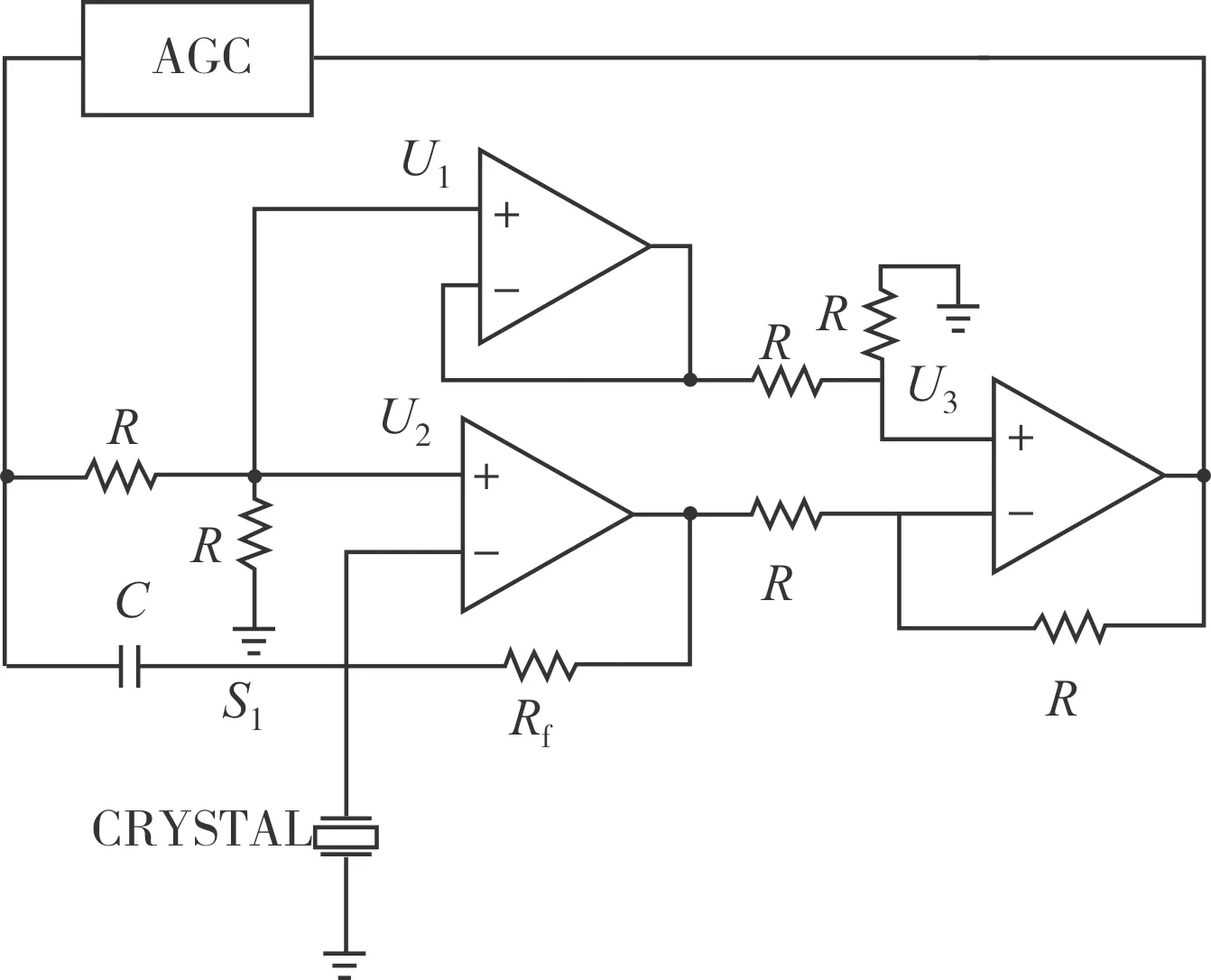
图6 自动增益控制振荡电路Fig.6 Automatic gain control oscillator circuit

2.3 带通滤波器设计

本文设计的QCM-D振荡电路采用基频为10MHz的石英晶体传感器，振荡频率采用10MHz，为滤除不需要的高次谐波，需要设计带通滤波器。贝塞尔滤波器在通带内延时特性最为平坦，但也存在截至特性较差的缺点。然而，由于在高次谐波点处引入了较大的相移，使得电路无法在这些频率点振荡。所以本文采用三阶贝塞尔带通滤波器，如图7所示。在根据三阶贝塞尔带通滤波器计算公式得出本文所需的滤波器后，经由实际电路调试与测试结果，对滤波器元件值进行合理调整。

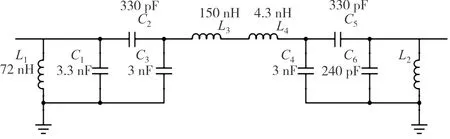
图7 三阶贝塞尔带通滤波器Fig.7 Third-order bessel bandpass filter

2.4 耗散因子D的获取

由式(6)、式(7)可知，为获取石英晶体的耗散因子D：首先需要将石英晶体与QCM-D振荡电路连接，石英晶体起振；稳定振荡后，石英晶体与QCM-D振荡电路断开，石英晶体进入衰减振荡状态；获取石英晶体两端的电压信号，再通过式(6)得出τ值与谐振频率f，由式(7)最终计算得出耗散因子D的值。因此，如图 2所示，加入一高速开关S1。

石英晶体在空气中衰减振荡的时间大概为十几ms，在液体中为几百μs，因此，高速开关的导通时间应在1μs之内，减小导通时间对波形的影响。其次，高速开关在导通时存在导通电容与电阻，当容值与阻值较大时，静态电容无法被补偿，因此需要导通电容与电阻值尽可能小。

3 QCM-D性能测试

如图8所示，为本文设计的QCM-D振荡电路实物图。为验证该QCM-D振荡电路的性能，室温23℃下，将石英晶体激励电极滴入纯水，每隔10s采集QCM-D的输出频率，获得QCM-D在6000s内频率的变化情况。如图9所示，在6000s内石英晶体的频率漂移在7Hz以内，实验表明该QCM-D具有良好的频率稳定性。同时，测得石英晶体在水中的衰减时间τ为121.5μs，根据式(7)可得水中的耗散因子D为2.636×10-4。

图8 QCM-D振荡电路实物图Fig.8 QCM-D oscillator circuit diagram

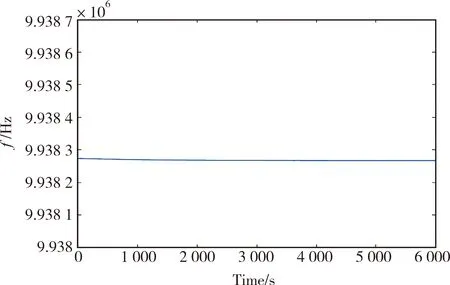
图9 水中的频率稳定性Fig.9 Frequency stability in water

4 结论

本文设计的耗散型石英晶体微天平QCM-D，通过采用自动增益控制放大器AGC解决液相环境阻尼大难以起振的问题，实现较宽范围的起振性能，并通过手动调整并联电容大小的方式补偿石英晶体静态电容，使得QCM-D能够真正工作在串联谐振频率上，该QCM-D能稳定工作于80%浓度丙三醇溶液。对比仅适用于气相环境刚性薄膜的普通QCM，QCM-D具有普通QCM功能的同时，还适用于液相环境与粘弹性薄膜中，通过获取耗散因子D能反映溶液的黏度、薄膜的质量、剪切模量等物理参数，且保持体积小巧、便捷性强、成本低廉的特点，易于推广，适用于诸多领域，存在广阔的应用前景。