适用于信标光检测的非对称中值滤波改进算法
2022-08-09徐勤健
徐勤健,王 永,贾 蕴
(山东航天电子技术研究所,烟台 264003)
0 引言
星间激光通信作为新型的通信方式,具有大带宽、高速率等优越性能。激光通信系统中的捕获、跟踪、瞄准是由短波红外相机的位置来确定的,因此光斑位置的准确性会直接影响激光通信系统的精度。然而在红外系统实际工作环境中会受到干扰,使图像产生模糊、噪声等。因此需要在光斑定位前进行滤波处理。在空间域的范围内,对噪声的滤波又可以分为线性和非线性[1]。对于椒盐噪声[2]来说,非线性滤波中的中值滤波效果较好且应用广。
为了提高中值滤波算法效率,马运强等[3]提出了利用邻窗的相关性,保留原排序的同时分别迁入迁出新数据,简化算法的方法,来提高运算速度;赵亮等[4]在FPGA中,通过FIFO和寄存器进行窗口变换,进行并行运算,达到快速滤波的目的;董恩增等[5]选择5×5滤波窗口的基础上,采用行列以及对角的像素值,进行归并插入排序,可满足运算实时性的要求。Cao等[6]在信号统计的基础上对中值滤波的影响进行分析。Chen等[7]提出基于差分域的中值滤波检测。除此之外,还有很多学者提出了不同的改进中值滤波算法[8-12],都有着各自的优势和不足。
针对3×3滤波窗口处理速度较慢的问题,本文提出了一种改进的快速中值滤波算法,该算法可以在尽量保证原有3×3窗口的滤波效果条件下,提高计算速度。
1 红外图像盲元、噪声与团簇
利用红外成像系统得到的图像具有一定的噪声和非目标物体的背景干扰。这些噪声会使得红外图像质量下降,造成斑形状不规则、背景混乱、目标不清晰等后果。盲元[13]表现为短波红外探测器成像图像中的过亮或者过暗的噪点。过热像元定义为像元噪声电压大于平均噪声电压 10倍的像元。死像元定义为像素响应率小于平均响应率10%的像元。坏点定义为在50%的均匀光照下,响应偏差超过均值±25%的像元点。团簇是指连在一起的坏像元。
根据使用手册可知,某公司的短波红外探测器等级划分标准如表1所列:
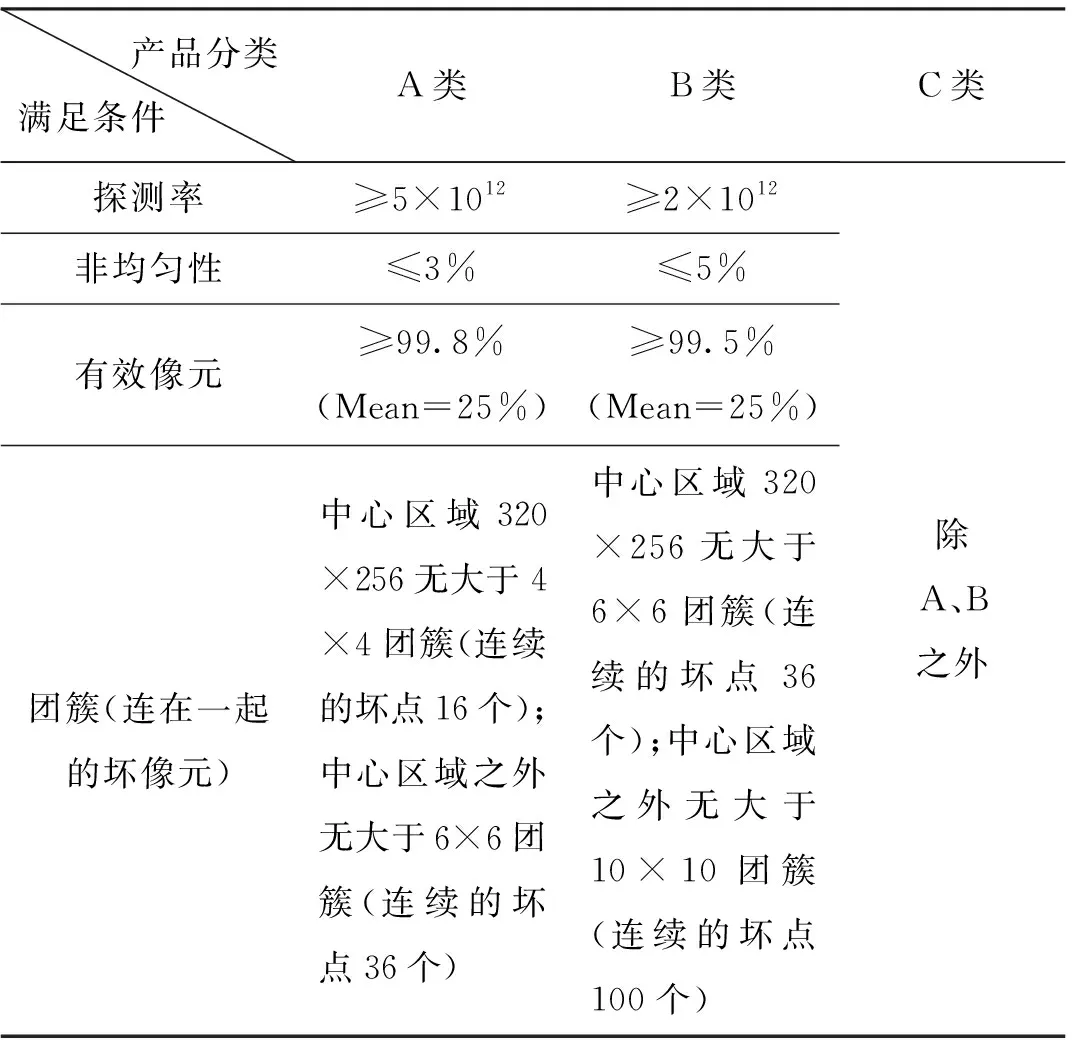
表1 短波红外探测器等级划分标准Tab.1 Standard for classification of short wave infrared detectors
本次选用的某公司的InGaAs短波红外探测器为B类。由表1中数据可知,对于320×256的图像,B类探测器中心区域无大于6×6的团簇,中心区域之外无大于10×10的团簇。现利用短波红外焦平面探测器,得到分辨率为640×512的图像,截取某单点盲元位置和某个团簇区域,如图1所示。

图1 截取某单点盲元位置和某个团簇区域Fig.1 Intercept the location of a single point of blind pixel and a blind pixel cluster
盲元补偿[14]又称为盲元校正,首先利用盲元检测方法标记出位置,之后在盲元所在的位置,利用盲元周围的有效信息对其进行修正。补偿方法有很多,常见的有中值滤波法、邻域线性插值法和相邻元替换法。线性插值法原理如下:
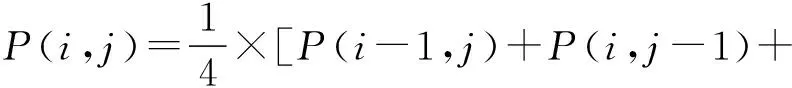
(1)
线性插值法计算简单,但对于盲元和噪声较多的图像,补偿效果欠佳。对红外图像的盲元与团簇进行滤波处理,可以有效提高图像质量,有利于提高下一步的光斑定位研究的准确度。
观察红外成像原图像,大部分盲元点为单点,若采用中值滤波进行图像处理,对于盲元点滤波效果佳。对原图进行3×3模板的中值滤波,图2为图1(b)位置团簇位置滤波后的效果图。

图2 截取团簇位置滤波效果图Fig.2 Filtering effect of cluster position
分析图1(b)可知,该团簇区域连续坏点为10个,对于团簇区域,观察图2位置,中值滤波也可以得到较好的滤除效果。
2 改进的快速中值滤波算法
2.1 传统中值滤波算法
中值滤波[15]的原理是在窗口范围内,将图像内的像素点的灰度值按照一定顺序将数据进行排序,并选择中间值作为该窗口的输出值。这种方法本质上是排序统计。由于其特性是取中间值,因此对随机的孤点噪声的效果较好。
对于椒盐噪声而言,中值滤波的滤波效果较好。一般来说,对于同一图像,窗口越大滤波效果越好。然而窗口增大会使硬件平台搭建时占用资源较多,且耗时大。因此,选择合适的窗口大小对于整个图像处理过程而言较为重要。
2.2 非对称中值滤波算法
对于光斑图像而言,3×3窗口的经典滤波算法对盲元、噪声和团簇的滤除效果较好。但在进行滤波的过程中,同一像元重复参与计算次数较多,计算速度较慢。因此,本文提出一种非对称快速中值滤波算法。如图3所示,坏点1 (i,j)和坏点2 (i+1,j)为待处理的像素,改进的中值滤波算法执行的步骤为:
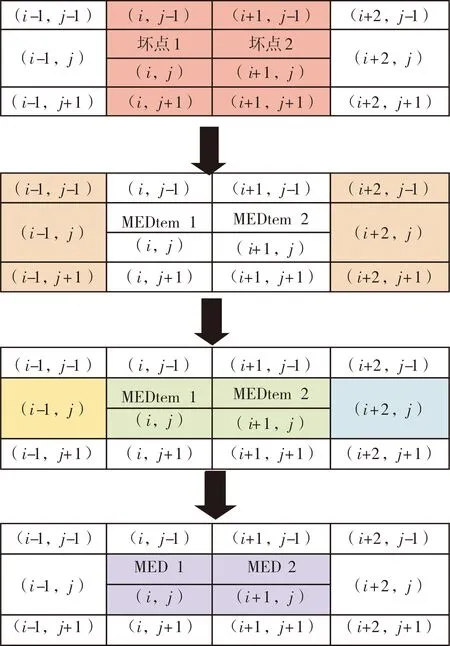
图3 改进的快速中值滤波Fig.3 Improved fast median filter
1)取窗口大小为3×4,坏点1 (i,j)和坏点2 (i+1,j)为待处理的像素,周围其余10个像素为(i-1,j-1)、(i,j-1)、(i+1,j-1)、(i+2,j-1)、(i-1,j)、(i+2,j)、(i-1,j+1)、(i,j+1)、(i+1,j+1)、(i+2,j+1);
2)对于坏点1和坏点2,首先对(i,j-1)、(i,j)、(i,j+1)、(i+1,j-1)、(i+1,j)、(i+1,j+1)6个像素值按大小进行升序排列,取6个值中的中间两个值记为MEDtem1和MEDtem2;
3)对窗口内最左列3个像素值(i-1,j-1)、(i-1,j)和(i-1,j+1)进行升序排列,最右列同理;
4)将步骤2)中得到的中值MEDtem1和MEDtem2与最左列中值(i-1,j)比较,得到中值MED1,同理将MEDtem1和MEDtem2与最右列中值(i+2,j)比较得到中值MED2;
5)将MED1和MED2替换掉待处理的坏点1和坏点2,完成滤波。
算法流程图如图4所示。
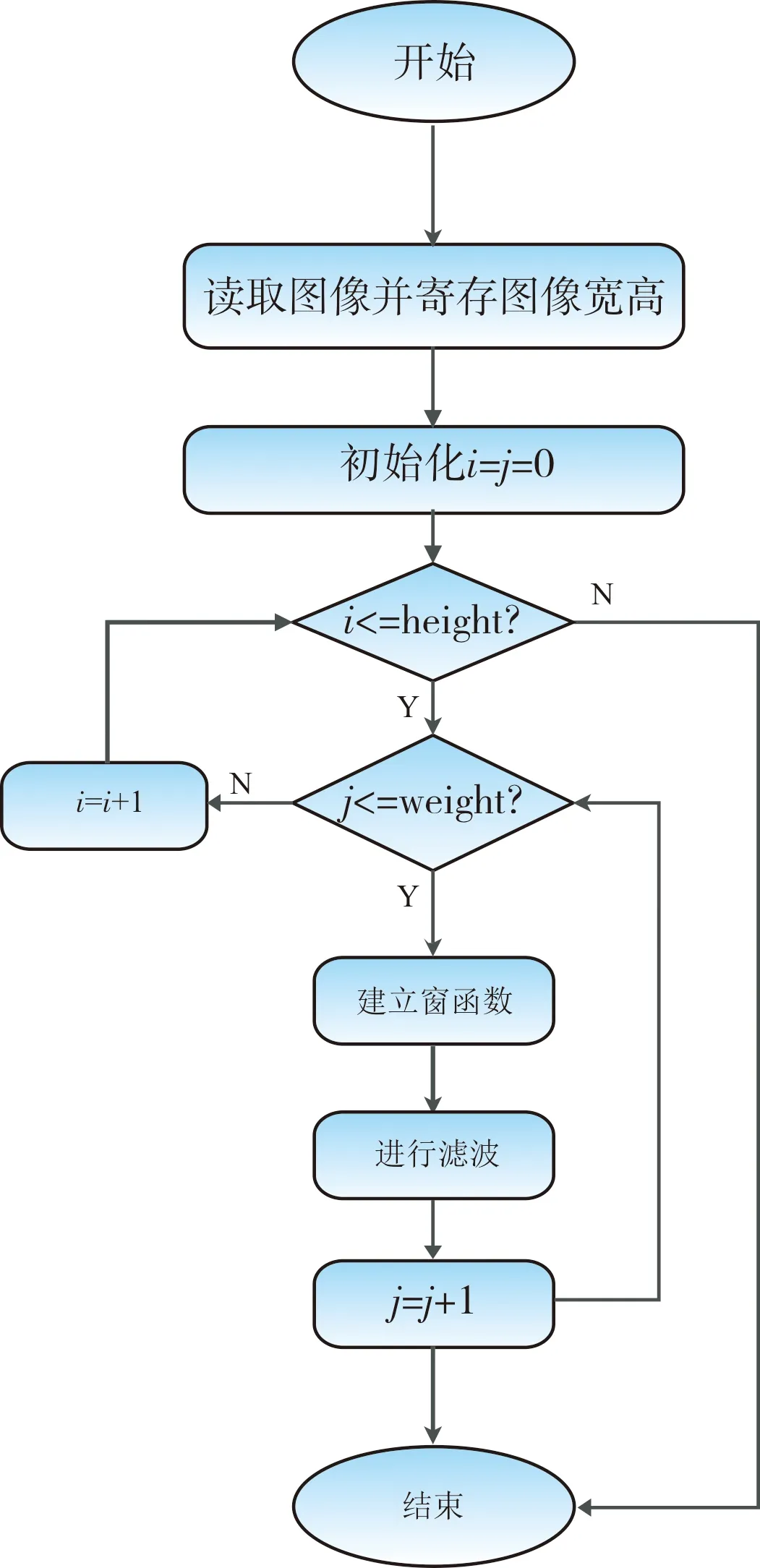
图4 滤波流程图Fig.4 Filtering flowchart
3 经典算法与改进算法计算量对比分析
计算机在进行多数据排序时,可供选择的方法较多。因此需要根据不同的应用环境来进行具体排序方法的选择。现输入一个长度为n的行向量矩阵:
a=[a1,a2,a3,…,an]
(2)
选择一种排序方法,对原行向量的数据进行重新排序:
b=[a11,a21,a31,…,an1]
(3)
使得:
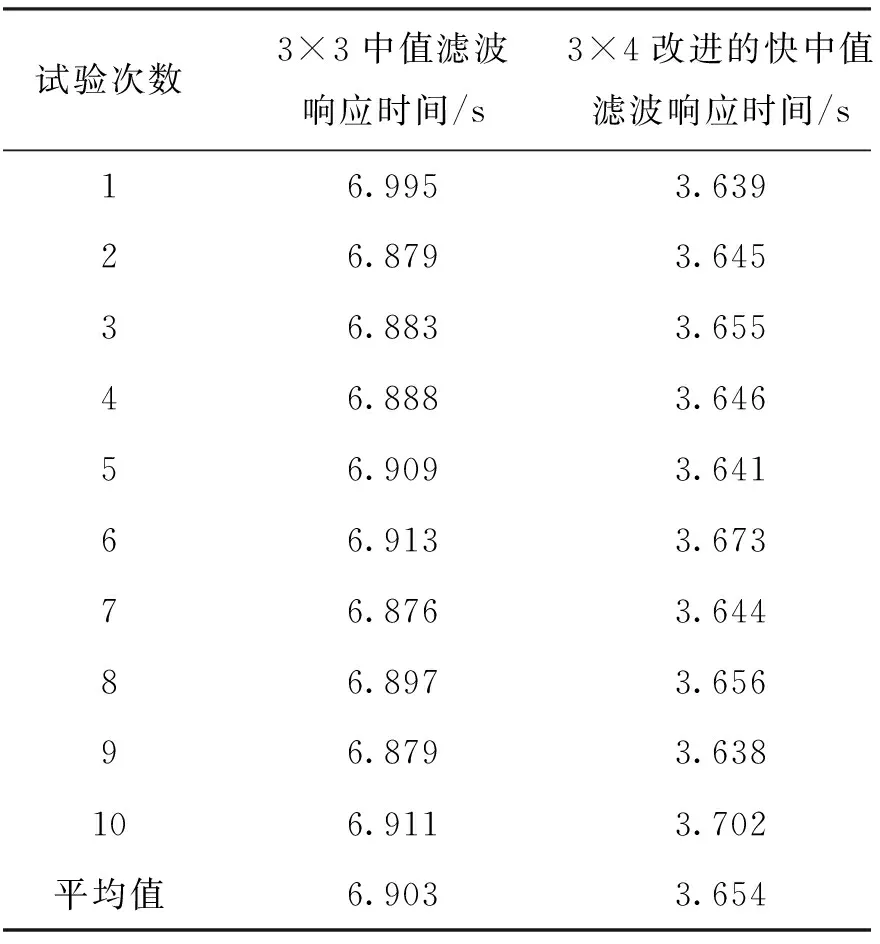
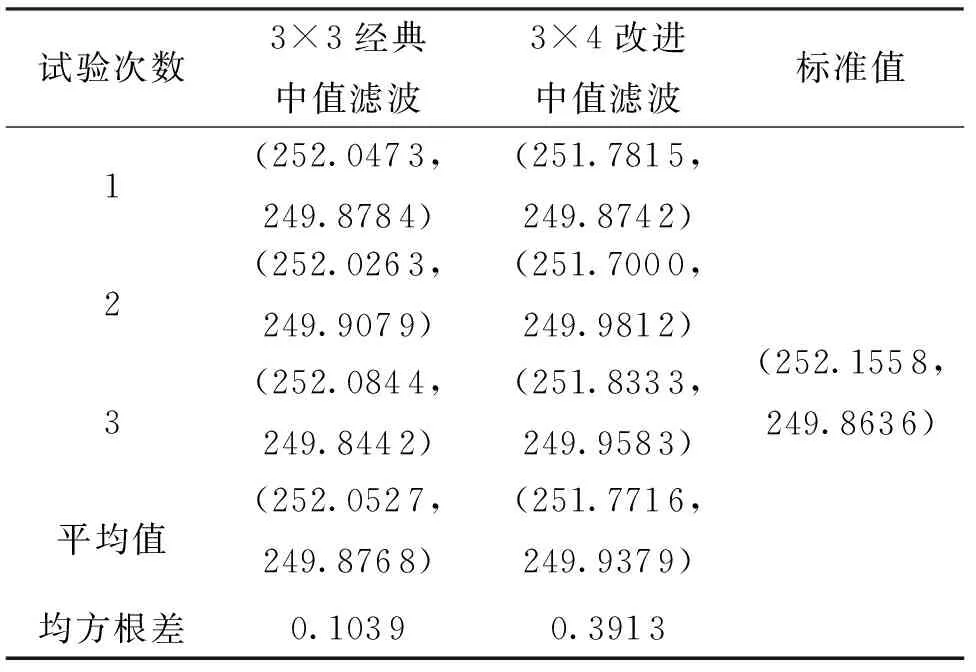
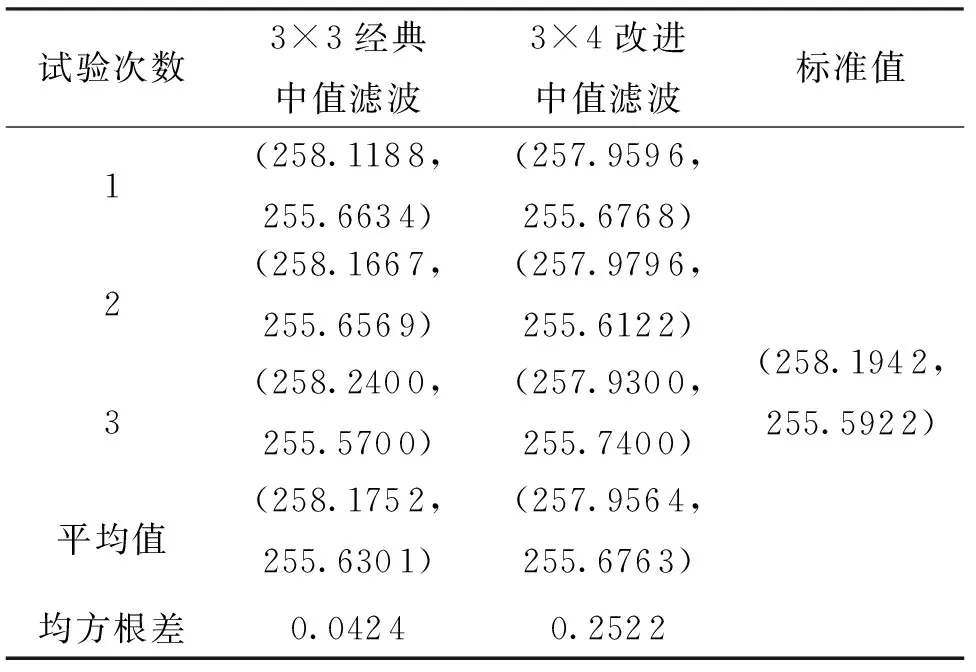
a11 (4) 为统一计算量的衡量标准,本文选用冒泡法[16]进行排序,以进一步对计算量以及程序运行时间进行比较。 冒泡法的原理[17]为:在1组数据中,每2个数据进行大小比较,若前者大于后者,则2者交换顺序,否则保持位置不动。在第1组数据比较完成之后,进行下1组比较,直至最后1组中最后1个比较完成。 考虑到探测器所得红外图像不仅存在盲元问题,还存在噪声干扰等,因此对图像计算量统计时,选用的是整个图像像素值,而非仅仅考虑盲元位置。对于3×3窗口的中值滤波而言,一个窗口内的比较次数为9个数值间每两个数值进行比较后决定是否交换位置,一个窗口内的中值滤波结果值替换掉窗口中心1个位置的像素值,因此计算量nc为: (5) 对于m×n大小的图像而言,比较次数Nm×n为: Nm×n=nc×(m-2)×(n-2) (6) 对于改进的3×4窗口的滤波算法来说,一个窗口内的中值滤波结果值替换掉窗口中心两个位置的像素值,计算量np为: (7) 对于m×n大小的图像而言,由于现存的探测器输出图像的横纵坐标均为偶数,因此默认m为偶数,比较次数Nm×n为: (8) 本次使用探测器为某公司InGaAs短波红外探测器,试验所得原图像分辨率为640×512,像元尺寸为15μm×15μm,像素可操作率大于99.5%,由观测实际输出原图像可知,盲元数量小于100。 采用MATLAB R2013b对实测的图像进行仿真分析。现对光斑图像进行加噪得图,并使用经典3×3窗口中值滤波和改进的3×4快速中值滤波对加噪后的图像进行处理。为了便于展示,将原图像进行截取,截取矩形大小为180×120,左上角坐标值为(230,194),结果如图5所示。 图5 光斑滤波效果图Fig.5 Effect of spot filtering 通过图5观察可知,非对称中值滤波改进算法与3×3窗口的中值滤波算法去噪效果相当。 对于m×n大小的图像,初始化为: m=16 分别对m和n进行自增16,直至到达1024。通过程序仿真观察其计算量变化,结果如图6所示,上平面为3×3矩阵自0增加至1 024的计算量变化平面,下平面为3×4矩阵自0增加至1024的计算量变化平面,二者均随m、n值的增加而增加,且差值逐渐增大。 图6 不同滤波算法计算量比较Fig.6 Comparison of calculation amount of different filtering algorithms 对于使用某公司InGaAs短波红外探测器,试验所得的640×512大小的图像进行处理,多次运行程序得到响应时间如表2所列。 表2 不同滤波方法响应时间对比表Tab.2 Comparison table of response time of different filtering methods 下面考虑不同的滤波对后续光斑定位结果的影响。首先构建一个标准高斯光斑,图像大小为500×500,高斯光斑大小为22×22,截取图中间部分如图7所示。 图7 标准高斯光斑中间部分截图Fig.7 Screenshot of the middle part of standard Gaussian spot 首先计算原图形心作为标准值,将原图加入密度为0.02的椒盐噪声,分别在两种滤波条件下计算光斑中心位置,进行30次试验,记录部分结果如表3所列。 表3 标准高斯光斑定位仿真结果Tab.3 Simulation results of standard Gaussian spot location 现取实际环境条件下所得不规则光斑形状,图片大小为500×500,光斑大小约为15×13,截取中心部分如图8所示。 图8 实测光斑中间部分截图Fig.8 Screenshot of the middle part of the measured spot 重复上述步骤,进行30次试验,记录部分结果如表4所列。 表4 实测光斑定位仿真结果Tab.4 Simulation results of spot location measured 由表3和表4结果分析可知,3×3经典中值滤波误差较小。考虑改进算法窗口的非对称性,3×4改进中值滤波的Y轴计算误差较小,但X轴有固定的误差,在当前光斑大小的前提下,约为0.38。进行多次随机噪声试验,分别用经典滤波算法与改进算法进行误差分析对比,结果如图9(a)、图9(b)所示。在实际工程应用中,需要结合光路的一致性进行统一标校,可以弥补3×4改进中值滤波带来的X轴计算误差,如图9(c)所示。 由图9分析可知,通过对X轴的坐标标校之后,3×4改进中值滤波的算法仍有一定误差,但误差在可接受范围内。在当前光斑大小的前提下,X轴的固定误差约为0.38。在进行空间激光通信时,光学系统指标恒定,光斑大小不变,因此可以认为标校误差为固定值。若有特殊情况导致光斑大小变化,则需要进行重新标校。 图9 坐标误差与校正Fig.9 Coordinate error and correction 综上所述,在算法计算误差角度看,3×4窗口的改进中值滤波带来的计算误差可以通过统一标校来弥补,误差在可接受范围内。在算法的复杂度角度看,改进的算法既减少了重复操作的次数,又降低了比较次数。对于640×512大小的图像而言,原3×3中值滤波需要进行11713680次比较,改进算法需要4392630次比较,为前者的0.375倍。通过表2响应时间结果数据可知,经典算法响应时间均值为6.903s,改进的快速中值滤波算法响应时间为3.654s,为前者的0.529倍。 本文提出了一种非对称中值滤波改进算法,在原先3×3窗口的中值滤波基础上进行改进。3×3窗口的中值滤波算法滤除效果较好,但是在该算法中同一像元会重复参与计算次数较多,计算速度较慢。本文提出的改进方法首先构建3×4大小的窗口,利用原有3×3窗口在进行两次相邻操作时重复利用的6个像素进行像素值大小排序,利用排序结果中值分别与最左列及最右列中值进行比较,得到结果替换掉中间两个盲元原有的像素值。 从目测角度看,3×3中值滤波与改进的快速中值滤波法滤波效果相当。在算法计算误差角度看,3×4窗口的改进中值滤波带来的计算误差可以通过统一标校来弥补,误差在可接受范围内。但从计算量来看,对于使用某公司InGaAs短波红外探测器,试验所得的640×512大小的图像而言,原3×3中值滤波需要进行11713680次比较,改进算法需要4392630次比较,为前者的0.375倍。经程序仿真,经典算法响应时间均值为6.903s,改进的快速中值滤波算法响应时间为3.654s,为前者的0.529倍。因此,本文提出的改进算法增强了算法的实时性,更适合基于FPGA平台的设计与实现。4 程序仿真结果及分析

n=16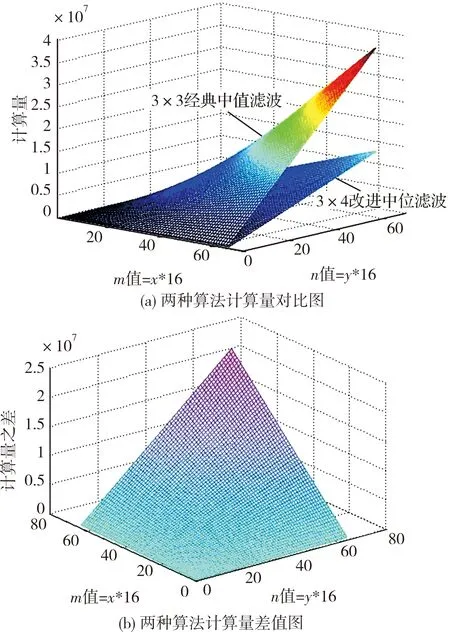



5 结论
