基于深度网络的太赫兹波束预判方法研究

白浪涛，朱忠博，李小军

(中国空间技术研究院西安分院，西安 710000)

0 引言

太赫兹(Terahertz,1THz=1010Hz)波通常指频率在0.1～10THz波段范围内的电磁波，它介于微波与红外光之间的特殊位置，因此具有特殊的物理属性，其在生物医学、6G通信、雷达等诸多领域[1]具有广阔的市场前景。由于太赫兹技术所具有的大容量、高速率优点及其大气特性[2]与星间链路通信场景的特点相匹配，该技术目前已成为星间通信领域研究的聚焦点之一[3]。但是目前报道的太赫兹通信系统都是静态节点的点对点通信，由于空间飞行器自身的运动以及地球轨道的摄动影响，使得空间通信信道为非平稳信道，故目前静态节点的点对点通信系统无法适用于空间通信，在未来应用中，存在许多需要克服的问题，太赫兹波束控制便是其中之一。由于太赫兹波的波束较窄，卫星间通信距离较远，加之机械伺服天线机构负载大、转动惯量大，在采用传统的被动跟踪方式时，在链路噪声及波动误差的影响下，易造成捕获跟踪性能无法达到空间太赫兹通信要求的情况，故需要提前获知下一时刻所需指向角度，提前调整指向机构(即超前瞄)，使之克服轨道摄动力影响所带来的角度误差，以实现太赫兹星间高速通信。

目前，国内外主要通过外推经典力学模型对卫星轨道进行预报[4]，并通过上注导航星历上传至卫星，卫星通过坐标转换调整指向以达到星间通信，由于轨道预报精度受到任务要求、定轨精度、轨道高度及空间动态环境等因素的影响，导致动力学轨道外推的预报精度误差较大。随着神经网络的发展，近年来出现了一些利用神经网络进行轨道预报的相关研究。文献[5]利用BP神经网络作为建模工具，对卫星的轨道位置与速度进行预测，然而由于将卫星位置直接作为神经网络的输出，导致网络状态量动态范围大，限制了预报精度的提高；文献[6]利用长短时记忆神经网络与卷积神经网络相结合对卫星轨道的TLE数据进行预报，在一定程度上提高了中长期预报精度，但该方法针对特定的卫星位置有效，不具有普适性。

文章针对高低轨卫星太赫兹通信应用场景，利用长短时记忆网络(long short-term memory networks,LSTM)建立预测模型，并通过改进粒子群算法(particle swarm optimization, PSO)对预测模型参数进行优化，通过对历史时刻指向误差的分析，掌握其变化规律，再预测未来时刻方位角与俯仰角误差并修正，达到提高链路余量的目的。文中首先对高轨对低轨卫星指向误差特征进行详细分析，利用这些特征制定了一种基于PSO-LSTM深度网络的太赫兹波束预判方法，实时预测下一时刻的指向误差并修正，并对特定应用场景进行仿真分析。

1 指向误差特征分析

由于星间通信存在摄动力影响，卫星轨道模型并非理想的开普勒运动模型，误差矢量始终存在，本文旨在通过分析误差数据从而预估下一时刻所需修正量，提前控制天线机构调整指向角，故在对指向误差矢量分析时，重点在于误差数据为未来预测的影响。通过对摄动力、轨道外推模型的研究，可以发现误差矢量主要取决本体星与目标星的位置与速度，其次外推时间也对误差矢量有影响。因此有必要对误差矢量关于时间和卫星位置的关系特征进行分析，主要讨论方位、俯仰角误差随时间的变化以及外推初始时刻对误差大小的影响。

文章通过STK软件选用BEIDOU-3与IRIDIUM-16仿真搭建高轨对低轨通信场景，通过选择不同的轨道外推模型得到两组卫星之间的位置误差，并通过坐标转换算法将误差矢量转换到实际GEO的本体坐标系中，图1(a)～图1(d)表示了方位、俯仰角误差和距离误差随时间变化的趋势。由图1(a)、图1(b)可知在65d的外推弧段内，误差呈周期性变化，周期约为36d；方位角误差在[-12°,12°]之间，俯仰角误差在[-11°,11°]之间。在1d的外推弧段内，误差呈周期性发散变化，周期约为4 200 s。以2021年1月1日至2021年5月4日的零点作为初始时刻，在卫星参数不变的情况下分别进行外推40d，从图1(e)、图1(f)可以看出，虽然选择同一卫星参数，在同一动力学模型下，由于各种原因不同初始时刻下的误差数据各不相同，40d的方位、俯仰角误差最大值约为[10°,20°]；不过误差大小随初始时刻的分布还是有一定规律的，通过图像可以大致确定这种分布具有一定的连续性、周期性：相邻初始时刻之间关系比较确定，间隔一定时间误差最大值大小相近，经过观察，初始时刻相差14.5d左右时，误差大小最为接近。综上所述，高轨对低轨卫星的波束指向误差数据具有一定的周期性与连续性，故可以采用长短时记忆网络以14d为周期进行序列预测。

图1 指向误差特征曲线Fig.1 Pointing error characteristic curve

2 改进PSO-LSTM预测模型

2.1 长短时记忆神经网络

长短时记忆神经网络是对循环网络进行改进后的深度网络，它有效地回避了循环网络存在梯度消失或梯度爆炸的问题，LSTM网络能够长期记忆信息的关键就是引入输入门(input gate)、输出门(output gate)、遗忘门(forget gate)三个门结构[7]对单元状态c进行管理控制。LSTM主要算法过程为：

ft=σ(Wf·[st-1,xt]+bf)

(1)

it=σ(Wi·[st-1,xt]+bi)

(2)

(3)

ot=σ(Wo·[st-1,xt]+bo)

(4)

st=ot*tanh(ct)

(5)

2.2 改进的粒子群算法

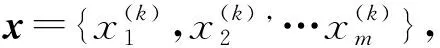
(6)

(7)

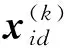
故本文提出由大变小，呈非线性变化的惯性权重ω计算公式，在迭代初期，全局收敛能力较好，提高收敛速度；迭代的后期，适当减小ω，提高算法的局部收敛能力[9]，从而提高算法的精确度。ω的形式如式(8)所示：

(8)

式中，k为当前迭代次数，kmax为算法迭代次数的最大值，η为曲率调节参数，a、b为调节参数，控制ω幅值范围。ω随着k与η的增大由逐渐增大到逐渐减小，为了使迭代周期内ω变化比较平缓，确定使ω(k≈30)=max[ω(k,η)]的η，经过计算可得η=1.74。

2.3 改进PSO-LSTM预测算法流程

改进PSO-LSTM预测模型中关键的参数包含LSTM网络的隐含层层数、隐含层神经元个数和学习率。通过改进的PSO算法对这3项重要参数不断进行优化，以达到最优预测性能。该算法关键步骤如下：

1)初始化参数。设置PSO最大迭代次数、种群数、学习因子、曲率调节参数、定义区间和LSTM网络初始参数。

2)构建LSTM网络预测模型。对训练集样本进行归一化处理，随机初始化粒子位置和速度。

3)确定粒子适应度值。在步骤2)中得到初始LSTM网络参数，对多组14d为周期的指向误差训练集序列数据进行学习并得到预测集，验证集为14d后0.05s时刻的实际指向误差值，将预测集拟合误差的均方根误差作为适应度值。

4)更新粒子群状态。规定粒子与种群当前时刻的最优位置，并根据式(6)、式(7)、式(8)更新粒子位置与速度，计算粒子群适应度值，并保留更好的粒子状态。

5)重复执行步骤3)、步骤4)，判断是否达到终止条件，当满足终止条件时，跳出循环，得到一组最优粒子群状态。

6)使用最优粒子群状态设置LSTM网络参数并进行预测，网络的输出即为模型的预测值。本文所述网络模型流程图如图2所示。

图2 网络模型流程图Fig.2 The flow chart of the network model

3 实例分析

文章选用BEIDOU-3与IRIDIUM-16仿真搭建GEO-LEO通信场景，以2021年1月1日至1月30日作为运行周期，对运行周期1d内进行采样，采样周期0.05s，其中90%用于训练集，10%用于验证集，BEIDOU-3与IRIDIUM-16卫星每0.05s在J2000坐标系下的位置速度信息作为训练集输入，下一时刻的方位、俯仰、距离误差大小为训练集理想输出；设置PSO初始数据为5个初始种群，总迭代次数为10，c1=c2=1.5，曲率调节参数η=1.74，空间维数d=4；分别对LSTM网络的隐含层层数、隐含层单元个数和学习率进行优化，最终优化结果为：设置LSTM网络结构为11个输入层，3个隐含层，隐含层含30个隐含单元，20个全连接层，1个输出层，学习率为0.01。

分别使用PSO-LSTM网络、LSTM网络、BP网络与改进后PSO-LSTM对同一实验数据的方位误差、俯仰误差进行预测对比。结果如图3所示，由图3可知改进后PSO-LSTM网络对方位角、俯仰角的误差预测较为准确，与实际值误差最大为0.037 3°。

图3 改进后PSO-LSTM网络对误差角预测Fig.3 Prediction of error values for angles by improved PSO-LSTM network

为了确定该网络的准确性、稳定性，选用均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)3个统计指标[10]，分别使用本文所述模型与未经PSO算法优化的LSTM网络模型[7]对同一数据参数进行预测仿真，并对比两者的误差指标，如表1所列。

表1 各网络模型预测性能对比Tab.1 Comparison of prediction performance of each network model

通过对比可以判断出：经过改进，网络预测性能有较为明显的提高，尤其是平均绝对百分比误差相比改进前提高了13.08%，由此可见基于改进后PSO-LSTM网络的太赫兹波束预判方法可以稳定提高链路余量。

4 结论

针对当前机械伺服机构难以满足太赫兹波束较窄特性的问题，提出了一种基于改进PSO-LSTM

深度网络的太赫兹波束预判方法，该方法通过建立深度网络模型，以历史指向误差数据为训练集，实时预测未来时刻的指向误差并进行修正，从而达到准确预测未来指向的目的。在建立深度网络模型中，本文改进了粒子群算法的惯性权重更新模式，提高算法的局部收敛能力，使深度网络的预测更加准确，通过实例分析，本文提出的网络预测性能优于LSTM网络模型。