等离子体随机分布对THz波传输特性的影响
2022-08-05杨光华
张 洁,杨光华
(西北师范大学 物理与电子工程学院,甘肃 兰州 730070)
临近空间高速飞行器再入大气层时,在强烈摩擦的作用下,飞行器周围会产生一层等离子体鞘套[1],该鞘套会影响通信质量,严重时甚至会引起信号完全中断,这种现象被称为“黑障”[2].如何缓解由等离子体鞘套引起的通信中断问题一直是航空航天领域的一个重要研究方向.
早期,对电磁波的传输特性研究中,常把等离子体看作是一种稳态介质[3-4],电磁波在稳态等离子体中的传输特性研究已经比较成熟[5-9],通常来说,等离子体电子密度服从一定的数学模型分布,如抛物线分布[10];双指数分布[11];高斯分布[12]和Epstein分布[13]等.许多学者采用散射矩阵法(Scattering matrix method, SMM)对电磁波在非均匀稳态等离子体的传输特性进行了研究[10-13].随着对等离子鞘套研究的深入,研究人员逐步认识到等离子鞘套具有明显的动态特性,等离子鞘套参数的动态分布特性与飞行器飞行姿态变化、压力脉动、烧蚀剥落等众多随机因素紧密相关.因此,更多的研究开始关注再入湍流等离子体的随机特性对电磁波产生的影响.Lei等考虑到等离子体电子密度的时变特性,提出了自适应多状态马尔可夫信道建模方法来描述再入等离子体鞘层对无线信道的动态影响[14].刘江凡等利用随机媒质的时域有限差分法将普通媒质的S-FDTD方法引申到等离子体色散媒质,基于该方法分析了电子密度的随机特性对电磁波传输的影响[15].Liu等利用混合矩阵法研究了在外加磁场的条件下,动态等离子体鞘层对电磁波传播特性的影响[16].
在以往的研究中,采用散射矩阵法研究的等离子体大部分被视为稳态介质[17],把等离子体密度假设成固定不变的,而利用此方法对等离子体随机特性的研究较少.文中在散射矩阵法的基础上,提出以高斯分布的电子密度特性的等离子体为基础,与蒙特卡罗方法[18]相结合,研究等离子体电子密度的随机分布对电磁波传输特性的影响.
1 理论模型
稳态等离子体电子密度分布模型采用典型的高斯分布,具体可描述为
(1)
其中,N0为电子密度峰值;x0为电子密度最大值时所在位置;d为等离子体厚度.
实际上,由于高超声速飞行器再入过程中产生的复杂热化学反应和飞行动力学行为使得等离子体电子密度在时空上不断变化并具有一定的随机性.在分析随机电子密度对电磁波传播的影响时,采用蒙特卡罗方法产生正态分布随机数,再结合稳态电子密度的分布,便可得出随机电子密度数学模型.其模型可以用下式表示为
Ne=ne_steady(x)(1+Δδne),
(2)
其中,Δ为等离子体电子密度相对变化幅度;δne为均值为0、方差为1的标准正态分布随机变量.图1所示为等离子体电子密度的分布模型.虚线为典型高斯分布模型,实线为随机分布模型.从图中可以看出,实线更符合等离子体鞘套中电子密度分布的随机特性.
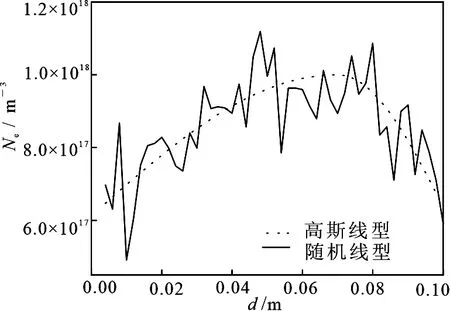
图1 等离子体电子密度分布模型
图2给出了电磁波在磁化等离子体中的分层传输模型,简单的将其分为3层,分别为自由空间-等离子体-自由空间.采用SMM,将等离子体划分为n层,入射区(0)和透射区(p)是自由空间,层与层之间具有不同的电子密度和碰撞频率,每一层的等离子电子密度可视作均匀的,外加磁场B的方向与电磁波的传播方向夹角为θ.
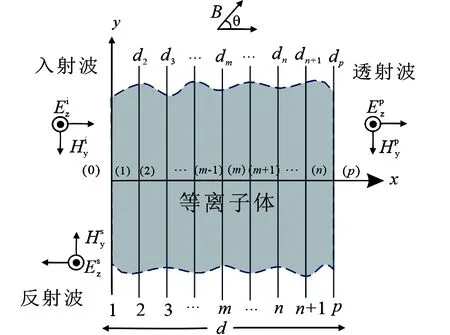
图2 电磁波在磁化等离子体中的分层传输模型
图2中每一层的传播常数可表示为
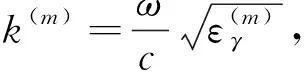
(3)
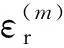
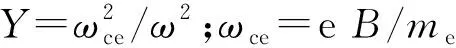
根据图2中的模型可以表示出各层的电场磁场分布,首先,(0)区域的电场可以表示为
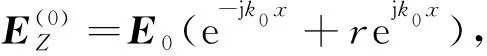
(5)
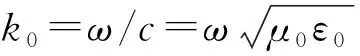
等离子体第m层中的电场分布可表示为
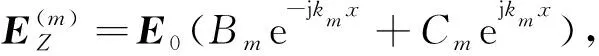
(6)
其中,Bm为第m层的透射系数;Cm为第m层的反射系数.同样,(p)区域的电场分布可以表示为
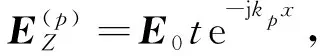
(7)
其中,t为总透射系数.此外,每一层的磁场分布也可通过麦克斯韦方程组得到.
根据x=0处的边界条件,可以得到矩阵方程
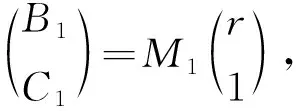
(8)
其中,

(9)
同理,匹配第m个界面处的边界条件,可得到矩阵方程为
其中,
x=d处的矩阵方程也可表示为
其中,
矩阵M1,Mm和Mp称为传递矩阵,通过(9)式、(11)式和(13)式可迭代计算出全反射系数r和透射系数t[20]为
其中,Mg1和Mg2来自于Mg,Mg被称为全局散射矩阵,可表示为
Mg为2×2矩阵,可以进一步将其转换为以下形式
Mg=(Mg1,Mg2),
(16)
其中,Mg1和Mg2分别表示矩阵Mg的第一列向量和第二列向量.
根据上述推导,可由R=|r|2,T=|t|2分别求得电磁波的反射率和透射率.总吸收率A也很容易通过下式得到
A=1-R-T.
(17)
2 数值结果与分析
THz 波在等离子体中的反射率非常低,透射率和吸收率的变化规律大致是相反的[19,21],透射率在一定程度上能更好地体现信号传输的能力[22],下面的内容主要对THz波在等离子体中的透射特性进行分析.
2.1 外加磁场对THz波透射特性的影响
将等离子体厚度设为d=0.1 m,并将其划分为50层,图3所示为磁化角度对THz波透射率的影响.其中,碰撞频率为fν=0.1 THz,最大电子密度为N0=5×1017m-3,外加磁场强度为B=7 T,电子密度相对变化幅度取Δ=10%.从图3可以看到,在同一磁化角度下,随频率f的不断增大左极化波的透射率随之增大,而右极化波在频率f<2×1011Hz时的透射率基本逐渐减小,在频率f>2×1011Hz时的透射率逐渐增大.在相同的磁化角度下,左、右极化波的变化趋势会不同,这是由于在外加静态磁场的情况下,等离子体中的电子受到磁场作用做回旋运动,而右极化波会与回旋运动的电子同步旋转形成回旋共振,此时的电磁波频率有一个临界值fc,在频率fc=2×1011Hz处电磁波能量被大量吸收透射率也最小.还可以看出,在全频带上,左极化波的透射率随磁化角度的增大而减小,而右极化波在频率f较高时,透射率随磁化角度的增大而增大.在磁化角度θ=0°时左极化THz波的透射率最大,而θ=90°时右极化 THz 波的透射率最大.以此为依据,在研究等离子体电子密度和碰撞频率对THz波传输带来的影响时,分别以磁化角度θ=0°和θ=90°对左极化波和右极化波在等离子体中的传输特性进行分析.
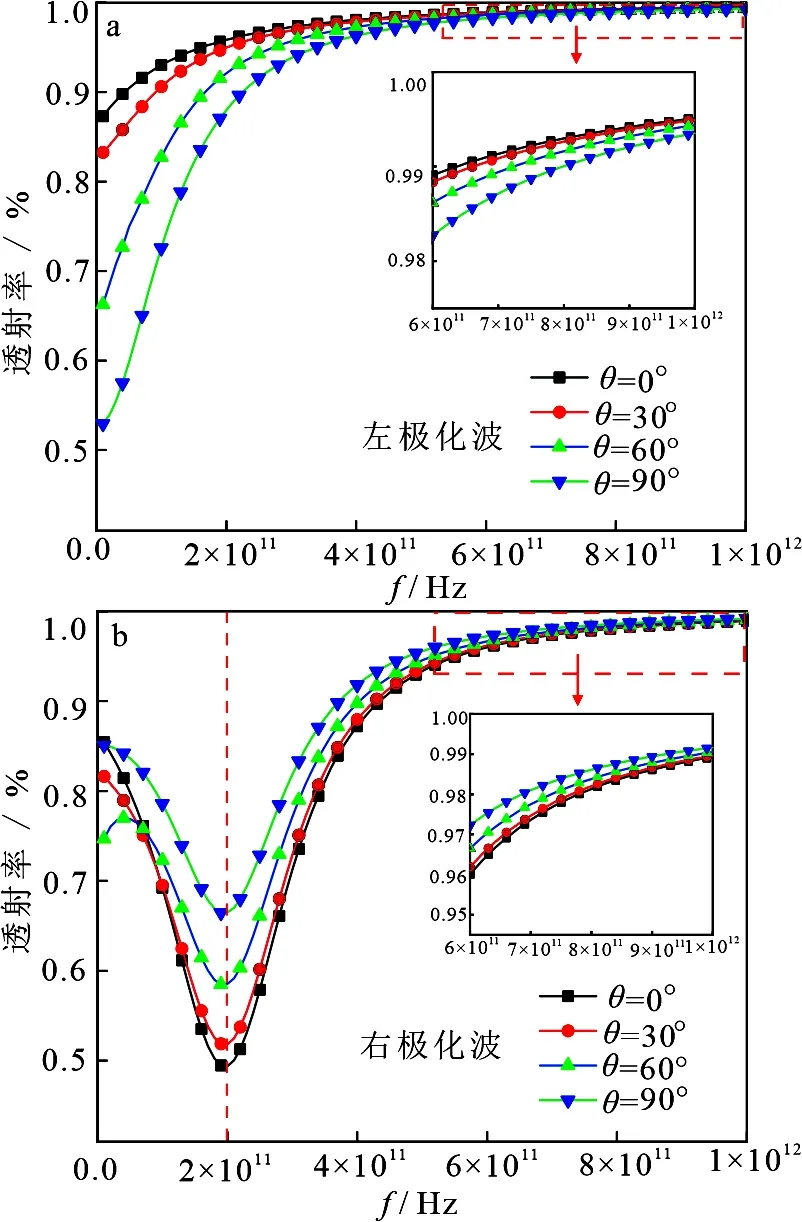
图3 磁化角度对 THz 波透射率的影响
图4给出了外加磁场强度对THz波透射率的影响,其中碰撞频率fv=0.1 THz,最大电子密度为N0=5×1017m-3,等离子体厚度d=0.1 m,电子密度相对变化幅度取Δ=10%,外加磁场强度范围在1~7 T[23-24].在图4a中左旋极化波的透射率在整个频带上随外加磁场强度的增大而增大.而在图4b中,右极化波的透射率在低频端和高频端呈现不同的变化趋势,在低频端,右极化波的透射率随外加磁场的增大而增大.但由于频率fc的大小与外加磁场强度有关,外加磁场强度越大,频率fc的值越大,这使得电磁波的能量更多的被吸收,导致右极化波的透射率随外加磁场的增大而减小.当后文中出现外加磁场强度B=7 T时,默认频率fc=2×1011Hz,后文提及fc时不再单独说明大小.
图5给出了不同磁化角度和外加磁场强度对THz波透射率的影响,从图中可以看到磁化角度和外加磁场同时变化也可对 THz 波的透射率产生影响.在图5a中,磁化角度分别为θ=30°和θ=60°时,均为外加磁场强度B=5 T时 THz 波的透射率大.
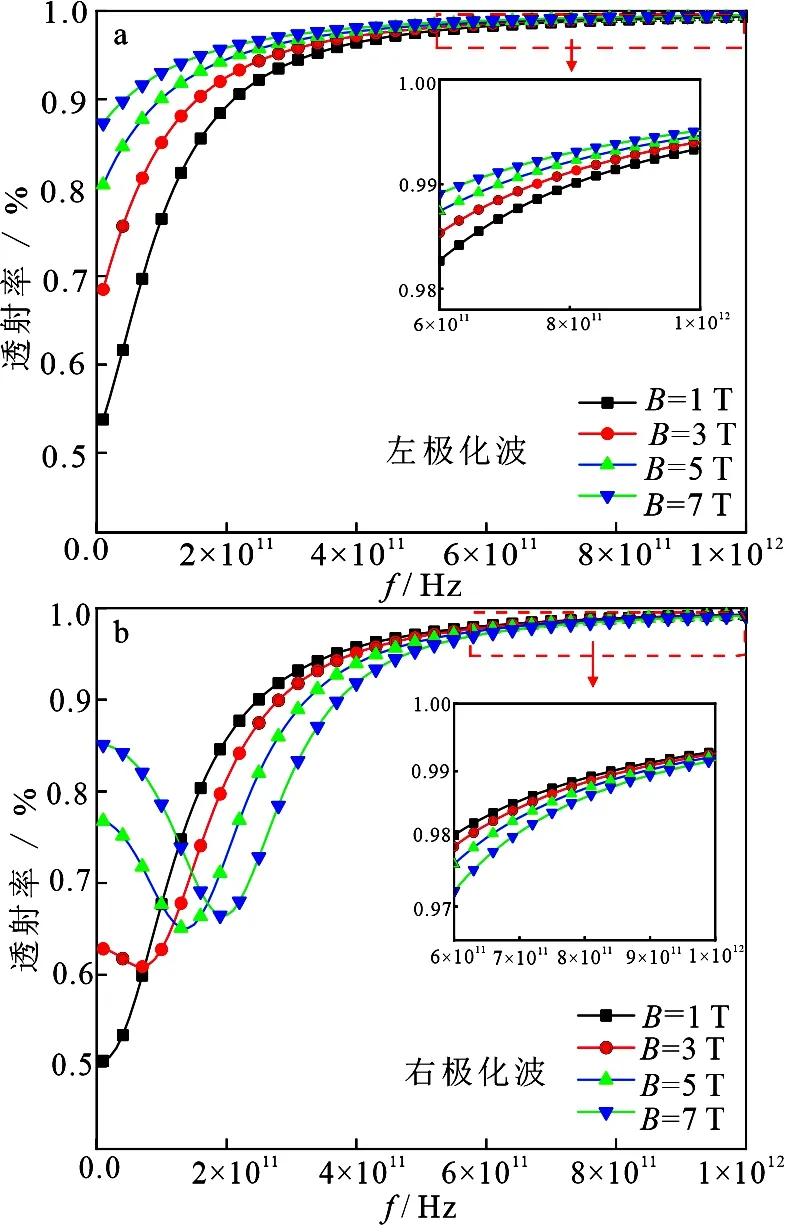
图4 外加磁场强度对 THz 波透射率的影响
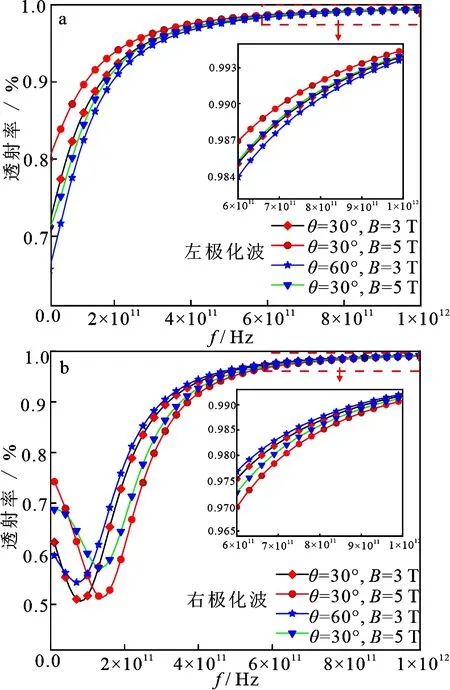
图5 不同磁化角度和外加磁场强度对THz波 透射率的影响
外加磁场强度分别为B=3 T和B=5 T时,均为磁化角度θ=30°时 THz 波的透射率大.也就是说,左极化波在相同磁化角度下,外加磁强度越大透射率越大,在相同外加磁场强度下,磁化角度越小,透射率越大.在图5b中频率f较大时,磁化角度分别为θ=30°和θ=60°时,均为外加磁场强度B=3 T时 THz 波的透射率大.外加磁场强度分别为B=3 T和B=5 T时,均为磁化角度θ=60°时 THz 波的透射率大,这与左极化波的变化规律刚好相反.因此,减小磁化角度并增大外加磁场强度,有利于左极化THz波在具有随机特性等离子体中的传输,增大磁化角度并减小外加磁场强度,有利于右极化THz波在具有随机特性等离子体中的传输,且在同一磁化角度和外加磁场强度下,左极化波的透射率高于右极化波.
2.2 等离子体电子密度对THz波透射特性的影响
图6给出了等离子体最大电子密度对THz波透射率的影响,其中碰撞频率为fν=0.1 THz,外加磁场强度B=7 T,等离子体厚度d=0.1 m,电子密度相对变化幅度取Δ=10%.从图中可以看出,当最大电子密度一定时,左极化波的透射率随频率f的增大而增大,而右极化波由于回旋共振的影响在频率f
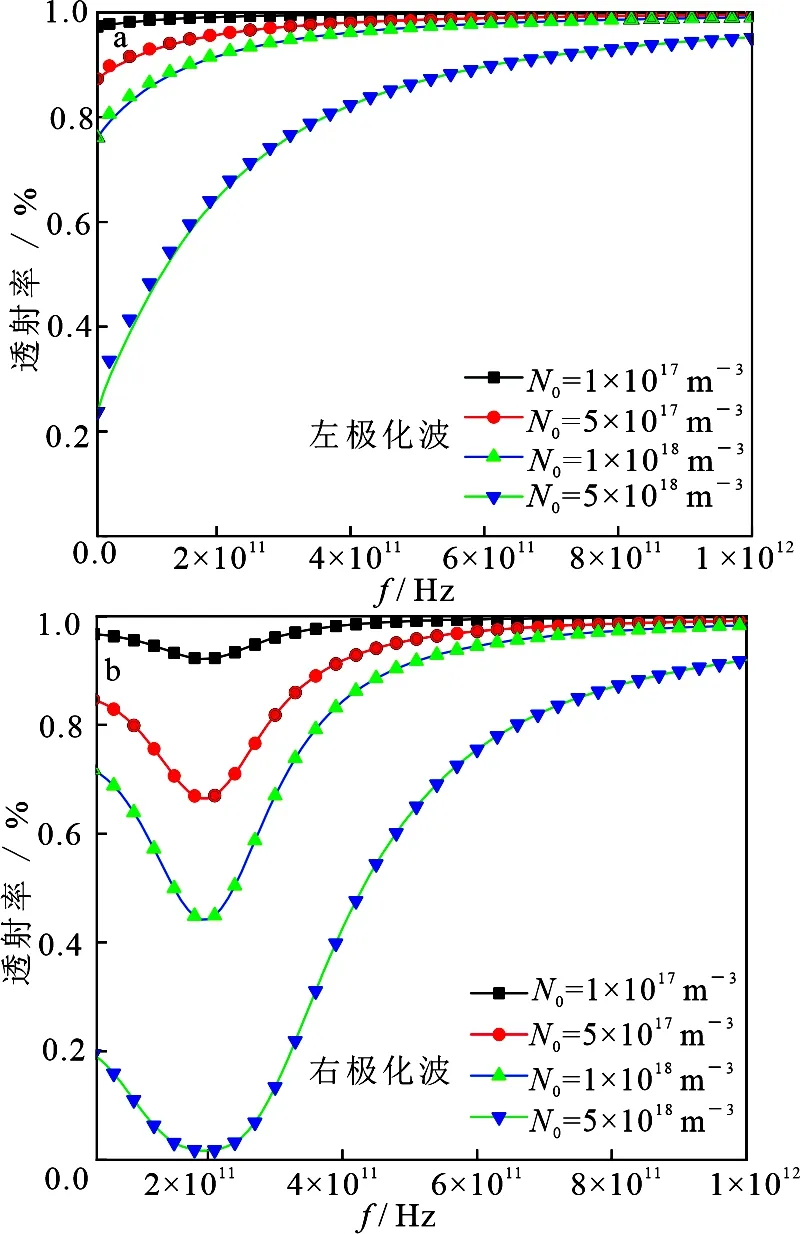
图6 等离子体最大电子密度对 THz 波透射率的影响
图7给出了等离子体电子密度相对变化幅度对THz波透射率的影响,其中碰撞频率为fν=0.1 THz,外加磁场强度B=7 T,等离子体厚度d=0.1 m.最大电子密度N0=5×1017m-3.图7a和图7c为 THz 波透射率随等离子体电子密度相对变化幅度变化的等值线图,为更好观察其变化规律,图7b和图7d中给出了几个特定电子密度相对变化幅度值时透射率随 THz 频率变化的曲线.对于左极化波,从图7a中可以看出,随频率f的增大,透射率数值所代表的色阶宽度变宽且数值变大,随电子密度相对变化幅度的增大,在低频端透射率数值所代表的色阶出现明显的色差,在高频端透射率数值所代表的色阶色差逐渐消失.也就是说,各电子密度相对变化幅度的THz波透射率随频率f的增大而增大最后逐渐相等,电子密度相对变化幅度对低频端THz波的透射率影响较大,而对高频端 THz 波的透射率影响较小.从图7b中还可看出,电子密度相对变化幅度越大THz波透射率越大.对于右极化波,从图7c中可以看出,在频率f=fc时,透射率数值所代表的色阶色差较大,且随电子密度相对变化幅度的增大,透射率色阶数值越大.也就是说,当频率f=fc时,右极化波在回旋共振处的电子密度相对幅度对THz波透射率的影响最大,且电子密度相对变化幅度越大,THz波的透射率越大.另外,对于左、右极化波,在全频带上电子密度相对变化幅度越大,THz波的透射率越大,且在同一电子密度相对变化幅度下,左极化波的透射率高于右极化波.
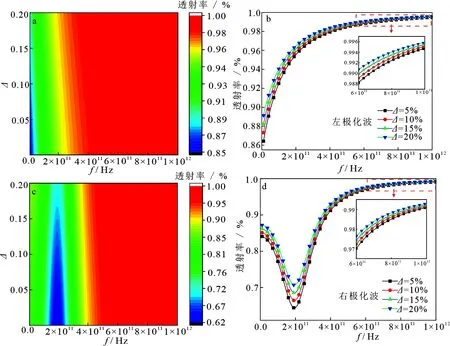
图7 等离子体电子密度相对变化幅度对 THz 波透射率的影响
等离子体电子密度对THz波的影响涉及到最大电子密度与电子密度相对变化幅度这两个因素,当这两个因素共同变化时,THz波的透射率发生了明显变化.在图8a和图8b中明显可以看到透射率较大的两条曲线最大电子密度为N0=1×1017m-3,且电子密度相对变化幅度为Δ=20%.也就是说,在全频带上等离子体最大电子密度越小并且电子密度相对变化幅度越大,左、右极化THz波的透射率越大.
2.3 等离子体碰撞频率对THz波透射特性的影响
图9给出了等离子体碰撞频率对THz波透射率的影响,其中,外加磁场强度B=7 T,等离子体厚度d=0.1 m,最大电子密度N0=5×107m-3,电子密度相对变化幅度取Δ=10%.从图9a中可以看出,在全频带上左极化波的透射率随频率f的增大而增大,且碰撞频频率越小,透射率越大.而在图9b中,右极化波在频率f
3 结论
采用散射矩阵法模拟了THz波在具有随机特性等离子体中的传播,研究了磁化角度、外加磁场强度、最大电子密度和电子密度相对变化幅度以及碰撞频率对THz波透射率的影响,得出以下结论:
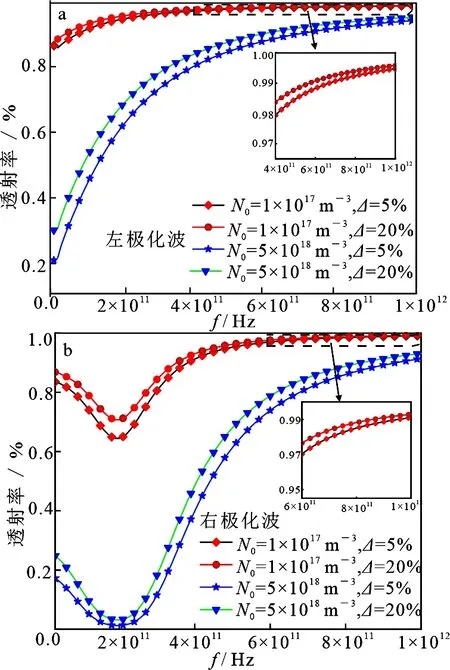
图8 不同等离子体最大电子密度和电子密度相对 变化幅度对 THz 波透射率的影响
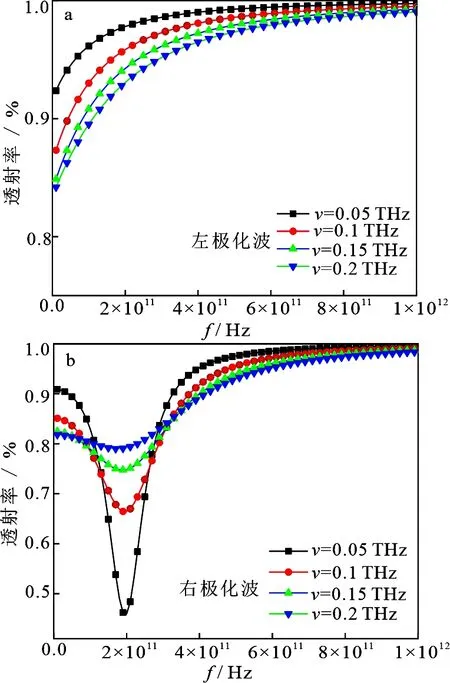
图9 等离子体碰撞频率对THz波透射率的影响
1)在外加磁场的作用下,由于右旋极化波在传输时受回旋共振作用的影响,右极化波的透射率变化趋势比左极化波更复杂,且右旋极化波透射率出现谷值,谷值随外加磁场强度的增大而增大并往高频端方向移动.磁化角度对左、右极化波透射率的影响刚好相反,减小磁化角度并增大外加磁场强度有利于左极化THz波在具有随机特性等离子体中的传输,增大磁化角度并减小外加磁场强度有利于右极化波THz波在具有随机特性等离子体中的传输.
2)在全频带上,等离子体最大电子密度越小,电子密度相对变化幅度越大,左、右极化THz波在具有随机特性等离子体中传输的透射率越大.电子密度相对变化幅度对低频端THz波的透射率影响较大,特别是在右极化波受回旋共振作用时影响最大.基于该结果,对于在较低频率时提高THz波透射率给出了建议.
3)增大碰撞频率并不利于THz波的透射.另外,左极化波在具有随机特性等离子体中传播的透射率高于右极化波.这些理论结果应用于实践中时,可以选择调控合适的物理量来改变THz波在等离子体中的透射,从而缓解“黑障”现象.
