三体作用下玻色-爱因斯坦凝聚中的PT-对称孤子

漆 伟，李 明，郭晓刚

(陕西科技大学 文理学院,陕西 西安 710021)

1998年,Bender研究发现当势满足PT对称时，非厄米系统可以产生实谱[1].PT对称势V(x)要求满足条件V(x)=V*(-x).在这样的系统中，势的虚部代表粒子与外部环境的相互作用.目前，很多学者对于非厄米PT对称系统展开了研究，比如具有PT对称势BEC中的涡旋[2]；双模近似下的PT对称量子系统的BEC[3]；PT双势阱中非线性量子动力学的研究等[4].

孤子是一种常见的非线性现象，在等离子体物理、非线性光学、电磁学、生物学、天体物理、固体物理以及玻色-爱因斯坦凝聚体等众多领域广泛存在[5-10].随着在BEC中陆续发现亮孤子，暗孤子和涡旋孤子[11-14].关于BEC中物质波动力学性质的研究成为当前重要课题之一[15-19].

BEC的动力学行为受到原子间相互作用的显著影响.BEC中原子间两体相互作用强度主要通过s-波散射长度a描述，当a>0时，原子间互相排斥，当a<0时，原子间互相吸引.实验上，通过Feshbach共振技术调节s-波散射长度的大小，研究两体相互作用[20].当原子密度较低时，原子间距远大于原子间相互作用的距离，两体相互作用将起主要作用，而三体相互作用可以忽略[21].当原子密度较高时，原子间距变小，三体相互作用将发挥重要作用[22]，比如在集成原子光学器件中[23].实验观察，即使三体相互作用的强度很小，也可以使凝聚体粒子数明显增多.实验上，通过Feshbach共振技术调节两体和三体相互作用，获得三体相互作用占主导的BEC.考虑原子密度较高时，三体相互作用对BEC动力学性质的影响.

文中首先得到描述在平均场近似下具有两体和三体相互作用束缚于PT对称势中BEC动力学性质的3～5次Gross-Pitaevskii(GP)方程.然后提出了适用于非厄米系统的变分方法，解析得到孤子的化学势，宽度和密度分布的表达式.之后讨论三体相互作用对孤子的密度分布，宽度和化学势的影响.

1 理论模型

考虑具有两体和三体相互作用的BEC被束缚在PT对称的外势中，在平均场近似下BEC的动力学行为可由如下的GP方程描述[24]

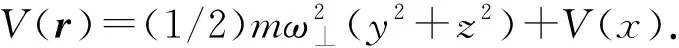
对(2)式做无量纲化处理[25]，令

为了简便,省略两体和三体相互作用的系数以及变量上方的波浪线，用t代替τ.这个雪茄形凝聚体的动力学行为由如下准一维的GP方程来描述

其中，V(x)满足条件V(x)=V*(-x)，势的形式为V(x)=VR(x)+iV1(x).选择高斯型势VR=-Vrexp(-x2)作为PT对称势的实部，高斯型势在实验上较容易实现[26].选择V1=-Vixexp(-x2)作为PT对称势的虚部,虚部代表了增益损耗机制.除了利用光偶极阱外[27],还可以利用泵浦方案来实现增益损耗机制.

2 变分法

应用变分法研究非厄米的耗散系统.假设Ψ=φ(x)exp(-iμt)，代入(3)式得

(4)式左边部分对应保守的拉格朗日量

取试探解的形式如下:

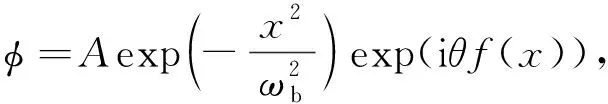
(6)

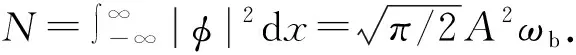
将(8)式化简成含有粒子数N的形式，

(9)式等式右边的最后两项分别源自于两体和三体相互作用.对含有耗散项的系统的变分法可以根据文献[28]和文献[29]修改为如下形式

其中，φ=N,ωb,θ.(10)式中Q=iV1(x)φ代表系统与外部环境的增益损耗.

令φ=N，从(10)式得到化学势μ的表达式为

(11)式右边第一项源于相位分布θf(x)，第二项源自于色散传播，第三项和第四项分别源自于两体和三体相互作用，方程的最后一项源自于势VR.上式表明两体和三体相互作用在对化学势的影响上存在竞争关系.

令φ=ωb，从(10)式得到凝聚体宽度ωb的表达式

(12)式左边表明粒子色散(第一项)，两体相互作用(第二项)和三体相互作用(第三项)共同决定了凝聚体的宽度.由上式可知三体相互作用极大影响了凝聚体的宽度，等式右边的第一项源自于孤子的非齐次相位.等式右边的第二项源自于势VR对凝聚体宽度的影响.

最后，令φ=θ，得到孤子的相位θ的表达式

从(13)式可知，孤子的相位不受原子间相互作用的影响.对于纯实数势(V1=0)，孤子的相位分布是沿x轴的平面.

接下来，利用变分的结果重点讨论三体相互作用对孤子性质的影响.

3 讨论分析

为了研究三体相互作用对孤子形状，宽度和化学势的影响，取f(x)=tanh(x)并代入到(6)式中[30].从(11)，(12)，(13)式依次得到孤子的化学势，粒子数和相位的表达式.为了便于研究三体相互作用对于孤子性质的影响，取g0=-1的特殊情况.对于一个固定的两体相互作用强度，存在一个正的临界三体相互作用强度χc，当三体相互作用强度大于χc时，孤子将不能稳定存在.例如，当取g0=-1,ωb=0.7时，临界三体相互作用强度χc的值为0.02.对于一个固定的ωb，当三体相互作用强度χ0≤0时，对应的粒子数N和化学势μ是唯一的.但当χc>χ0>0时，则存在两个粒子数N及其对应的两个化学势μ.取其中粒子数N较小的分支称为“普通”分支，而粒子数N较大的分支称为“超常”分支.图1给出了χ0≤0和χ0>0的“普通”分支的化学势μ随粒子数N的变化曲线.

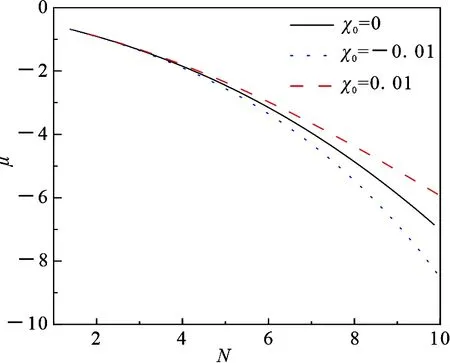
图1 χ0取不同值时化学势μ随粒子数N的变化

当粒子数N较小时，取不同的三体相互作用强度χ0对于化学势μ的影响较小.随着粒子数N的增大，当χ0=0.01时，三体相互作用导致化学势μ增大；当χ0=-0.01时，三体相互作用导致化学势μ减小.随着粒子数N的增加，三体相互作用对化学势μ的影响越来越重要.

图2给出了χ0≤0和χ>0的“普通”分支的孤子宽度ωb随粒子数N的变化曲线.当粒子数N较小时，不同的三体相互作用强度χ0对于宽度ωb影响较小.随着粒子数N的增加，当χ0=0.01时，三体相互作用导致孤子宽度ωb变宽，当χ0=-0.01，三体相互作用导致孤子宽度ωb变窄.随着粒子数N的增加，三体相互作用对孤子宽度ωb的影响也越来越重要.

图3给出了χ0≤0和χ0>0的“普通”分支，不同的三体相互作用强度χ0对于孤子密度分布|φ|2的影响.当χ0=0.01时，三体相互作用导致孤子密度|φ|2增大.当χ0=-0.01时，三体相互

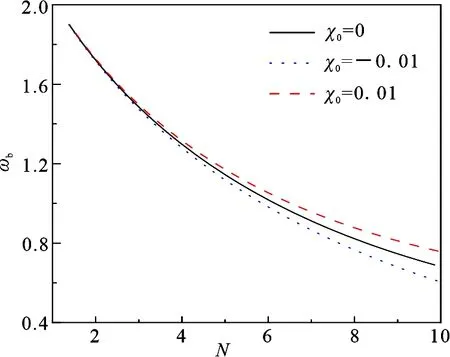
图2 χ0取不同值时孤子宽度ωb随粒子数N的变化

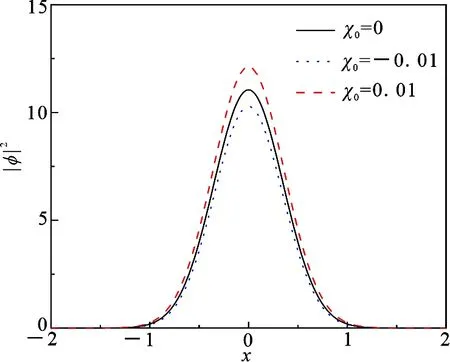
图3 χ0取不同值时孤子的密度分布 (μ=-6.66时的波形)

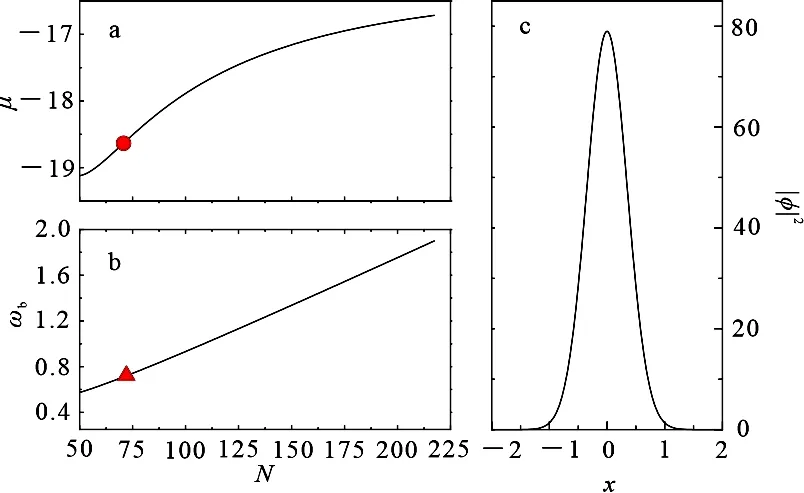
图4 χ0=0.01,g0=-1时“超常”分支的化学势μ 和孤子的宽度ωb随粒子数N的变化及 孤子的密度分布

作用导致孤子密度|φ|2减小.微小的三体相互作用强度的改变将会显著影响孤子的密度分布|φ|2.

图4a和图4b给出了当χ0=0.01,g0=-1时“超常”分支的化学势μ和孤子宽度ωb随粒子数N的变化曲线.从图中可知，化学势μ随着粒子数N的增长呈非线性关系.孤子的宽度ωb随着粒子数N的增长呈线性关系.图4c给出了局域孤子的密度分布，相关参数对应于图4a和图4b中标记处.从图4c和图3中x0=0.01的|φ|2对比可知，“超常”分支的粒子数N远远大于“普通”分支的粒子数N.

通常使用Vakhitov-Kolokolov(VK)稳定性判据来验证一维局域GP孤子的稳定性.VK判据是根据孤子的粒子数与对应化学势的导数的符号来确定孤子的稳定性.若dN/dμ>0，则对应的孤子是稳定的.若dN/dμ<0，则孤子将不能稳定存在.目前，VK判据也可以推广到具有复杂外势的非线性薛定谔方程来预测稳定性[31].χ0≤0和χ>0的“普通”分支的dN/dμ总是负的，对应的孤子是不稳定的.χ0>0的“超常”分支的dN/dμ总是正的，对应的孤子是可以稳定存在的.当g0=-1时，原子间的两体相互作用是吸引力，为了使孤子稳定存在，则需要一个正的三体相互作用引起的排斥力来阻止系统的坍塌，因此当三体相互作用强度位于参数区间χc>χ0>0时，存在一个稳定的亮孤子.

4 结束语

文中研究了束缚于PT对称势中具有三体相互作用BEC中孤子的稳定性.在平均场近似下，系统的动力学性质可以用3～5次的GP方程描述.应用变分法解析得到PT对称孤子的密度分布，宽度和化学势的表达式.绘制了化学势和孤子宽度随粒子数的变化曲线.发现正的三体相作用使孤子的宽度和化学势变大，而负的三体相互作用则相反.通过Feshbach共振技术调节两体和三体相互作用，发现微小的三体相互作用强度的改变显著影响孤子的密度分布.当g0=-1时，两体相互作用是吸引力，为使孤子稳定存在,则需要一个正的三体相互作用引起的排斥力来阻止系统的坍塌，使系统稳定.当三体相互作用强度位于参数区间χc>χ0>0时，将会出现一个稳定的亮孤子.通过VK稳定性分析，进一步证明该孤子是稳定存在的.