具有时滞的分数阶半线性微分包含的可控性
2022-08-05杨和,任倩
杨 和,任 倩
(西北师范大学 数学与统计学院,甘肃 兰州 730070)
0 引言
近年来,分数阶微分方程由于在物理学、力学和工程领域的广泛应用而引起了人们的极大关注.2010年,Hernandez等[1]运用积分方程解算子理论研究了带有分数阶导数的抽象方程解的存在性问题;Zhou等[2-3]用拉普拉斯变换和概率密度函数给出了抽象分数阶发展方程mild解的定义,并证明了其存在性定理.关于分数阶微积分和分数阶微分方程的更多结论可参见文献[4-5].
分数阶微分包含在应用中具有更广泛的实际意义.2011年,Wang等[6]讨论了分数阶半线性微分包含初值问题

非局部条件与传统的初值条件相比,具有更加广泛的应用背景.近年来,在半群{T(t),t≥0}非紧条件下微分方程可控性问题的研究可见文献[7-8].2018年,Alsarori等[9]用非紧性测度工具和多值映射的不动点定理讨论了Banach空间X中的分数阶半线性脉冲微分包含非局部问题

据我们所知,关于含时滞分数阶微分包含精确可控性的研究相对较少,主要原因在于:研究无穷维空间中微分方程的精确可控性时,通常假设相应的线性算子生成的半群是非紧的,此时非线性项要么满足Lipschitz条件,要么满足非紧性测度条件;而当方程中含有时滞项时,在非紧性测度条件下证明解算子的紧性是困难的.
受上述文献启发,文中在Hilbert空间(X,||·||)中研究具有时滞的分数阶微分包含非局部问题
(1)

文中引入一个新的Banach空间(Λ,||·||Λ),其中
在非紧半群条件下,当非线性项含时滞项时,克服了用非紧性测度方法证明解算子紧性的困难,在非局部函数g全连续时,用不同于文献[6]的方法,在相应的线性微分方程初值问题精确可控的条件下,证明了系统(1)的精确可控性.
1 预备知识

定义1[6]设函数x∈C,若存在f∈L1(J,X),使得对∀t∈J,f(t)∈F(t,xt)满足
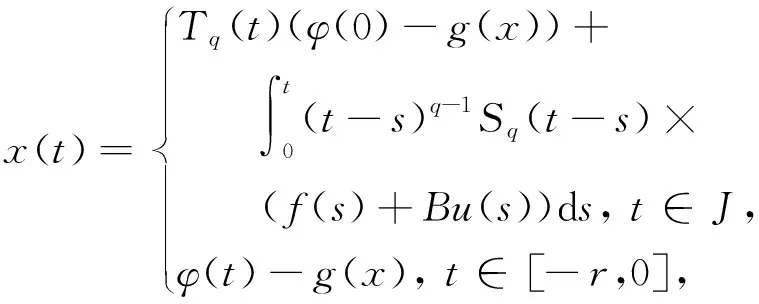
(2)
则称x是系统(1)的mild解,其中

注1当ν∈[0,1]时,有
引理1[8]有界线性算子族Tq(t)和Sq(t)具有以下性质:
( i )对任意给定的t≥0和∀x∈X,有
( ii )对∀t≥0,算子Tq(t)和Sq(t)都是强连续的;
(iii)如果T(t)(t≥0)是等度连续半群,则对∀t>0,算子Tq(t)和Sq(t)都是等度连续的.
定义2[10](精确可控性) 若对任意的xb∈X,存在控制函数u∈L2(J,U),使得非局部问题(1)的mild解x满足x(b)=xb,则称非局部问题(1)在区间J上是精确可控的.
首先考虑非局部问题(1)相应的分数阶线性微分方程初值问题
(3)
定义线性初值问题(3)的控制算子如下:


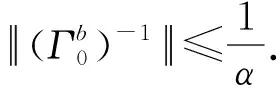
设D是X的有界子集,定义其Hausdorff非紧性测度为:
β(D):=inf{ε>0:D在X中有有限ε-网}.
引理3[11]设集合C⊆X,D⊆X均有界,则
( i )β(D)=0⟺D为相对紧集;
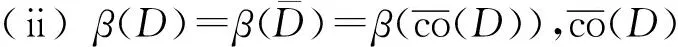
(iii)D⊂C⟹β(D)≤β(C);
(iv)β(D+C)≤β(D)+β(C),其中D+C={x:x=y+z,y∈D,z∈C};
(v)β(D∪C)≤max{β(D),β(C)};
(vi)β(λD)≤|λ|β(D),∀λ∈R,其中λD={x:x=λy,∈D};

引理4[11]若W⊆C(J,X)是有界且等度连续集,则β(W(t))在J上连续,且
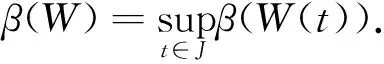
引理5[12]设X为可分的Banach空间,D={xn}⊂C(J,X)为可列集.若存在φ∈L1(J,X),使得||xn(t)||≤φ(t),a.e.t∈J,n=1,2,…,则β(D(t))在J上可积,且
下面介绍一些关于多值映射的定义和基本结论,更多关于多值映射的内容可参见文献[13].
定义3设X,Y是两个拓扑空间.

(2)若对任意有界子集D⊆X,F(D)相对紧,则称F全连续;
(3)若对任意开子集V⊆Y,F-1(V)={x∈X:F(x)⊆V}是X的开子集,则称F上半连续(简记为usc);
(4)若F的图GF={(x,y)∈X×Y:y∈F(x)}是拓扑空间X×Y的闭子集,且xn→x,yn→y,yn∈F(xn)蕴含y∈F(x),则称F是闭的;
(5)若存在x∈X使得x∈F(x),则称x是F的一个不动点.
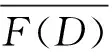


是C(J,X)×C(J,X)中的闭图算子.
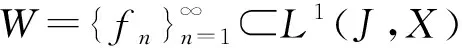
(1)W可积有界,即存在ω∈L1(J,R+),使得
||fn(t)||≤ω(t), a.e.t∈J;
(2)集合{fn(t):n∈N}在X中相对紧a.e.于J,则称序列W半紧.
引理8[13]L1(J,X)中的每个半紧序列是弱紧的.
引理9[6]对∀θ∈(0,1],0 |aθ-bθ|≤(b-a)θ. 定义集合 其中Pb(Λ)表示Λ的非空有界子集.容易验证βΛ为Λ上Hausdorff非紧性测度. 首先引入如下假设条件: (C1)算子A生成一个等度连续半群{T(t),t≥0}. (C3)存在常数q1∈(0,q)和函数m∈L1/q1(J,R+),使得 (C4)存在常数L>0,使得对C([-r,0],X)中的任意非空有界集D,有 βX(F(t,D))≤LβC([-r,0],X)(D). (C7)分数阶线性微分方程初值问题(3)在区间J上精确可控. 对∀xb∈X,定义控制函数u如下: (4) 其中 其中f∈SF,x.由条件(C3),(C5)~(C7)直接计算可得 当t=b时,有 由定义2可知,控制系统(1)精确可控.因此要证明控制系统(1)精确可控,只需证明控制系统(1)存在相应于控制函数u的mild解. 定理1设条件(C1)~(C7)满足.如果 (6) 则控制系统(1)在区间J*上精确可控. Ψ(x)={ψ∈Λ:ψ(t),f∈SF,x}, 其中 由引理10可知,控制系统(1)的mild解等价于算子Ψ的不动点.下面分四步证明Ψ至少有一个不动点. 第一步.证明Ψ有闭凸值. 首先证明对∀x∈Λ,Ψ(x)是凸的. 设ψ1,ψ2∈Ψ(x),存在f1,f2∈SF,x,使得对∀t∈[-r,0],λ∈[0,1],有 λψ1(t)+(1-λ)ψ2(t)=φ(t)-g(x). 所以当t∈[-r,0]时,λψ1+(1-λ)ψ2∈Ψ(x). 对∀t∈J,因为 所以对λ∈[0,1],有 因为F有凸值,所以SF,x是凸的,即 λf1+(1-λ)f2∈SF,x. 因此 λψ1+(1-λ)ψ2∈Ψ(x), 所以Ψ(x)是凸的. 其次证明对∀x∈Λ,Ψ(x) 是闭的. (7) 其中 由条件(C3),对∀n≥1和几乎所有的s∈J,有 ||fn(s)||≤m(s), 对∀t∈J,n≥1,有 由Hölder不等式,有 因此,(7)式两边让n→∞,则由(5)式和Lebesgue控制收敛定理,有 因此,由Ψ(x)的定义可知,ψ∈Ψ(x). 当t∈[-r,0]时,由条件(C6),有 ||ψ(t)-x0(t)||≤η<δ. 当t∈J时,由条件(C3)和引理1(i),有 由φ的连续性,对∀σ>0,t,t+σ∈[-r,0],有 其中I:X→X为恒等算子,所以 由引理1(ii)知,Tq(t)(t≥0)是强连续的,所以当h→0时I1→0.由引理1(i)和条件(C3),有 由引理9,条件(C3)和(5)式,有 因此 由引理1知,当t>0时,Sq(t)是等度连续的,所以由条件(C3)和(5)式,有 其中 当t∈[-r,0]时,由g的紧性,有 βX(ϑ(t))=βX({φ(t)-g(xk):k≥1})=0. 当t∈J时,由g的紧性,有 βX({Tq(0)(φ(t)-g(xk)):k≥1})=0. 因此,由引理4可得 由引理5和条件(C4),有 其中 因此 所以,将(9)式代入(8)式,由(6)式可得 重复上述步骤可得 由(6)式知M**<1,上式两边让n→∞,则有 第三步.证明Ψ有闭图. 需证存在f*∈SF,x*,使得 由g的连续性可知,当xn→x*时,对∀t∈[-r,0],有 φ(t)-g(xn)→φ(t)-g(x*). 当t∈J时, 算子G是线性连续的,由引理7,G∘SF是一个闭图算子,且Gfn∈GSF,xn.当xn→x*时,再由引理7,有 这意味着ψ*∈Ψ(x*). 例1考虑具有时滞的分数阶微分包含 (10) 其中CD1/2为q=1/2阶Caputo型分数阶导数,J:=[0,ω],ω为常数,b是适当定义的函数. 取X:=L2([0,1],X),控制函数的取值空间U=X.设 作X中的算子A: 由文献[9]可知,A生成X中的等度连续半群T(x)(t≥0).这样系统(10)可化为形如系统(1)的分数阶微分包含可控性问题.若系统(10)满足条件(C2)~(C7),则由定理1可知系统(10)在区间J*上精确可控.
2 主要结果




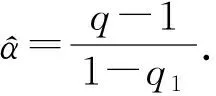

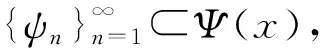


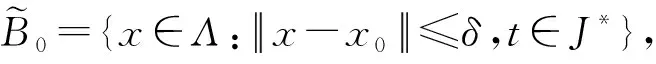


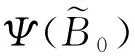
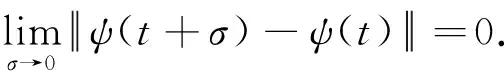


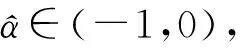

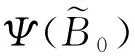
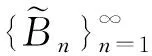
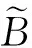



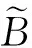
3 应用
