圆柱体上二阶椭圆特征值问题的有效Galerkin谱逼近
2022-08-05牟宴铭
牟宴铭,安 静*
(贵州师范大学 数学科学学院,贵州 贵阳 550025)
0 引言
特征值问题在流体力学、结构力学、随机过程和量子力学等领域有重要的物理背景和广泛的应用[1-3],其数值计算方法一直是很多学者关注和研究的课题.到目前为止,已经有很多数值方法求解特征值问题,主要包括有限差分法[4-5]、有限元法[6-8]、谱方法[9-11]等.然而,对于一些特殊的计算区域,如球域、椭球域、柱体区域等,直接利用差分法或有限元法求解是比较困难的.主要原因是这些区域都带有曲面边界,区域剖分比较复杂,边界附近单元上的差分逼近或有限元基函数的构造也比较复杂.另外,由于计算区域是三维区域,要获得较高精度的数值解需要较高的时间复杂度和大量的内存空间.
近年来,谱方法已经成为计算微分方程数值解的一类重要方法[12-14],将谱方法应用于这些特殊区域上的特征值问题是一件有意义的事情.文中提出了三维柱体域上二阶椭圆特征值问题的一种新的谱逼近方法.首先,将直角坐标系下的二阶椭圆特征值问题转化为柱坐标系下的等价形式,再利用变量分离方法将原问题转化为矩形区域上的一系列二维特征值问题;其次,针对实心圆柱体和空心圆柱体两种情况,分别引入了两种Sobolev空间和相应的多项式逼近空间,对每个降维的二维特征值问题建立了变分形式和离散格式;然后,利用全连续算子的谱理论和非一致带权Sobolev空间中投影算子的逼近性质证明了逼近解的误差估计.另外,通过构造逼近空间的一组有效基函数,推导了离散格式基于张量积的矩阵形式.最后,给出了一些数值算例,数值模拟结果表明我们的算法是有效的和高精度的.
1 降维格式和极条件
作为一个模型问题,考虑二阶椭圆特征值问题

(1)
(2)
其中Ω是实心圆柱体或空心圆柱体区域,β是一个非负常数.下面将推导问题(1)~(2)基于柱坐标变换的降维格式.

x=rcosθ,y=rsinθ,z=z,
其中R1 首先考虑R1=0的情况,问题(1)~(2)可重述为 (4) (5) 其中(r,θ,z)∈G,G=(0,R2)×[0,2π)×(-1,1),φ(r,θ,z)=u(rcosθ,rsinθ,z).由于φ在θ方向上是2π周期的,所以由傅里叶基函数展开可得 (6) 将(6)式代入(3)式,有 由于柱坐标变换在r=0处引入了奇性,为了保证方程(4)的适定性,φm(r,z)需要满足极条件 m2φm(r,z)|r=0=0, 即 φm(0,z)=0,m≠0. 将(6)式代入(4)式,利用傅里叶基函数的正交性可以得到一系列等价的二维特征值问题: (8) (9) (10) 其中(r,z)∈(0,R2)×(-1,1).令 则问题(8)~(10)进一步化为下面等价形式: 其中(t,z)∈D,D=(-1,1)×(-1,1)=I2. 类似地,当R1>0时,有 (14) (15) 其中(r,θ,z)∈W,W=(R1,R2)×[0,2π)×(-1,1),θ∈[0,2π),φ(r,θ,z)=u(rcosθ,rsinθ,z).类似于R1=0的推导,可以得到一系列等价的二维特征值问题 (16) (17) 其中(r,z)∈(R1,R2)×(-1,1).令 则问题(16)~(17)进一步化为如下等价形式: 其中(t,z)∈D. 仅考虑m≥0的情况,m<0的情况可以类似地推导.为了推导问题(11)~(13)和问题(18)~(19)的弱形式和离散格式,需要引入下面的Sobolev空间.对于R1=0的情况,定义通常的带权Sobolev空间 相应的内积和范数分别为 其中ω=1+t是权函数.引入带权Sobolev空间 相应的内积和范数分别为: 其中 对于R1>0的情况,定义Sobolev空间 相应的内积和范数为 进一步,引入Sobolev空间 相应的内积和范数分别为: 其中 本节证明逼近特征值和特征向量的误差估计.为了简洁起见,仅对R1>0的情况给出证明,R1=0的情况可以类似推导.用ab表示a≤Mb,其中M为独立于N且大于零的常数. 证明由于-1 2R1 从而 由Cauchy-Schwarz不等式有 从而有 am(um,um)|um||um.】 类似于定理1的证明,有下面结论. 定理2bm(um,vm)是定义在L2(D)×L2(D)上的正定连续的双线性泛函,即 引理1令Γ和ΓN分别为(24)式和(26)式定义的有界线性算子,则ΓN=ΠNΓ. 取vmN=ΠNΓum-ΓNum,并将其代入(29)式可得 am(ΠNΓum-ΓNum,ΠNΓum-ΓNum)=0. 由定理1有ΓN=ΠNΓ.】 引理2设(λm,um)和(λmN,umN)分别为问题(21)和(23)的特征对,则 证明由问题(21)和(23)有 两边同时除以bm(umN,umN)可得(30)式.】 令 证明根据算子范数的定义,可以得到 设R(λm)和R(λmN)分别是问题(21)和(23)的特征值λm和λmN相应的特征函数空间. 定理4设(λm,um)和(λmN,umN)分别为问题(21)和(23)的特征对,则下列不等式成立: ||um-umN||am≤M||(Γ-ΓN)|R(λm)||am.(35) 对于um∈R(λm),||um||am=1,我们有 由上面两个等式及(35)式可得(33)式. 令umN∈R(λmN),||umN||am=1,则 由引理2可得 结合(33)式可得(34)式.】 对于α≤-1,β≤-1的情况,函数ωα,β(x)不在L1(I)中,因此它不能用作一般的权函数.在经典的Jacobi多项式中,权函数的指数α,β>-1.为了应用方便,将经典的Jacobi多项式中权函数的指数α,β中的一个或两个扩展为整数是很有必要的.因此,根据文献[16]的思想,定义带整数指数对(l,k)的广义Jacobi多项式 其中n0≤n,且 定义d维Jacobi多项式的张量和权函数分别为 定义2维N次多项式空间: 引入非一致带权Sobolev空间 其半范数和范数分别为 由文献[17]中的定理8.1和注记8.14,有下面结果. 证明根据定理1和(28)式,有 由定理1知,||um-ΠNum||1,D||um-ΠNum||am,所以 从而 ||um-ΠNum||am||um-vmN||1,D. 由vmN的任意性,有 由Poincaré不等式可得 又由于 所以 再由引理3可知 结合文献[17]中的(3.5.32)式可知(36)式和(37)式成立.】 为了有效地求解问题(22)和(23),首先构造逼近空间中一组适当的基函数,即 其中Li是i次Legendre多项式.因此 令 当R1=0,m=0时,令 当R1=0,m≥1时,令 (40) 对于R1>0的情形,令 其中 由Legendre多项式的正交性可知,(39),(41)和(43)式中的刚度矩阵和质量矩阵都是稀疏矩阵. 为了验证算法的有效性和高精度,在MATLAB 2016a平台上进行数值模拟. 例1取R1=0,R2=1,β=1,m=0,1.对于不同的m和N,表1和表2分别列出了前4个特征值的数值结果. 表1 当m=0时,对应不同N的前4个特征值 表2 当m=1时,对应不同N的前4个特征值 例2取R1=1,R2=2,β=1,m=0,1.对于不同的m和N,表3和表4列出了前4个特征值的数值结果. 总之,数值模拟实验结果说明,文中算法是有效的,并且具有很高的精度. 图1 数值解与参考解的误差 表3 当m=0时,对应不同N的前4个特征值 表4 当m=0时,对应不同N的前4个特征值 图2 数值解与参考解的误差
2 弱形式和离散格式
3 误差估计







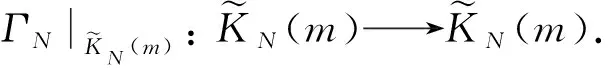




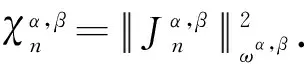







4 算法的有效实现




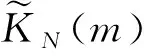
5 数值实验








