阻尼板振动复模态可控性和可观性研究

2022-03-11刘江黎胜

哈尔滨工程大学学报 2022年2期

刘江，黎胜

(1.大连理工大学工业装备结构分析国家重点实验室，辽宁大连 116024； 2.大连理工大学船舶工程学院，辽宁大连 116024)

振动主动控制是振动工程研究领域中的热点之一，其工作原理是通过自动修改结构响应来减小结构的振动。振动主动控制系统的形式多种多样，但是任何此类系统都包含传感器、控制器和作动器[1]，显然，传感器和作动器的布置关系到振动主动控制系统的控制效果，应尽量避免布置在结构振动不可控和不可观位置。结构振动模态的可控性和可观性定义为：安装在振动结构上的作动器能够激起结构的所有模态则此振动结构是可控的；安装在振动结构上的传感器能够检测到结构的所有模态则此振动结构是可观测的[2]。因此，结构振动的可控性和可观性对振动主动控制系统传感器/作动器的布置具有重要意义。

目前对结构振动主动控制中可控性和可观性问题的研究有：Balas等[3]研究了无阻尼和轻阻尼柔性结构的可控性和可观性。Wu等[4]指出，对于柔性结构，传感器和作动器的配置与可控性和可观性有关。黎胜等[5]对结构振动和声辐射可控性和可观性指标进行了研究，提出了基于声压输出的振动模态可观性指标，并且在振动模态可控性和可观性基础上，结合振动模态的声辐射效率，提出了结构声辐射的可控性和可观性指标和基于声压输出的可观性指标。但是，上述研究都是基于实模态展开的，而且对于实模态来说，各阶振动模态节点位置都是该阶模态不可控和不可观位置。而实际的结构振动不可避免的会受到阻尼或者流体加载等因素的影响，都是以复模态的形式存在[6]。

复模态与实模态的区别主要在于：1) 复模态不存在各点位移均为零的瞬间；2) 各点位移之间的比值随时间变化；3) 一般不具有实模态振型所具有的那种稳定的节点或节线[7]。这就导致在可控性和可观性研究时，基于实模态理论的分析就会与结构的实际可控性和可观性产生偏差，从而导致主动控制系统的控制效果减弱。因此基于复模态的阻尼板可控性和可观性研究具有重要的意义。目前可用于结构振动复模态可控性和可观性的研究有：Hamdan等[8]提出了一阶阻尼振动系统(控制方程)的可控性和可观性指标，并且证明了所提出的指标可以直接应用于二阶阻尼振动系统(阻尼系统运动方程)。Yang[9]研究了具有阻尼、陀螺和循环力共同作用的一般机械结构的可控性和可观性，利用与运动方程相关的非正交特征向量来表示系统的传递函数，通过研究传递函数的行和列的线性无关性，得到了模态可控性和可观性条件。

本文对文献[8]提出的可控性和可观性指标进行探讨，论证了其用于复模态的可控性和可观性分析的可行性。基于实模态和复模态理论，以阻尼板结构为例对其模态可控性和可观性指标进行了计算分析，研究了复模态与实模态可控性和可观性的差别。对不同构型阻尼板的复模态复杂度进行计算并探讨了复杂度与复模态可控性和可观性指标的关系，从可控性和可观性角度阐释了实模态和复模态的区别。

1 复模态可控性(可观性)指标

振动控制理论中控制方程常表示为：

(1)

式中：A、B、C分别被称作系统矩阵、输入矩阵、输出矩阵;x为系统响应向量(位移、速度等)；u为外部激励力向量。为了方便描述，上述矩阵设置为：A2n×2n,B2n×m，Cm×2n,um×1。

基于式(1)的控制方程及其特征值问题的求解结果，对系统的可控性和可观性，Kailath等[10]提出了著名的PBH检验准则，准则有PBH特征向量检验和PBH秩检验2种表示方式。Hamdan等[8]将PBH检验推广到了二阶振动方程情况，并基于PBH特征向量检验提出了可控性和可观性指标。

振动方程与式(1)所示的控制方程是同一方程的不同形式，二阶振动方程常表示为：

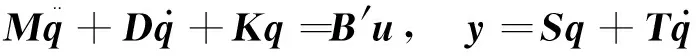
(2)

1) 在j阶控制力情况下，i阶模态是不可控的充分必要条件是：

(3)

2) 在k阶测量输出情况下，l阶模态是不可观的充分必要条件是：

(4)

式中wl为第l个特征值对应的右特征向量；sk、tk分别为输出矩阵S、T的第k列。基于上述特征向量检验，文献[8]给出了二阶振动方程的可控性和可观性指标：

(5)

式中：θij为控制力位置向量b′j和左特征向量vi夹角；φkl为输出位置向量sk+λltk和右特征向量wl夹角。可控性或可观性越好上述指标值越大，指标为0的位置不可控或不可观。

当上述指标用在振动实模态的可控性和可观性研究时，各阶振动模态的节点位置指标值恒为0，也就是说在振动实模态的可控性和可观性研究中，节点位置是完全不可控和不可观的位置。而振动复模态相比于实模态不存在固定节点，由此推测复模态的可控性和可观性与实模态可能存在明显的区别。通过上述分析可知，式(5)的可控性和可观性指标是由式(2)所示的振动方程的特征向量与输入输出矩阵列向量的夹角表示，而且，式(2)包含阻尼矩阵信息，即其振动模态求解结果为复模态。所以本文认为，式(5)所示的可控性和可观性指标可以用于振动复模态可控性和可观性分析。

2 复模态对可控性和可观性的影响

2.1 实模态和复模态结构模型

为了得到实模态和复模态，建立了如图1(a)所示的均匀阻尼板和图1(b)所示的非均匀阻尼板有限元模型：板长Lx=0.455 m，板宽Ly=0.379 m，板厚h=0.003 m，板密度ρ=7 850 kg/m3，杨氏模量E=2.1×1011N/m2，泊松比υ=0.3，边界条件是四边简支。Rayleigh阻尼模型被广泛用于商业有限元软件中的阻尼结构的模态分析，且本文结果与阻尼模型无关，因此用该模型定义结构的阻尼。

图1 阻尼板有限元模型及输入(输出)位置Fig.1 FE-model of damped plates and positions of input (output)

对于非均匀阻尼板，通过在不同区域设置不同阻尼比来建立，浅色和深色区域阻尼比分别为ξ1和ξ2。阻尼矩阵D表示为质量矩阵M和刚度矩阵K的线性组合。在结构不同区域设置不同的阻尼比，其阻尼矩阵可以表示为：

(6)

式中：N为阻尼区域的数量；Mi和Ki为第i个区域结构的质量阵和刚度阵；αi和βi为第i个区域的Rayleigh阻尼比例系数。假定第i个区域的期望阻尼比值为ξi，则比例系数可表示为：

(7)

式中ω1和ω2为结构任意两阶固有频率。

在上述有限元模型中，浅色区域代表纯钢板部分，ξ1=0.01，深色区域代表高阻尼部分，ξ2=0.2。模型网格划分采用ANSYS®SHELL181单元，有限元网格为40×24，共有960个单元，1 025个节点[13]。利用DAMP模态求解器对均匀阻尼板R和非均匀阻尼板C2进行模态分析，得到其前五阶振动模态，模态阶数表示为a×b，a和b分别表示板长和板宽方向的波数。图2给出了R板和C2板2×2和3×1阶振动模态幅值和相位分布。

从图中可以看出，由于阻尼的非均匀设置，结构的模态振型发生改变，尤其是相位的改变尤为突出，这也是复模态相较于实模态显著的特点，结构的各个位置不再同时达到最大值、最小值或同时经过平衡位置。

2.2 实模态与复模态可控性(可观性)对比

选取图1(c)中所示的12个点作为板上用于输入(主动控制的控制力)和输出(振动响应测量)的位置，将实模态(R)和复模态(C2)的模态分析结果代入式(5)，分别计算其在12个点上前5阶模态的模态可控性(可观性)指标。图3给出了实模态和复模态可控性(可观性)对比结果，实线图标代表实模态，虚线图标代表复模态。需要说明的是图3中的可观性指标计算只考虑了振动位移测量输出，对同一位置其模态可观性和可控性指标是一样的，即cosθ=cosφ。

从图3中可以看出，对于实模态：位置1-12对1×1和3×1阶模态都具有较好的可控性(可观性)，位置2、5和9对2×1阶模态是不可控(不可观)的，位置4、5和6对1×2模态是不可控(不可观)的，位置2、4、5、6和9对2×2阶模态是不可控(不可观)的；复模态与实模态有所不同：对于1×1，2×1，1×2阶模态，复模态可控性和可观性指标与实模态基本相同；对于2×2，3×1阶模态，复模态可控性和可观性指标与实模态明显不同，且对于不同位置指标值有的增大有的减小。

综上所述，在相同阶模态和相同输入(输出)位置，实模态情况下的与复模态情况下模态可控性(可观性)不同。

3 复杂度对可控性和可观性的影响

3.1 复模态复杂度计算

目前常用的量化模态复杂度的参数有平均相位偏差MPD，模态相关系数MCC，模态相位共线性系数MPC，模态复杂度因子MCF(MCF1、MCF2、MCF3)，模态复杂度指标MSC[14]。本文主要通过模态分析得到阻尼板的振型数据进行计算分析，而MPD是由复振型的幅值和相位来量化模态复杂度的参数，因此选取MPD来量化不同构型板结构的模态复杂度。平均相位偏差(mean phase deviation，MPD)常表示为：

(8)

非均匀阻尼板高阻尼区域的分布情况会影响复模态的复杂程度，本文参考文献[15]中定义的阻尼构型，根据对称性和几何分布的不同，构建图4所示的8种构型。其中，S为对称型，B为左右对称型，C为中心对称型，A为不对称型，1、2是根据距离板中心和边界的距离分别代表集中分散。有限元模型设置与2.1节一致，对8种不同构型的非均匀阻尼板进行模态分析，并代入式(8)计算其MPD值，计算结果如表1所示。

图4 8种阻尼板构型Fig.4 8 configurations of damped plates

从表1可以看出，在 2×2和3×1阶模态C2的复模态复杂度较高，在1×1、2×1和1×2阶模态C2的复模态复杂度较低。结合图3可以看出，在2×2和3×1阶模态C2与R的可控性和可观性指标存在明显差异，在1×1、2×1和1×2阶模态C2与R的可控性和可观性指标基本相同。由此可知，在模态可控性和可观性方面复模态相比于实模态的变化量与复模态复杂度有关。

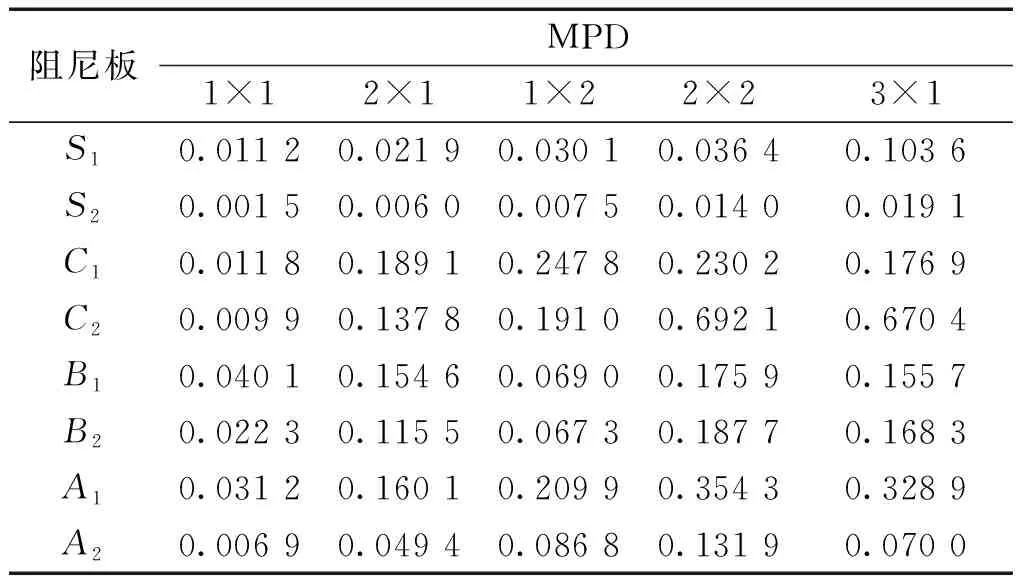
表1 8种阻尼板前5阶MPD值Table 1 MPDs for 8 damped plates from 1st to 5th mode

3.2 可控性(可观性)计算对比

为了研究模态复杂度对复模态可控性(可观性)的影响，将8种阻尼板的前5阶模态的可控性(可观性)指标，分别按照MPD由小到大的顺序重新整理，图5～9分别为前5阶模态不同构型的非均匀阻尼板(不同复杂度)，12个输入(输出)位置处的可控性(可观性)指标与均匀阻尼板R的对比结果，其中，括号内的数字代表该构型在这阶模态下的复杂度MPD值。

图5 1×1阶不同复杂度板可控性(可观性)对比Fig.5 Comparison of controllability (observability) for damped plates with different complexities on 1×1 mode

图6 2×1阶不同复杂度板可控性(可观性)对比Fig.6 Comparison of controllability (observability) for damped plates with different complexities on 2×1 mode

图7 1×2阶不同复杂度板可控性(可观性)对比Fig.7 Comparison of controllability (observability) for damped plates with different complexities on 1×2 mode

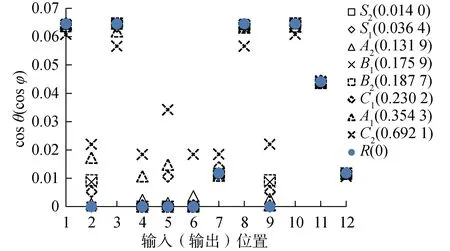
图8 2×2阶不同复杂度板可控性(可观性)对比Fig.8 Comparison of controllability (observability) for damped plates with different complexities on 2×2 mode

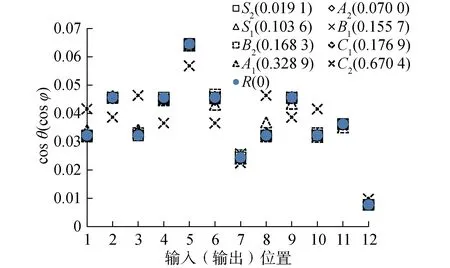
图9 3×1阶不同复杂度板可控性(可观性)对比Fig.9 Comparison of controllability (observability) for damped plates with different complexities on 3×1 mode

由图5～9可知，不同模态复杂度MPD值的阻尼板的可控性(可观性)相比于复杂度MPD=0(实模态)的阻尼板变化可以分为3种情况：1) 当MPD<0.1时，或当0.10.3或0.10.3且输入(输出)点不在均匀阻尼板R实模态振型的节点位置时，可控性(可观性)降低。综上所述，复模态的模态复杂度对其可控性和可观性的有影响，具体是对可控性和可观性增强、降低还是不变，取决于所关心的输入和输出位置。

不可控和不可观的位置(可控性(可观性)指标为0)为输入和输出应该尽量避免的位置点。由图5～9可知，均匀阻尼板R(实模态)存在不可控和不可观点：2×1阶模态的2、5、9号点；1×2阶模态的4、5、6号点；2×2阶模态的2、4、5、6、9号点。为了研究复模态复杂度对上述不可控和不可观点的影响，计算了8种非均匀阻尼板2×1阶模态的2、5、9号点，1×2 阶模态的4、5、6号点以及2×2阶模态的2、4、5、6、9号点的可控性和可观性指标平均值，并绘制平均值随复模态复杂度变化图，如图10所示。

图10 复杂度对指标平均值影响Fig.10 Influence of complexity on averagecosθs

由图10可知，实模态情况下不可控和不可观的点的可控性(可观性)指标平均值随着复模态的模态复杂度的增大呈增大趋势，且其分布接近线性增长。因此，对3种模态下的计算结果进行线性拟合得到图10中y所示拟合曲线。文献[5]中认为，可控性(可观性)指标cosθ(cosφ)<0.01时，该点对于该阶模态而言是不可控(不可观)的。通过拟合曲线y=0.034 4x-0.002 1可知，当MPD值小于0.351 7时，cosθ(cosφ)平均值均小于0.01。因此，在本文所研究算例下，从可控性和可观性的角度去考虑复模态与实模态的区别时，当MPD<0.357 1时，复模态可简化为实模态进行可控性(可观性)的分析；当MPD>0.357 1时，复模态不能近似为实模态进行可控性(可观性)分析。

综上所述，本文认为，任意以复模态形式振动的结构，从可控性和可观性的角度去考虑复模态与实模态的区别时，都满足如下规律：当复模态的模态复杂度小于某一值时，复模态可简化为实模态进行可控性和可观性的分析；当复模态的模态复杂度大于某一值时，会对可控性和可观性产生较大的影响，此时复模态不能近似为实模态进行可控性和可观性分析。