长杆弹超高速侵彻砂浆靶临界速度的实验和计算

姚志彦， 李金柱， 齐凯丽， 徐杨， 黄风雷

(北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081)

0 引言

随着现代防御体系的发展，重要军事目标的混凝土掩体的厚度也在增加。为了有效地打击此类坚固的军事目标，各国都在发展基于超高速发射平台(4～5 Ma)的动能武器。杆式动能弹作为超高速动能武器的一种，对目标的破坏方式是通过弹体撞击目标时的动能对目标进行侵彻；并且，随着撞击速度的增加，侵彻深度增加。然而，当侵彻速度增加到某一临界值时，侵彻深度不再随撞击速度的增加而增加，反而减小。为了充分发挥动能弹的侵彻能力，有必要研究侵彻深度逆减的临界速度。高飞等开展了卵形30CrMnSiNi2A动能弹在1 225～2 392 m/s速度范围内侵彻41.8 MPa砂浆混凝土靶的实验，得到了侵彻深度逆减的转变速度为1 720 m/s。Gold等进行了直径为1.3 cm长径比为14.5的铜杆和钽杆以速度1 500～1 900 m/s侵彻半无限厚混凝土靶的实验，发现当弹体强度增大时，侵彻深度会增加，并且存在一个临界速度，当侵彻速度超过该临界速度时，侵彻深度随着速度的增加反而会减小。练兵等进行了钨合金动能杆以速度1 218～1 863 m/s侵彻强度为35 MPa半无限混凝土靶板的实验，实验中当速度为1 518 m/s时侵彻深度最大，当速度大于1 518 m/s时侵彻深度减小，并进行了相关的数值模拟工作。宋梅利等开展了两组不同强度和尺寸的30CrMnSiNi2A弹体以速度880～1 900 m/s侵彻40 MPa半无限厚素混凝土靶的实验，结果表明：弹体的侵彻深度先增大后减小，存在侵彻深度最大时的临界速度，并且随着弹体强度的增加，弹体的侵彻深度增加。Davis等通过实验发现，随着撞击速度的增大，弹体头部变形严重，头部会发生镦粗，侵彻深度随着初速度的增加出现了先增加后减小的现象。Liu等开展了中碳钢平头长杆弹以速度500～1 800 m/s侵彻强度为50 MPa半无限厚砂浆混凝土靶的实验，并基于实验结果分别建立了刚性侵彻、侵蚀侵彻和流体侵彻模型。Kong等进行了平头钢质弹丸以速度510～1 850 m/s侵彻混凝土砂浆的实验，以空腔膨胀理论为基础，建立了刚性侵彻和侵蚀侵彻模型，但对侵蚀侵彻阶段没有深入的讨论。Chen等给出了弹体从刚性侵彻转变到半流体侵彻的临界条件以及刚性侵彻的上限和流体侵彻的下限。Rosenberg等考虑到侵彻过程中的“蘑菇头”变形，基于力平衡引入了“有效横截面积”对A-T模型进行修正。Wang等通过引入工程应变对A-T模型进行修正。刘闯等基于弹体的质量守恒、动量守恒和动态强度计算方法确定了半球头长杆弹超高速侵彻过程中的临界速度，但是对于侵彻过程靶板的动态强度未做深入的考虑。王可慧等进行了高速弹体非正侵彻混凝土靶板的弹道偏转研究，发现高速侵彻时侵彻弹道的偏转效应相较于较低速侵彻时更为明显。钱秉文等、陈海华等、宋春明等也相继开展了长杆弹超高速侵彻的实验和理论方面的工作。综上所述，针对长杆弹超高速侵彻混凝土靶方面的问题，前人已在理论建模、实验研究和数值模拟方面开展了较多的研究，但对于弹道偏转、弹体变形等机理仍然需要进一步解释说明；对于侵彻过程中的侵彻深度发生逆减的临界速度也需要结合弹体和靶板的动态强度以及弹体头部的镦粗变形给出解析模型。

基于上述研究现状，本文开展了直径4 mm、长度32 mm、长径比8的30CrMnSiNi2A高强度合金钢尖卵形长杆弹在1 381～1 879 m/s速度范围内侵彻强度为39.5 MPa砂浆混凝土靶板的实验。基于实验结果和理论模型，解释了长杆弹超高速侵彻砂浆混凝土靶时深度变化规律和侵彻弹道失稳机理，在考虑长杆弹侵彻过程中弹体和靶板的动态强度以及弹体头部的镦粗变形的基础上给出了侵彻深度发生逆减的临界速度模型。

1 实验方案

1.1 弹体参数

长杆弹的材料采用30CrMnSiNi2A高强度合金钢，其力学性能如表1所示。根据实验目的和二级轻气炮的发射能力，长杆弹设计如下：弹体直径为4 mm、长度为32 mm、长径比为8、头部形状为尖卵形、CRH为3、初始质量为2.86 g。长杆弹的结构图和实物图如图1所示。因为轻气炮的口径大于长杆弹的直径，设计弹托来满足次口径发射，弹和弹托之间利用能承受较大单向剪切应力的锯齿形螺纹连接，弹托的设计采用杯状弹托，弹托的结构和尺寸以及弹托装配如图2所示。

表1 30CrMnSiNi2A材料的力学性能

图1 长杆弹结构图和实物图Fig.1 Dimensions and photograph of long-rod projectile

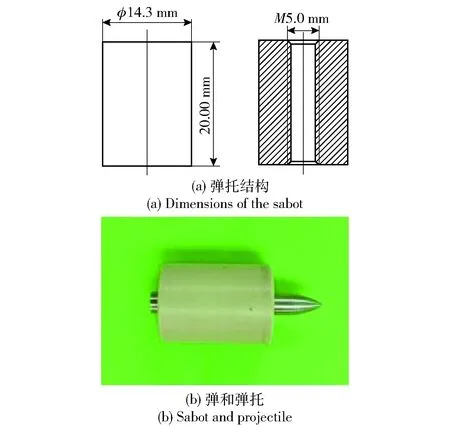
图2 弹托结构以及弹和弹托组装Fig.2 Sabot structure and the image of projectile and sabot

1.2 靶板设计

实验中为了消除骨料和边界效应对实验结果的影响，设计靶板为直径400 mm(100倍弹径)、高400 mm的圆柱形砂浆混凝土靶，外层用4 mm厚钢板围箍，如图3所示。在浇筑靶板的同时也浇筑了3个100 mm×100 mm×100 mm的砂浆混凝土试件，将靶板和试件在同样的环境下养护28 d。养护完成后对试件进行单轴压缩实验，并得到了三组试件的应力- 应变曲线，如图4所示。根据《混凝土强度检验评定标准》规定以及放置日期和强度的关系，最终实验的砂浆混凝土靶的强度为39.5 MPa。

图3 实验用砂浆混凝土靶Fig.3 Photograph of the mortar concrete target

图4 应力- 应变曲线Fig.4 Stress-strain curve

1.3 测试系统

利用口径为14.5 mm的二级轻气炮作为发射装置，示意图如图5所示，主要由高压气室、一级炮管、锥段、二级炮管、弹托分离室、测速装置和靶室构成。工作过程为：高压气体推动活塞运动，对一级炮管中的气体进行压缩，当气体的压力达到一定值时，锥段处的膜片发生破裂，气体推动杆弹和弹托进行加速。长杆弹的速度通过固定磁体感应测速的方法来获得，装置中有三组磁环和线圈，当长杆弹穿过磁环时线圈中产生的感应电流被示波器捕捉，三个磁环的间距已知，长杆弹飞行的时间通过示波器获得，因此长杆弹的速度可以通过三个速度求平均得到，图6是测速装置示意图和典型的速度信号。实验中长杆弹的飞行姿态通过放置在靶室窗口的高速摄影装置拍摄获取，长杆弹在不同速度下着靶姿态，如图7所示，从中可以看出部分弹体在着靶时有微小倾角。

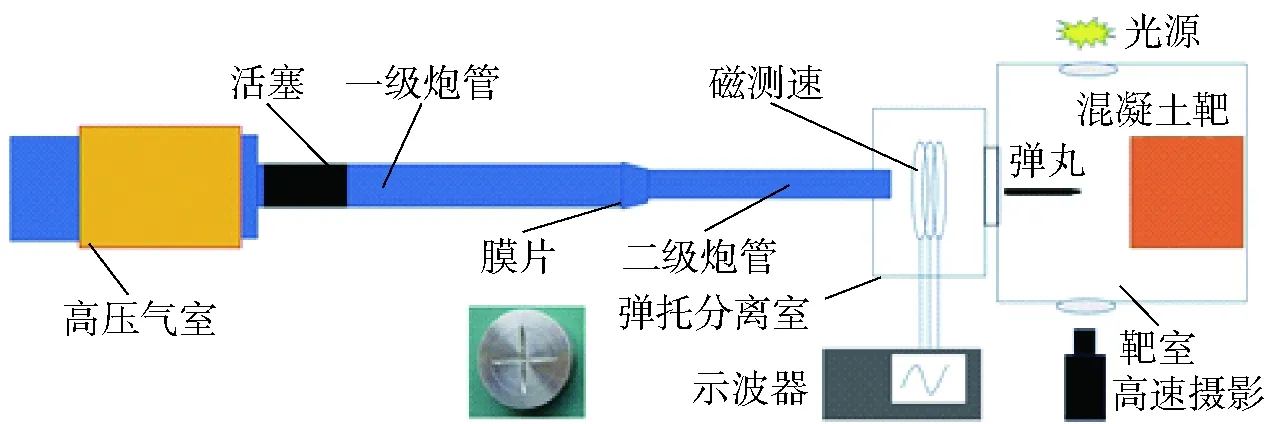
图5 二级轻气炮示意图Fig.5 Schematicofthe two-stage light gas gun

图6 磁测速装置示意图和典型的速度信号Fig.6 Schematic of velocimeter and typical velocity signal

图7 不同速度下长杆弹着靶姿态Fig.7 Hitting attitudes of the long-rod projectile at different velocities

2 实验结果及分析

本文开展了直径4 mm、长度32 mm、长径比8的30CrMnSiNi2A高强度合金钢尖卵形长杆弹以1 381～1 879 m/s速度范围侵彻砂浆混凝土靶板的实验。实验结束后测量并记录了靶板的侵彻深度(DOP)、开坑直径()、开坑深度()、弹洞直径()、侵彻弹道的形貌以及长杆弹剩余质量()和剩余长度()等数据。

2.1 长杆弹回收形态

实验后将长杆弹进行回收，如表2所示。从表2中可以看出弹体表面有明显的磨蚀，弹头变钝，弹体变短，弹体表面附着一层砂浆。剔除弹体表面的砂浆后进行称重并测量剩余长度，具体数据如表3所示。由于第2号实验弹体未有效回收，故未给出其相关数据。从表2和表3可以看出，当<1 724 m/s时，弹体的质量损失最大为3.49%，弹体除了头部变钝和表层磨蚀之外无弯曲变形。当≥1 724 m/s时，弹体的质量损失大于10%，最大为25.87%，弹体的头部变钝，表层磨蚀严重，弹体发生了弯曲变形。

表2 实验前后弹体对比

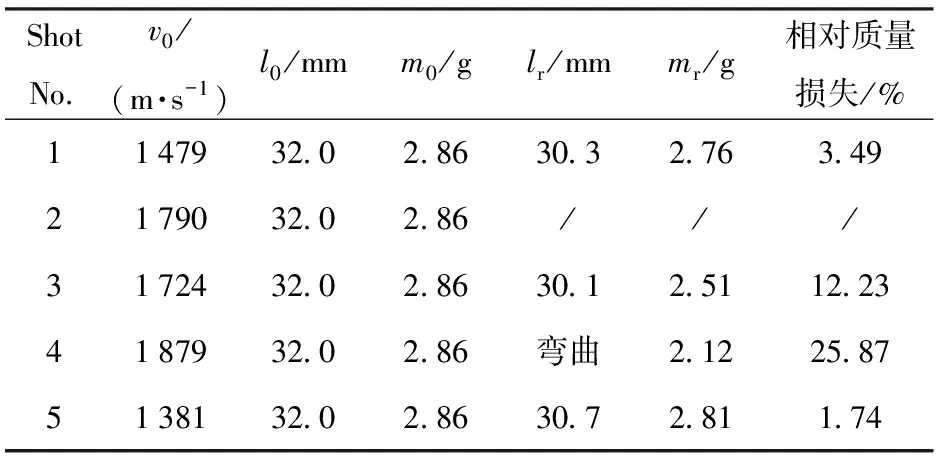
表3 实验后弹体数据

上述弹体质量损失的实验现象可以解释为：当<1 724 m/s时，弹体在侵彻过程中与靶板之间的剧烈摩擦使得弹体的质量减小。当≥1 724 m/s时，弹体与靶板之间的瞬态高压导致弹体材料发生塑性变形的塑性功大部分转化为热能，使弹体外表面薄层发生热软化，热软化的部分在侵彻过程中被剥离。而长杆弹在侵彻过程中发生弯曲变形，是因为在超高速侵彻过程中弹靶接触面之间的高压导致弹头发生的镦粗变形以及砂浆混凝土介质的不均匀性共同作用，使得长杆弹受力不对称，在横向弯矩的作用下发生弯曲。

2.2 靶板破坏情况

图8给出了不同速度下实验后靶板的破坏情况，靶板的破坏由三部分组成，分别是表层崩落、正面开坑破坏以及侵彻弹道。长杆弹的弹托在飞行过程中发生破碎，破碎后的碎块飞射到靶面使得靶板出现了表层崩落现象。正面开坑破坏是因为当长杆弹以超高速撞击靶板时，在碰撞界面产生极高的压力，并分别向弹体和靶板传播两个冲击波。向靶板内部传播的冲击波一部分向靶板的背表面方向传播，另一部分由于靶板正面的自由面效应发生卸载，产生拉伸波。拉伸波产生的应力幅值大于靶板的抗拉强度，靶板材料发生拉伸破坏，向外飞溅，使得靶板正面形成了漏斗坑。靶板产生开坑破坏后弹体的剩余动能依然很高，弹体将继续和靶板作用，在这个过程中弹体和靶板发生挤压效应。通过挤压效应，弹体将动能传递给靶板，使得靶板形成弹洞并向外扩张形成了侵彻弹道。

图8 靶板正面破坏Fig.8 Frontal damage of the target

由于弹托在着靶前未完全与弹体分离开而撞击在靶板上，使得靶板的实际开坑面积比无弹托时弹体撞击的开坑面积更大。综合高速摄影和靶板正面破坏情况可以看到，弹托在飞行过程中未破碎时，靶板表面的开坑破坏更为集中，接近于“圆形漏斗”开坑。而当弹托在飞行过程中破碎时，靶板表面的开坑破坏形状不规则，这是弹托破碎的部分撞击到靶板表面导致的。

实验后对靶板的开坑破坏等情况进行了测量，表4给出了不同撞击速度下靶板的侵彻深度()、开坑直径()、开坑深度()、弹道孔径()和开坑体积()。其中，开坑直径()的值为测量多个方向后的平均值，测量情况如图9所示；开坑体积()通过填砂获得。图10给出了开坑直径()、开坑深度()、开坑体积()和无量纲弹道孔径()与侵彻速度()的拟合关系，从中可以看出、、和与近似呈正比关系，但离散程度较大。

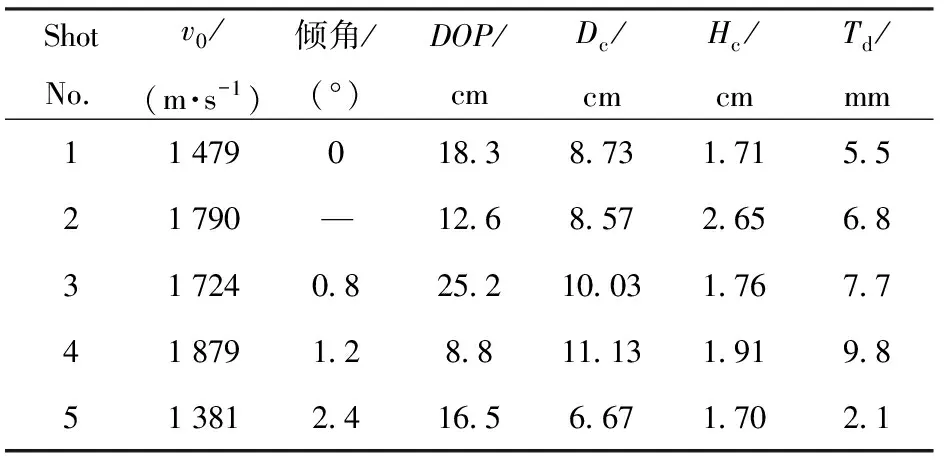
表4 实验后靶板数据

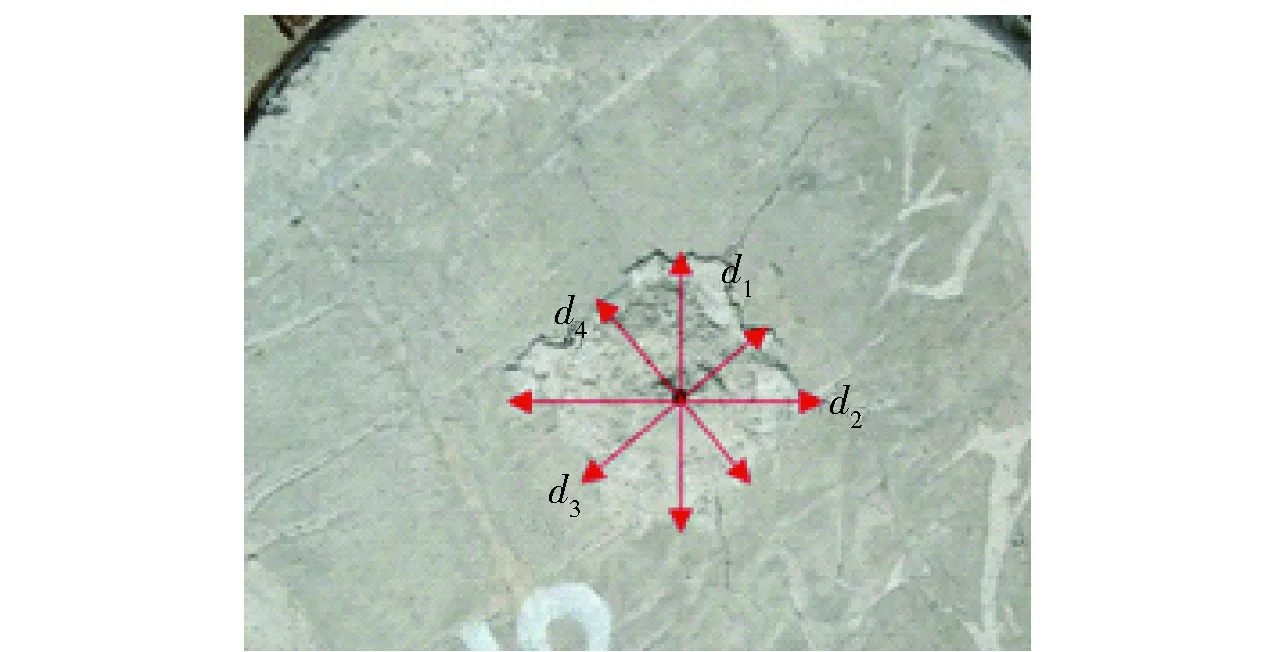
图9 开坑直径的测量Fig.9 Measurements of the crater diameter

图10 开坑直径、开坑深度、开坑体积、无量纲弹洞孔径与速度的关系Fig.10 Crater diameter、 Crater depth、 Crater volume、 Dimensionless ballistic aperture versus velocity

2.3 侵彻弹道分析

对侵彻后的靶板进行剖分，得到了不同侵彻速度下的侵彻弹道，如图11所示。图11中，为靶面法向方向。不同速度下的侵彻弹道的形貌不同。如图11(a)所示，当为1 381 m/s时，侵彻弹道发生了偏转，从图7(a)的高速摄影也可以观察到长杆弹着靶时有微小的倾角。当为1 479 m/s时，长杆弹着靶时姿态垂直于靶面，侵彻弹道未发生偏转。当为1 724 m/s时，侵彻弹道的前半部分偏转较小，后半部分弹道偏转明显增大，并且相较于图11(a)的侵彻弹道发生了更大的偏转，然而对比图7(a)和图7(c)可以看到当为1 724 m/s时长杆弹着靶时的倾角更小，因此图11(c)的后半部分弹道偏转更加严重的原因不是长杆弹着靶时的微小倾角，而是长杆弹在侵彻过程中弹体头部处于高压、高温状态而发生变形，弹体头部受力不对称，使得弹体的运动方向发生了改变。当为1 879 m/s的侵彻弹道和靶板正面法线方向也存在夹角，且弹道先向左偏转后向右偏转，向左偏转是因为着靶姿态非垂直于靶面，向右偏转是由于弹体发生了侵蚀和弯曲变形，受力状态发生了改变。

图11 不同速度下的侵彻弹道Fig.11 Penetration trajectories at different velocities

长杆弹在超高速侵彻中的着靶姿态的微小倾角和弹体变形会使得侵彻弹道发生失稳，其形状近似为“J”字形弹道。根据上述非正侵彻的侵彻弹道形貌，可以将非正侵彻过程分为三段，如图12所示，分别为：段，开坑段，在此阶段靶面混凝土破碎向后飞散，弹体无横向力作用，弹体的姿态不变；段，准直线段，在此阶段，弹体开始进入靶板，并与靶板发生挤压作用，弹体处于高压高温状态，同时由于靶板介质的不均匀性，使得弹体头部受力不对称，弹体开始发生变形，但是侵彻弹道尚未发生较大的偏转；段，弯曲段，弹体在段的变形累计加剧导致弹体的受力不对称性加剧，弹体在运动过程中的转矩增大，进而使得弹体的运动方向发生改变，侵彻弹道发生较大偏转。图12中，′为侵彻弹道最大偏转距离靶面法线的距离。

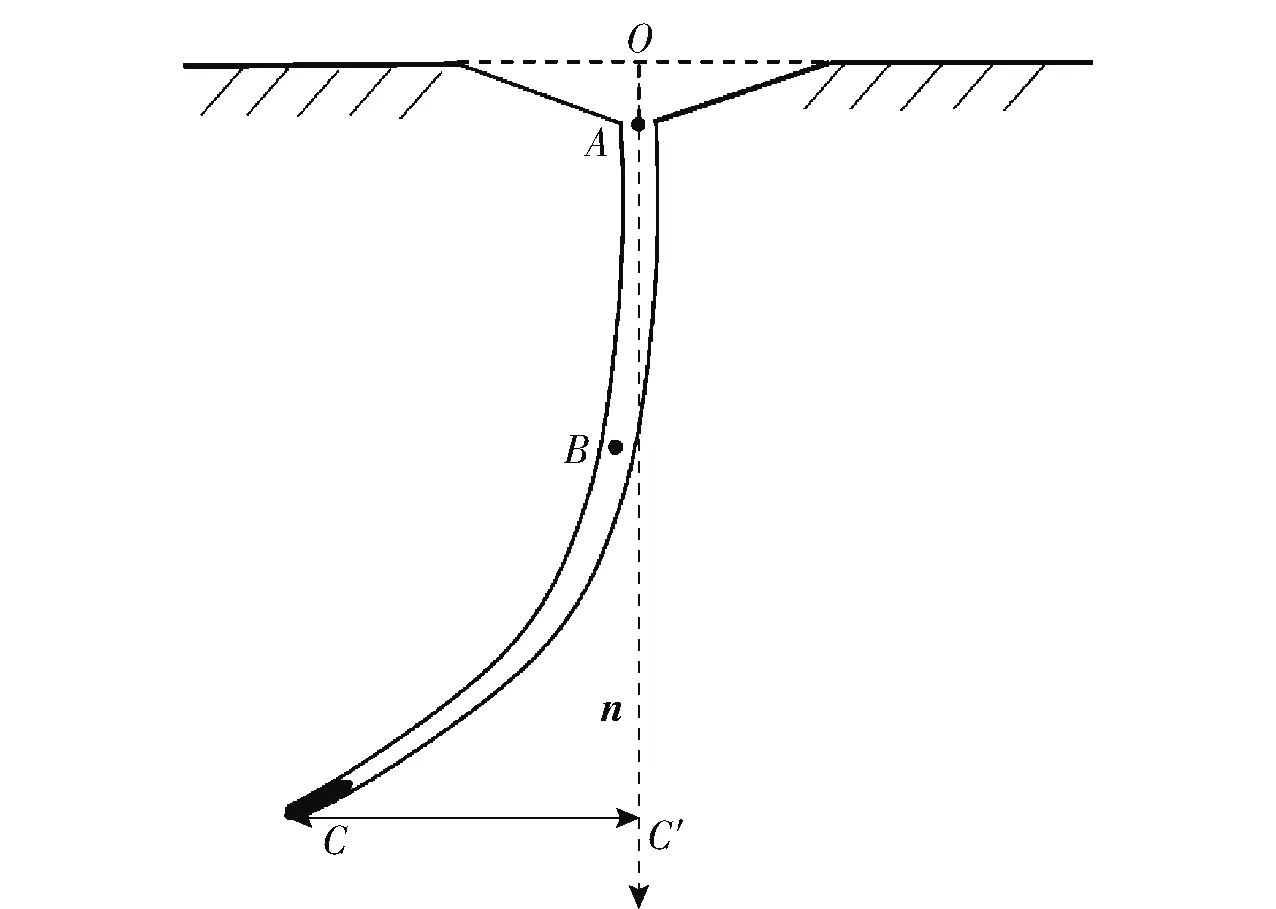
图12 弹道偏转示意图Fig.12 Trajectory deflection diagram

从图11中可以看到，侵彻速度为1 381 m/s和1 724 m/s的侵彻弹道发生了严重偏转，偏转程度如表5所示，为最大偏转距离相较于最大侵彻深度的相对偏转率。从表5中可以看到：当速度为1 381 m/s时，弹体着靶时的倾角为2.4°，侵彻弹道的相对偏转率为16.9%；当速度为1 724 m/s时，弹体着靶时的倾角为0.8°，但是侵彻弹道的相对偏转率为31.3%。上述结果表明弹体的侵彻速度越高，侵彻弹道的不稳定性更加严重，侵彻弹道更容易发生较大偏转。

表5 侵彻弹道偏转程度

2.4 侵彻深度随初速度的变化规律

长杆弹侵彻混凝土靶的侵彻深度随速度的变化关系如图13所示。由图13可以看出：侵彻深度没有随速度的增加一直增加，而是侵彻速度1 724 m/s左右存在一个最大值；当小于1 724 m/s时，侵彻深度随着速度的增加而增加；当大于1 724 m/s时，侵彻深度随着速度的增加减小。

图13 实验无量纲侵彻深度随速度的变化Fig.13 Experimentally dimensionless DOP versus velocity

3 临界速度理论分析

3.1 理论模型

长杆弹在超高速侵彻时弹体头部会发生侵蚀和镦粗变形，并且随着弹体的速度增加，靶板的侵彻深度增加，然而当侵彻速度增加到一定值时，侵彻深度达到最大，若继续提高侵彻速度，则侵彻深度反而会减小。在此，将侵彻深度达到最大时的速度称之为临界速度。为了充分发挥高超声速武器的打击能力，找到侵彻深度逆减的临界速度至关重要。因此，基于实验现象，采用Wang等的理论模型对弹靶接触面上的弹体所受压力进行描述。在考虑长杆弹侵彻过程中弹靶作用和弹体头部镦粗变形的基础上，对传统的A-T模型进行修正，最终给出弹靶接触面的压力关系式。为了方便理论模型的计算，有如下假设：1)长杆弹侵彻靶板时为一维准定常运动；2)弹体在侵彻过程中等效为不可压缩的刚塑性材料；3)靶板底部仅有小部分碎渣堆积，且这部分碎渣的速度为；4)不考虑侵彻过程中的热效应和摩擦效应。基于以上假设，可以对长杆弹高速/超高速侵彻混凝土靶板进行求解。Wang等将A-T模型中的弹体侵蚀率方程、减速方程和弹体头部压力进行修正，给出了弹靶交界面的平衡方程：

(1)

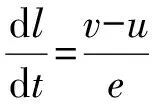
(2)

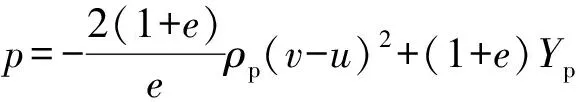
(3)

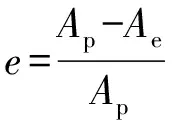
(4)

=(1+)

(5)

式中：为长杆弹弹身的横截面积；为弹体头部发生变形后的等效横截面积；为弹体的强度表征项，为常数，取值为07；为弹体动态屈服强度；为长杆弹的密度；为长杆弹的初始长度；为长杆弹的初始速度；为长杆弹的侵彻速度。为了得到混凝土靶板坑底的压力，在弹靶交界面处建立坐标系，如图14所示，该坐标系以侵彻速度移动。

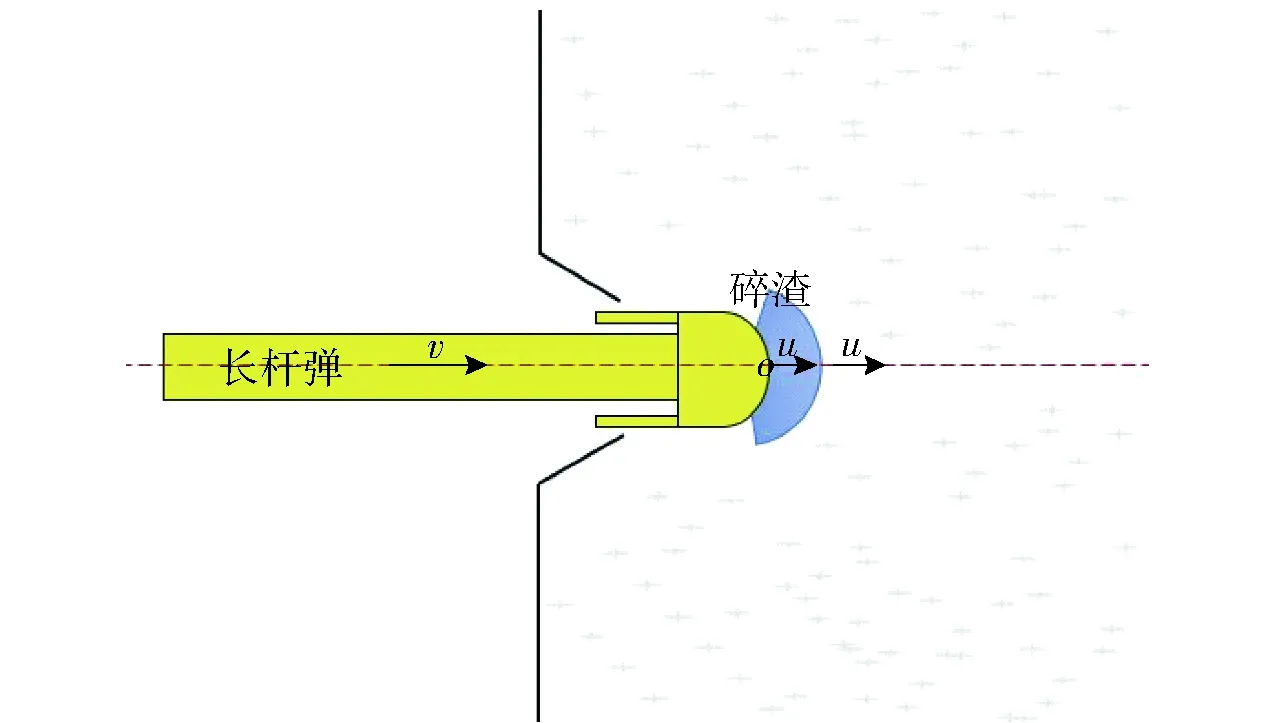
图14 弹体侵彻过程示意图Fig.14 Schematic diagram of the penetration process

假设弹坑底部碎渣的质量为，碎渣等效圆柱体的面积为，弹坑底部流入和流出的碎渣的质量为，则流入和流出的碎渣的动量大小为，通过动量定理可以得到：

(6)

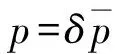
(7)

式中：=,为弹体头部蘑菇头的等效横截面积，其值根据文献[12]近似取05。

在A-T模型中，弹坑底部的压力描述为

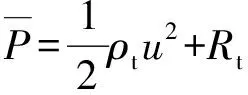
(8)

式中：为混凝土靶的阻力项,本文中的取值形式

(9)

为混凝土靶的杨氏模量；为混凝土靶的动态屈服强度，取值为4倍的静态屈服强度。

根据(3)式、(7)式和(8)式可以得到弹靶交界面处的压力表达式为

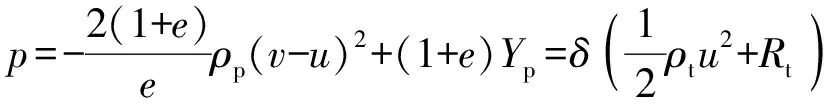
(10)

可以化简为

=(-)+=+

(11)

式中：

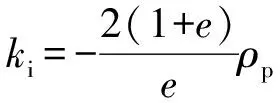
(12)

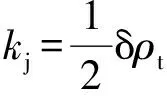
(13)

=(1+)

(14)

=δ

(15)

对(11)式进行求解，可以得到：

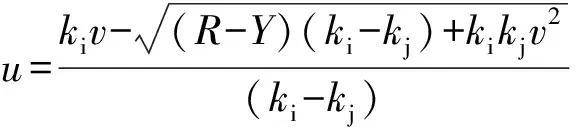
(16)

与A-T模型相似，和的大小会影响侵彻过程，现在对和的相对大小分别进行讨论：

1)<。当<时，令-=0，由 (11)式、(13)式、(14)式和(15)式可得到弹体进入侵蚀侵彻阶段的临界速度为

(17)

2)>。当>时，令=0，此时弹靶接触面的压力=，由(11)式、(12)式、(14)式和(15)式可得弹靶共同发生破坏的临界速度为

(18)

当<时，弹体不能侵入靶板，但是弹体的速度和长度会保持衰减，直至弹体速度为0 m/s。当>时，弹靶共同破坏，弹体能侵入靶板中，但不存在一维准定常运动。在上述侵彻过程中弹靶接触面的压力始终大于弹体的强度，不存在刚性侵彻阶段。

3.2 弹靶参数对临界速度的影响

上述理论分析结果表明，不同的弹靶参数对侵彻深度发生逆减的临界速度有着显著的影响。在此讨论弹体强度和靶板强度对临界速度的影响，如图15所示。从图15中可以看出：靶板强度相同时，临界速度与弹体强度的呈正相关；弹体强度相同时，临界速度与靶板强度呈负相关。因此为了更好地提高侵彻效果，应该增强弹体的强度。

图15 不同弹体和靶板强度的临界速度Fig.15 Critical velocityunder different projectile and target strengths

3.3 临界速度模型可靠性验证

为了验证理论模型的适用性，将本文实验以及练兵等、Liu等、徐晨阳等的弹靶参数代入到理论模型计算，具体参数如表6所示，结果如图16所示。从图16中可以看出，理论模型计算的结果与实验结果基本相符。因此可以认为该理论模型可以较好地预测长杆弹超高速侵彻砂浆混凝土靶时侵彻深度发生逆减的临界速度。

表6 模型计算弹靶参数表

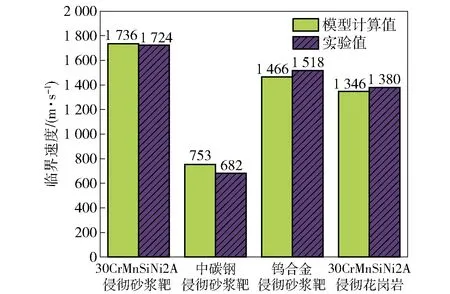
图16 模型计算值和实验值临界速度对比Fig.16 Comparison between model results and literature critical velocity

综上可知，长杆弹超高速侵彻砂浆混凝土靶时侵彻深度不会随着侵彻速度的增加一直增加，而是存在某一临界速度，在该速度处侵彻深度达到峰值，不再增加。本文在考虑弹体侵彻过程中的头部变形基础上对A-T模型进行修正，获得的模型能较好地预测长杆弹超高速侵彻砂浆混凝土时侵彻深度发生逆减的临界速度。

4 结论

本文进行了30CrMnSiNi2A长杆弹在1 381～1 879 m/s的速度范围内侵彻砂浆混凝土靶的实验，并开展了相应的理论分析工作。得到如下主要结论：

1)分析了不同速度下侵彻深度、开坑直径、开坑深度、开坑体积以及开孔直径等破坏情况。实验结果表明，除了侵彻深度外，靶板的开坑直径、开坑深度、开坑体积以及开孔直径与侵彻速度呈近似线性关系，如图10所示。

2)长杆弹超高速侵彻砂浆混凝土靶板时存在侵彻深度发生逆减的临界速度，如图16所示，30CrMnSiNi2A长杆弹侵彻砂浆混凝土靶的临界速度约为1 736 m/s，中碳钢长杆弹侵彻砂浆混凝土靶的临界速度约为753 m/s，钨合金长杆弹侵彻砂浆混凝土靶的临界速度约为1 466 m/s，30CrMnSiNi2A长杆弹侵彻花岗岩的临界速度约为1 359 m/s。

3)长杆弹超高速侵彻砂浆混凝土靶时，其侵彻弹道具有不稳定性，如图11、图12所示，侵彻弹道呈现“J”字形弯曲弹道。与低速下大倾角着靶时侵彻弹道的偏转程度相比，高速下小倾角着靶时侵彻弹道的偏转程度更为严重，相对偏转率达到31.3%。

4)针对侵彻过程中侵彻深度发生逆减的临界速度给出了工程计算模型，从中可以得到临界速度与弹体的强度呈正比，与靶板的强度呈反比；结合实验数据验证了理论模型的可靠性。

[1] 高飞，张国凯，纪玉国，等.卵形弹体超高速侵彻砂浆靶的响应特性[J]. 兵工学报, 2020, 41(10): 1979-1987.

GAO F, ZHANG G K, JI Y G, et al. Response characteristics of hypervelocity ogive-nose projectile penetrating into mortar target[J]. Acta Armamentarii, 2020, 41(10): 1979-1987. (in Chinese)

[2] GOLD V M. Concrete penetration by eroding projectiles: experiments and analysis[J]. Journal of Engineering Mechanics, 1996, 122(2):145-152.

[3] 练兵.高速动能杆对混凝土靶的侵彻毁伤研究[D].北京：北京理工大学,2010.

LIAN B. Penetration and damage of concrete with high velocity kinetic energy rod[D]. Beijing: Beijing Institute of Technology,2010.(in Chinese)

[4] 练兵,蒋建伟,门建兵,等.高速长杆弹对混凝土靶侵彻规律的仿真分析[J].高压物理学报, 2010, 24(5): 377-382.

LIAN B, JIANG J W, MEN J B, et al. Simulation analysis on law of penetration of long-rod projectiles with high speed into concrete[J].Chinese Journal of High Pressure Physics, 2010, 24(5): 377-382.(in Chinese)

[5] 宋梅利,李文彬,王晓鸣,等.弹体高速侵彻效率的实验和量纲分析[J].爆炸与冲击, 2016, 36(6): 752-758.

SONG M L, LI W B, WANG X M, et al．Experiments and dimensional analysis of high-speed projectile penetration efficiency[J].Explosion and Shock Waves, 2016, 36(6): 752-758. (in Chinese)

[6] DAVIS R N, NEELY A M, JONES S E. Mass loss and blunting during high-speed penetration[J]. Archive Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science, 2004, 218(9):1053-1062.

[7] LIU C, ZHANG X,CHEN H, et al. Experimental and theoretical study on steel long-rod projectile penetration into concrete targets with elevated impact velocities[J]. International Journal of Impact Engineering,2019, 138:103482.

[8] KONG X Z, WU H, FANG Q, et al. Projectile penetration into mortar targets with a broad range of striking velocities: test and analyses[J]. International Journal of Impact Engineering, 2017, 106:18-29.

[9] KONG X Z, WU H, FANG Q, et al. Rigid and eroding projectile penetration into concrete targets based on an extended dynamic cavity expansion model[J].International Journal of Impact Engineering, 2017, 100:13-22.

[10] CHEN X W, LI Q M. Transition from nondeformable projectile penetration to semi-hydrodynamic penetration[J]. Journal of Engineering Mechanics, 2004, 130(1): 123-127.

[11] ROSENBERG Z, DEKEL E. A critical examination of the modified Bernoulli equation using two-dimensional simulations of long rod penetrators[J]. International Journal of Impact Engineering, 1994, 15(5):711-720.

[12] WANG P, JONES S E. An elementary theory of one-dimensional rod penetration using a new estimate forpressure[J]. International Journal of Impact Engineering, 1995, 18(3): 265-279.

[13] 刘闯,张先锋,黄长强,等.半球头长杆弹高速侵彻半无限厚靶临界速度理论模型[J]. 振动与冲击, 2019, 38(9): 8-14.

LIU C, ZHANG X F, HUANG C Q, et al. Critical speed theoretical model for hemispherical long rod projectiles’ penetrating semi-infinite thick target at high velocity[J]. Journal of Vibration and Shock, 2019, 38(9): 8-14. (in Chinese)

[14] 王可慧,宁建国,李志康,等.高速弹体非正侵彻混凝土靶的弹道偏转实验研究[J].高压物理学报,2013, 27(4): 561-566.

WANG K H, NING J G, LI Z K, et al. Ballistic trajectory of high-velocity projectile obliquely penetrating concrete target[J].Chinese Journal of High Pressure Physics, 2013, 27(4): 561-566.(in Chinese)

[15] 钱秉文,周刚,李进，等.钨合金柱形弹超高速撞击水泥砂浆靶的侵彻深度研究[J].爆炸与冲击, 2019, 39(8): 083301.

QIAN B W, ZHOU G, LI J, et al. Penetration depth of hypervelocity tungsten alloy projectile penetrating concrete target[J].Explosion and Shock Waves, 2019, 39(8):083301. (in Chinese)

[16] 陈海华，张先锋，刘闯,等.基于弯管- 流线模型的长杆弹侵彻头部材料流动过程分析[J].兵工学报, 2019, 40(9): 1787-1796.

CHEN H H, ZHANG X F, LIU C, et al. Analysis of material flow around projectile nose by elbow-streamline model during long-rod projectile penetrating into steel target[J]. Acta Armamentarii, 2019, 40(9): 1787-1796.(in Chinese)

[17] 宋春明，李干，王明洋，等.不同速度段弹体侵彻岩石靶体的理论分析[J]．爆炸与冲击，2018，38(2): 250-257．

SONG C M，LI G，WANG M Y，et al．Theoretical analysis of projectiles penetrating into rock targets at different velocities[J].Explosion and Shock Waves，2018，38(2): 250-257. (in Chinese)

[18] 中国建筑科学研究院.混凝土强度检验评定标准[M]. 北京：中国计划出版社, 1988.

China Academy of Building Science. Standard for concrete strength inspection and evaluation [M]. Beijing: China Plans Publishing House, 1988. (in Chinese)

[19] TATE A. A theory for the deceleration of long rods after impact[J]. Journal of the Mechanics & Physics of Solids, 1967, 15(6):387-399.

[20] ALEKSEEVSKII V P. Penetration of a rod into a target at high velocity[J]. Combustion Explosion & Shock Waves, 1966, 2(2):63-66.

[21] TATE A. Long rod penetration models-Part II. Extensions to the hydrodynamic theory of penetration[J]. International Journal of Mechanical Sciences, 1986,28(9): 599-612.

[22] 徐晨阳.弹体高速侵彻典型岩石粑体作用过程研究[D].南京：南京理工大学,2018.

XU C Y. Research on the process of projectile penetrating into typical rock at high speed[D]. Nanjing: Nanjing University of Science and Technology,2018. (in Chinese)