面向战备完好的飞机群组预防性维护优化和备件预测方法

李婷， 刘林， 彭云程， 崔超雄， 薛非

(西安飞机工业(集团)有限责任公司， 陕西 西安 710089)

0 引言

为适应新时期飞机高强度服役和快速作战响应的发展趋势，部队实战化飞行训练任务加大，飞机维护模式和备件需求不确定性逐渐增加。而信息化和智能化的作战需求，也对以战备完好性为代表的各项健康性能指标提出的更高的要求。现有以工程经验为主导的事后/定期维护机制，和该既定机制下的备件管理方法，缺乏对飞机服役模式和运行状态的有效兼容，以及对备件需求规律的准确把握，很难满足装备发展“科学精准快速保障”的需求。

目前国内外针对以飞机为代表的航空设备预防性维护和备件优化，在定性和定量层面开展了一些基础性研究工作。定性研究方面，苏亨锔介绍了基于测试数据的航空装备视情维修研究整体思路。郑志霖介绍了民用飞机维修方案优化的工作项目流程，强调利用可靠性数据的重要性。定量研究方面，根据航空产品性质和用途的不同，可用度和运维成本是维护和备件优化的两个核心优化目标。Liu针对机身蒙皮采用三阶段维纳过程模型描述裂纹扩展，对每阶段设计不同的检测周期并优化预防性维修阈值。王华探讨了飞机维修控制在民用航空成本控制中的应用情况。杨力研究了复杂串并联航空系统寿命周期成本的优化算法。而在军用航空方面，战备完好性，或者可用度是更加常见的维修保障目标。马小兵研究了可用度约束下的航空产品寿命建模和优化。涂继亮等将可用度和保障率作为优化参数，对飞机的备件方案进行优化。陈博等基于DEVS-OODA模型对作战飞机备件需求进行了定量预测。陈云翔等基于分层赋时着色Petri网构建飞机编队仿真模型，优化保障资源配置。李岩等则考虑战时情况下的维护保障人员数量确定问题。然而，目前的研究在实际应用中仍存在一些不够完善的地方：1)维护方案以事后维护和简单的年龄维护为主，缺乏针对不同典型失效部件(寿命件、缺陷件、退化件等)构成系统的整体维护规划调度；2)备件预测技术往往和整机级维护方案脱节，导致不能较好反应飞机当前的维修水平和计划，导致备件过度或者不足的风险增大。

针对以上的问题，本文以提升飞机装备保障战备完好性(服役可用性)为目标，整体研究了飞机群组预防性维护调度计划建模和优化方法，以及基于既定最优维护计划的备件需求预测方法。具体地，分别针对典型寿命件和包含缺陷(潜在故障)态的部件，制定相应的个体维护方案，以此为基准安排飞机系统的整体预防性群组维护计划。通过结合马尔科夫过程(描述健康状态转移)和延迟时间模型(描述缺陷发展特点)，基于更新过程对基准检修窗口长度和各部件所需窗口数量开展联合解析优化，实现飞机系统平均可用度最大化。最后基于既定的系统层级最优维护计划，通过离散仿真算法对规划周期内的备件需求数量开展预测。对比现有的飞机维护和备件优化方面的研究，本文提出的方法有如下三方面的贡献：

1) 基于日历时间的群组维护框架，通过同时设置维护窗口单元，实现了对飞机典型失效件维护计划的协同规划，有效避免了维护资源浪费和停机时间过长的问题；

2) 通过高效的解析优化算法，实现了对飞机装备整机级可用度的快速精确计算，显著降低了维护规划的复杂度；

3) 群组维护策略驱动的备件预测技术，相比传统的纯数据驱动方法，能够更加紧密贴合飞机故障特点和维护方案，反映备件需求的物理统计分布特征。

剩余章节的结构安排如下。第一章介绍飞机装备维护保障相关问题，包括关键组件的故障特点，整体维护策略等。第二章开展面向战备完好的飞机检修模型构建和优化工作。第三章基于既定维护优化结果开展飞机备件需求预测的工作。第四章通过数值案例验证本论文模型方法对提升战备完好性的有效性。

1 问题描述

1.1 故障特点

考虑飞机装备的预防性检修计划，共覆盖个关键部件分系统。根据历史故障数据和运行维护记录，个检修部件分系统按照失效特点可以分为以下两类典型结构：1)寿命件；2)缺陷件。

1) 寿命件。寿命件只包含正常态和失效态两种状态，其失效时间服从一定的随机概率分布。典型的寿命件包括非金属产品，如橡胶密封圈等。寿命件一般可按定期更换处理。所有寿命件集合记为N。

2) 缺陷件。缺陷件的失效过程包括正常态、缺陷态和失效态三种状态。和寿命件相比，缺陷件在失效前会出现可识别的缺陷(进入缺陷态)。例如，轴承在使用过程中疲劳裂纹逐渐形成和扩展，扩展到一定程度则导致轴承振动信号出现显著变化。一般地，产品从缺陷状态到完全失效的时间较短，影响运行安全，因此需要制定检修计划尽早发现，一旦发现缺陷则安排维修更换工作。所有缺陷件集合记为N。

1.2 预防性维护和备件策略

根据两类部件的特点，寿命件进行定期更换，缺陷件进行定期检修。对于缺陷件，一旦检测发现缺陷，则立即更换。如果部件在检测周期内发生失效，则立即更换。相比于年龄维护策略，周期检修策略产生的维护计划确定性强，利于实际执行。为简单起见，本文假设所有部件失效均可立即发现(例如飞行过程中的传感器指示、飞机日常维护和测试)，并进行修复/更换处理。

所有部件在定期维护时进行的更换称为预防性更换(PR)，在失效时发生的更换称为修复性更换(CR)。一般而言，PR是按照既定维护计划进行的维护活动，确定性强，维护人员和设备可提前就位，因此飞机停机时间较短；CR取决于部件随机的失效时间，修复时一方面需要等待维护人员和设备就位，另一方面需要复杂的测试以定位故障部件，因此飞机停机时间较长。

部件维护时间可进一步分为两部分：1)维护固定时间，例如飞机从停机坪到机库的时间、维护前准备时间和维护后测试时间等；2)各部件专门进行维护的时间，为各部件属性。其中，维护固定时间是系统属性，可被所有部件维护时共享，因此考虑将多个部件的维护活动组合到一起，将各部件的更换检修周期设置为某一基础周期的整数倍，以共享从而减少飞机停机时间。该类维护策略也称为成组维护(block maintenance)。

综上分析，问题设定和飞机维护检修策略具体为：

1)寿命件进行定期更换；缺陷件进行定期检测，如果检测发现缺陷则进行预防性更换；如果某部件在维护周期内发生故障则立即进行故障更换。各部件失效相互独立；

2)所有部件的更换检测周期均为其中最短周期的整数倍，该最短周期也称为基础周期，记为；

4)当同一时刻多个部件进行维护时，系统维护时间为其中的最大值。任一部件进行维护均导致系统停机。

图1给出了系统维护策略示意图。四个部件各自的PR周期或定检周期为某一基础周期的整数倍。故障发生则系统停机立即进行修复(如寿命件2)。缺陷件检测时发现缺陷则立即更换(如缺陷件1在2时刻)，否则只进行检测(如缺陷件2)。

2 面向战备完好的维护优化

本节采用两阶段法建立飞机系统维护模型：1)部件级检修模型：分别根据寿命件和缺陷件的维护策略建立相应的可用度模型，通过最大化可用度确定部件级最优更换检测周期；2)在部件级模型的基础上建立系统战备完好(可用度)模型，然后以部件级优化结果为基础确定系统级最优维护周期，最后以最大化系统可用度为目标优化系统维护策略。两阶段法的优点是可以解除系统状态耦合，简单合理，可以处理规模较大的多部件系统。

图1 飞机成组维护策略与停机时间示意图Fig.1 Diagram of aircraft group maintenance strategy and downtime

2.1 部件级维护建模

211 寿命件

假设某寿命件∈N的失效时间(连续工作时间)分布函数(CDF)为()，若飞机在服役期间的使用率为，则等效于部件∈N的失效时间(日历时间)分布为()。为简单起见，省略使用率参数，统一使用()代表折合后的失效时间分布，密度函数(PDF)为()。

(1)

式中：()表示部件在时间内的失效次数。若忽略一个周期内失效次数超过2次的可能(避免预防性更换丧失意义)，则

(2)

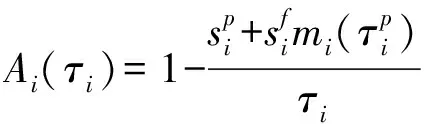
(3)

212 缺陷件

由于缺陷件进行周期检，检修后的部件一定处于正常态，以周期检时间点为观测点、以处于正常态的年龄为状态，缺陷件的状态演化可用马尔可夫过程建模。为求解稳态平均可用度，需要求解该缺陷件的稳态状态概率。

记该缺陷件的定检周期为，令=-，=-，=-。记检修后部件年龄为0(缺陷更换)的概率为，年龄为的概率密度函数为()，>0。考虑到实际中一个定检周期内部件失效次数不会太多，因此只考虑一个周期内最多发生一次失效，建立稳态方程。共分为1～4四种情形。

1)1：初始年龄为0(更换后)，周期结束时需要进行PR，转移概率为(0|0)

如果部件在周期内发生失效(一次)，则该情况的转移概率为

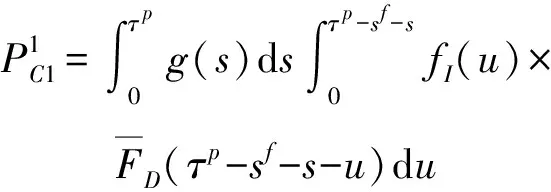
(4)

如果部件在周期内未发生失效，则该情况的转移概率为

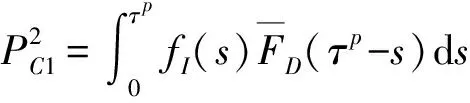
(5)

综上，1情况的转移概率为

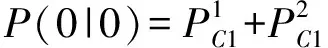
(6)

2)2：初始年龄为，周期结束时需要进行PR，转移概率为(0|)

当初始年龄为时，部件剩余寿命的概率密度为

(7)

因此，如果部件在周期内发生失效，则该情况的转移概率为

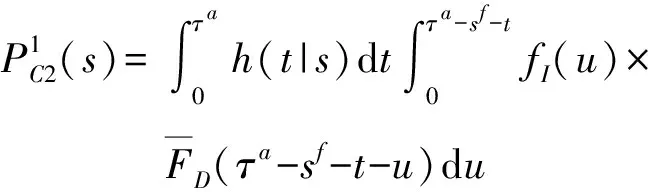
(8)

如果部件在周期内未发生失效，则该情况的转移概率为

(9)

综上，2情况的转移概率为

(10)

3)3：初始年龄为0(更换后)，周期结束时无需进行PR，转移概率密度(|0)

如果周期内部件发生失效(一次)，则失效时间为--，且故障更换后的部件在剩余周期内一直处于正常态；另一方面，如果未发生失效，则必然要求该部件一直处于正常态，且=。综上，3情况的转移概率密度函数为

(11)

式中：(·)表示示性函数：如果括号内条件成立则函数值为1；否则为0。(≤-)表示只有≤-时才可能存在失效情况。

4)4：初始年龄为，周期结束时无需进行PR，转移概率密度(|)

如果周期内部件发生失效(一次)，则失效时间为--，且故障更换后的部件在剩余周期内一直处于正常态；另一方面，如果未发生失效，则必然要求该部件一直处于正常态，且=+。综上，4情况的转移概率密度函数为

(12)

式中：()为Dirac函数。第二项使用(--)表示只有当=+时才成立。(·|)由(7)式确定。

综合1～4，可确立稳态状态概率方程求解检修后年龄为0的概率和年龄为的概率密度函数()，>0，如(13)式所示：

(13)

(14)

易知方程组(14)式为(+1)维线性方程组，较易求解。值得注意的是，也表示部件在检测点进行PR的概率，1-则表示在周期检测点只进行检测活动的概率。

为求解部件的平均可用度，需要计算它在检测周期内发生失效的概率。如果初始年龄为0，则失效概率为

(15)

如果初始年龄为，则失效概率为

(16)

则缺陷件的平均可用度为

(17)

2.2 系统群组维护优化

飞机系统级维护采用成组维护策略，即各部件的更换检测周期为其中最短周期(称为基础周期)的整数倍，以共享维修固定时间，减少飞机停机时间。系统级成组维护优化在部件级维护策略基础上进行。

根据(3)式或(17)式，部件∈N∪N的部件级最优更换检测周期为

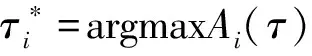
(18)

ki=τ∗iτ∗c∗,Ai(⌊τ∗i/τ∗c∗」τ∗c∗)> Ai(⌊τ∗i/τ∗c∗」τ∗c∗+τ∗c∗)τ∗iτ∗c∗+1,其他ìîíïïïïïïïï

(19)

式中：⎣·」表示向下取整。显然=1。

在根据(19)式确定各部件周期倍数{,∈N∪N}之后，通过调整基础周期以确定各部件的调整后维护周期。因此，基础周期为飞机系统级维护的优化决策变量。

下面计算成组维护下飞机系统的平均可用度。首先注意到所有部件维护周期的最小公倍数即为系统的更新周期，记为×。

当=,=1,2,…,时(称为第个系统维护点)，计划进行维护(包括检测和预更换)的部件集合为C，即

C={|可被整除}

(20)

(21)

(22)

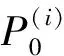
(23)

根据(23)式和变换定义，维护时刻飞机系统平均计划维护停机时间为

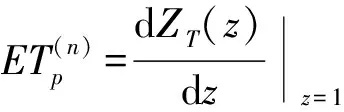
(24)

(25)

综上，综合(24)式、(25)式飞机系统在成组维护策略下的平均可用度为

(26)

最优基础周期可通过最大化系统平均可用度确定，即

=argmax()

(27)

根据(19)式，部件在系统级成组维护策略下的更换检测的周期为。

3 飞机备件预测仿真

本节在飞机成组维护策略基础上确定各部件在规划周期内的备件需求量。各部件在进行PR和CR时均产生备件需求，理论上计算规划周期内备件需求量的概率分布较为复杂，因此本节给出备件需求量的仿真算法。

设规划周期为，其中为成组维护策略中的基础周期。定义|N|×1向量defect表示各缺陷件缺陷发生时间；(|N|+|N|)×1维向量fail和spare分别表示各部件失效发生时间和总备件需求量。备件需求量的仿真流程如图2所示。仿真算法的核心思路是：

1)以每一个基础维护周期开始时刻为观测点，根据各部件仿真失效时间确定在观测点前一个周期内是否进行CR(更新defect和fail预计值)，直至所有部件的预计(仿真)失效时间均在当前观测点之后；

2)根据成组策略确定当前观测点需要进行预防性维护的部件集合C。其中所有寿命件和已出现缺陷的缺陷件均需要PR。对PR件更新defect和fail预计值；

3)每次PR和CR对应部件的备件需求数加1，过程直至观测点到达为止。

图2算法可得到一次仿真样本，重复10次可统计确定各部件所需备件量的统计分布和平均值等。所得备件需求预测结果可根据实际情况制定和优化备件订购策略，此部分内容不作为本文讨论重点。

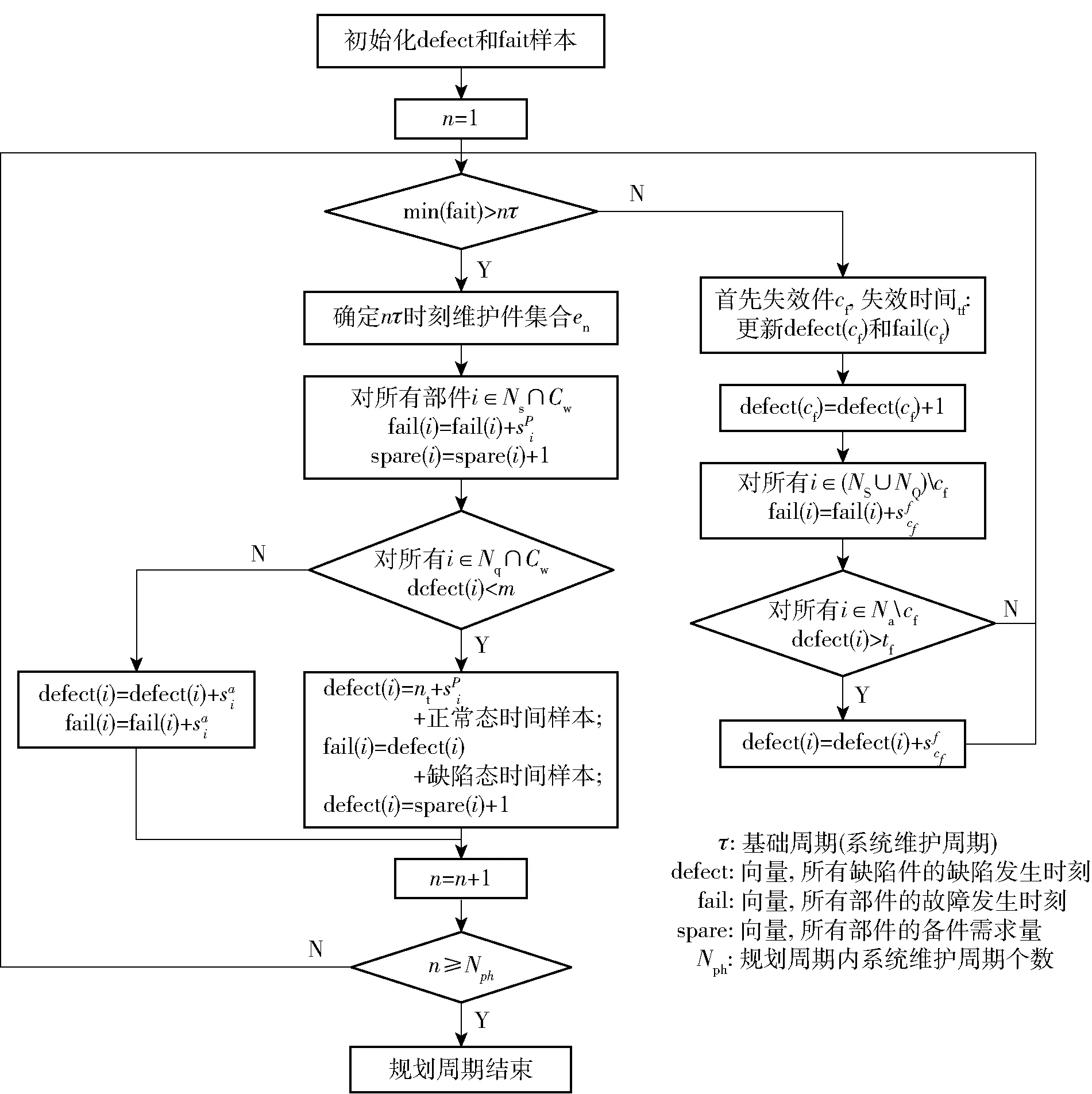
图2 飞机系统规划周期内各部件备件需求量仿真流程Fig.2 Simulation flow chart of spare parts demand in the planning horizon of the aircraft system

4 算例

根据第2节和第3节中的飞机维护和备件预测模型，本节给出相应数值算例，并说明所提出的成组维护策略在提高使用可用度方面的效果。

假设飞机检修计划共涵盖10个设备(部件)，其中5个部件属于寿命件(定期更换)，5个属于缺陷件(定期检测)。由于飞机设备多为机电类设备，因此不失一般性考虑威布尔分布用来描述部件的失效时间。威布尔分布的CDF和PDF分别为

(28)

式中：为尺度参数，反映特征寿命大小；为形状参数，反映失效机理。特别地，取值大于1，表示失效率递增，反映机电类产品疲劳、磨损、腐蚀等失效机理。

对所有10个部件进行编号，假设1号～5号表示缺陷件，6号～10号表示寿命件，对应的寿命参数如表1所示。

表1 飞机缺陷件和寿命件寿命参数

假设飞机每次进行维护时所需固定时间=12 h，包括等待、入库，初步拆卸、人员与设备准备时间、维护结束后测试等，此类时间为系统层时间，不计入部件层维护活动。各部件检测时间、预防性更换时间，故障更换时间如表2所示。

表2 飞机各部件检测和更换时间

表3 飞机各部件的部件级维护优化参数

(29)

两种系统可用度计算结果如图3所示。最优基础周期为=288 h(12 d)，对应可用度最大(=0900 5)。可以看出，采用成组维护策略后系统可用度提高效果明显，原因是成组维护可将多个部件维护进行组合，实现多任务并行和共享系统层维护固定时间。

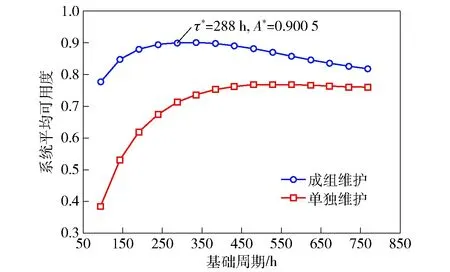
图3 两种维护策略下的系统可用度对比Fig.3 Comparison of system availability under the two maintenance strategies

表4给出在最优基础周期下各部件在系统层级的维护周期(检测或预防性更换)，并给出了各缺陷件在一个检测周期内失效不超过1次的概率，以及各寿命件在一个预防性更换周期内失效不超过2次的概率。从表4中可以看出，这些概率值均非常小，验证了21节为简化建模所作假设是合理的。

表4 各部件维护周期内失效超过1次的概率

进一步，可以考察系统维护准备时间对系统可用度的影响。

图4给出了成组维护和单独维护策略下可用度随变化曲线图。

显然可用度随增大而减小，此外图4还表明随着增大，两种策略间的差距略有增大，表明成组维护效果提升明显。此外，一个特别的现象是当减小接近0时，两种策略效果仍有较大差距，这是因为成组维护除了能共享，更重要的是还能够使得多预防性维护任务并行进行，较少停机时间。

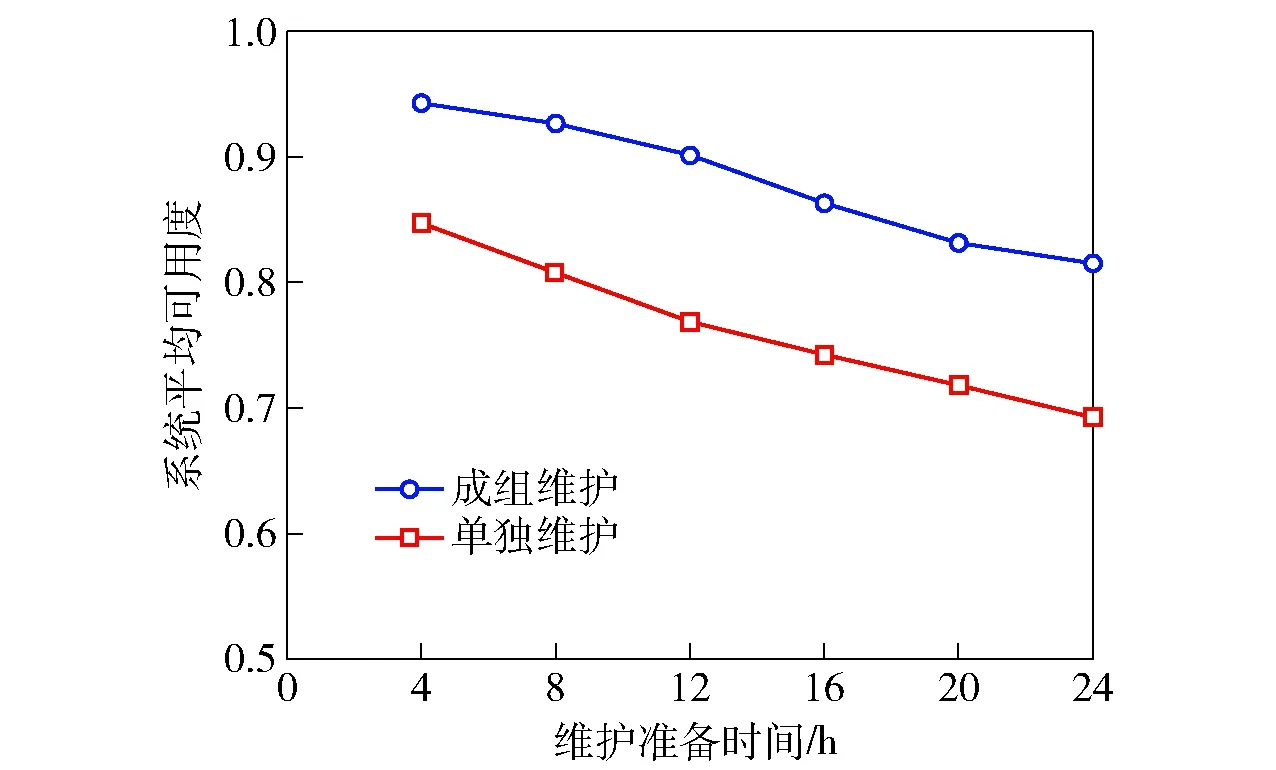
图4 系统可用度随维修固定时间ts变化图Fig.4 Variation of system availability with fixed maintenance time of ts

最后在给定维护策略下，假定规划周期为1年，根据图2仿真流程(仿真1 000次)计算各部件在规划期内的备件需求预测分布，结果如图5所示；平均备件需求量如表5所示。

表5 规划期(1年)内平均备件需求量

图5 各部件在规划周期(1年)内的备件需求量分布Fig.5 Spare parts demand distribution within the planning period (1 year) of each component

5 结论

本文以优化飞机可用度为目标，针对寿命件和缺陷件制定成组维护策略、建立部件可用度和系统可用度模型，最后在优化策略的基础上实现备件需求预测。该维护策略可组合多部件维护活动，具有优势：1)多维护任务并行进行；2)共享系统层维护固定时间，从而达到减少飞机维护停机时间、提高使用可用度的目的。优化过程分为两阶段：首先建立各部件可用度模型，进行部件级策略优化；在此基础上，确定各部件维护周期倍数，建立系统可用度模型，最终优化系统级策略。本文提供的数值算例表明成组维护策略相比于各部件独立维护对飞机系统可用度提升明显，备件需求分布仿真预测可对后续备件订购优化提供基础。

[1] 涂继亮, 余洪, 余松, 等. 基于性能保障分析的飞机备件需求预测模型 [J]. 海军航空工程学院学报, 2019, 34(4): 356-362.

TU J L, YU H, YU S, et al. Aircraft spare parts requirement forecasting model based on performance support analysis[J]. Journal of Naval Aeronautical and Astronautical University, 2019, 34(4): 356-362. (in Chinese)

[2] 王华. 飞机维修控制在成本控制中的应用 [J]. 科技创新与应用, 2017(16): 297.

WANG H. The application of aircraft maintenance in costs control[J]. Technology Innovation and Application, 2017(16): 297. (in Chinese)

[3] 苏亨锔. 测试数据下的航空装备视情维修研究 [J]. 设备维修与管理, 2018(11): 54-55.

SU X J. Condition-based maintenance of aerial equipment given testing data[J]. Plant Maintenance Engineering, 2018(11): 54-55. (in Chinese)

[4] 郑志霖, 叶晓东. 基于统计分析方法的飞机维修方案优化 [J]. 航空维修与工程, 2020(11): 29-33.

ZHENG Z L, YE X D. Optimization of aircraft maintenance scheme based on statistical analysis method[J]. Aviation Maintenance & Engineering, 2020(11): 29-33. (in Chinese)

[5] LIU J Q. Maintenance model of aircraft structure based on three-stage degradation process [J]. Computers & Industrial Engineering, 2021, 157: 107335.

[6] 杨力, 马小兵. 维修- 更换串联系统贮存可用度建模及费用分析 [J]. 兵工学报, 2015, 36(3): 552-558.

YANG L, MA X B. Storage availability modeling and cost analysis for a repair-replacement series system[J]. Acta Armamentarii, 2015,36(3):552-558. (in Chinese)

[7] 祝华远, 李军亮, 孙鲁青. 武器装备通用质量特性管理综述 [J]. 兵工自动化, 2021, 40(2): 13-17.

ZHU H Y, LI J L, SUN L Q. Overview of weapon equipment general quality characteristics management[J]. Ordnance Industry Automation, 2021, 40(2): 13-17. (in Chinese)

[8] 马小兵, 杨力. 贮存可用度约束下的可修系统寿命评估与优化 [J]. 系统工程与电子技术, 2015, 37(3): 572-576.

MA X B, YANG L. Life evaluation and optimization for a repairable system under the constraints of storage availability[J]. System Engineering and Electronics, 2015, 37(3): 572-576. (in Chinese)

[9] 陈博, 徐常凯, 徐启丰. 基于DEVS-OODA 模型的作战飞机备件保障仿真研究 [J]. 物流科技, 2018, 41(11): 129-131.

CHEN B, XU C K, XU Q F. Simulation of spare parts emergency support for carrier-based aircraft based on DEVS-OODA[J]. Logistics Sci-Tech, 2018, 41(11):129-131. (in Chinese)

[10] 陈云翔, 李岩, 蔡忠义, 等. 基于HTCPN的飞机维修保障资源配置方法 [J]. 系统工程与电子技术, 2020, 42(9): 2130-2139.

CHEN Y X, LI Y, CAI Z Y, et al. Allocation method of aircraft maintenance support resources based on HTCPN[J]. Systems Engineering and Electronics, 2020, 42(9): 2130-2139. (in Chinese)

[11] 李岩, 陈云翔, 蔡忠义,等. 战时军用飞机维修保障人员数量确定方法 [J/OL]. 火力与指挥控制.http://kns.cnki.net/kcms/detail/14.1138.TJ.20200925.1042.020.html.

LI Y, CHEN Y X, CAI Z Y, et al. Method for determining the quantity of maintenance support personnel of military aircraft in wartime[J/OL]. Fire Control & Command Control, http://kns.cnki.net/kcms/detail/14.1138.TJ.20200925.1042.020.html. (in Chinese)

[12] DE JONGE B, JAKOBSONS E. Optimizing block-based maintenance under random machine usage [J]. European Journal of Operational Research, 2018, 265(2): 703-709.

[13] KE H, YAO K. Block replacement policy with uncertain lifetimes [J]. Reliability Engineering & System Safety, 2016, 148: 119-124.

[14] LAGGOUNE R, CHATEAUNEUF A, AISSANI D. Opportunistic policy for optimal preventive maintenance of a multi-component system in continuous operating units [J]. Computers & Chemical Engineering, 2009, 33(9): 1499-1510.

[15] BERRADE M D, SCARF P A, CAVALCANTE C A V. A study of postponed replacement in a delay time model [J]. Reliability Engineering & System Safety, 2017, 168: 70-79.

[16] VAN OOSTEROM C D, ELWANY A H, CELEBI D, et al. Optimal policies for a delay time model with postponed replacement [J]. European Journal of Operational Research, 2014, 232(1): 186-197.

[17] YANG L, MA X B, ZHAI Q Q, et al. A delay time model for a mission-based system subject to periodic and random inspection and postponed replacement [J]. Reliability Engineering & System Safety, 2016, 150: 96-104.

[18] HUANG W Y, CHENG J S, YANG Y. Rolling bearing fault diagnosis and performance degradation assessment under variable operation conditions based on nuisance attribute projection [J]. Mechanical Systems and Signal Processing, 2019, 114: 165-188.

[19] SHAFIEE M, FINKELSTEIN M. An optimal age-based group maintenance policy for multi-unit degrading systems [J]. Reliability Engineering & System Safety, 2015, 134: 230-238.

[20] KROES M J, WATKINS W A, DELP F. Aircraft maintenance & repair [M]. 7th ed. New York，NY，US: McGraw-Hill, 2013.

[21] ZHANG C X, LI Q, LIU Y K. Optimal replacement policy with minimal repair and preventive maintenance of an aircraft structure subjected to corrosion [J]. Soft Computing, 2020, 24(1): 375-384.

[22] REN H, CHEN X, CHEN Y. Reliability based aircraft maintenance optimization and applications [M]. London，UK: Academic Press, 2017.

[23] LIU B, YEH R H, XIE M, et al. Maintenance scheduling for multi-component systems with hidden failures [J]. Ieee Transactions on Reliability, 2017, 66(4): 1280-1292.

[24] QIU S Q, MING H X G. Reliability evaluation of multi-state series-parallel systems with common bus performance sharing considering transmission loss [J]. Reliability Engineering & System Safety, 2019, 189: 406-415.

[25] WU D, CHI Y Y, PENG R, et al. Reliability of capacitated systems with performance sharing mechanism [J]. Reliability Engineering & System Safety, 2019, 189: 335-344.