不同端盖厚度的圆柱形装药壳体破片初速分布

高月光， 冯顺山， 刘云辉， 黄岐

(北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081)

0 引言

破片型战斗部利用炸药爆炸后产生具有一定动能的破片来毁伤目标，破片初速是研究和评估战斗部威力和防护结构性能的重要指标。战斗部通常是圆柱形装药壳体，采用一端起爆的方式。许多研究人员通过试验、数值仿真和理论分析等方法对破片初速进行了研究，并获得了可以解释破片形成和预测破片初速的理论和计算公式，研究成果为武器设计、公共安全、反恐等领域提供必要的参考。

在计算圆柱形装药壳体破片初速的理论和公式中，格尼公式因其简单、精度高而广泛应用。基于一些简单的假设和能量守恒规律，格尼提出了计算破片初始速度的经典公式，其中破片初速与炸药和壳体质量比相关，公式如下：

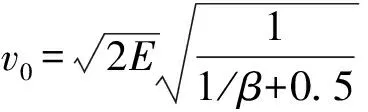
(1)

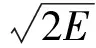
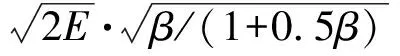
(2)

孔祥韶等对圆柱形装药壳体的动态过程进行了研究，发现轴向稀疏波会造成靠近端部破片初速的降低。郭志威等研究了轴向稀疏波对破片初速的影响，发现轴向稀疏波对破片加速过程有显著影响。此外，他们还进行了X光试验，研究了不同数量端盖的圆柱形装药壳体破片初速情况，结果表明端盖的存在能够减弱稀疏波对破片初速的影响。高月光等对两端带有空气段的圆柱形装药壳体进行了数值研究，发现轴向稀疏波与炸药同时作用于空气段壳体，使其破裂成具有一定速度的破片，并得到了两端带有空气段的圆柱形装药壳体破片初速的轴向分布规律。

在上述理论和计算模型中，可以发现轴向稀疏波通过影响破片加速过程来降低破片初速，而端盖的存在会削弱轴向稀疏波作用。然而，少有研究量化端盖对轴向稀疏波和破片初速的影响。而在实际应用中，战斗部大部分为两端带不同厚度端盖的圆柱形装药壳体，端盖的存在增加了破片的速度，提高了有效破片数，破片初速的合理预测对战斗部毁伤效能分析及结构设计具有十分重要的意义，可克服因只采用格尼速度计算破片初速造成对战斗毁伤性能的过高评估。因此，本文研究的两端有不同厚度端盖的圆柱形装药壳体破片初速分布具有更大的实际应用价值。本文在理论分析的基础上，采用数值仿真方法对一端中心起爆且带不同厚度端盖的圆柱形装药壳体进行研究，分析其加速过程，在格尼公式的基础上建立的破片初速分布公式，给出其适用范围，并通过试验和数值仿真进一步验证了所提出的公式的正确性。

1 理论分析

图1为两端带有不同厚度端盖的圆柱形装药壳体横截面示意图，装药为一端中心起爆，和为起爆端和非起爆端端盖厚度，和分别代表装药和壳体的直径，为壳体长度。在实际应用中，圆柱形装药壳体通常是薄壁壳体，且两端端盖的厚度也不会是无穷大的。因此端盖厚度可以通过壳体厚度进行表征。

建立起如图1所示的坐标系，坐标原点为起爆点，方向由起爆端指向非起爆端。在真实战斗部中，壳体通常为细长壳体，且轴向稀疏波对起爆端和非起爆端破片初速的影响距离分别为2和，为装药半径。因此，本文讨论中的圆柱形装药壳体均假设长度大于两倍装药直径来避免两端稀疏波的相互叠加影响。

图1 两端带不同厚度端盖的圆柱形装药壳体横截面图Fig.1 Cross-section of cylindrical charge shell with end caps at the two ends

下面推导端盖破片速度与圆柱壳体破片速度，依据动量守恒定理，得到端盖和壳体的动量守恒方程为

()d·d=d·d

(3)

式中：为圆柱壳体或端盖的密度；为圆柱壳体或端盖的厚度(端盖厚度记为)；为爆轰产物与金属壳体的接触面积，积分可得

(4)

则圆柱壳体和端盖的速度分别为

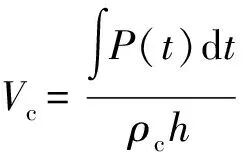
(5)

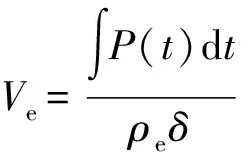
(6)

(7)

式中：下标e代表端盖；下标c代表圆柱壳体。由上述公式可得，圆柱壳体破片与端盖破片速度比是关于壳体密度与厚度乘积的比。因此，提出端盖厚度无量纲参数和为起爆端和非起爆端端盖厚度和密度乘积与壳体厚度和密度乘积的比值(=，=)，和为起爆端和非起爆端端盖密度。当两者材料相同时，其速度之比仅为端盖与壳体厚度的函数。

格尼公式是基于装药与壳体的动量守恒和能量守恒得到的，本质是关于装药与壳体质量比的函数。端盖本质上也是属于壳体，其产生的破片也占用了炸药部分能量，因此在求解端盖厚度对圆柱壳体破片速度的影响时，采用无量纲参数和可以很好地表征端盖部分壳体质量对于圆柱壳体破片速度影响。端盖厚度的增加，本质相当于增加了不同轴向位置处的质量比，进而改变了破片速度，能够反应无量纲中因变量与自变量的因果关系，反映现象的本质。轴向位置通过与装药直径相比得到无量纲参数本质也是反映轴向位置处质量比的变化，进而改变轴向位置处的破片速度。因此，得到新的不同端盖厚度圆柱形装药壳体破片速度轴向分布公式为

(8)

2 数值模拟

2.1 仿真方法

光滑粒子流体动力学(SPH)方法是求解强动载条件下材料动力学响应的一种先进仿真方法，其能够有效避免材料大变形时网格畸变问题，这是拉格朗日方法所不能解决的。Randles等采用SPH方法，通过光滑粒子和广义边界条件等改进方法，对圆柱形装药壳体的破碎进行了分析，仿真结果与实验结果吻合较好。SPH是一种无网格方法，广泛用于模拟材料瞬时动态大变形。SPH方法可以避免欧拉网格和材料边界问题。在过去的几年中，许多研究人员利用SPH方法对材料动态冲击进行了模拟，仿真结果均与实验结果吻合较好。

SPH方法是基于插值理论，利用插值函数将连续动力学转化为积分方程。对于函数()在参数定义的核函数的半径内的核估计〈()〉，可以通过对相邻粒子积分函数()得到：

(9)

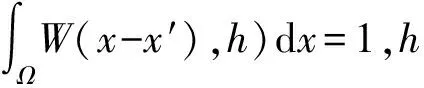
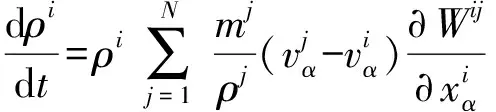
(10)

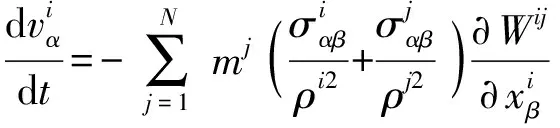
(11)

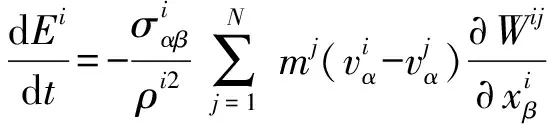
(12)

因为圆柱形装药壳体是对称的，所以只需要对它的四分之一进行建模。考虑到SPH方法为无网格方法，模型中的材料是由大量的粒子构成的。粒子是独立的，它们之间的关系由上述方程确定。实验证明，SPH方法的准确性与粒子的大小有关。粒子越小，模拟的准确性越高，但也意味着将耗费更多的时间。李伟等采用SPH方法对不同直径的粒子模型进行了仿真，结果表明，直径为0.4 mm的粒子即可获得足够精度的结果，且该直径粒子在多篇关于破片速度仿真的文章中均获得比较理想的结果。考虑到计算精度和时间的平衡，将模拟中的粒子直径设置为相同的直径(0.4 mm)。

2.2 材料模型

本文中的壳体和炸药材料分别为AISI 1045钢和B炸药，这是研究壳体爆炸和破片初速的最常用材料。AISI 1045钢爆炸后会发生膨胀破裂，其过程可以采用Johnson-cook (JC)模型来描述：

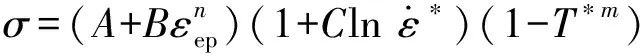
(13)

表1 1045钢JC参数[18]

炸药爆炸过程可以用JWL模型模拟：

(14)

式中：为炸药的爆压；为单位体积炸药内能；、、、和均为材料常数，炸药JWL参数如表2所示。

表2 B炸药JWL参数[19]

2.3 仿真模型验证

仿真模型只有具有足够的精度，才能用于模拟材料的真实性能。根据之前的分析，轴向稀疏波和端盖是影响破片初速的两个主要因素。因此，只要能验证这两个因素对破片初速的影响，就可以验证数值模型的精确性。轴向稀疏波对破片初速的影响可以采用黄广炎等的试验结果进行验证，端盖对破片初速的影响可以采用郭志威等的试验结果进行验证。黄广炎等的X光试验中的圆柱形装药壳体两端没有端盖，即端盖厚度为0。郭志威等的X光试验中两个圆柱形装药壳体中一个仅非起爆端带有端盖，另一个两端均带有端盖，端盖的厚度与壳体厚度相等。由于他们均采用X光设备获得的破片初速，因此试验结果具有很高的精度。三个试验的圆柱形装药壳体的参数如表3所示，其样本示意图如图2所示。依据他们的试验建立相应的数值仿真模型。

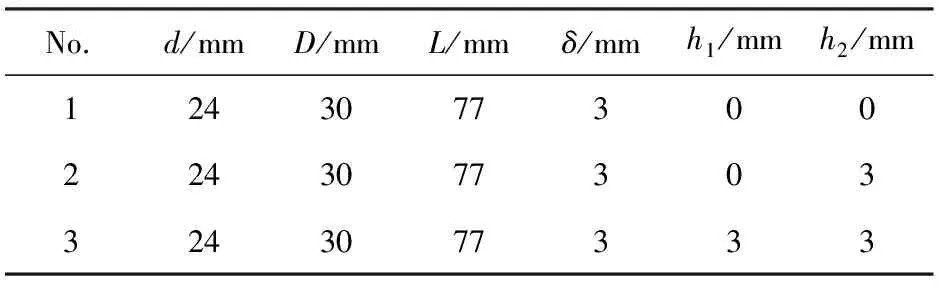
表3 黄广炎[9]和郭志威[11]试验中样本参数

数值仿真结果与试验结果对比如图3所示，其中为试验结果，为模拟结果。可以发现端部没有端盖的圆柱形装药壳体破片初速的仿真结果中，轴向稀疏波使得端部附近破片的速度明显减小，其破片初速的轴向分布与黄广炎等的试验结果具有很好的吻合性，结果表明仿真模型是能够精准模拟轴向稀疏波对破片初速的影响。同时与郭志威等的端部带有不同数量端盖的圆柱形装药壳体的试验结果对比表明，端盖的存在确实能够有效减弱轴向稀疏波对破片初速的削弱作用，从而提高端部破片初速，仿真得到的破片初速分布与试验获得的破片初速分布十分吻合，说明仿真模型是能够有效模拟端盖对于破片初速的影响，从而获得精确的破片初速分布。

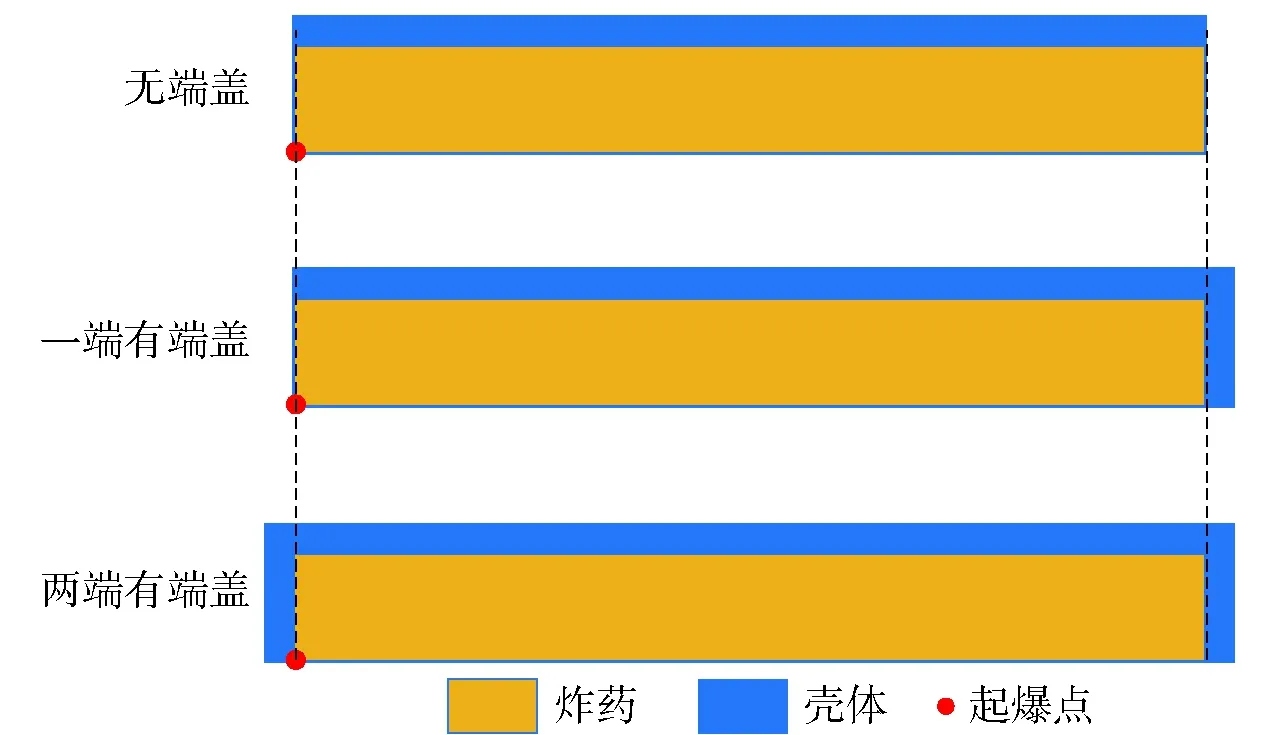
图2 试验样本示意图Fig.2 Schematic diagram of three experimental specimens

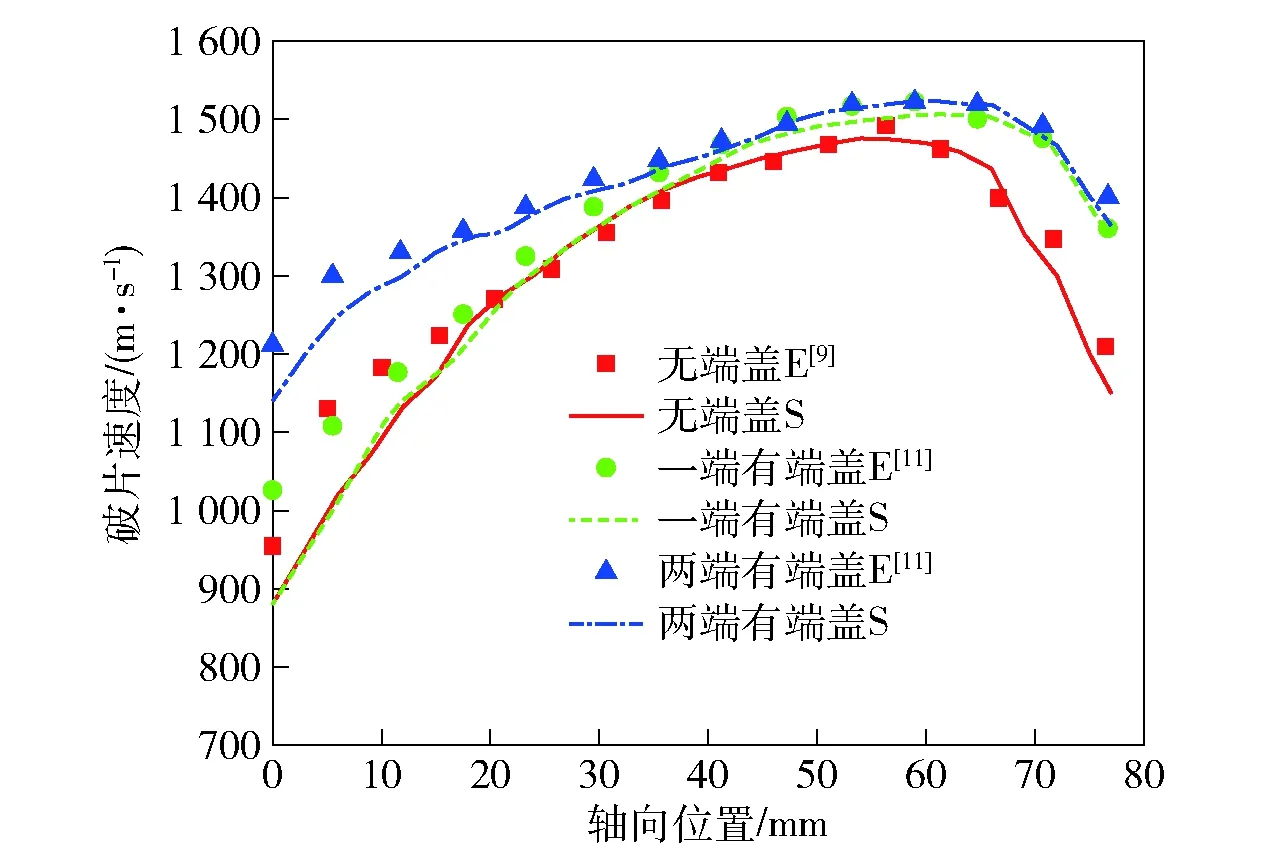
图3 试验结果与仿真结果比较图Fig.3 Comparison between numerical results and experimental data

综上所述，所建立的仿真模型是能够精确地模拟出端盖和稀疏波对破片初速的影响，因此可以用来进一步求解两端带有不同厚度端盖的圆柱形装药壳体破片初速的轴向分布。

2.4 仿真样本模型

通过前一节中对仿真模型的校核，结果表明其能够精确模拟端盖和轴向稀疏波对圆柱形装药壳体破片初速的影响，因此，利用该仿真模型，设置两端不同厚度的圆柱形装药壳体，求得两端不同厚度端盖的圆柱形装药壳体破片初速分布。建立的数值仿真模型如图4所示，两端带有不同厚度端盖的圆柱形装药壳体参数如表4所示。参数和为起爆端和非起爆端端盖厚度与壳体厚度的比值，其比值为0代表该端部没有端盖，仿真模型的粒子直径设置为相同的04 mm，每个仿真模型的粒子数见表4。

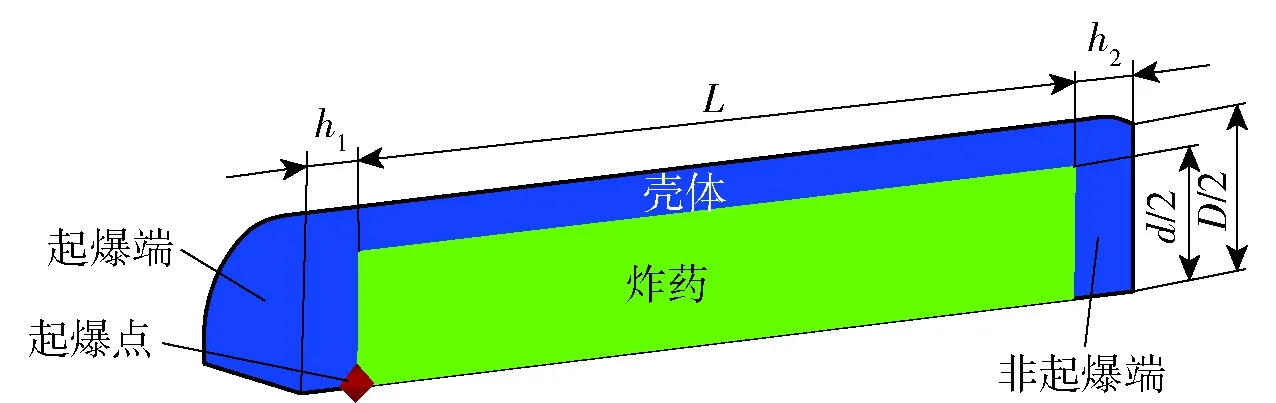
图4 两端带不同厚度端盖的圆柱形装药壳体仿真模型Fig.4 Numerical model for the cylindrical charge shell with different thick end caps

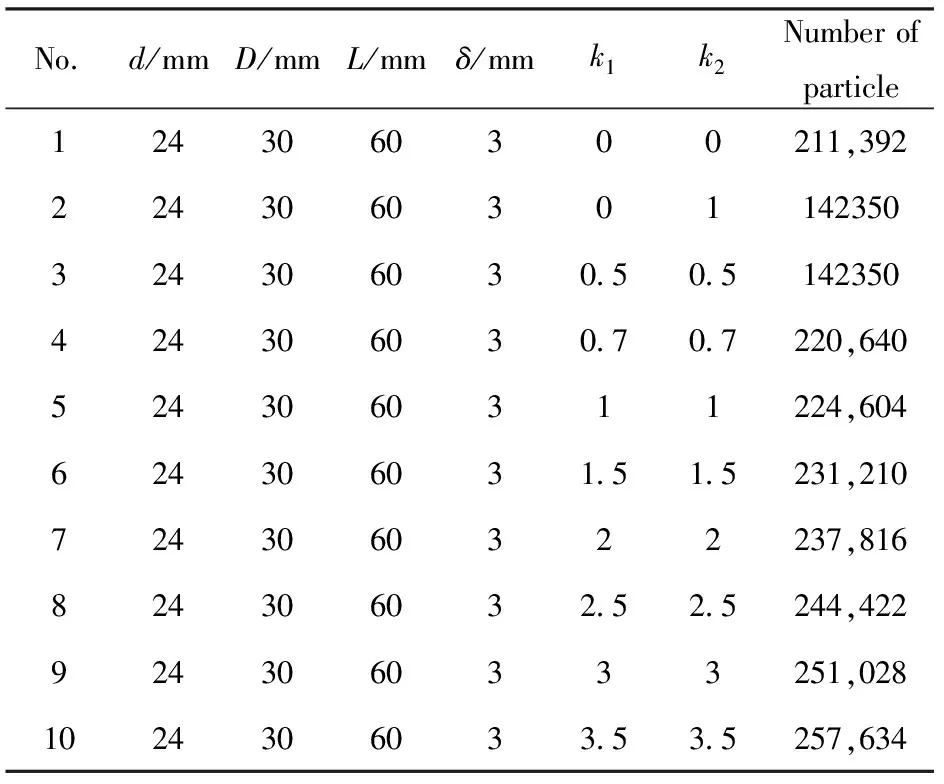
表4 10个带有不同厚度端盖的圆柱形装药壳体参数

3 结果与分析

由于壳体的长度足够长(>2)，两端的轴向稀疏波不会相互影响。因此，两端端盖厚度对破片初速的影响可以单独分析。

图5为起爆端破片的加速过程，表示起爆端端盖的厚度，=0表示起爆端无端盖。如图5所示,对于起爆端破片，只要存在端盖(无论厚度多少)，端盖会降低轴向稀疏波对初始冲击波的影响，使得破片在初始冲击波的加速作用下达到几乎相同的速度点，而没有端盖的壳体在初始冲击波的加速作用下由于轴向稀疏波的作用，速度只能达到点。随后的爆轰波继续加速起爆端壳体，使其速度从点达到点，可以发现，由于端盖的存在，壳体速度从点增加到了点，这是因为端盖减弱了轴向稀疏波对初始冲击波后爆轰波的削弱作用，但这种速度的增加并随端盖厚度而改变。此后，爆轰产物将破片初速从点增加到点。可以看出，起爆端端盖的存在显著提高了爆轰产物对破片的加速作用，且这种加速作用随着起爆端端盖厚度的增加而增强，破片初速从点增加到了点，其原因是起爆端端盖显著减少了爆轰产物的轴向分散和轴向稀疏波对爆轰产物的削弱作用。此外，起爆端端盖的存在也缩短了破片的加速过程，使破片能更快地达到最大速度，例如起爆端有端盖的圆柱形装药壳体产生的破片初速达到最大速度点的时间比无端盖的圆柱形装药壳体产生的破片初速达到最大速度点的时间提前早了15(25 μs)。

图5 靠近起爆端破片加速过程图Fig.5 Acceleration process of fragments from shell near the detonation end

图6所示为非起爆端破片的加速过程。同样的原因，由于非起爆端端盖的存在，壳体速度从点增加到点，但这种初始冲击波对壳体的加速效果并没有随着非起爆端端盖厚度的改变而改变。但不同于起爆端壳体加速过程的是，非起爆端端盖厚度的增加改变了后续爆轰波对壳体的加速作用，为此，破片初速能够从点提高到了点。对于非起爆端破片，非起爆端端盖的存在并没有增强爆轰产物对破片的加速作用，非起爆端带有端盖的破片初速从点增加到点的速度增加量与无端盖条件下破片初速从点增加到点的速度增加量接近，这是因为爆轰产物的运动方向是从起爆端指向非起爆端，这使得轴向稀疏波作用被后续爆轰产物所减弱，非起爆端爆轰产物对破片的加速作用受到轴向稀疏波的影响相对起爆端破片相对较弱，因此，后续爆轰产物加速作用受端盖厚度影响程度较小，不同厚度端盖对非起爆端破片的加速效应主要体现在爆轰波的加速作用显著增加。

从图5和图6中可以看出，起爆端端盖主要通过增加爆轰产物对破片的加速效应使得靠近起爆端破片初速相应增加，而非起爆端端盖主要通过增加爆轰波对破片的加速效应使得非起爆端破片初速相应增加。

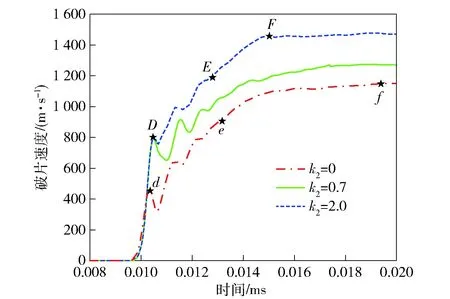
图6 靠近非起爆端破片加速过程图Fig.6 Acceleration process of fragments from the shell near the non-detonation end

两端带有不同厚度端盖的圆柱形装药壳体破片初速分布仿真结果如图7中散点所示，记为。其中爆轰产物不断地从起爆端向非起爆端运动，使得爆轰产物对非起爆端的破片的加速作用大于对起爆端的破片的加速作用，同时端盖又增加了爆轰波对非起爆端破片的加速效应；而对起爆端破片，端盖虽增加了爆轰产物的加速作用，但爆轰波加速作用并未显著增加。因此，相对起爆端破片，非起爆端破片增速更加明显，也更加接近格尼速度。

图7 带有不同厚度端盖的圆柱形装药壳体速度分布图Fig.7 Fragment velocity distribution for cylindrical charge shell with different thick end caps

4 破片初速分布公式

4.1 修正函数

如第3节所述，两端端盖的存在改变了破片的加速度过程，导致两端破片初速以不同程度的增加。黄广炎等提出的公式能够精准地预测两端没有端盖的圆柱形装药壳体破片初速的轴向分布，本文中破片初速分布将在黄广炎等提出的公式基础上建立，包含无端盖情况(==0)，并将其按照本文修正函数形式进行修正，修正函数表示如下：

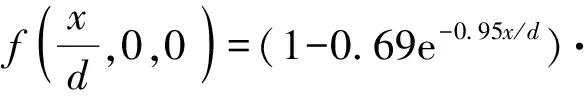
(15)

式中：表示离起爆点的轴向距离；表示装药直径；表示装药长度。由于新公式可以完全覆盖两端带有不同厚度端盖(包括厚度为0)的圆柱形装药壳体破片初速轴向分布，因此可以在(15)式的基础上建立起破片初速分布公式的修正函数，其表达式为

(16)

式中：、、和是常数，其值可以通过仿真结果拟合得到。不同端盖厚度条件下的这些常数是不同的，可以先求解其在不同端盖厚度条件下的值，再分析其与端盖厚度的关系。

由于圆柱形装药壳体满足两端的轴向稀疏波作用不会相互影响，基于黄广炎等的理论，从起爆端到最大破片初速位置之间的破片初速由起爆端端盖厚度决定，根据这部分破片初速分布可以计算出常数和系数。同样，从非起爆端到最大破片初速位置之间的破片初速由非起爆端端盖厚度决定，通过这部分破片初速分布可以得到常数和。

根据上述分析，在计算常数和时，假设(16)式右侧括号为1，即破片初速仅由起爆端的端盖厚度决定。常数可以由起爆端处破片初速得到，系数可以通过拟合这部分破片初速分布计算得到。常数和可以用类似的方法得到。由此得到不同端盖厚度条件下的系数如表5所示，系数与、的关系如图8所示，显然，在不同的端盖厚度条件下，系数发生了变化。

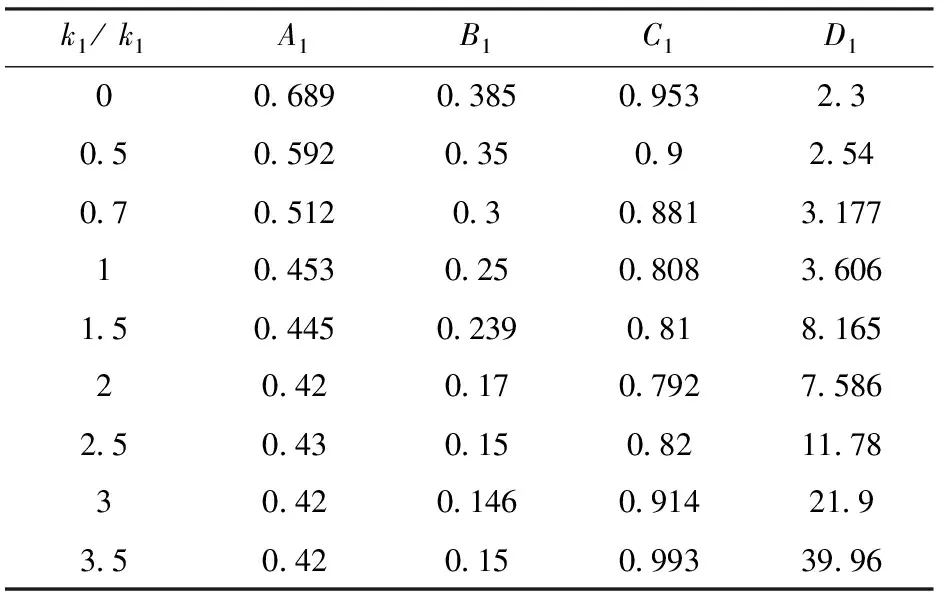
表5 9个仿真模型得到的修正函数参数

图8 参数与k1和k2的关系图Fig.8 Relationship between the parameters and the ratios k1 and k2

常数、、和与、之间存在明显的函数关系，由于两端破片初速不相互影响，常数和只与起爆端端盖厚度有关，即只与有关，与无关，常数和可以由来计算，常数和只与非起爆端端盖厚度有关，即只与有关，与无关，常数和可以由来计算。由图8中系数、、和与、之间的关系也可以得到，系数、与比值的关系分别为指数关系和二次函数关系，系数、与比值的关系可以用指数函数表示。其关系如下:

=+e-

(17)

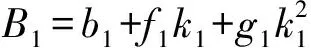
(18)

=+e-

(19)

=+e-

(20)

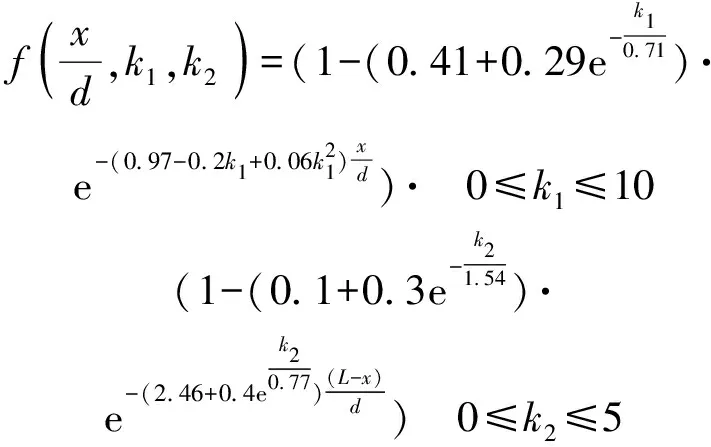
(21)

将(21)式代入(8)式，即可获得计算两端带不同厚度端盖的圆柱形装药壳体破片初速分布公式，由(8)式计算的计算结果与仿真结果的对比如图7中所示，其中散点代表仿真值，记为，曲线代表计算值,记为。可以发现不同厚度端盖条件下公式的计算结果与仿真结果均具有较好的吻合性，相对误差最大不超过46，因此，提出的破片初速公式可以用来计算两端带有不同厚度端盖的圆柱形装药壳体的破片初速轴向分布，并且包括常见两端没有端盖的情况(端盖厚度为0)，具有更广泛的适应性。

4.2 公式验证

为了验证提出的破片初速公式的准确性，采用前人的试验结果进行验证。试验中的壳体和炸药材料为1045钢和B炸药。试验中壳体具有三种不同厚度的端盖，参数见表6，(8)式的计算结果与试验结果对比如图9所示。可以发现每种端盖厚度条件下公式计算结果均与实验结果吻合较好，所提公式及黄广炎等公式与试验结果的误差比较如图10所示。可以发现(8)式最大相对误差仅为6.8%，平均相对误差仅为1.5%，相对文献[9]公式误差显著减小，表明所提公式具有足够的精度。

表6 试验样本参数

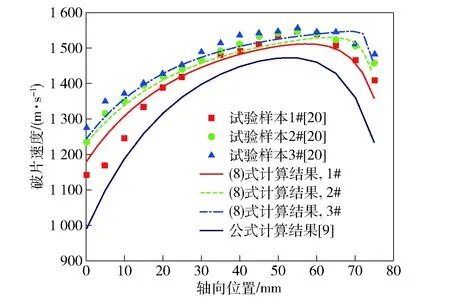
图9 试验结果[20]与计算结果对比图Fig.9 Comparison between calculation results and experimental data[20]

图10 计算结果相对试验结果的相对误差图Fig.10 Relative error between experimental data and calculation results

为验证所提公式适应于不同材质的炸药和材料，采用前人的两项试验结果进行验证。其中试验No.9302中炸药和壳体材料为Octol和1020钢，壳体为预制破片，长径比为2，=0.93，两端无端盖；No.9457中炸药为Octol，壳体为1020预制破片，内含有1.6 mm厚的6061-T4铝合金衬套，端盖为2024-T3铝合金，厚度6.35 mm，具体试验参数如表7所示，详情见文献[21]中表I。试验结果与(8)式计算结果比较如图11所示。由图11可以发现，对于不同炸药和壳体材质，(8)式均能获得精确的预测结果，相对试验No.9302，(8)式平均相对误差仅为3.13%，产生误差一部分原因是由于壳体采用预制破片后壳体会提前断裂导致爆轰产物提前泄露造成破片速度低于整体型壳体产生的自然破片速度；相对试验No.9457，预制破片内侧放置了1.6 mm厚的6061-T4铝合金衬套，使得爆轰产物不至于过早泄露，因此(8)式得到的计算结果与试验结果相比平均误差仅为0.46%，且试验证明了(8)式可适应于端盖与壳体不同材质，证明了公式中所提无量纲参数和的合理性。

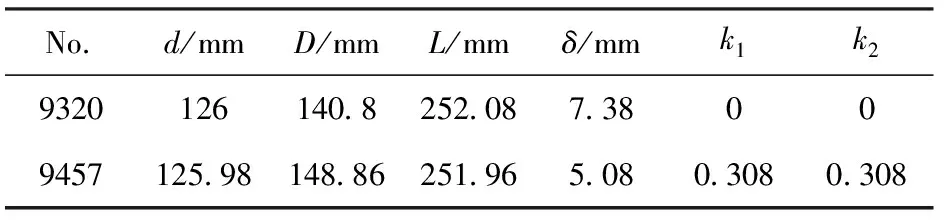
表7 试验参数

图11 试验结果[21]与公式计算结果比较图Fig.11 Comparison between calculation results and experimental data[21]

同时，为了验证两端端盖厚度不会影响另一端端盖附近的破片初速分布，采用上述经过试验验证的仿真模型，设计了两端带有不同厚度端盖的圆柱形装药壳体模型来进行验证。壳体和装药材料与先前的一致。仿真模型参数如表8所示。仿真结果和(8)式的计算结果对比如图12所示，可以发现虽然两端端盖厚度不同，但是公式计算结果仍然与仿真结果具有很好的一致性，说明无论两端的端盖厚度是相同还是不同，一端端盖的厚度不会影响另一端破片初速分布。

表8 验证仿真参数

通过以上试验结果和仿真结果的比较表明，所提的破片初速公式能够较准确地预测端盖厚度对圆柱形装药壳体破片初速的影响。

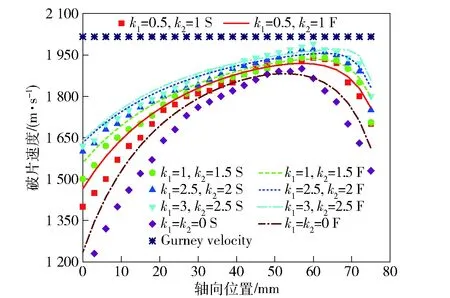
图12 计算结果与仿真结果对比图Fig.12 Comparison between simulation and calculation results

4.3 讨论

图13是不同端盖厚度条件下(8)式计算得到的破片初速分布，其中壳体和装药材料与上述材料一致，尺寸为：=90 mm，=36 mm，=44 mm。

由图13可以发现，随着端盖厚度的增加，轴向稀疏波对两端破片的影响逐渐减小，两端破片初速逐渐接近格尼速度；当非起爆端端盖厚度是壳体厚度5倍以上(≥5)时，轴向稀疏波的影响基本被端盖作用抵消，非起爆端破片初速基本达到格尼速度；当起爆端端盖厚度是壳体厚度10倍以上(≥10)时，轴向稀疏波对起爆端破片的影响范围相对无端盖时的影响范围缩减到10%以内(<0.2)，破片基本达到格尼速度；端点处(=0,=)破片初速偏低是由于其同时处于端盖上，端盖的等效装填比小，因此速度会偏低，但仅仅是一点位置处速度偏小，对速度分布的影响可忽略。

目前的治疗疫苗虽然种类繁多，但由于癌变后病情较为复杂、多变，目前的HPV治疗性疫苗并不能达到理想的免疫治疗效果。

因此(8)式的实际应用范围：0≤≤10,0≤≤5，如(21)式所示，端盖厚度超过此范围后可直接采用格尼公式计算。同时实际应用中战斗部两端端盖厚度为有限厚度，因此(8)式对于战斗部有效破片数的计算及毁伤效能分析具有十分重要的实际应用价值。同时，两端端盖厚度的关系也间接验证了起爆端轴向稀疏波的影响范围是非起爆端轴向稀疏波影响范围的2倍。

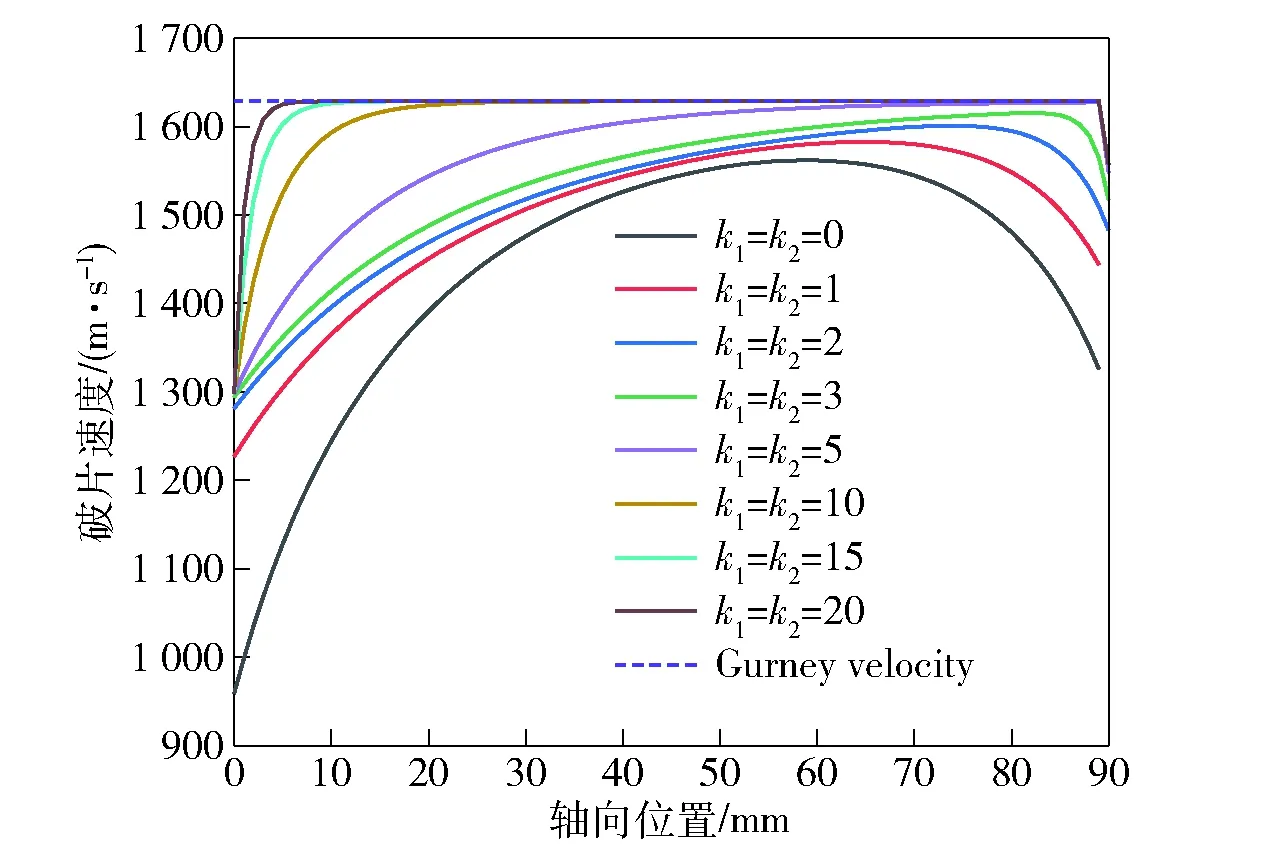
图13 不同端盖厚度圆柱形装药壳体破片初速分布Fig.13 Initial velocity distribution of fragments from cylindrical charge shell with end caps of different thicknesses

5 结论

本文针对不同厚度端盖对圆柱形装药壳体破片初速的影响，采用理论和仿真计算的方法进行了量化分析。得到主要结论如下：

1)建立带不同厚度端盖的圆柱形装药壳体仿真模型，并基于试验数据，验证了模型的合理性。

2)仿真分析得到端盖对破片加速过程影响规律：随着端盖厚度的增加，轴向稀疏波作用递减，两端破片速度相应增加，相对起爆端破片非起爆端破片加速更明显；冲击波加速能量的增加是造成起爆端破片初速增加的主要因素，非起爆端破片初速增加则更多归功于爆轰波加速能量的增强。

3)建立了可预测不同厚度端盖的圆柱形装药壳体破片初速分布理论公式，并通过仿真确定了关键参数，公式适应范围为：0≤≤10,0≤≤5，当超出上限值，轴向稀疏波对端部破片初速的影响基本忽略，即两端破片基本达到格尼速度。试验对比结果表明公式可以适应不同材料的壳体和炸药，相对前人公式误差显著减小，其对杀伤战斗部提高有效破片数和毁伤效能评估具有实际的指导价值。

[1] STRONGE W J, MA X, ZHAO L. Fragmentation of explosively expanded steel cylinders[J]. International Journal of Mechanical Sciences, 1989, 31(11/12): 811-823.

[2] 李铁鹏. 战斗部破片初速分布及空间数量分布[D]. 南京：华东工学院, 1988.

LI T P. The distribution of warhead fragment muzzle velocity and space quantity[D]. Nanjing：East China Industrial Engineering Institute, 1988. (in Chinese)

[3] 王志军, 尹建平. 弹药学[M]. 北京：北京理工大学出版社, 2005.

WANG Z J, YIN J P. Ammunition[M]. Beijing: Beijing Institute of Technology Press, 2005. (in Chinese)

[4] GURNEY R W. The initial velocities of fragments from bombs, shell, grenades[R]. BRL Report 405, 1943.

[5] BOLA M S, MADAN A K, SINGH M, et al. Expansion of metallic cylinders under explosive loading[J]. Defence Science Journal, 2013, 42(3): 157-163.

[6] GAO Y G, FENG S S, ZHANG B, et al. Effect of the length-diameter ratio on the initial fragment velocity of cylindrical casing[J]. IOP Conference Series Materials Science and Engineering, 2019, 629(1): 012-020.

[7] 冯顺山, 崔秉贵. 战斗部破片初速轴向分布规律的实验研究[J]. 兵工学报, 1987, 11(4): 60-63.

FENG S S, CUI B G. An experimental investigation for the axial distribution of initial velocity of shells[J]. Acta Armamentarii, 1987, 11(4): 60-63. (in Chinese)

[8] 印立魁， 蒋建伟， 门建兵，等. 立方体预制破片战斗部破片初速计算模型[J]. 兵工学报, 2014, 35(12): 1967-1971.

YIN L K, JIANG J W, MEN J B, et al. An initial velocity model of explosively-driven cubical fragments[J]. Acta Armamentarii, 2014, 35(12): 1967-1971. (in Chinese)

[9] HUANG G Y, LI W, FENG S S. Axial distribution of Fragment Velocities from cylindrical casing under explosive loading[J]. International Journal of Impact Engineering, 2015, 76: 20-27.

[10] KONG X, WU W, LI J, et al. A numerical investigation on explosive fragmentation of metal casing using Smoothed Particle Hydrodynamic method [J]. Materials and Design, 2013, 51(60): 729-741.

[11] GUO Z W, HUANG G Y, ZHU W, et al. Mechanism and suppression of the effect of axial rarefaction waves on the eccentric initiation effect [J]. International Journal of Impact Engineering, 2018, 124: 37-47.

[12] GAO Y G, FENG S S, YAN X M, et al. Axial distribution of fragment velocities from cylindrical casing with air parts at two ends [J]. International Journal of Impact Engineering, 2020, 140: 44-57.

[13] RANDLES P W, LIBERSKY L D. Smoothed particle hydrodynamics: some recent improvements and applications[J]. Computer Methods in Applied Mechanics & Engineering, 1996, 139(1-4): 375-408.

[14] RABCZUK T, EIBL J. Modelling dynamic failure of concrete with meshfree methods[J]. International Journal of Impact Engineering, 2006, 32(11): 1878-1897.

[15] HAYHURST C J, CLEGG R A. Cylindrically symmetric SPH simulations of hypervelocity impacts on thin plates[J]. International Journal of Impact Engineering, 1997, 20(1-5): 337-348.

[16] 张雁思, 戴文喜, 王志军. 基于SPH算法的爆破战斗部壳体破碎数值仿真研究[J]. 兵器材料科学与工程, 2015,38(5): 85-88.

ZHANG Y S, DAI W X, WANG Z J. Numerical simulation of blasting warheads shell breaking based on SPH method[J]. Ordnance Material Science and Engineering, 2015, 38(5): 85-88. (in Chinese)

[17] LI W, HUANG G Y, FENG S S. Effect of eccentric edge initiation on the fragment velocity distribution of a cylindrical casing filled with charge[J]. International Journal of Impact Engineering, 2015, 80: 107-115.

[18] 陈刚,陈忠富,陶俊林,等.45钢动态塑性本构参量与验证[J]. 爆炸与冲击, 2005, 25(5): 69-74.

CHEN G, CHEN Z F, TAO J L, et al. Investigation and validation on plastic constitutive parameters of 45 steel [J]. Explosion and Shock Waves, 2005,25(5): 69-74. (in Chinese)

[19] DYNAMICS C. Release 14.0 documentation for ANSYS AUTODYN[Z]. US: ANSYS Inc., 2011: 150-151.

[20] LIAO W, JIANG J W, MEN J B, et al. Effect of the end cap on the fragment velocity distribution of a cylindrical cased charge[J]. Defence Technology, 2020, 17(3): 1052-1061.

[21] PREDEBON W W, SMOTHERS W G, ANDERSON C E. Missile warhead modeling: computations and experiments[R]. 1977, ADA047294.