参数化时频分析在连续波有源探测中的应用

薛城， 顾怡鸣， 宫在晓， 李整林,3

(1.中国科学院声学研究所 声场声信息实验室， 北京 100190； 2.中国科学院大学， 北京 100049；3.中山大学海洋工程与技术学院， 广东 珠海 519000)

0 引言

在传统主动声呐探测应用场景中，大多使用脉冲式主动声呐(PAS)。传统PAS模式的优点是工作方式相对简单，但存在一些明显的缺点，如发射功率高，目标照射时间短，探测更新周期长等。针对上述问题，近年来，国内外开始重视连续波主动声呐(CAS)技术的研究工作，并取得了一些进展。与传统的PAS相比，CAS模式具有处理增益大，抗干扰能力强，目标跟踪更新率高等优势。相对的，CAS对发射信号的波形设计和处理方法也有更高的要求：一是要兼顾目标更新速率和时间带宽增益，二是要考虑到CAS工作在多基地模式下的多源互扰问题。

受连续波雷达领域的影响，连续波探测技术最初应用于水声探测领域时，通常以线性调频连续波信号(LFMCW)作为发射信号。随后，Costas序列、连续单频信号、正弦调频信号等波形被相继应用于CAS波形设计，以提高目标主动探测的更新速率。Murphy等首先提出了CAS的子带滤波处理方法，将线性调频信号划分若干子带进行匹配相关处理，可以提高更新速率，但相应降低了输出信噪比。刘大利等将差拍- 分数阶傅里叶算法用于CAS的检测，可以消除LFMCW的距离- 速度耦合现象，获取较高的时间带宽增益，但没有考虑更新速率问题，且无法适用于其他调频信号。张烈山等在差拍信号的基础上引入空气超声信号作为参考信号，对水声差拍信号进行重采样以提取主频，实现了对非线性调频连续波信号的测距，但由于引入了空中和水下两路换能器，对应用环境有较高的要求。

双曲调频(HFM)信号是一种具有多普勒不变性的调频信号。相比线性调频信号，HFM信号的宽带多普勒不敏感性质使得其对运动目标的检测具有独特优势，在声呐回波处理过程中不需要进行细致的多普勒补偿，减少了运算量，因此广泛应用于水下有源探测领域。但是，目前传统CAS系统的信号处理方法多基于LFMCW模型，不能直接适用于其他形式的连续波信号，针对HFM信号的目标识别、定位问题需要更深入的研究。

对于类似HFM连续波信号的长时非平稳信号，单独的频域或时域分析方法只能获取有限的信号信息，无法兼顾信号在时域和频域的整体特征。因此，各类时频分析工具被引入水声信号处理中，以对接收信号进行时频特性的分析，如短时傅里叶变换、小波变换、维格纳- 威尔分布和短时分数阶傅里叶变换等。但是，上述非参数化时频分析方法均在一定程度上将信号假定为局部平稳信号，并采用固定的时频分析窗，这导致了它们对强时变或强频散信号的分析能力较差。而参数化时频变换根据信号模型构造与之匹配的变换核，将信号在时频表示中的能量集中于变换核附近，可以准确地获取非平稳信号的局部特征。相应的，参数化时频分析的性能与变换核参数的选取密切相关，设计出与声呐信号对应的变换核函数是将参数化时频分析应用于CAS信号处理的关键。

本文针对CAS系统中双曲调频连续波信号的检测问题，研究并提出了一种基于参数化时频变换的信号处理方法。算法结合参数化时频分析思想，根据CAS信号模型，设计针对HFM信号形式的变换核函数，从而获取集中度最高的时频表示，提升目标检测性能。同时，基于参数化时频分析算法可以通过旋转时频滤波分离声呐接收信号中的回波与直达波分量，从而达到抑制直达波干扰的效果，改善弱回波的检测性能。通过仿真和海上试验验证了该算法在双基地连续波有源探测中的可行性和有效性。

1 信号模型

双基地模式的双曲调频CAS系统，通过周期发射HFM信号，分析接收端回波信号，进行目标检测和定位。在一个扫频周期内，发射信号可以表示为

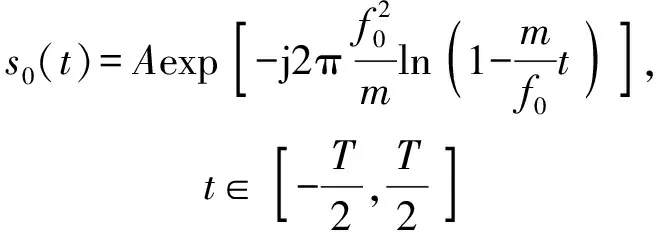
(1)

式中：为发射信号幅度；为信号时间中心频率；为信号频率变化率，=，为双曲调频渐进时间；表示脉冲时间宽度。发射信号的瞬时频率可以表示为

(2)

假设发射端与接收端静止不动，当存在一个距离发射端，距离接收端的运动目标时，单个发射周期内的目标回波信号可以表示为

(3)

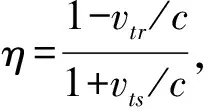
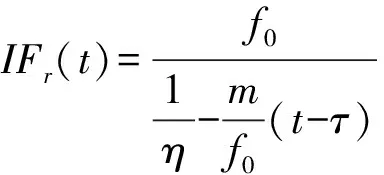
(4)

由于HFM信号具有多普勒不变性，在常规水声探测场景下，可以将HFM信号的多普勒压缩或拓展效应等效为频率调制函数在时间上的平移，因此回波信号的瞬时频率的变化规律不变，即

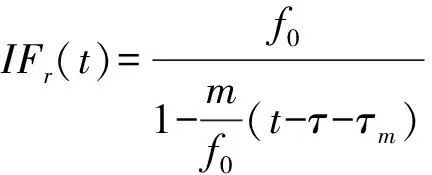
(5)

在双基地模式下，接收信号中还存在直达波分量，与(4)式类似，可以得出单个发射周期内的直达波瞬时频率为

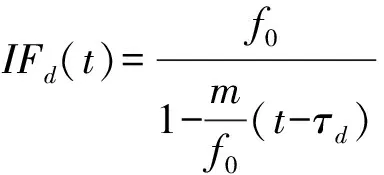
(6)

式中：=，为发射端到接收端的距离。包含回波和直达波的接收信号时频分布示意图如图1所示。

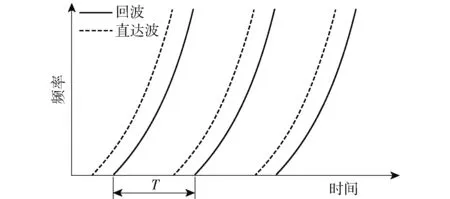
图1 CAS接收信号时频分布示意图Fig.1 Time-frequency distribution of CAS received signals

2 参数化时频分析理论与处理方法

基于参数化时频分析的信号处理主要流程如图2所示。首先对接收信号进行带通滤波和波束形成以获取阵列增益，然后通过参数化时频分析得到波束输出的时频表示，其变换核参数可由发射信号参数确定。对时频分布功率谱进行阈值滤波提取时频分布内的脊线，获取非相干累加输出进行峰值检测，并获取时频特征参数。滤波阈值和检测门限的设置可采用恒虚警检测技术根据背景噪声级调整。在得到时延和时频曲线等估计值后，再结合双基地有源探测定位方法，可进行目标定位。以下分别对时频分析方法，核函数设计方法和直达波干扰抑制方法开展讨论。

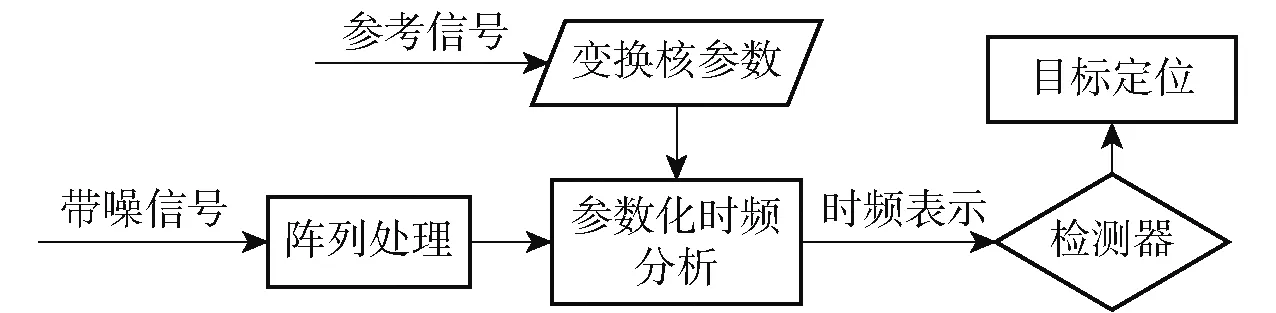
图2 HFM连续波信号处理流程示意图Fig.2 Flow chart for HFM continuous wave signal processing

2.1 参数化时频分析原理

广义参数化时频变换(GPTF transform)是由杨扬等在多种参数化时频变换基础上总结归纳而来，其定义如下：

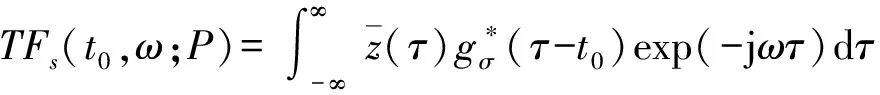
(7)

式中：

(8)

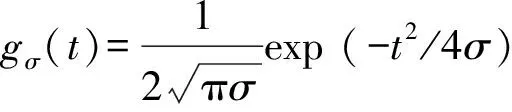
不失一般性，假设某信号的解析信号为：

(9)

其瞬时频率为时间的函数()。如图3所示，对()进行的如(7)式定义的参数化时频变换，其过程可简述为：首先在时频面内对信号做旋转变换，即将目标信号的时频特征()减去核函数()；然后在时频面内做平移变换，即将信号上移处的频率增量()；最后在附近加窗函数()对信号做短时傅里叶变换。参数化时频变换结果的频域分辨率由两部分决定：加窗信号旋转后的带宽Δ(;)和窗函数频带宽1。如果能构造恰当的核函数，使()-()在任意时刻均为一常数，即Δ(;)≡0，则可使得频域分辨率始终为1，从而得到能量集中度最高的时频表示。由此可见，变换核参数直接决定了参数化时频分析的频域分辨率，准确获取时频特征的关键就是构造与信号相匹配的变换核()。即令

()=()+

(10)

其中为一频延常数，如(7)式的参数化时频变换可以准确刻画一类非平稳信号的时频特征，其瞬时频率的时变特征为()。

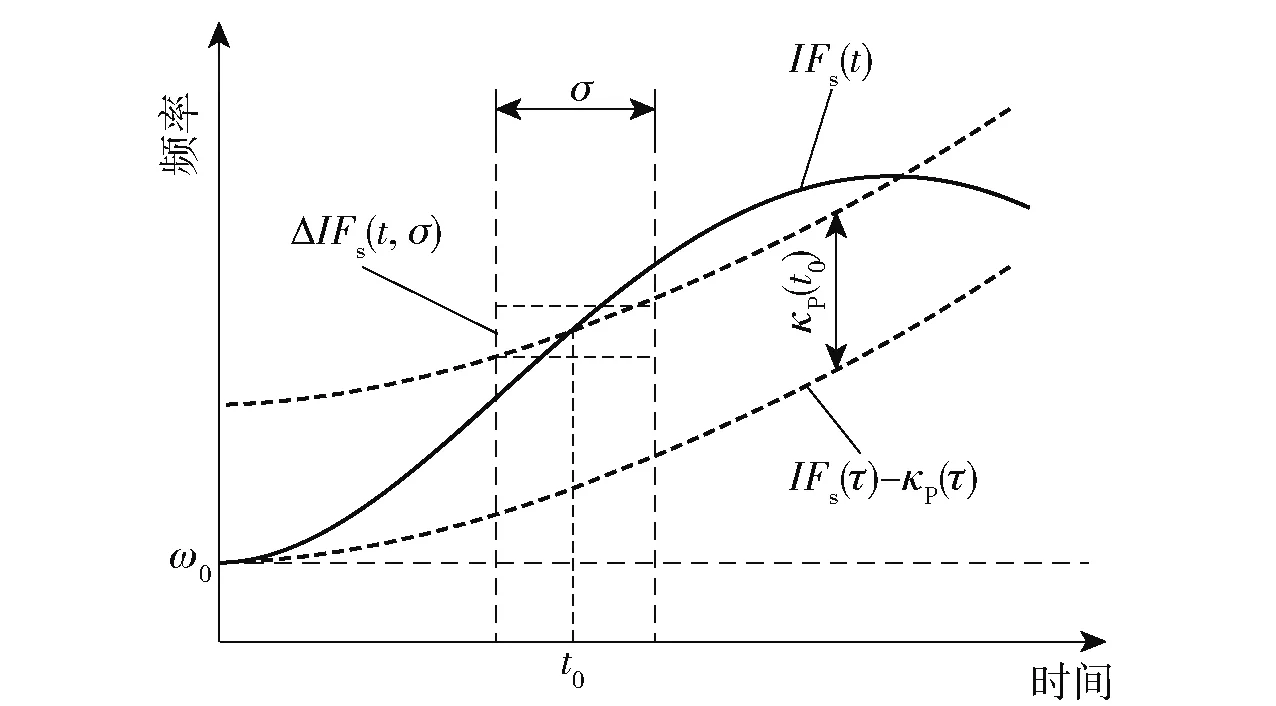
图3 参数化时频分析原理示意图Fig.3 Schematic diagram of parametric time-frequency analysis

2.2 针对双曲调频CAS的核函数设计

在工程信号等领域的应用中，参数化时频分析的核函数设计往往使用时频特征逼近原理。首先选取某类泛用形式的非线性变换核，如多项式函数或样条函数等，再以此变换核对目标信号进行多次循环逼近求精，从而得到最适合的变换核参数。这种方法需要人为选择拟合函数，迭代计算量大，且不能直接用于多分量信号，对水声探测适用性较差。基于连续波有源声呐收发系统的特性和HFM的时频特征，以下提出一种针对CAS系统中HFM信号的核函数设计方法。

由(4)式和(5)式可知，CAS接收信号具有相干信号模型的特点，回波分量和直达波分量都具有与发射信号相同的瞬时频率变化规律，且瞬时频率函数仅相差一个时延量，即()=(--)。针对上述特点，根据时频域的对偶性，将广义参数化时频变换的定义转换至频域形式，如下式：

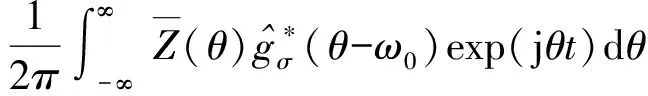
(11)

式中：

(12)

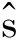
同样的，频域参数化时频分析的关键在于确定核函数。与式(10)类似，假设一个信号的瞬时频率函数()的反函数(即局部频率延迟函数)()，则当核函数()=()+时，时频表示分辨率可以达到最优，其中为一时延常数。

由(5)式可得，HFM信号的局部频率延迟函数为

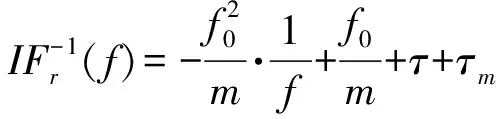
(13)

因此，只要取核函数

(14)

根据发射信号参数构造频域形式的核函数，可使得参数化时频分析能同时处理包含多个相干分量(如多个目标回波或直达波)的HFM接收信号，获取接收信号的整体时频表示，而不需要进行逐次滤波或分级计算迭代等操作。得到能量集中度最高的时频表示后，在时频域内沿时间轴或频率轴进行阈值滤波，获取脊线坐标，即可估计接收信号的真实时频特征。

2.3 基于参数化时频分析的直达波抑制

在CAS系统中，由于采用双基地模式，发射信号会直达接收阵列，直达波的能量通常远高于回波信号。同时受到海洋信道多途效应等因素的影响，直达波的旁瓣往往会掩蔽回波分量，导致回波检测性能的下降。因此在对回波分析前，需要考虑将直达波分量分离滤除，以消除其影响。

基于参数化时频分析的接收信号分量分离，基本思想与广义解调时频分析方法类似。根据定义，在参数化时频分析中，旋转算子的作用是在时频面上将信号的时频特征进行旋转，而平移算子的作用是将信号的能量平移至其真实时频特征的脊线位置。若不加平移算子，频域的参数化时频变换的数学表示退化为

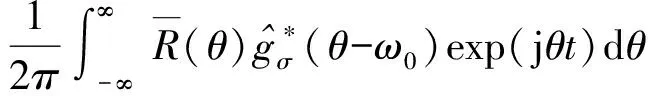
(15)

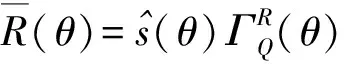
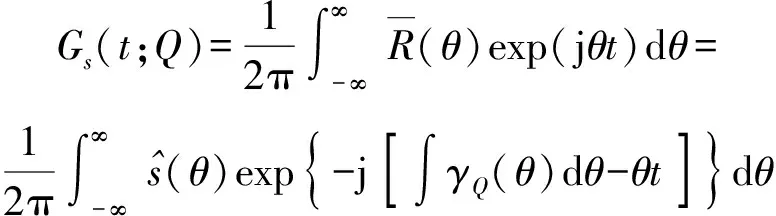
(16)

上式的逆变换为

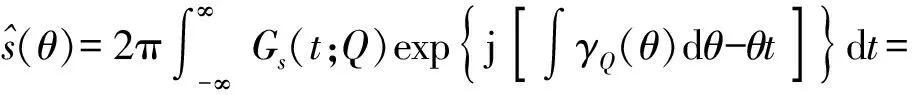
(17)

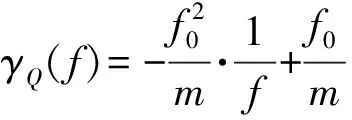
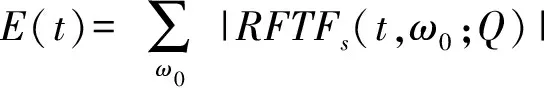
(18)

并通过局部输出峰值确定回波接收时延，

(19)

再以此时延为中心对时频表示进行带通滤波，则可得到只包含该信号分量的旋转时频表示：

(20)

式中：为根据时频分辨率确定的时间窗大小。当信号段内仅存在单个周期直达波或回波时延不能准确确定时，也可采用以直达波接收时延为中心进行带阻滤波的方法，即

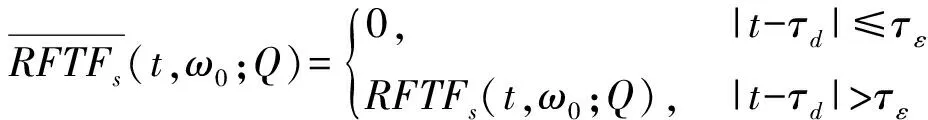
(21)

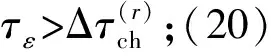
针对分离出的回波信号波形，可以进一步进行分析处理以实现匹配或定位等目的。当存在多个水下目标时，此算法同样可以用于分离来自不同目标的相干信号分量，逐个获取回波参数，从而对多个目标回波进行处理。同时，由于参数化时频分析方法不涉及接收指向性，因此可以与空域滤波等方法相结合，进一步抑制直达波干扰。

3 仿真与实验数据验证

本节首先通过仿真数据检验参数化时频分析方法的可行性，并与传统CAS信号处理算法进行比较。仿真条件参考南海浅海实验环境与部署情况，环境噪声为高斯白噪声，声速剖面为双负跃层，海底模型采用半无限液态海底，如图4所示。然后，对南海浅海双基地声呐有源探测实验数据进行分析，利用实验数据验证参数化时频分析方法的检测性能和直达波干扰抑制效果。

图4 实验部署及环境参数示意图Fig.4 Experimental setup and environmental parameters

3.1 仿真分析

311 参数化时频分析与子带滤波性能对比

在参数化时频变换过程中，由于白噪声在时频平面上均匀分布，在时频表示中不会出现聚集峰。理想情况下，参数化时频分析对HFM信号的理论处理增益为

(22)

式中：为信号带宽；Δ为时频分析中的高斯窗频宽；Δ为对应的时域长度；10lg (2ΔΔ)对应加窗部分时频表示增益；10lg (Δ)对应沿频率轴累加获得的非相干增益。可以看出，上式的形式与子带滤波方法的理论增益公式相同。

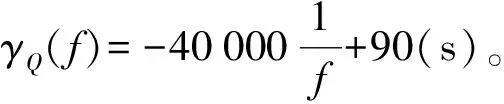
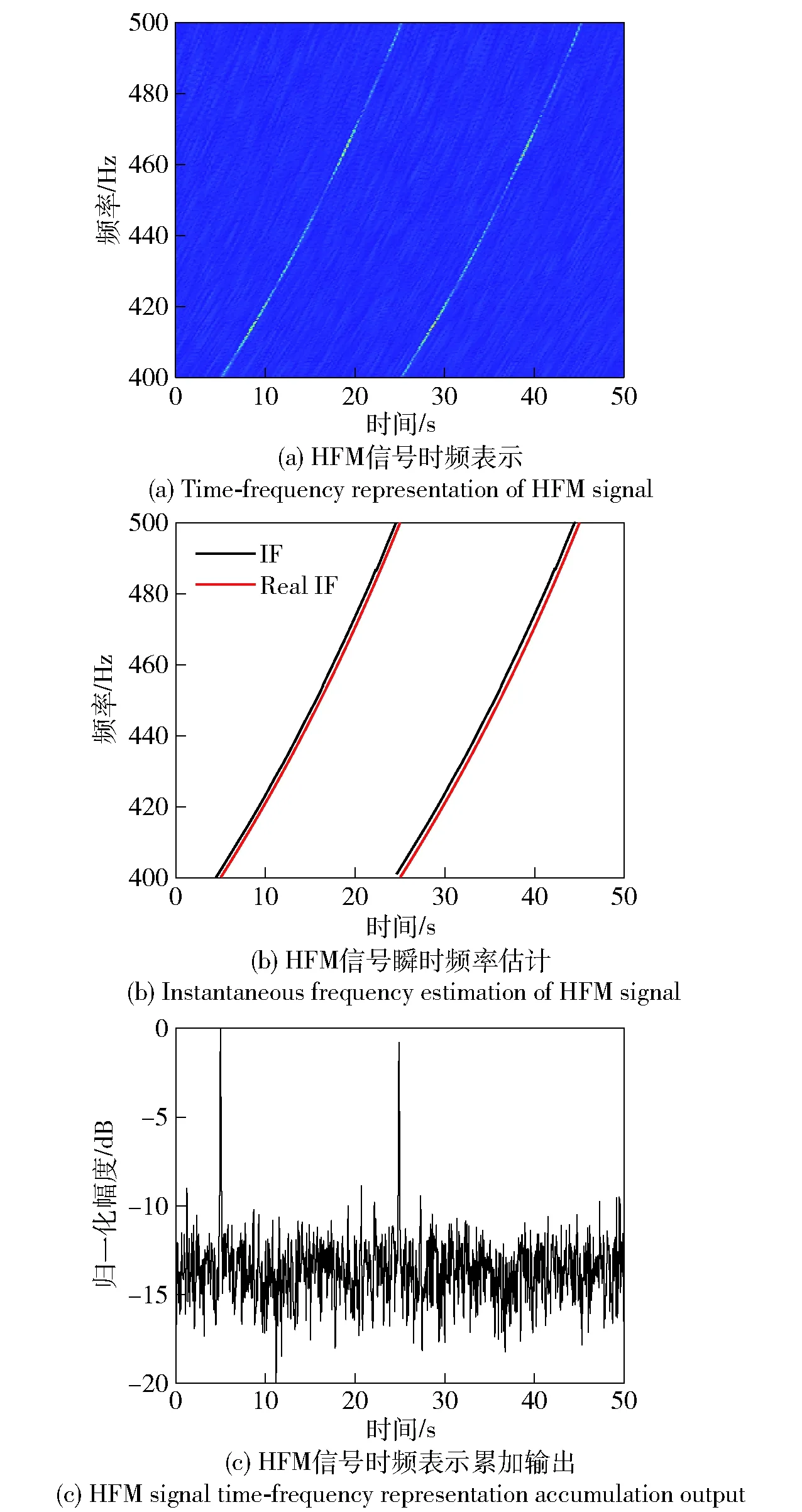
图5 HFM连续波信号参数化时频分析结果Fig.5 Parameterized time-frequency analysis of HFM continuous wave signal

作为对比，使用传统CAS子带滤波方法处理上述仿真数据，采用频域子带分割方式将接收信号分为5个子带，子带带宽均为20 Hz。子带信号经过带通滤波处理后，分别与对应的子带参考信号进行相关处理，得到相关峰。最后设置检测门限，同样以多子带的非相干累加峰值作为信号检测依据，如图6所示，图中峰值信噪比约为13.3 dB，相对信噪比增益约28.3 dB。

图6 HFM连续波信号子带滤波输出Fig.6 HFM continuous wave signal sub-band filter output

使用蒙特卡洛统计方法多次重复上述仿真，对比不同信噪比条件下，两种算法的实际信噪比增益，结果如图7(a)所示，其中每个信噪比下仿真次数为500次，且目标运动速度随机。结合理论增益公式可以看出，在相同噪声环境条件下，当时频分析的高斯窗长度与子带滤波的子带带宽相同时，两种算法的理论增益上限相同；但对HFM信号来说，子带滤波方法采用时域或频域的平均分割时，每个子带内的时间带宽积10lg (2Δ·Δ)并不完全相同，因此总体信噪比增益低于参数化时频变换算法。对于相同带宽和脉宽的.HFM信号，双曲调频深度=(2)越大，则子带之间的差异越大，上述信噪比增益的差距也越大。

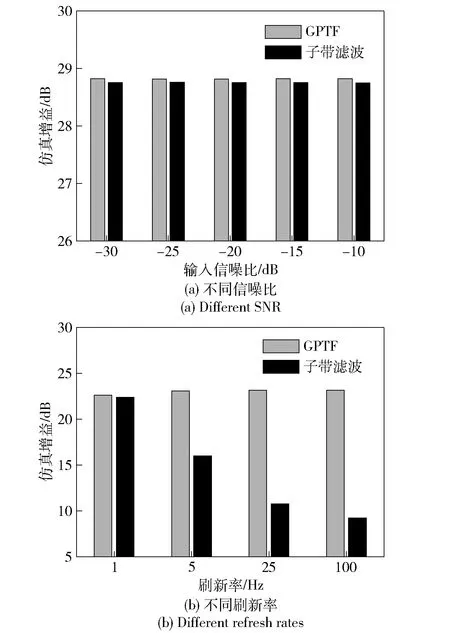
图7 仿真信号处理结果对比Fig.7 Comparison of simulation signal processing results

另一方面，子带滤波方法的目标跟踪刷新率与子带宽度呈反比，因此刷新率与处理增益存在着相互制约的关系，即=1Δ；而参数化时频分析的目标跟踪刷新率不受子带宽度制约。同样采用蒙特卡洛统计方法，仿真目标跟踪刷新率变化时，两种算法的实际信噪比增益，结果如图7(b)所示，其中接收信噪比均取-15 dB，每个刷新率下仿真次数为500次。从图7(b)中可以看出，当减小子带宽度，提高目标刷新率时，子带滤波的时间带宽积减小，处理增益会相应降低；而参数化时频分析方法的处理增益基本保持不变，因此可以在保证信噪比增益的同时获取如图5(b)的高分辨率时频特征曲线，性能上优于子带滤波算法。

除信噪比增益外，峰值旁瓣比等因素也会影响声呐接收机检测性能。因此使用虚警概率和检测概率曲线进一步对比两种算法检测性能，在上述仿真基础上，使用蒙特卡洛统计方法，分析两种方法的CAS检测性能，并绘制出接收机工作特性曲线，结果如图8所示。图8中给出了恒虚警条件下两种方法的检测概率曲线。从图8中可以看出：当虚警概率为0.1%时，在-22 dB信噪比下，参数化时频分析可以达到99%以上的检测概率，而子带滤波只有92%左右的检测概率；当虚警概率为0.01%时，在-22 dB信噪比下，参数化时频分析仍可达到96%的检测概率，而子带滤波的检测概率仅有71%。在相同信噪比条件下，参数化时频分析方法的检测性能优于子带滤波算法。

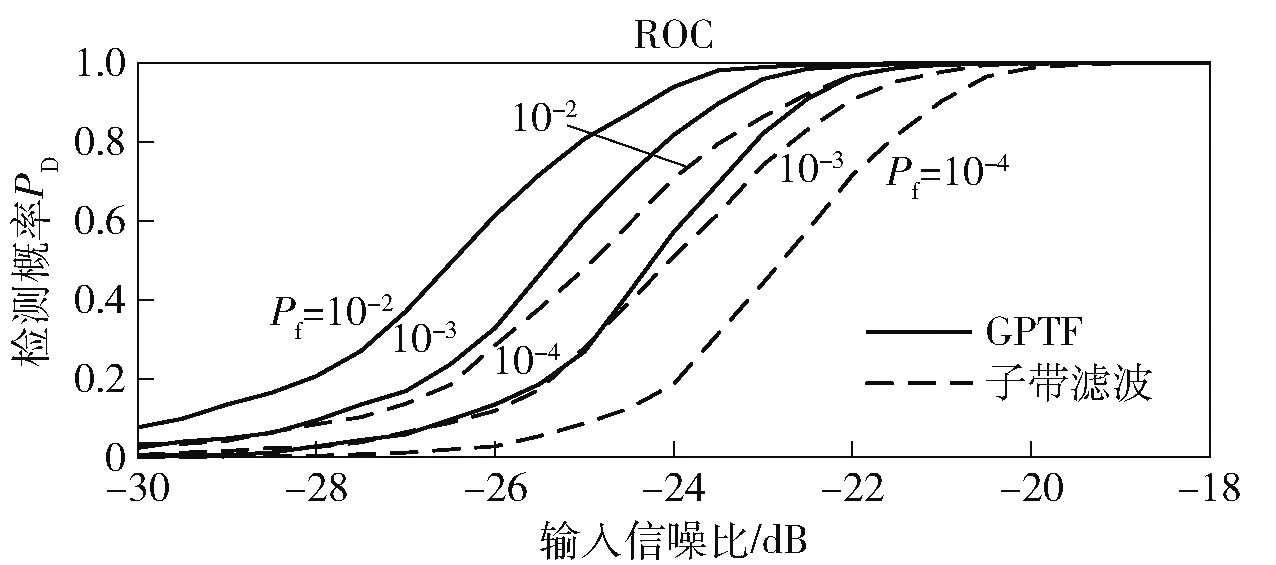
图8 CAS接收机工作特性曲线Fig.8 Operation characteristic of the CAS receiver

以上仿真结果表明，参数化时频分析方法能够有效检测HFM连续波信号，并准确估计其时频特征，有效提高了连续波声呐系统的检测性能。

3.1.2 直达波干扰抑制仿真

为了验证参数化时频分析方法对主动声呐直达波干扰抑制的有效性，在上述仿真条件基础上增加直达波干扰。假设目标为静止状态，声呐发射端与接收端距离6 km，回波接收信噪比为-3 dB，HFM信号参数和其他环境条件不变。

图9(a)为接收信号的参数化时频分析结果。其时频表示内包含两个周期内直达波分量与回波分量的峰值脊线，分别对应两个分量的瞬时频率曲线。在仿真条件下，当不考虑直达波的接收指向性增益时，目标回波相对直达波干扰的信干比接近-30 dB，此时难以在时频表示中有效提取回波的瞬时频率曲线。图9(b)显示了对接收信号进行的参数化旋转时频变换结果，对应信号分量的脊线变为垂直于时间轴的直线。图9(c)给出了在旋转时频域中将时频表示沿频率轴积分得到的非相干增益结果，通过其峰值坐标可以得到直达波和目标回波分量的接收时延，其中第一个发射周期内直达波和回波信号峰的对应时延分别为3.95 s和4.98 s。

图9 仿真接收信号参数化时频分析结果Fig.9 Parameterized time-frequency analysis results of the simulated received signal

在旋转时频表示中，以4.98 s为中心进行带通滤波，然后经过旋转时频逆变换，重构出第一周期内目标回波的时域波形，如图10所示。重复以上过程，得到每个周期内的回波时频表示，并叠加分离前的直达波时频曲线，即可得到接收信号的完整瞬时频率曲线，结果如图11所示。上述仿真结果验证了算法对直达波干扰抑制的有效性，算法通过旋转时频变换的性质，将复杂的时频点分选操作转变为时频平面内的带通滤波，可以有效的分离目标回波和直达波分量，便于提取目标信息。

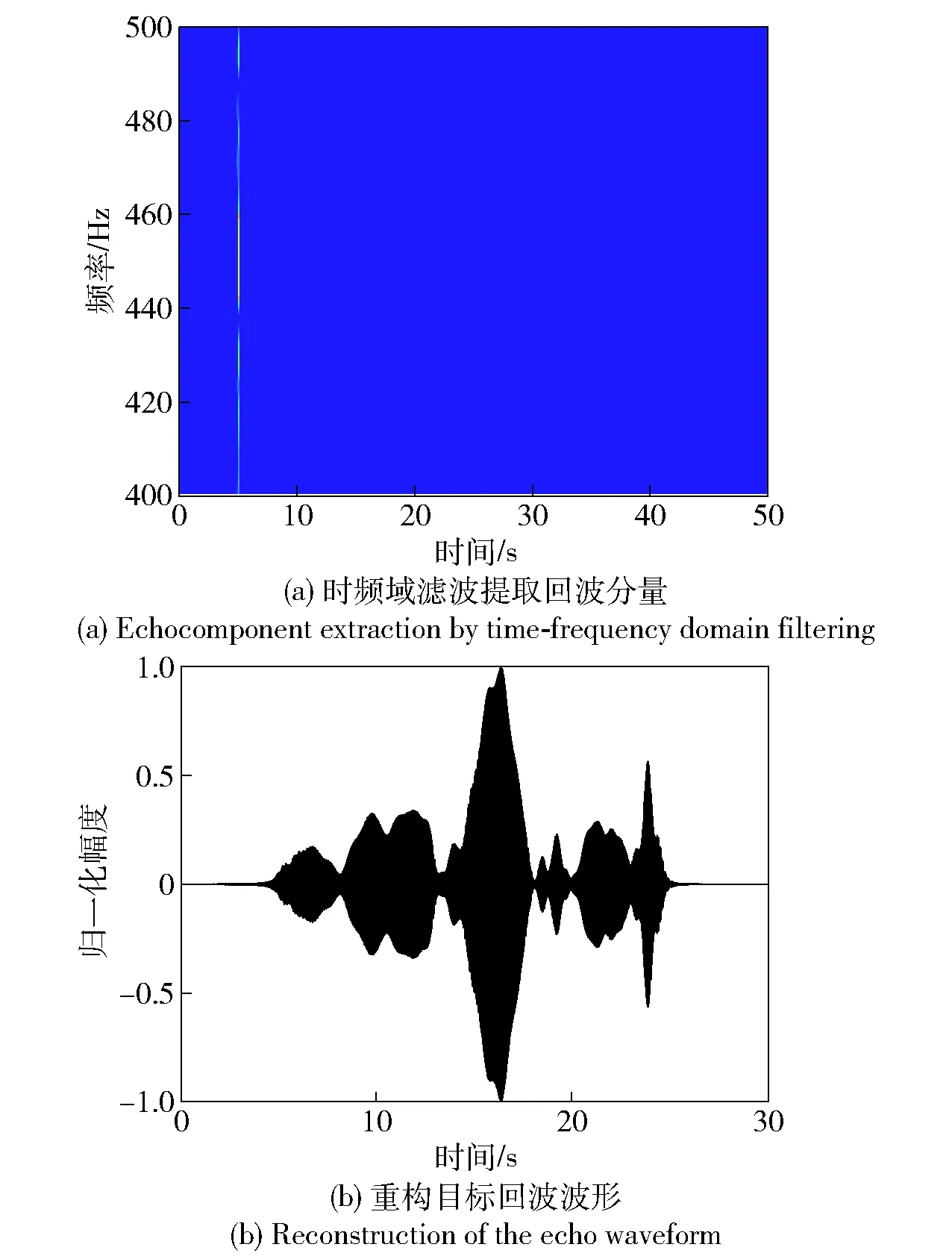
图10 接收信号分量分离与重构Fig.10 Separation and reconstruction of received signal components

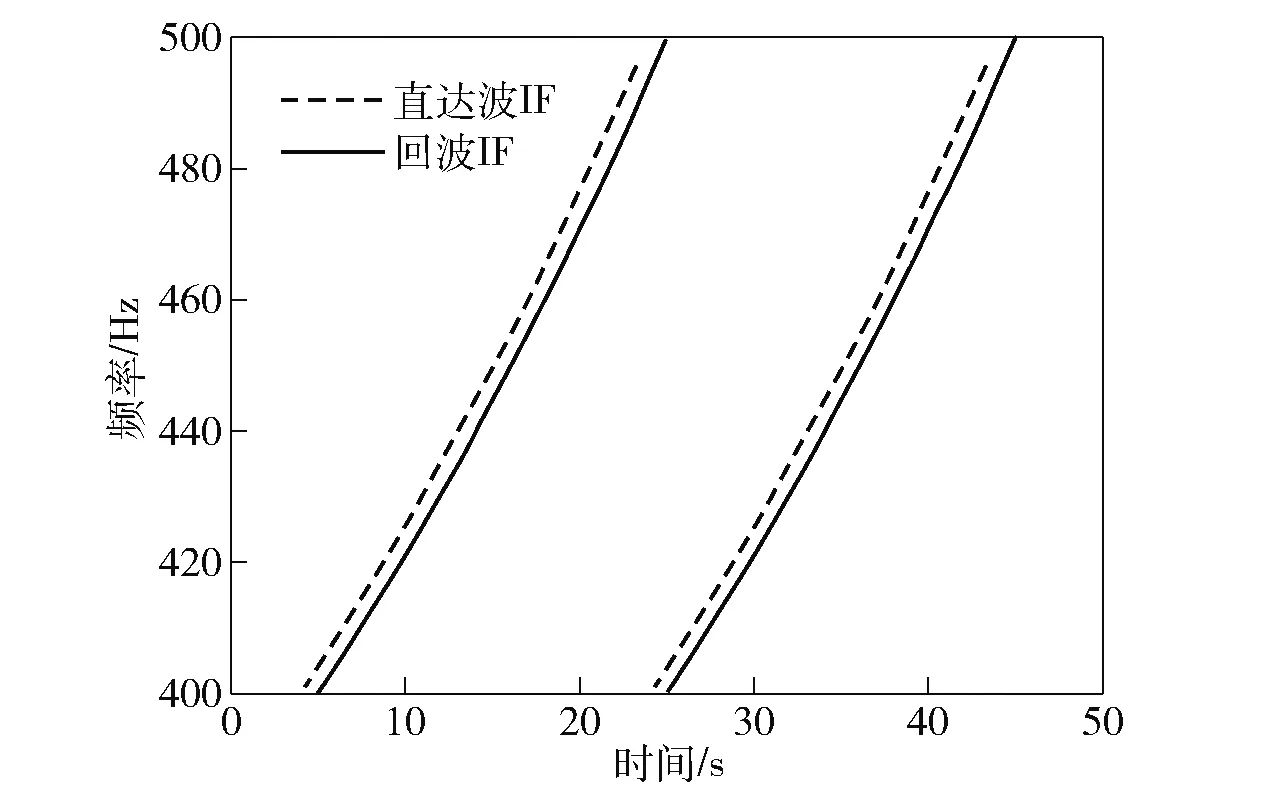
图11 接收信号瞬时频率估计Fig.11 Instantaneous frequency estimation of the received signal

3.2 实验数据分析

为验证上述算法，2018年4月，声场声信息实验室在南海进行了一次浅海有源声呐探测试验。实验采用双基地声呐模式，使用“实验2号”作为发射船，发射声源为吊放换能器，发射信号为带宽100 Hz、脉宽20 s的HFM信号；探测目标为“实验1号”双体船的水下船体部分；以海底水平阵接收信号。实验环境和部署情况如图4所示。实验过程分为4个站位，每站位发射4组HFM信号。实验中，发射船停机漂泊以降低自噪声的影响；目标船沿预定航线低速移动；接收端干扰主要为环境噪声和高强度的直达波。

实验过程中，采用首尾相接的周期发射HFM信号模拟连续波声呐系统。首先对接收信号进行常规波束形成，再对波束输出序列进行分析处理。以发射船相距目标船5.175 km处站位1内第一组接收信号为例，作为对比，图12(a)给出了对未经过直达波抑制的波束输出进行匹配滤波后得到的方位- 时间序列输出，图12(b)则给出了对同一波束输出进行参数化时频变换与累加得到的方位- 时间序列输出，其中0时刻对应信号发射时刻，信号周期发射间隔20 s。从图12中可以看出，直达波干扰的方位约为14°，时频变换结果中的直达波旁瓣相对较窄，但由于目标回波与直达波的到达时间十分接近，直达波造成的掩蔽影响较大，即使经过脉冲压缩或时频分析处理，目标回波仍掩盖在直达波的旁瓣中，无法实现有效的分辨。

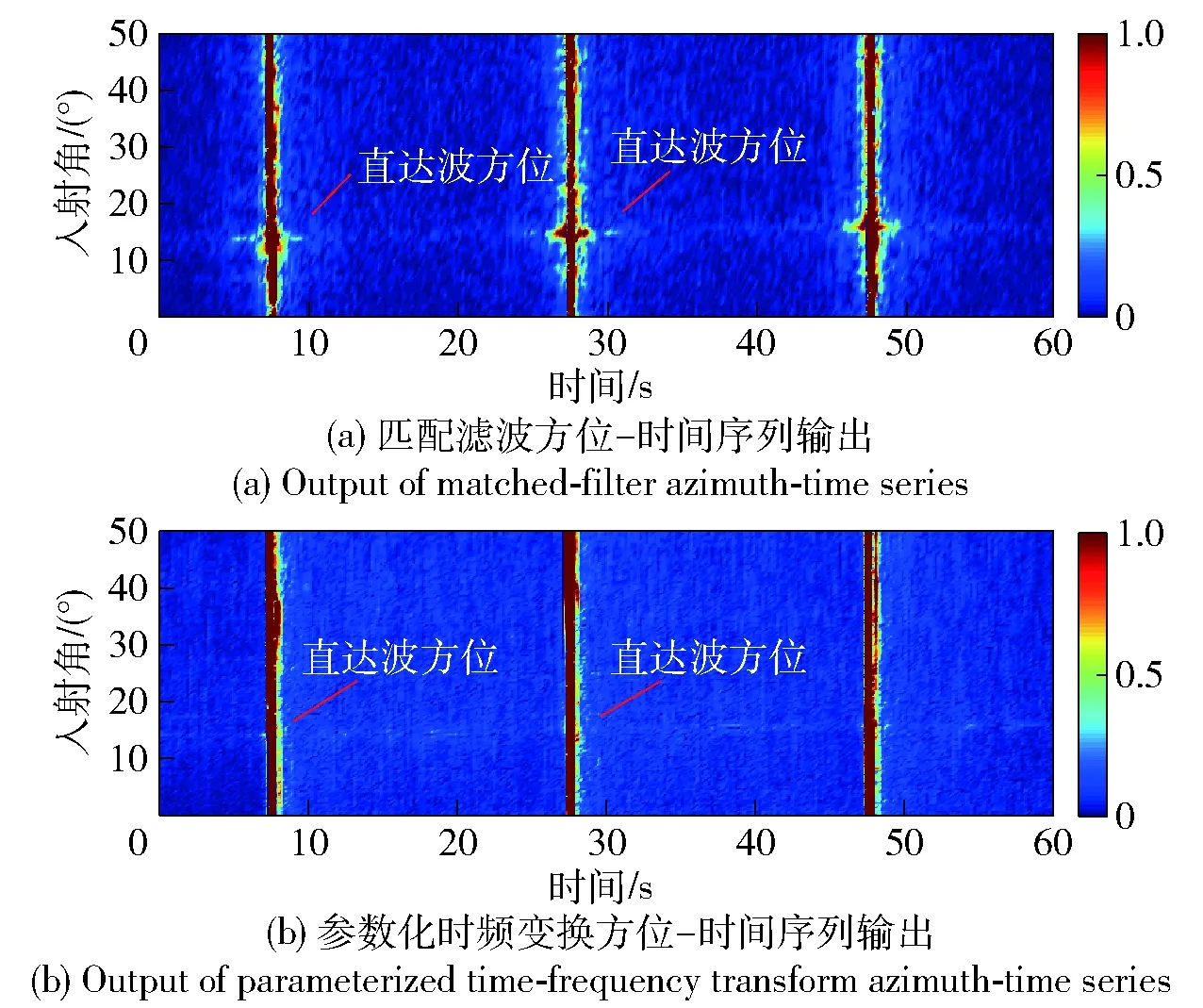
图12 直达波抑制前实验数据波束输出Fig.12 Experimental data beam output before direct wave suppression

然后在参数化时频变换的基础上，对信号波束输出进行直达波抑制处理。图13(a)给出了目标方位波束的参数化时频变换结果，图13(b)、图13(c)分别给出了对应的旋转时频变换结果和第一周期内的时频域累加输出。从输出结果可以得出，此段信号的直达波到达时间为7.24 s，而目标回波接收时间为7.87 s，回波信号峰值位于直达波旁瓣。在旋转时频表示中以7.87 s为中心进行带通滤波后，再经过时频逆变换，即可重构第一周期内回波的时域波形，如图13(d)所示。利用重构的目标回波，通过时频分析可以得出目标回波的瞬时频率曲线，如图13(e)所示。在方位扫描范围内依次进行直达波抑制处理，最后得到时频滤波后的时频分析方位- 时间序列输出如图14所示。对比图14与图12，可以看出，经过旋转时频滤波处理后，直达波干扰被充分抑制，可以清晰分辨第一周期回波所在的方位角为37.4°。

最后结合图13(e)、图14和双基地声呐系统定位方法，可以实现相应的目标定位，如图15所示，其中发射船和接收阵的相对坐标由GPS记录数据计算。图15中叉状标识为GPS记录的目标实际位置，空心圆标识为经过直达波抑制后的时频分析定位结果，作为对比，星形标识为匹配滤波方法定位结果。

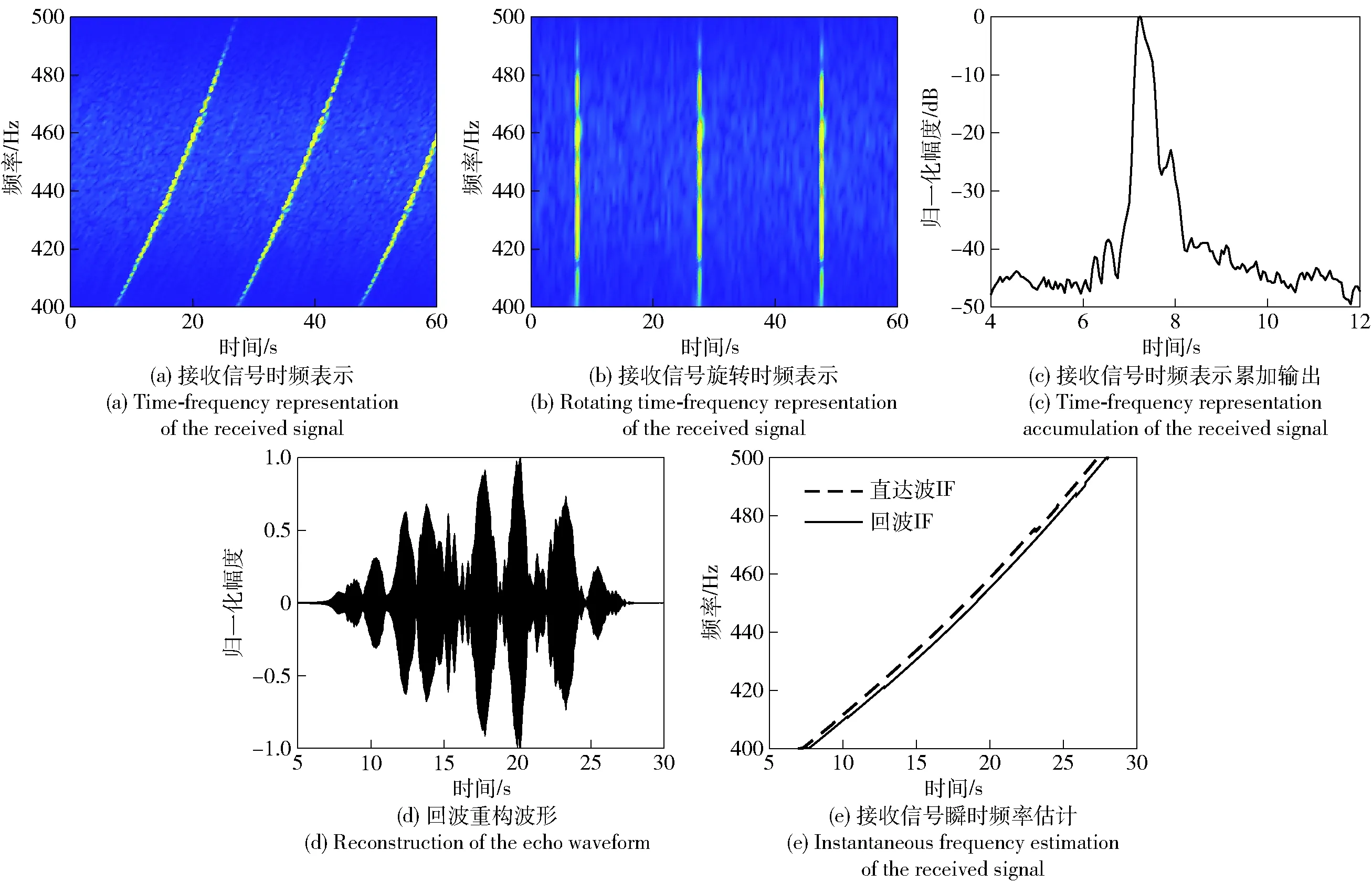
图13 实验信号参数化时频分析处理过程Fig.13 Parameterized time-frequency analysis and processing of the experimental signal

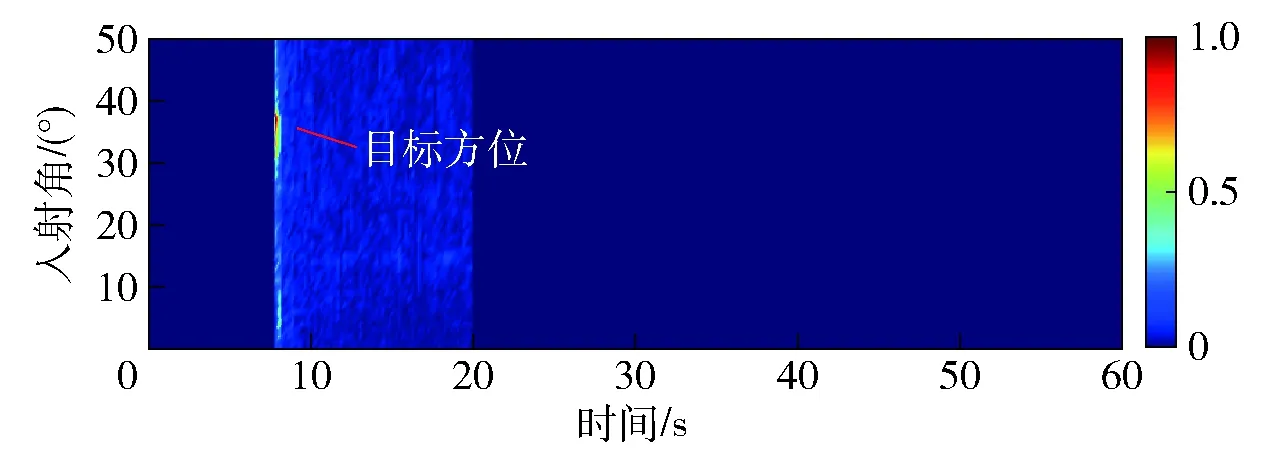
图14 直达波抑制后参数化时频变换方位- 时间序列输出Fig.14 Output of parameterized time-frequency transform azimuth-time series after direct wave suppression

图15 实验信号定位结果Fig.15 Experimental signal location

对站位1内四组实验接收信号分别进行参数化时频分析处理，比较处理前后的信噪比增益与定位误差，结果如表1所示。其中接收信噪比为经过阵列波束形成后得到的回波信噪比，输出信噪比为波束输出经过参数化时频变换后的回波峰值信噪比，理论增益值仍可由(21)式计算得出，均为29.0 dB；GPTF定位误差为参数化时频分析算法定位结果相对实际位置的均方误差。从表中可以看出，由于目标船体的姿态变化，同一站位内各段信号的接收信噪比有所起伏，但经过时频变换后获取的信噪比增益均接近理论值。作为对比，表1给出了相同站点匹配滤波结果的定位均方误差，如表1中MF定位误差所示。结合图12与图14可以看出，由于脉冲压缩的旁瓣较参数化时频变换更宽，且直达波干扰没有被抑制，直达波旁瓣导致的掩蔽覆盖真实目标方位，难以分辨确切的回波峰值位置，虚警导致的定位误差较大。而信号经过参数化时频分析处理与直达波抑制后，直达波旁瓣导致的掩蔽干扰减少，虚警降低，因此定位结果更接近于实际位置。

表1 站位1实验信号处理结果

实验结果表明，一方面，参数化时频分析方法可以有效地检测HFM连续波信号，获取显著的时频处理增益，充分利用HFM连续波信号的多普勒不变性，简化定位过程；另一方面，参数化时频分析可以通过时频域内的滤波和重构，分离直达波与目标回波分量，达到抑制直达波干扰的目的，有效解决了多基地CAS中的直达波干扰问题。

4 结论

本文提出了一种基于参数化时频分析方法的CAS信号处理方法，并将其应用于HFM连续波信号的检测和定位。基于发射HFM信号参数设计的参数化时频变换能够生成高集中度的信号时频表示，从而获取显著的信噪比增益，相应提升检测性能。同时通过旋转时频域内的滤波过程，仍掩盖在直达波的旁瓣，从而有效抑制直达波干扰。仿真结果表明，参数化时频分析方法应用于CAS探测领域，有效提升了HFM信号检测性能，并可以准确估计回波的时频特征，性能上优于传统子带滤波方法。实验结果验证了算法的可行性和有效性，该算法尤其适用于低信噪比条件下HFM信号的检测和定位，以及强直达波干扰下的弱回波信号检测。

[1] SAUNDERS W K. Post-war developments in continuous-wave and frequency-modulated radar[J]. Ire Transactions on Aerospace & Navigational Electronics, 1961, ANE-8(1): 7-19.

[2] VOSSEN R, SPEK E, BEERENS S. Low frequency continuous active sonar[C]∥Proceedings of the European Conference on Undersea Defence Technology. London, UK: Nexus Media, Ltd., 2011:1-4.

[3] HICKMAN G, KROLIK J L. Non-recurrent wideband continuous active sonar[C]∥Proceedings of 2012 Oceans. VA, USA: IEEE, 2012: 1-6.

[4] 吴迪, 周泽民, 曾新吾. M-COSTAS 复合编码连续主动声呐信号研究[J]. 信号处理, 2016, 32(10): 1187-1193.

WU D, ZHOU Z M, ZENG X W. Study on M-COSTAS novel coded multi-modulation continuous active sonar signal[J]. Journal of Signal Processing, 2016, 32(10): 1187-1193. (in Chinese)

[5] GRIMMETT D, WAKAYAMA C. Multistatic tracking for continous active sonar using Doppler-bearing measurements[C]∥Proceedings of the 16th International Conference on Information Fusion. Istanbul, Turkey: IEEE, 2013: 258-265.

[6] HAGUE D A, BUCK J R. The generalized sinusoidal frequency modulated waveform for active sonar[J]. IEEE Journal of Oceans Engineering, 2016, 42(1):109-123.

[7] 庞博, 吴一飞, 刘本奇. 连续波声呐中的调频信号设计方法及性能分析[J]. 声学技术, 2017,36(4): 327-334.

PANG B, WU Y F, LIU B Q. The design and performance of the frequency modulated signal for continuous active sonar[J]. Technical Acoustics, 2017, 36(4): 327-334. (in Chinese)

[8] MURPHY S M, HINES P C. Sub-band processing of continuous active sonar signals in shallow water[C]∥Proceedings of Oceans 2015. Genova, Italy: IEEE, 2015: 1-4.

[9] 刘大利, 刘云涛, 蔡惠智. 水下连续波有源探测的回波检测算法[J]. 声学学报, 2014, 39(2): 163-169.

LIU D L, LIU Y T, CAI H Z. An echo detection algorithm for underwater continuous wave active detection[J]. Acta Acustica, 2014, 39(2):163-169. (in Chinese)

[10] 周泽民, 曾新吾, 关承宇,等. 连续波主动声呐的直达波抑制处理方法研究[J]. 应用声学, 2019, 38(4):674-680.

ZHOU Z M, ZENG X W, GUAN C Y, et al. Research on strong direct blast suppression for continuous active sonar[J]. Applied Acoustics, 2019, 38(4):674-680. (in Chinese)

[11] KWOK H K, JONES D L. Improved instantaneous frequency estimation using an adaptive short-time Fourier transform[J]. IEEE Transactions on Signal Processing, 2000, 48(10): 2964-2972.

[12] BELTRAN J R, LEON J P D. Estimation of the instantaneous amplitude and the instantaneous frequency of audio signals using complex wavelets[J]. Signal Processing, 2010, 90(12): 3093-3109.

[13] BARKAT B, BOASHASH B. Instantaneous frequency estimation of polynomial FM signals using the peak of the PWVD: Statistical performance in the presence of additive Gaussian noise[J]. IEEE Transactions on Signal Processing, 1999, 47(9): 2480-2490.

[14] YANG Y, PENG Z K, DONG X J, et al. General parameterized time-frequency transform[J]. IEEE Transactions on Signal Processing, 2014, 62(11): 2751-2764.

[15] 杨扬. 参数化时频分析理论, 方法及其在工程信号分析中的应用[D]. 上海: 上海交通大学, 2013.

YANG Y. Theory and method of parametric time frequency analysis and its application in engineering signal analysis[D]. Shanghai: Shanghai Jiao Tong University, 2013. (in Chinese)

[16] ZHOU P, PENG Z, CHEN S, et al. Non-stationary signal analysis based on general parameterized time-frequency transform and its application in the feature extraction of a rotary machine[J]. Frontiers of Mechanical Engineering, 2018, 13(2): 292-300.

[17] 王璐, 许录平, 张华, 等. 基于S变换的脉冲星辐射脉冲信号检测 [J]. 物理学报, 2013, 62(13): 596-605.

WANG L, XU L P, ZHANG H, et al. Detection of pulsar radiation pulse signal based on S-transform[J]. Acta Physica Sinica, 2013, 62(13): 596-605. (in Chinese)

[18] 顾怡鸣,李整林,宫在晓,等.浅海负跃层条件下的双基地有源探测实验及定位声速修正[J]. 声学学报, 2019, 44(4): 429-441.

GU Y M, LI Z L, GONG Z X, et al. Experimental verification of bistatic active detection and propagation speed correction in shallow water with negative thermocline[J]. Acta Acustica, 2019, 44(4): 429-441. (in Chinese)

[19] OLHEDE S, WALDEN A T. A generalized demodulation approach to time-frequency projections for multicomponent signals[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2005, 461(2059): 2159-2179.

[21] 刘大利. 连续波主动声呐探测性能分析[C]∥2018年全国声学大会论文集 C水声工程和水声信号处理. 北京: 中国声学学会, 2018: 2.

LIU D L. Detection performance analysis of continuous active sonar[C]∥Proceedings of the 2018 National Acoustic Conference C Underwater Acoustic Engineering and Underwater Acoustic Signal Processing, Beijing, China: ASC, 2018:2. (in Chinese)

[22] 曹伟浩,姚直象,夏文杰,等. 基于插值短时分数阶傅里叶变换- 变权拟合的线性调频信号参数估计[J].兵工学报, 2020, 41(1): 86-94.

CAO W H, YAO Z X, XIA W J, et al. Parameter estimation of linear frequency modulation signal based on interpolated short-time fractional fourier transform and variable weight least square fitting[J]. Acta Armamentarii, 2020, 41(1): 86-94. (in Chinese)

[23] 孙文俊, 杨益新. 基于蒙特卡洛方法的主动声纳信号检测性能分析[J]. 计算机仿真, 2006, 23(8): 119-121.

SUN W J, YANG Y X. Performance analysis of signal detection for active sonar based on Monte Carlo method[J]. Computer Simulation, 2006, 23(8): 119-121. (in Chinese)

[24] 于勇. 基于广义参数化时频变换的铁路信号目标自动检测方法[J].自动化与仪器仪表, 2021(5): 17-20,24.

YU Y. Automatic detection method of railway signal target based on generalized parametric time frequency transform[J]. Automation & Instrumentation, 2021(5): 17-20,24. (in Chinese)

[25] 薛永华,陈小龙,黄勇,等.基于广义参数化时频变换的天波雷达电离层污染校正[J].信号处理, 2020, 36(12): 2024-2031.

XUE Y H, CHEN X L, HUANG Y, et al. Ionospheric pollution correction for sky wave radar based on generalized parametric time frequency transform[J]. Journal of Signal Processing, 2020, 36(12): 2024-2031. (in Chinese)

[26] 张烈山,刘璞,林杰俊,等.基于重采样的主动非线性调频连续波声呐测距技术研究[J]. 仪器仪表学报, 2020, 41(10): 74-82.

ZHANG L S, LIU P, LIN J J, et al. Research on active nonlinear frequency modulation continuous wave sonar ranging technology based on re-sampling[J]. Chinese Journal of Scientific Instrument, 2020, 41(10): 74-82. (in Chinese)

[27] 庞玉红,严琪,王世闯.基于瞬时频率的双曲调频信号距离估计误差分析[J]. 声学技术, 2016, 35(5): 421-425.

PANG Y H, YAN Q, WANG S C. Instantaneous-frequency-based ranging bias analysis of HFM waveforms[J]. Technical Acoustics, 2016,35(5):421-425. (in Chinese)

[28] 张蒙,王海斌,张海如,等.基于粒子滤波的多普勒信息辅助目标定位跟踪算法[J]. 应用声学, 2021, 40(3): 407-414.

ZHANG M, WANG H B, ZHANG H R, et al. Doppler information-assisted target tracking algorithm based on particle filter[J]. Applied Acoustics, 2021, 40(3): 407-414. (in Chinese)

[29] WANG J, HAN Y, WANG L M, et al. Instantaneous frequency estimation for motion echo signal of projectile in bore based on polynomial chirplet transform[J]. Russian Journal of Nondestructive Testing, 2018, 54(1): 44-54.

[30] 王璐, 许录平, 张华. 利用S变换的X射线脉冲星信号恒虚警率检测算法[J]. 宇航学报,2014, 35(8): 931-937.

WANG L, XU L P, ZHANG H. CFAR detection algorithm of X-ray pulsar signal using S-transform[J]. Journal of Astronautics, 2014, 35(8): 931-937. (in Chinese)