基于超临界二氧化碳的导弹弹射装置内弹道建模与优化

赵子熹，姜毅，贾启明，李玉龙，牛钰森

(1.北京理工大学 宇航学院， 北京 100081； 2.火箭军研究院 系统工程研究所， 北京 100085)

0 引言

弹射技术在航空航天特别是导弹发射领域得到广泛应用。除电磁弹射外，其余导弹弹射方式均依赖工作介质做功，以满足设计的弹射指标要求。根据工作介质的类型，导弹弹射方式可分为火药燃气式、燃气- 蒸汽混合式、压缩气体式、液力式和超临界流体式等。

现阶段相对成熟的火药燃气式弹射装置存在热防护要求较高、发射时隐蔽性较差等缺点；压缩气体式弹射装置则在设备复杂度、弹射有效载荷等方面表现出一定的劣势。超临界流体特别是超临界二氧化碳一方面具有较高的工作压强，可适配较大区间的弹射载荷需求；另一方面工作温度相对较低，在弹射过程中对导弹的影响较小，同时还具有比内能相对较高、发射时光热信号强度低、清洁环保等优点，逐步进入研究者的视野。

对基于超临界流体的弹射装置进行研究，一个关键在于正确表征流体的热物性参数。超临界流体的压强一般较高，经典的理想气体假设已不再适用，可按照真实气体进行处理。Ren等基于改进的维里方程构建以高压空气为工质的弹射动力学方程，对比了基于真实和理想气体假设的仿真结果，得到了真实气体效应对弹射动力学特性有显著影响的结论。姚琳等基于Peng-Robinson方程构建了两级提拉式单侧弹射装置内弹道模型并通过缩比实验验证了仿真结果；在建模仿真的基础上以气源体积为优化目标建立优化模型，有效提升了发射装置机动性。Yao等对基于超临界二氧化碳的无人机弹射装置进行了研究，在构建气- 液两相弹射动力学方程的基础上探讨了高压室初始状态等参数对弹射过程的影响，发现与空气等传统工质相比，超临界二氧化碳作为一种新型工作介质具有较高的工作效能。

前述文献在建立动力学模型时，均采用具有高压室- 喷管/阀门- 低压室形式的弹射装置，在处理喷管流动时引入具有解析形式的流量表达式，并未讨论真实气体效应对喷管流动造成的影响。由于超临界流体流经喷管时仍具有较高压强，不能被简单视为理想气体，有必要作为真实气体处理。同时部分文献中的弹射内弹道优化模型主要采用的是单目标优化思想，难以从多个维度反映弹射装置效能。

本文针对使用超临界二氧化碳作为工质的导弹弹射装置，基于Soave-Redlich-Kwong(S-R-K)状态方程建立了弹射内弹道动力学模型，特别是考虑了工质经喷管由高压室向低压室流动过程的真实气体效应。在内弹道模型的基础上构建多目标优化模型，对内弹道参数进行了优化设计。计算和优化结果对超临界二氧化碳在弹射系统中的应用具有一定的参考意义。

1 基于超临界二氧化碳的弹射动力学模型

1.1 模型假设

导弹弹射装置采用垂直发射装置，主要由高压室、喷管和低压室三部分组成，结构如图1所示。在弹射过程开始前，超临界二氧化碳存储于高压室中，喷管处于关闭状态。弹射开始后，喷管打开，超临界二氧化碳进入低压室，推动导弹运动。

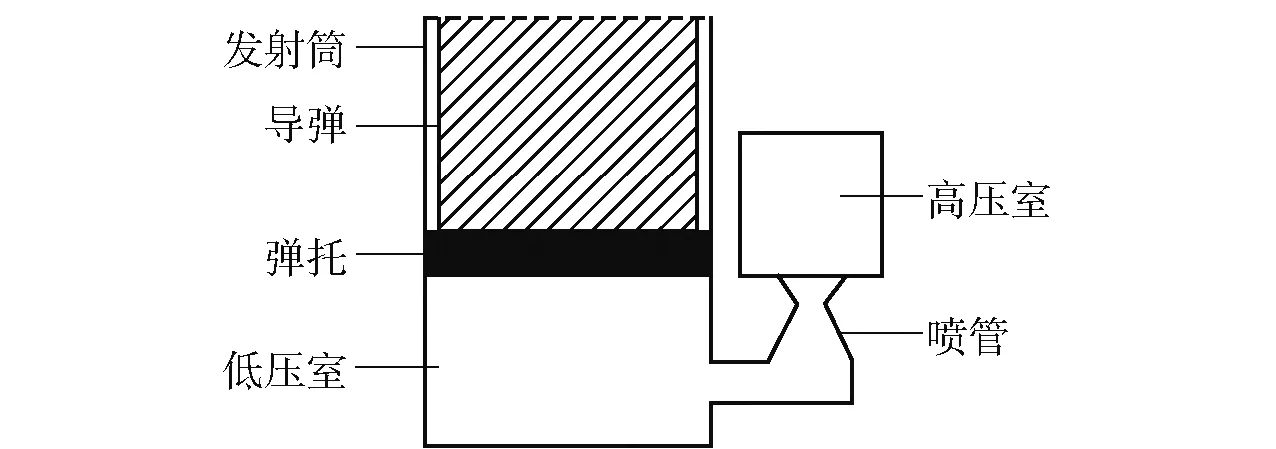
图1 弹射装置结构简图Fig.1 Schematic diagram of the catapult

在构建内弹道动力学模型前，给定如下基本假设：

1)弹射过程视为单相过程，即将弹射装置任一组成部分中的工质作为均一相处理，不考虑多相平衡共存的情况。

2)根据文献[5]的实验及数值仿真结果，喷管内超临界二氧化碳流动存在非平衡凝结等现象，增加了建模和计算的复杂性。为简化问题，引入准平衡思想，认为超临界二氧化碳在喷管中的流动由一系列平衡状态构成，忽略非平衡过程带来的影响。在假设1的基础上认为喷管内工质流动属于单相、平衡过程。

3)工质在喷管内流动视为一维等熵绝热流动，不考虑管内激波、摩擦等对流动造成的影响。

4)工质在喷管内流动始终作为临界流动处理，即喷管喉部流动马赫数始终为1。

5)除喷管外高压室和低压室内工质状态量在空间均匀分布，只随时间变化。

6)导弹在低压室的运动是无摩擦的，即忽略导弹适配器等因素的影响。

7)忽略系统与外界环境之间的能量交换。

1.2 真实气体状态方程

1.2.1 Soave-Redlich-Kwong状态方程

理论建模中一般通过状态方程引入真实气体效应。S-R-K状态方程是Soave基于Redlich-Kwong方程提出的一种立方型状态方程，以在多个应用领域中体现出的精度而著称。S-R-K方程可表示为

(1)

式中：为工质压强；为特定气体常数；为工质温度；为工质比体积；为物质偏心因子；、为特定物质常数，与特定物质的关系为

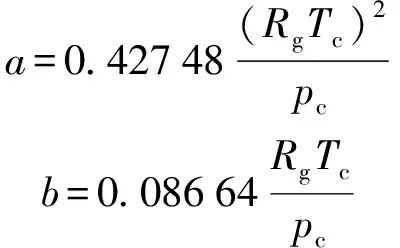
、分别为物质的临界温度和临界压强；(，)为与工质温度相关的修正函数，

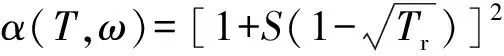
(2)

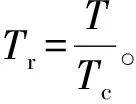
122 超临界二氧化碳热物性参数建模

基于选定的状态方程，构建超临界二氧化碳定压比热容、比焓等状态量计算表达式。计算公式为

(3)

式中：为工质定容比热容；、和间的偏导数可根据状态方程(1)式及偏导数关系得到

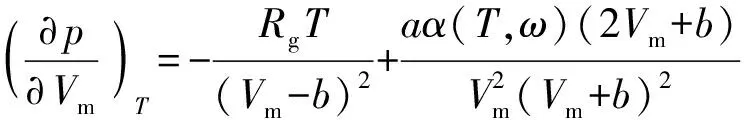
(4)

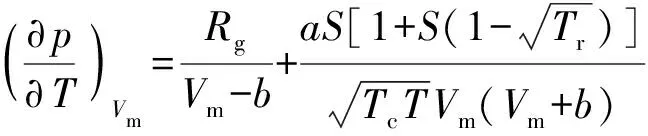
(5)

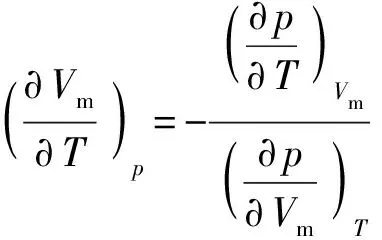
(6)

对于真实气体或超临界流体而言，不仅与温度有关，还受到压强的影响。根据Maxwell关系式及状态方程表达式，有

(7)

设想工质密度由0 kg/m变化至特定值的等温过程，则可表示为

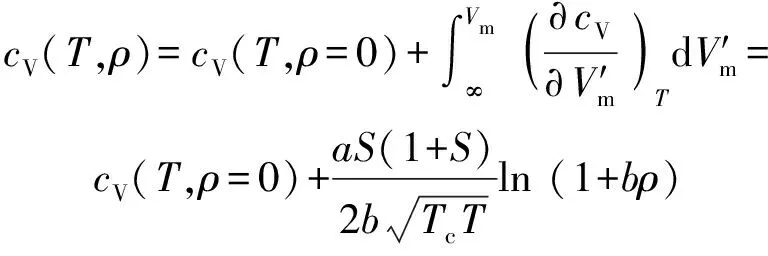
(8)

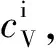
(9)

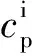
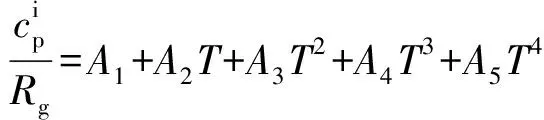
(10)

(=1,2，…，5)为系数，=2535 6，=8067 1×10，=-5706 1×10，=1793 9×10，=-1528 2×10。

(10)式的适用范围为100～1 477 K。将(4)式～(10)式代入(3)式，即可计算特定压强和温度下工质定压比热容。

比焓可表示为

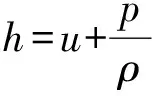
(11)

式中：为工质比内能，对于真实气体，为和的函数，

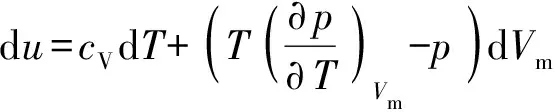
(12)

设想一个工质密度由0 kg/m变化至的等温过程，则的变化为

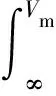
(13)

综合(9)式、(10)式、(12)式、(13)式及(4)式，可得的表达式为

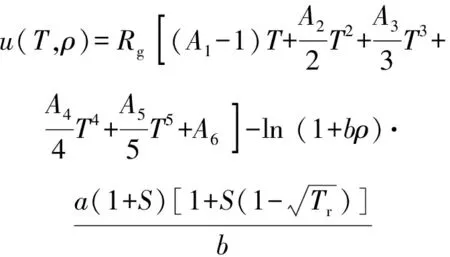
(14)

式中：为常数系数，=58817 9。结合(11)式、(14)式可得特定压力及温度下的工质比焓计算式。

根据相同建模思想可获得工质比熵的计算式为

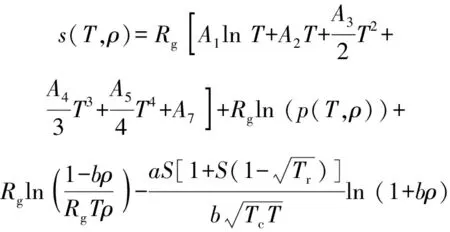
(15)

式中：为常数系数，=9895×10。

123 S-R-K状态方程验证

为确认S-R-K状态方程的精度，将基于该状态方程计算的二氧化碳压强、定压比热容、比焓和比熵等状态量与美国国家标准与技术研究院(NIST)数据库中的相关数据进行对比，结果如图2所示。使用的二氧化碳物性参数如表1所示。

表1 二氧化碳热物性参数

以NIST为基准时计算值平均相对误差如表2所示。

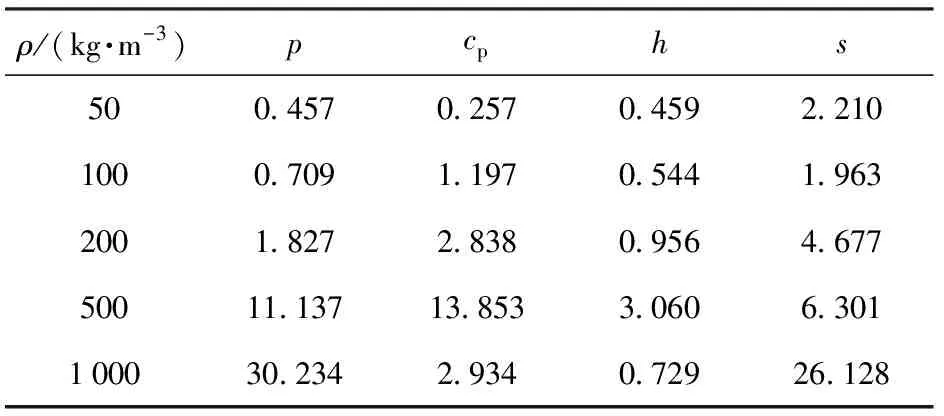
表2 热物性参数平均相对误差

根据图2及表2，在给定的温度范围内当二氧化碳密度小于500 kg/m时，基于S-R-K方程计算的压强、定压比热容、比焓和比熵等物理量与NIST数据较为一致，平均相对误差均维持在5%以内。随着密度增大，压强和比熵计算误差逐渐增大，接近或超过30%，表明S-R-K方程预测二氧化碳热物性参数的能力有所减弱；定压比热容的计算误差增加至约15%后减小，同时热物性参数模型也相对准确地预测了临界点附近的参数跃变；比焓计算值的偏差始终较小，平均相对误差始终保持在4%以内。

图2 基于S-R-K方程的二氧化碳热物性参数计算值与NIST数据对比Fig.2 Comparison of the thermal physical results of carbon dioxide calculated by S-R-K equation with NIST data

综合上述分析，认为当密度处于一定范围内(≤500 kg/m)时，S-R-K状态方程预测的二氧化碳物性参数计算误差相对较小，可以满足后续内弹道计算需求。

1.3 考虑真实气体效应的一维等熵喷管流动模型

1.3.1 一维等熵喷管流动模型

喷管作为连通高、低压室的部件，其流动特性直接决定低压室工质状态，进而影响弹射效能。根据能量守恒原理，一维喷管流动的能量方程为

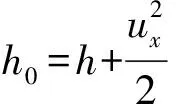
(16)

式中：为滞止状态比焓；为喷管中距入口距离处的工质流动速度。以下标t表示喷管喉部，则喷管流量可表示为

(17)

式中：为喷管喉部横截面积；为滞止状态压力；为滞止状态密度；为无量纲流动系数，

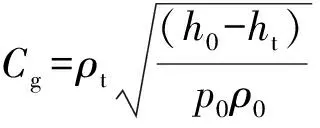
(18)

为喷管喉部密度，为喷管喉部的比焓。根据(17)式、(18)式即可确定喷管临界流量。

132 一维等熵喷管流动的迭代解法

根据熵的定义式和Maxwell关系式，熵可表示为

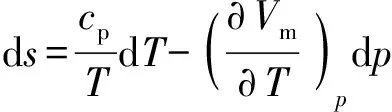
(19)

基于等熵流动假设d=0，可得

(20)

真实气体比焓可表示为温度和压强的函数：

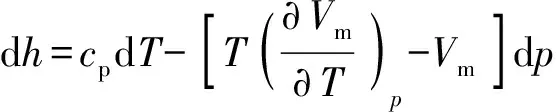
(21)

将(20)式、(21)式改写为如下迭代形式：

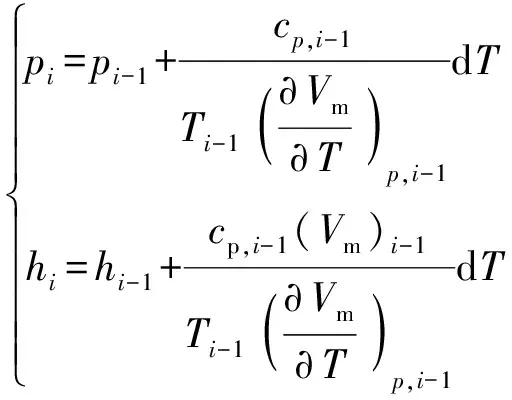
(22)

式中：下标表示第个网格节点。根据喷管流动的定性分析，临界流动下温度沿流向降低，即d始终为负值。因此可以沿轴向将喷管空间离散为若干网格节点，给定计算步长d，则温度的迭代计算式为

=-1+d

(23)

迭代计算需要设置计算终止条件。弹射内弹道问题对于喷管部分，主要关注喷管流量。根据临界流动假设，流动达到临界状态后，流量不再随喷管出入口压力比的减小而增加。临界流量在工程实践中常用喉部流量表示。同时喷管内马赫数沿流向增加，在喉部始终为1。综上，迭代终止准则可设置为：当网格点处马赫数≥1时停止计算，最接近1的马赫数对应的网格节点可以表示喷管喉部。在确定喉部位置的基础上，根据(17)式、(18)式计算的流量值即为喷管临界流量。为计算马赫数，首先根据声速定义有

(24)

式中：表示声速。等熵条件下压强对比体积的偏导数根据状态方程推导为

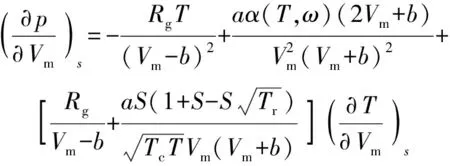
(25)

对于右端新增的等熵条件下温度对比体积的偏导数，注意到熵还可表示为温度和比体积的函数：

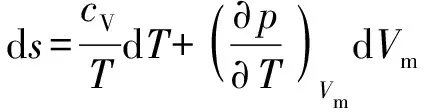
(26)

由等熵假设可得：

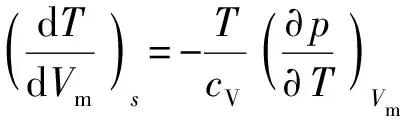
(27)

综合(4)式、(25)式、(27)式并将其代入(24)式即得声速计算式。在解出声速的基础上即可确定对应网格点处马赫数。

以上给出了一维等熵喷管流动迭代解法的基本思想。实际计算时，首先确定计算步长d，之后根据(22)式、(23)式进行迭代求解。求得网格点处温度、压强和比焓后，密度由状态方程(1)式确定，速度由能量方程(16)式确定。

133 喷管流动模型验证

在构建喷管流动模型的基础上进行网格无关性验证，网格步长d取值范围为-005～-0002 K。初始条件设置如表3所示，喷管喉部直径为85 mm。

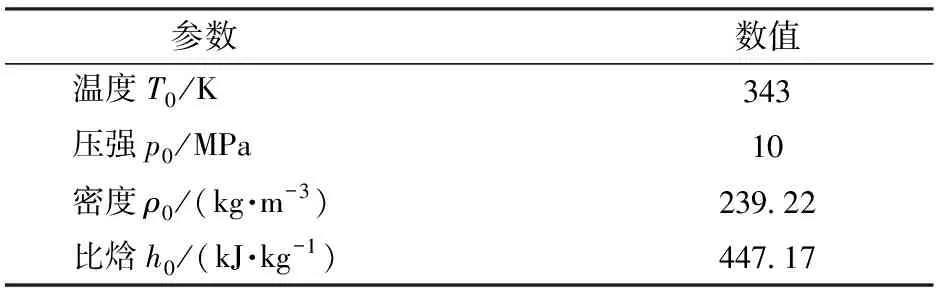
表3 网格无关性验证初始条件

网格无关性验证结果如图3所示。

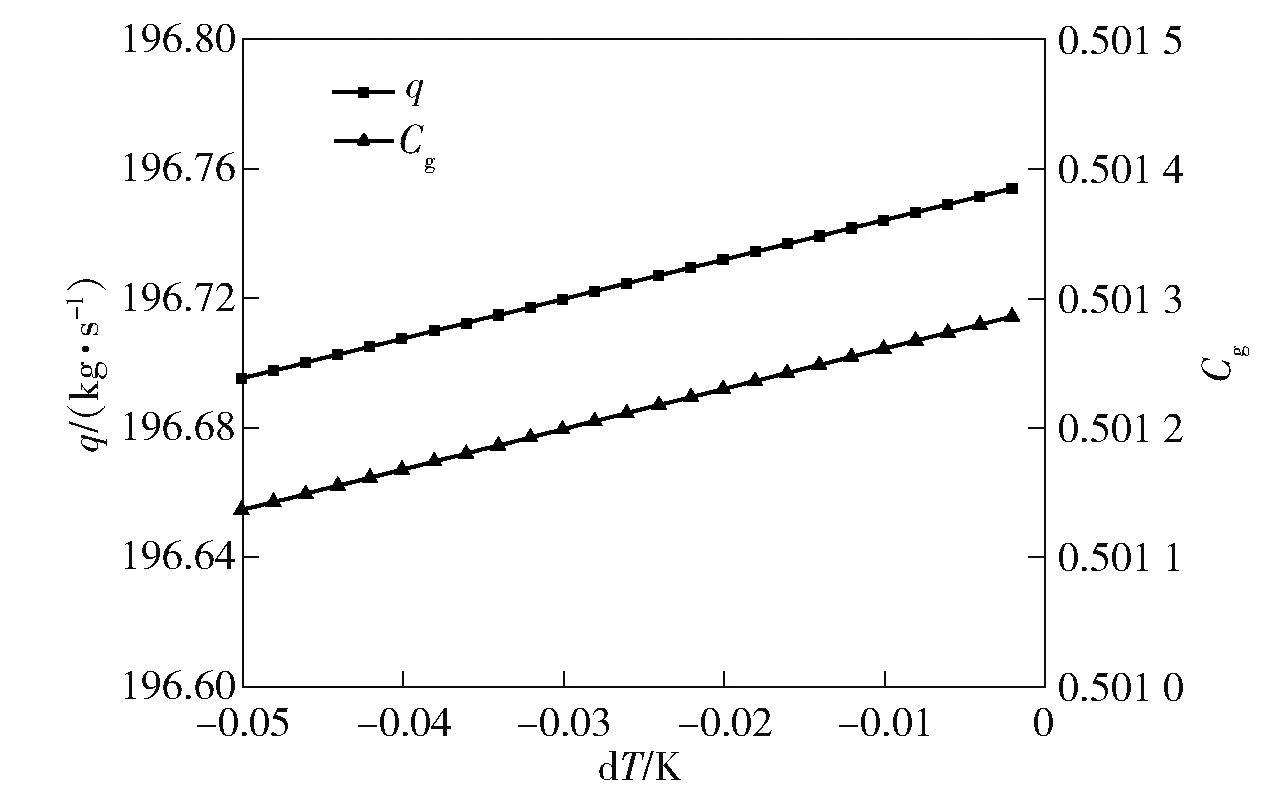
图3 喷管流动模型网格无关性验证Fig.3 Grid independence validation of the nozzle flow model

根据图3可知，随着计算步长绝对值的减小，流量和无量纲流动系数均呈现增长趋势。若以计算步长-0.05 K作为对照基准，则流量最大绝对差值为0.059 kg/s，对应相对差值为0.029 8%；无量纲流动系数最大绝对差值为0.000 15，对应相对差值为0.029 9%。验证计算表明，计算步长对喷管流动流动模型计算结果影响较小，后续计算时可在综合计算时间成本等因素基础上在-0.03～-0.01 K的范围内设置步长。

流量作为喷管流动的关键参数之一，可在一定程度上衡量模型与实际的近似程度。为此将流量值与相关文献实验数据进行对比。网格步长设定为-0.025 K，喷管喉部直径为1.014 mm，其余初始条件设置如表4所示。

表4 流量验证计算初始条件

流量计算值与实验值对比如图4所示。

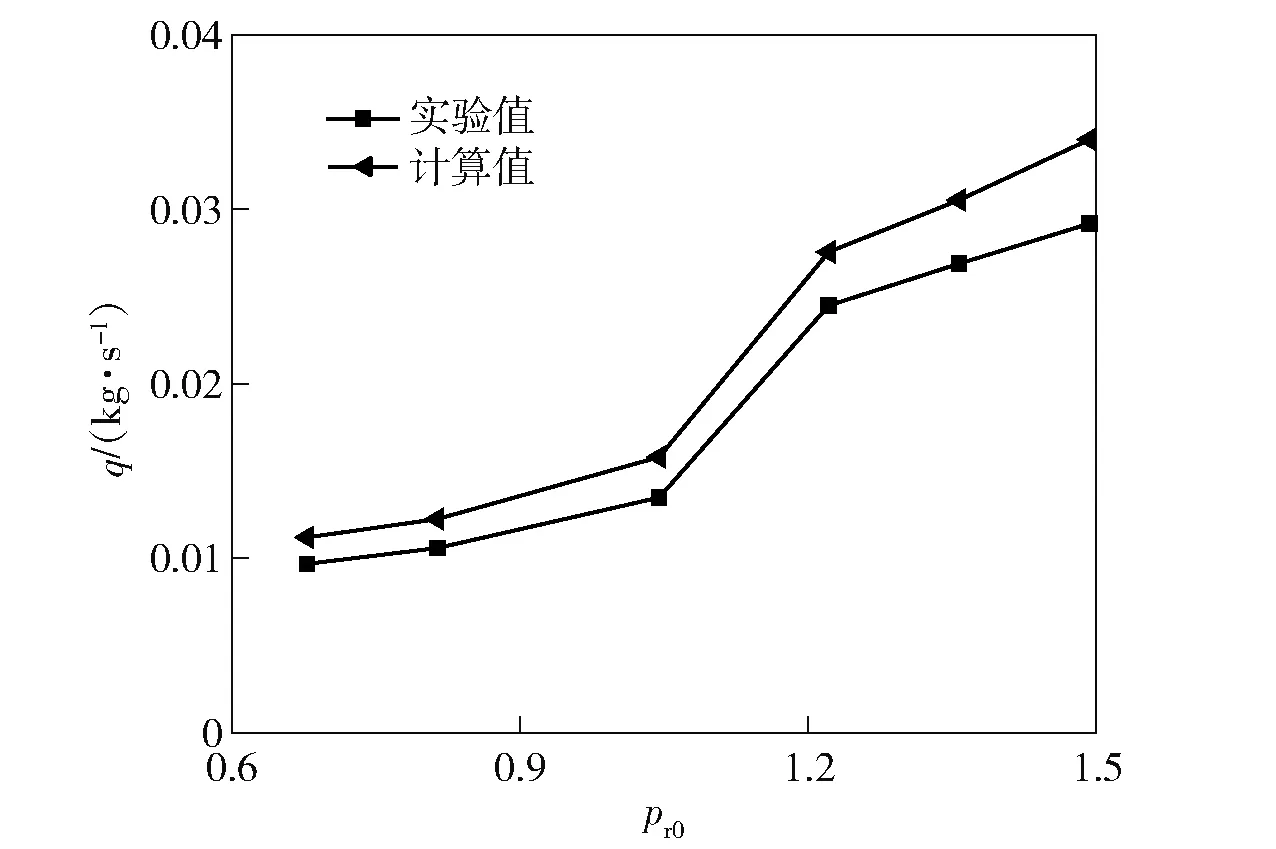
图4 喷管流动模型流量验证Fig.4 Mass flow verification of the nozzle flow model

图4中横坐标为喷管滞止状态下对比压强：

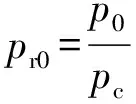
以实验数据作为基准，流量计算值误差如表5所示。

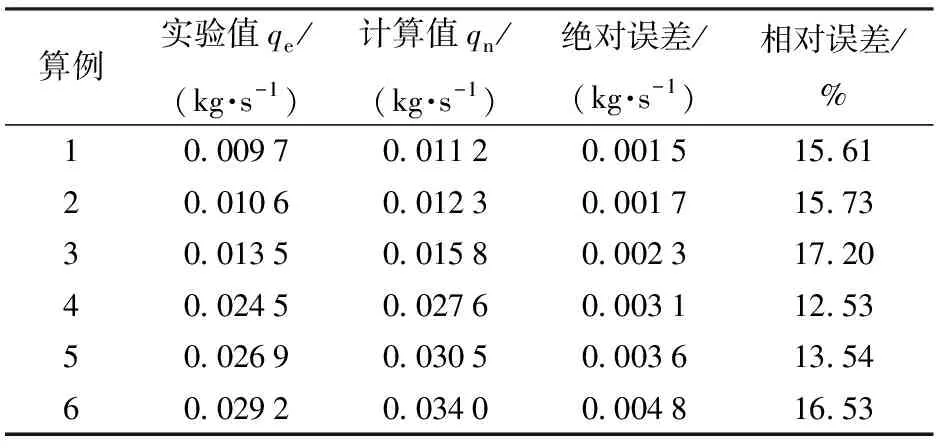
表5 流量计算误差

根据图4及表5可知：计算绝对误差随对比压强增加而增加；相对误差呈波动趋势，始终保持在10%～20%的范围内。在实验本身也可能存在测量仪器等多个误差来源的前提下认为计算误差在可接受范围内。沿流动方向的比熵随马赫数变化如图5所示。

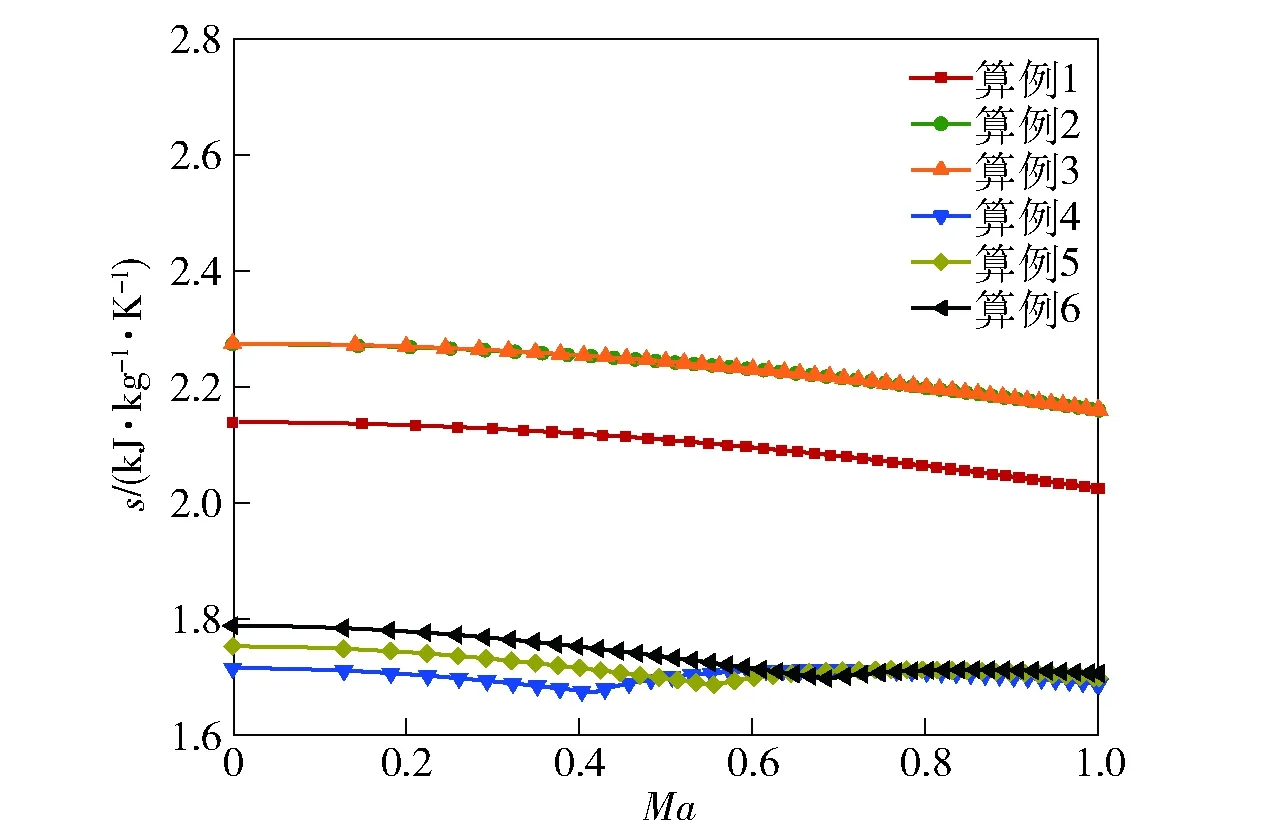
图5 沿流动方向比熵变化Fig.5 Specific entropy variation along the flow direction

由于本文关注的重点是喷管的临界流量，比熵变化只考虑了由滞止状态加速至声速的流动。根据图5可知，在不同滞止状态下随着二氧化碳加速流动，沿流向熵值呈现一定波动，但相对于滞止状态的最大变化量保持在5%以内。因此认为等熵假设可以满足工程计算需求，喷管流动模型可行性和合理性得到验证。

1.4 弹射内弹道动力学模型

1.4.1 内弹道模型

以下标1表示高压室，基于质量守恒原理、能量守恒原理、真实气体状态方程和比焓定义式建立的高压室动力学模型为

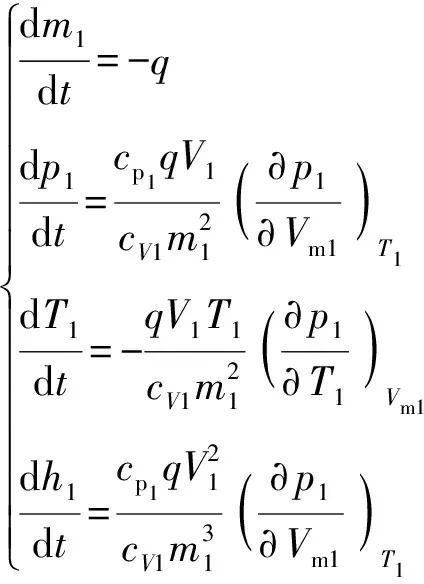
(28)

式中：为弹射初始时刻高压室中工质质量；为高压室压强；为高压室工质定压比热容；为高压室工质定容比热容；为高压室体积；为高压室工质比体积；为高压室温度；为高压室工质比焓。

以下标m表示包含弹托的导弹，下标2表示低压室，基于导弹运动学和动力学关系、质量守恒原理、能量守恒原理、真实气体状态方程和比焓定义式建立的低压室动力学模型为

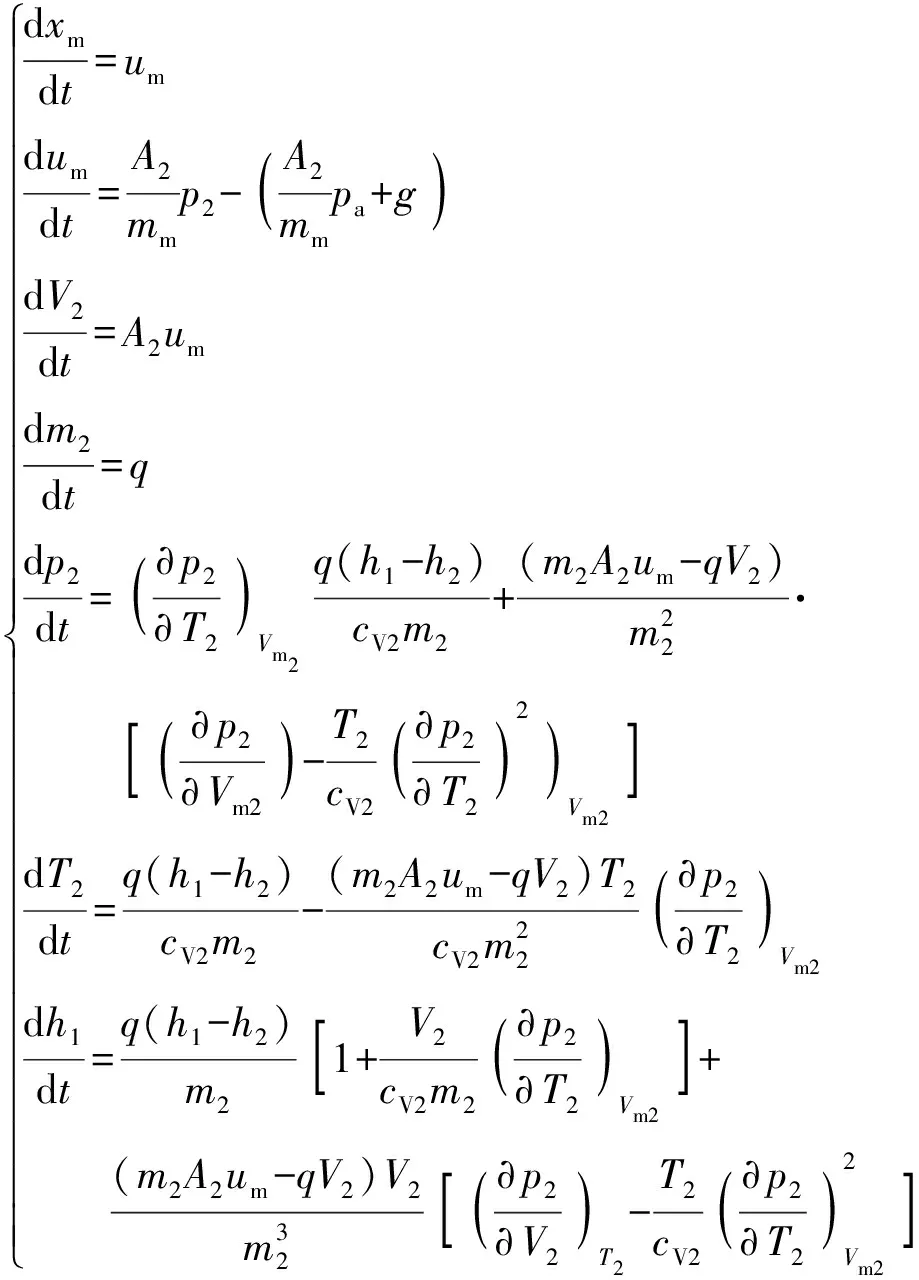
(29)

式中：、分别为导弹位移和速度；为导弹质量；为低压室有效推力面积；为低压室压强；为大气压；为重力加速度；为低压室体积；为低压室工质质量；为低压室温度；为低压室工质比体积；为低压室工质定容比热容；为低压室工质比焓。

142 内弹道模型验证

将基于超临界空气的垂直发射装置内弹道计算结果与文献数据进行了对比，干空气热物性参数如表6所示。

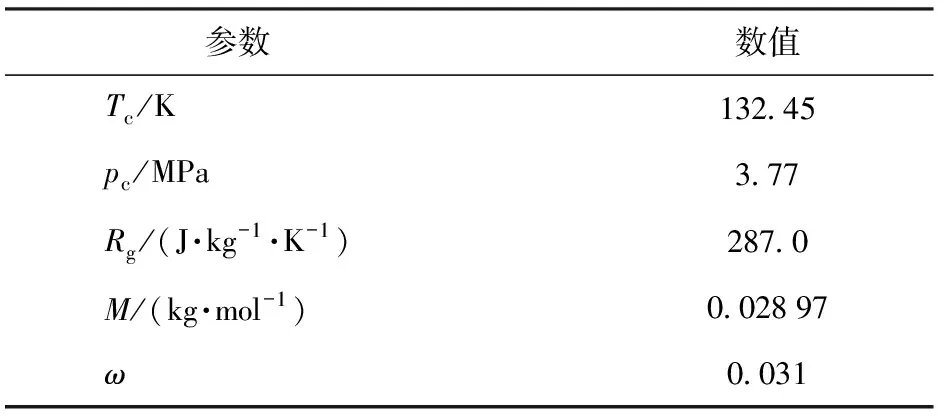
表6 干空气热物性参数

用于内弹道模型验证的仿真参数如表7所示。

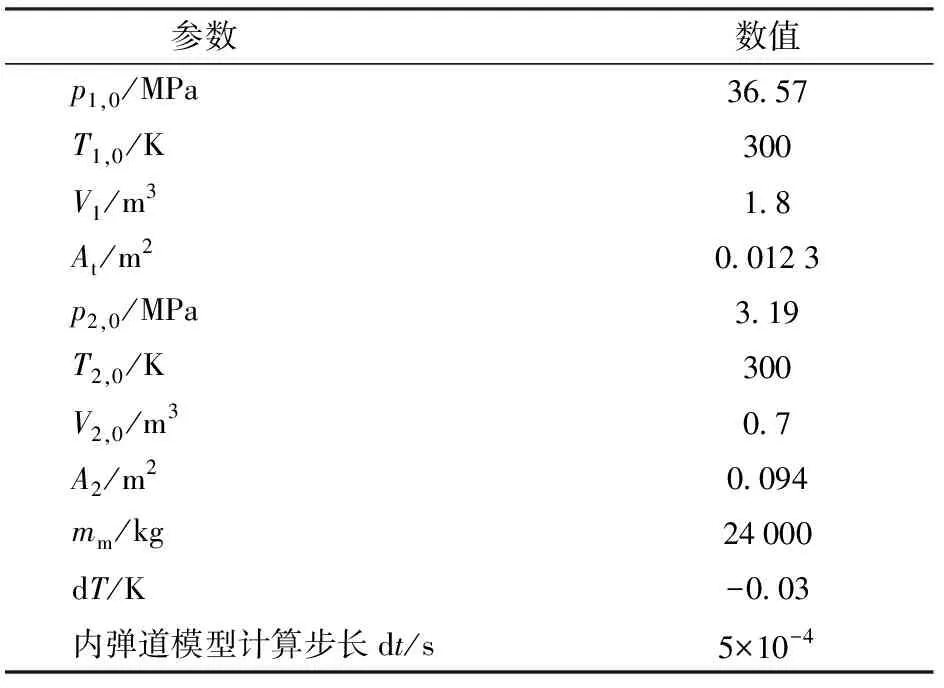
表7 内弹道模型验证仿真参数

内弹道模型验证结果如图6所示。

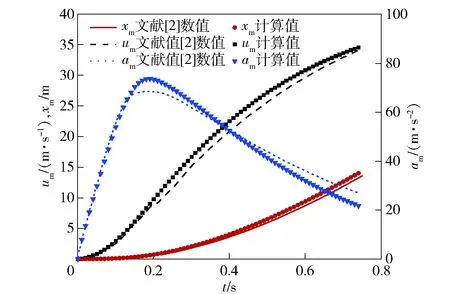
图6 基于空气的内弹道计算结果与文献[2]数据对比Fig.6 Comparison of the calculated interior ballistics results based on air with the data from Ref.[2]

根据图6，基于前文内弹道模型计算的导弹加速度、速度、位移等参数与文献[2]数据相比，吻合较好。计算值与文献[2]数值的变化趋势一致，具体数值存在一定差别。以文献[2]数值作为基准，则计算的加速度最大绝对差值为5.178 m/s，对应的相对差值为7.56%；速度最大绝对差值1.622 m/s，对应的相对差值为13.74%；位移最大绝对差值0.672 m，对应的相对差值为5.47%。

综合上述分析可知，考虑到文献[2]中使用的建模方法与本文有所区别，认为计算结果差值在可接受范围之内，本文使用的内弹道模型合理性和可行性得到验证。

2 内弹道动力学仿真与优化

2.1 内弹道仿真计算

2.1.1 时间步长对计算影响

为研究时间步长d对内弹道模型仿真结果的影响，工质选定为超临界二氧化碳，在2×10～1×10s的范围内，以2×10s为间隔设计5个计算工况。设置喷管计算步长为-0.037 K，喷管喉部直径在0～0.4 s为85 mm，在0.4～0.6 s为120.2 mm，0.6 s之后为147.2 mm。计算初始条件及导弹参数如表8所示，取9.81 m/s。

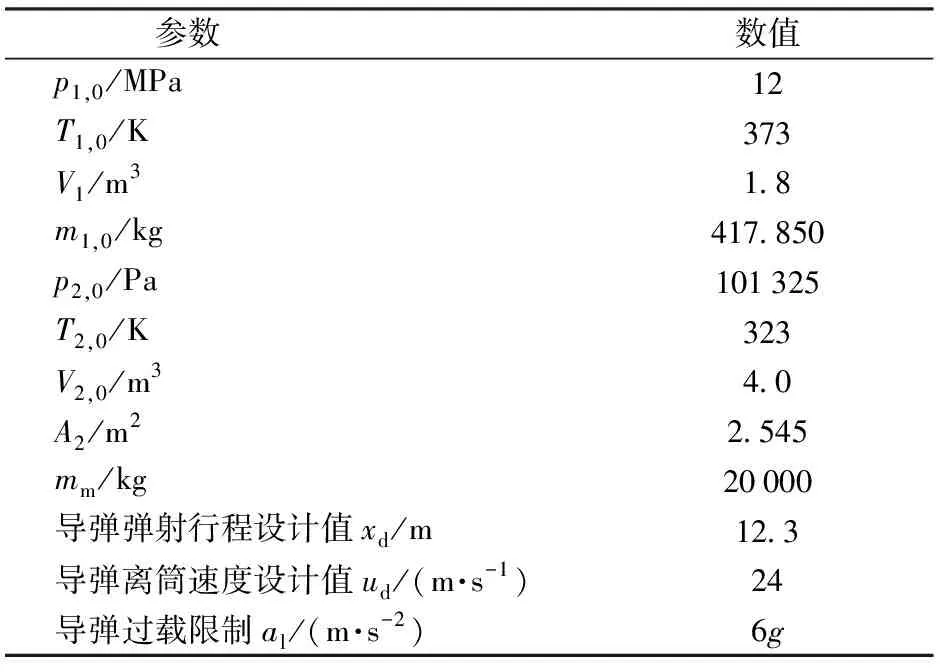
表8 时间步长对比计算参数

基于超临界二氧化碳的内弹道计算结果如图7所示。

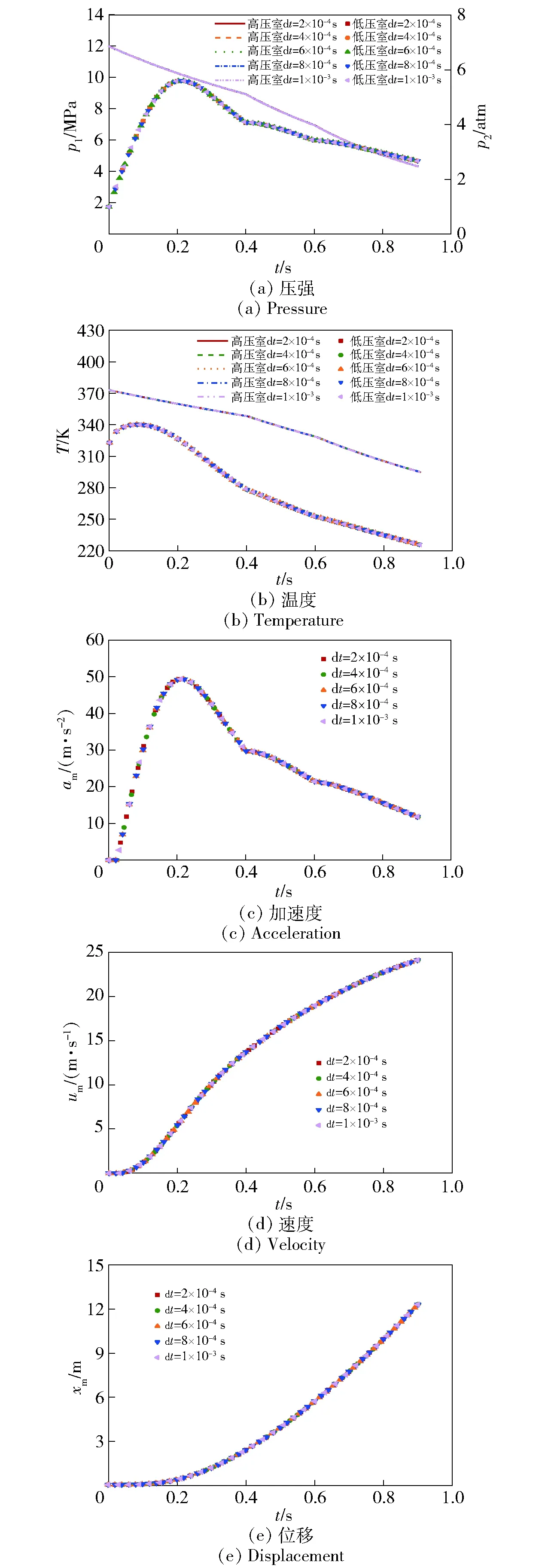
图7 不同时间步长计算结果对比Fig.7 Calculation results using different time steps

根据图7(a)可知，弹射开始后高压室压强由于工质流出而持续降低，低压室压强先升高后降低，峰值压强约为0.568 MPa。喷管喉部直径的变化有效减缓了低压室压强的下降。结合加速度变化曲线可知，改变喷管喉部横截面积可实现对弹射过程的控制。根据图7(b)，高压室温度由初始373 K降至约295 K，低压室温度先增大至约340 K后持续降至约225 K。由(29)式可知，在0.08 s之前高压室与低压室比焓差值相对较小，低压室温度对时间的导数为正值，使得低压室温度升高。根据图7(c)，导弹加速度峰值约5.05，未超过过载限制。根据图7(d)和图7(e)，导弹速度和位移随时间变化持续增加直至弹射过程终止。终止时刻的导弹运动学参数如表9所示。

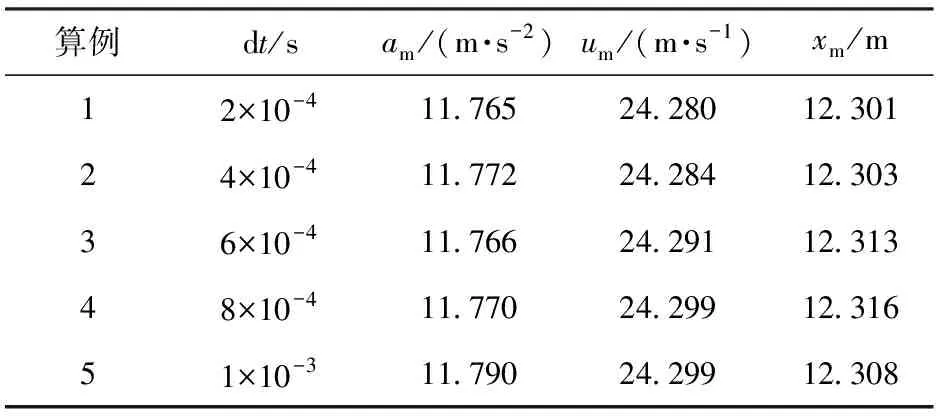
表9 弹射终止时刻导弹运动学参数

结合图7及表9可知，不同算例对应的高、低压室状态量及导弹运动学参数基本一致，表明内弹道模型对计算步长的变化不敏感，后续可在综合考虑求解精度及时间的基础上设置计算步长。

2.1.2 真实气体效应对计算影响

为研究真实气体效应对模型影响，对比了分别采用真实气体和理想气体模型的内弹道计算结果。仿真参数及内弹道方程组初始条件与2.1.1节中设置基本一致，计算步长取5×10s。计算结果如图8所示。

图8 理想气体和真实气体模型计算结果对比Fig.8 Comparison of calculation results for ideal gas and real gas models

由图8(a)可知，高压室压强持续降低；低压室压强在弹射初期上升，之后由于工质流入的增压效应无法抵消体积增大的影响而开始降低。基于理想气体模型计算的低压室压强峰值约0.626 MPa，明显大于真实气体模型计算结果0.568 MPa，相对差值约10.35%。根据(29)式即低压室内弹道方程组分析原因，高、低压室比焓差值(-)一项对低压室压强、温度和比焓变化率均具有重要影响。根据理想气体假设，工质比焓随温度增加而增加。在弹射初期，高压室温度高于低压室，导致由理想模型计算的高压室比焓显著大于低压室比焓。较大的比焓差值使得低压室压强峰值有较大幅度增加。

由图8(b)可知，弹射初始阶段高压室、低压室间较大的比焓差值也使得基于理想气体模型计算的低压室温度峰值与真实气体模型计算结果相比，增加约100 K左右。同时，综合图8(a)和图8(b)可知，真实气体效应对高压室压强、温度影响不明显。

由图8(c)可知，真实气体模型流量计算值大于理想气体计算结果，表明真实气体效应对喷管内工质流动存在影响。分析原因，主要是在相同的滞止压强和温度下，基于理想气体模型计算的工质密度显著低于真实气体模型计算值，同时不同模型计算的无量纲流动系数也存在差别。

由图8(d)可知，根据理想气体假设计算的导弹加速度在0～0.4 s之间明显偏大，峰值加速度为56.978 m/s。根据真实气体模型计算的峰值加速度为49.505 m/s，区别主要是由于理想气体模型计算的较高低压室压强造成的。加速度对比也表明理想气体模型下导弹运动存在超过过载限制的可能。弹射后期理想气体模型加速度下降速率与真实气体模型相比，有较小幅度增加。

综上所述，工质的真实气体效应对内弹道模型特别是低压室部分影响较大，建模和计算需要充分考虑相关因素。

2.2 内弹道优化设计

2.2.1 内弹道优化模型

为提升弹射整体效能，在仿真基础上设计了内弹道优化模型。由于单一评价指标无法充分体现不同优化方案的差别，引入多目标优化思想。

2.2.1.1 优化目标设定

优化目标一般要结合问题的具体背景确定。对于弹射过程，首要关注点在于能否实现给定的弹射指标即出筒速度。但由于并未严格限定出筒速度和设计值之间的偏差，出筒速度可以作为约束条件而非优化目标引入优化模型中。在此基础上弹射装置的整体效能，亦即为了实现预期目标所使用的工质和工质能量转化率成为关注重点。根据这一思想设计如下优化目标：

1)基于工质质量的目标函数。弹射装置使用的超临界二氧化碳质量一方面影响整体使用成本，另一方面决定了弹射装置体积。较大的体积将显著增加武器系统成本和受攻击风险。所需工质质量应当在满足弹射指标的情况下尽可能较少，同时为了使各目标函数的数量级保持一致，与工质质量相关的优化目标可表示为

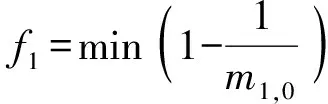
(30)

2)基于能量利用率的目标函数。工质的能量利用效率可用于评估弹射装置效能。给定工质能量利用率为

式中：为导弹离筒时刻机械能；u为初始时刻高压室内工质内能。总的能量利用率应当保持在相对较高的水平：

=min(1-)

(31)

2212 设计变量选取

设计变量的选取参考相关文献工作。高压室和低压室初始状态直接决定了弹射动力学特性，影响弹射效能。例如高压室初始压强、温度和体积共同决定了使用工质质量；低压室初始体积影响低压室内压强变化。因此选定高压室初始压强、高压室初始温度、高压室体积、低压室初始体积等4个变量作为设计变量。约束条件如下：

1)设计变量上下限约束。设计变量的取值范围应当结合问题物理背景进行限制：

(32)

式中：、上下限主要根据S-R-K方程精度设置；、上下限根据文献[1]的结论和试算确定。

2)喷管临界流动约束。根据内弹道模型假设，喷管流动始终处于临界状态。要求喷管出口和入口、即低压室和高压室压强之比不得大于临界值：

(33)

式中：为临界对比压比，等于喷管喉部压强与喷管入口处滞止压强之比。实际计算时该临界值由基于真实气体效应的一维等熵喷管流动模型确定。

3)低压室工质三相点约束。在弹射过程中，低压室工质温度存在下降阶段，可能降至工质三相点温度以下。此时若工质压强大于三相点压强，则相态为固态，可能造成弹射失败。该约束可表示为

<,<

(34)

式中：、分别为工质三相点的压强、温度。

4)导弹最大过载约束。弹射过程中由于弹体结构和弹上设备的要求，导弹加速度不得超过许用值：

≤

(35)

5)导弹出筒速度约束。导弹出筒速度应大于等于设计值：

≥

(36)

(30)式～(36)式即为内弹道优化模型。

2.2.2 基于多目标遗传算法的优化模型求解

基于多目标遗传算法——带精英策略的非支配排序的遗传算法对模型进行求解。仿真参数和弹射设计指标主要根据表8参数设置，内弹道模型计算步长为1×10s，低压室初始时刻温度为283 K。为了提高导弹出筒时刻机动性，出筒速度设计值调整为30 m/s。遗传算法相关参数设置为：种群数量50，迭代次数最大取120，交叉概率0.8。

随着迭代次数增加，Pareto最优解集对应的目标函数值变化如图9所示。

图9 Pareto最优解集对应目标函数变化Fig.9 Changes in the objective function corresponding to the Pareto optimal set

根据图9(a)可知，单个目标函数的最小值均随迭代次数增加而呈现下降趋势。相对迭代次数为60时，迭代次数120的情况下目标函数下降0.000 1%，目标函数下降0.001 9%，表明优化目标对迭代次数的变化更为敏感。根据图9(b)，随迭代次数增加，目标函数Pareto前沿在目标空间内沿函数值减小方向的推进比较明显，表明优化取得一定效果。同时由于优化目标的改进量相对较小，认为在现有条件下迭代次数设置在120的范围内是较为合理的。

120次迭代的Pareto解及对应目标函数值与特定基准工况对比如表10所示。

表10 迭代120次条件下优化结果对比

根据表10可知：与优化前相比，优化后的高压室压强增大21.09%，温度近似相等；高压室体积减小46.33%，低压室初始体积增加约44.67%。由于并未严格限定弹射装置整体的结构尺寸和安全性指标，其在当前问题中均属于次要因素，因此认为优化解相对合理。

目标函数方面，基础解所需的工质质量约为1 226 kg，优化后所需的工质质量减小至约831 kg，与基础解相比减少32.22%。能量利用率由2.10%增加至3.14%，增加49.52%。优化前后导弹运动参数曲线如图10所示。

图10 优化前后导弹运动学参数对比Fig.10 Comparison of missile kinematic parameters before and after optimization

根据图10可知，基准解所需弹射时间约0.965 s，优化后弹射时间增加至约1.011 s，相对优化前增加约4.76%。综合实际弹射过程认为，弹射时间增加所造成的影响可以近似忽略。优化后导弹加速度曲线在上升阶段更为平缓，加速度峰值到达时间延后。优化后加速度峰值约43.892 m/s，与优化前峰值43.443 m/s相比近似相等。优化后加速度曲线的相对平缓使得出筒时间有所延长，但如前所述对系统反应能力的影响可忽略不计。

3 结论

本文针对使用超临界二氧化碳作为工作介质的导弹弹射装置，基于S-R-K状态方程构建了内弹道动力学模型。在研究时间步长和真实气体效应对模型仿真结果影响的基础上，设计了多目标优化模型并进行求解。得到如下主要结论：

1)内弹道模型精度通过实验数据和相关文献仿真结果得到验证，表明本文建立的内弹道模型较为合理，模型采用的数值求解方法是有效的。

2)时间步长对计算结果影响不明显，表明可在综合精度和时间成本等因素的基础上选择合适的时间步长进行求解。

3)对比了采用理想气体模型和真实气体模型的计算结果，理想气体假设下低压室温度和压强在弹射过程中明显偏高，表明真实气体效应对计算存在比较显著的影响。

4)基于遗传算法的优化结果与参考值相比明显改进，工质用量减少32.22%，能量利用率提升49.52%。表明遗传算法对基于超临界二氧化碳的弹射器内弹道多目标优化问题具有一定适用性，优化后的弹射系统多项指标均有改进。

后续可在引入多相共存及非平衡效应的基础上建立更为精细的内弹道模型，使计算结果更加准确。

[1] 谭大成.弹射内弹道学[M].北京:北京理工大学出版社，2015.

TAN D C.Interior ballistics of catapult[M].Beijing:Beijing Institute of Technology Press，2015.(in Chinese)

[2] REN J，YANG F B，MA D W，et al.Pneumatic performance study of a high pressure ejection device based on real specific energy and specific enthalpy[J].Entropy，2014，16(9):4801-4817.

[3] 姚琳，马大为，马吴宁，等.两级提拉式单侧弹射装置内弹道建模与优化[J].兵工学报，2017，38(3):466-475.

YAO L，MA D W，MA W N，et al.Interior ballistics modeling and optimization of one-side ejection device with two-step cylinder[J].Acta Armamentarii，2017，38(3):466-475. (in Chinese)

[4] YAO H X，WEI X Y，YE H. Supercritical carbon dioxide as a new working medium for pneumatic launch: a theoretical study[J]. Defence Technology，2020，17(4):1296-1306.

[5] LETTIERI C，PAXSON D，SPAKOVSZKY Z，et al. Characterization of nonequilibrium condensation of supercritical carbon dioxide in a de laval nozzle[J].Journal of Engineering for Gas Turbines and Power，2018，140(4): 041701.

[6] SOAVE G.Equilibrium constants from a modified Redlich-Kwong equation of state[J].Chemical Engineering Science，1972，27(6): 1197-1203.

[7] SIRIGNANO W A.Compressible flow at high pressure with linear equation of state[J].Journal of Fluid Mechanics，2018，843:244-292.

[8] GRABOSKI M S，DAUBERT T E.A modified Soave equation of state for phase equilibrium calculations.3. Systems containing hydrogen[J].Industrial & Engineering Chemistry Process Design and Development，1979，18(2):300-306.

[9] BOBER W，CHOW W L.Nonideal isentropic gas flow through converging-diverging nozzles[J].Journal of Fluids Engineering，1990，112(4):455-460.

[10] BLUNDELL S J，BLUNDELL K M.Concepts in thermal physics[M].Oxford，UK: Oxford University Press，2009.

[11] PASSUT C A，DANNER R P.Correlation of ideal gas enthalpy，heat capacity and entropy[J].Industrial & Engineering Chemistry Process Design and Development，1972，11(4): 543-546.

[12] NIST.NIST chemistry WebBook，SRD69[DB/OL].Gaithersburg:National Institute of Standards and Technology，2018[2021-05-10].https://webbook.nist.gov/chemistry/fluid/.

[13] BEUNE A.Analysis of high-pressure safety valves[D]. Eindhoven，the Nethlands:Eindhoven University of Technology，2009.

[14] MORAN M J，SHAPIRO H N.Fundamentals of engineering thermodynamics[M].5th edit.Hoboken，NJ, US:John Wiley & Sons，2006.

[15] EDLEBECK J，NELLIS G F，KLEIN S A，et al.Measurements of the flow of supercritical carbon dioxide through short orifices[J].The Journal of Supercritical Fluids，2014，88:17-25.

[16] 马营，杨臻，赵蔚楠，等.内弹道多目标优化算法对比分析[J].兵工自动化，2021，40(3): 81-85.

MA Y，YANG Z，ZHAO W N，et al.Comparative analysis of multiple objective optimization algorithms for interior ballistics[J].Ordnance Industry Automation，2021，40(3):81-85. (in Chinese)