扬声器直流偏置产生机理研究及其估算方法

岳 磊，陆 晓,3,4，温周斌,2

（1.浙江中科电声研发中心，浙江嘉善 314115；2.中国科学院声学研究所东海研究站，上海 201815；3.中国科学院大学，北京 100049；4.中国科学院声学研究所，北京 100190）

0 引言

动圈式扬声器工作时，音圈往往会偏离平衡位置，其振动位移存在直流偏置。直流偏置会降低扬声器声压级灵敏度和本就不高的工作效率[1]、导致更严重的失真（尤其是偶次谐波失真）、增加扬声器工作的不稳定性，极端情况甚至会导致音圈跳出磁隙，对于振幅较大的超低音扬声器和短音圈的微型扬声器，直流偏置的影响尤为明显。

Wolfgang[2]通过测量扬声器的非线性特性和直流偏置，研究了扬声器非线性特性曲线对称性对直流偏置的影响，以及不同频段内影响直流偏置的主要因素。James 等[3]分析了磁阻力非线性特性对谐波失真和直流偏置的影响，提出一种补偿该影响的非线性控制算法。管善宁[4]分析了直流偏置的产生机理，给出不同频段非线性特性对直流偏置方向的影响，以及使用Klippel R&D 系统测量直流偏置的方法。朱国祥[5]以一款汽车扬声器为例探讨了直流偏置如何影响扬声器的工作点，以及直流偏置随激励信号频率和电压的变化规律。非线性特性是扬声器的重要特性，因而成为学者们普遍关心的问题，但相关研究主要集中在非线性特性对声压级和失真的影响[6-8]，较少与直流偏置紧密关联，亦未找见有关直流偏置估算方法的报道。

本文首先通过扬声器的驱动力系数、劲度系数和电感等主要非线性参数的多项式级数形式研究与之对应的驱动力、回复力和磁阻力中的直流分量的大小和方向，并进一步分析这些直流分量所导致音圈位移的直流偏置。然后提出一种基于集总参数模型（Lumped Parameter Model,LPM）的扬声器音圈直流偏置的估算方法。它先通过数值仿真分析方法或测量方法得到扬声器的驱动力系数Bl（x）、劲度系数K（x）和电感L（x）等非线性参数，再将这些参数代入到LPM 模型中，求解该模型并做后处理估算得到直流偏置。

1 非线性特性与直流偏置

动圈式扬声器主要由磁铁、前夹板、后夹板、导磁板柱、音圈、定心支片、防尘帽、锥盆和折环等组成。图1 是一款典型的动圈式扬声器的结构示意图[9]。

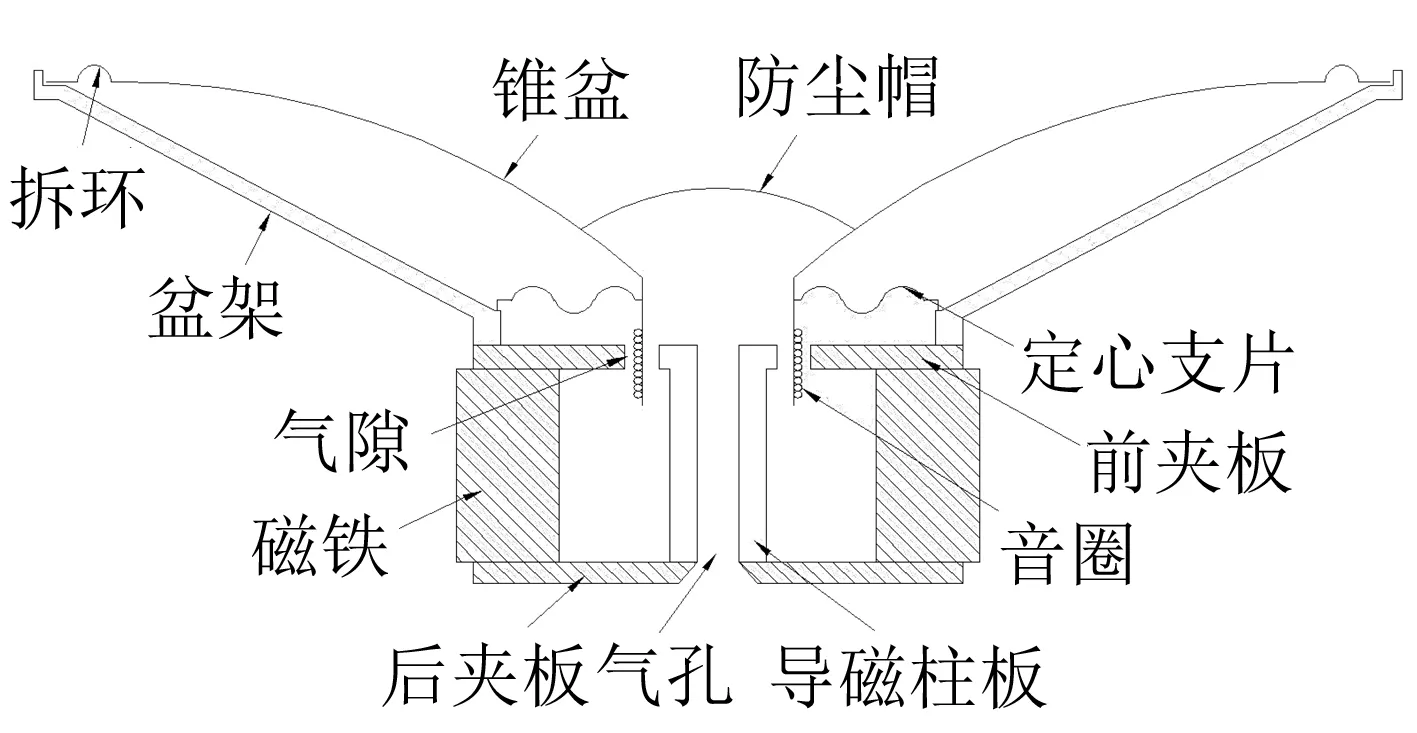
图1 典型的动圈式扬声器结构示意图 Fig.1 The schematic diagram of a typical moving-coil loudspeaker

扬声器工作时，通电的音圈在磁隙中上下运动。由于磁隙中的磁通量分布不均匀、悬吊系统（包括折环和定心支片等）的几何非线性和磁性材料分布不对称等原因，扬声器的驱动力系数Bl、劲度系数K和电感L等存在明显的非线性[10-11]，都是随振动位移x变化的非线性参数。图 2 是一款 6.5 in（1 in=2.54 cm）汽车扬声器的Bl（x）、K（x）和L（x）曲线图，也是大多数动圈式扬声器的非线性参数的典型曲线图。

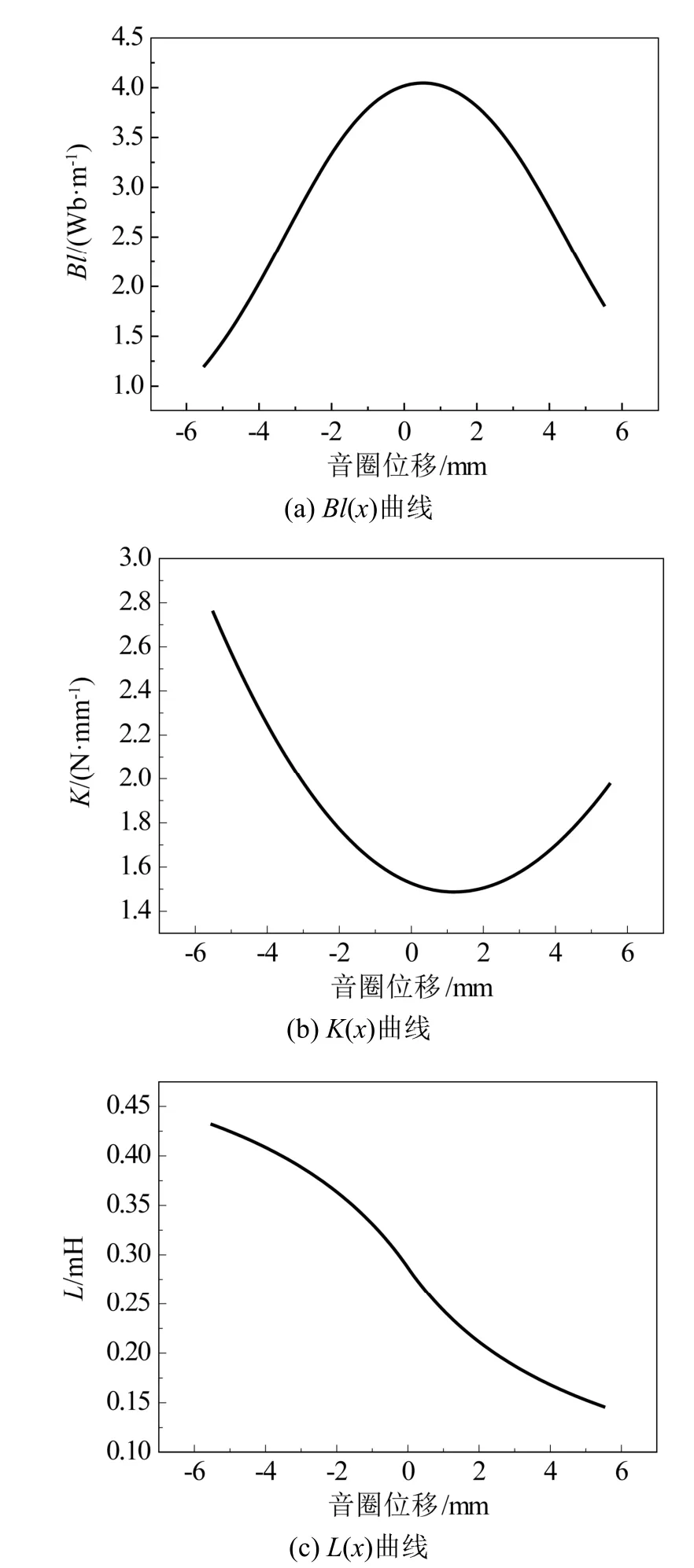
图2 扬声器的Bl（x）、K（x）和L（x）曲线 Fig.2 Bl(x)、K(x) and L(x) curves of loudspeaker

对于大多数扬声器，Bl（x）曲线可以近似看作是一条开口向下的抛物线，在初始位置附近有极大值，随着位移增大，驱动力系数Bl（x）减小；K（x）曲线则相反，它可以近似看作是一条开口向上的抛物线，在初始位置附近有极小值，随着位移增大，劲度系数K（x）增大；而L（x）曲线是一条随着位移单调递减的曲线。对于一些微型扬声器，它们的K（x）曲线可能会有所不同，但仍可以粗略地将视为抛物线。

当扬声器输入频率为f的激励信号时，流经音圈的电流和音圈的振动位移可分别表示为

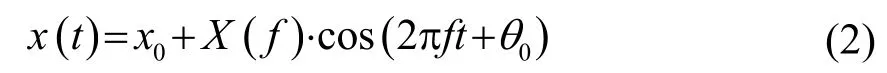
式中：x0是初始位移；I(f)和X(f)分别为电流和振动位移的幅值，它们都是随频率变化的，但在低频时的变化幅度较小。当f在扬声器的共振频率fs附近时，振动系统的共振会导致反向电动势增大，I(f)在fs附近会出现一个小的低谷；当f>fs时，由于电涡流[7]随着频率的增加而增加，阻抗逐渐增大，因此I(f)呈现逐渐下降趋势。因为扬声器振动系统的阻尼值很小，扬声器在工作时是处于欠阻尼状态，所以X(f)随f增大而缓慢增大，约在fs处出现最大值；当f>fs时，X(f)随f增大而下降。θ0是电流和位移的相位差，当ffs时，电流和位移是反相的[12]。

将Bl（x）、K（x）和L（x）分别表示为x的多项式级数展开式（忽略高次项）：

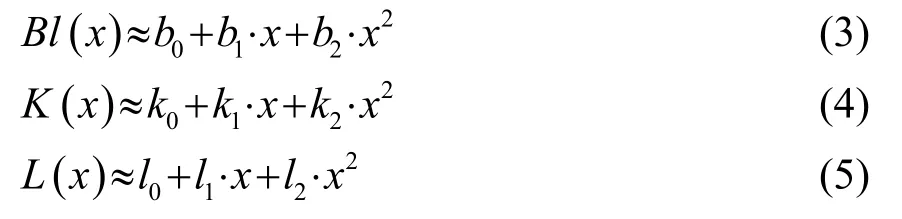
式中：b0、b1、b2、k0、k1、k2、l0、l1和l2均为多项式系数。因为Bl（x）是一条开口向下的准抛物线，所以b2是负数；b1的正负决定了该抛物线的对称轴位于x轴的正轴还是负轴。而K（x）是一条开口向上的准抛物线，故k2是正数；k1的正负决定了该抛物线的对称轴位于x轴的负轴还是正轴。电感是一条随着位移单调递减的曲线，则l1是负值。

对于动圈式扬声器，音圈所受到的驱动力是驱动力系数Bl（x）与电流i的乘积，即：

将式（2）代入式（3），再和式（1）一起代入式（6），则式（6）变为

为简化公式，在式（7）中分别用I和X代替了I(f)和X(f)。由式（7）可知，当动圈式扬声器在频率为f的激励信号作用下，驱动力除了包括基频响应信号和倍频谐波响应信号之外，还有一个与频率无关的直流信号，也即驱动力存在一个直流分量Fd,DC：

由式（8）可知，驱动力直流分量的方向（正负）取决于b1与cosθ0的乘积。如前所述，b1的正负决定了对称轴位于x轴的正轴还是负轴，θ0是电流与位移的相位差。当f0），如果b1为正（负），则驱动力直流分量的方向也为正（负），它会使得音圈偏向驱动力系数最大值的方向（也即对称轴的方向）；当f=fs时，电流和位移是正交的（cosθ0=0），驱动力直流分量为0；当f>fs时，电流和位移是反相的（cosθ0<0），如果b1为正（负），则驱动力直流分量的方向却为负（正），它会导致音圈偏向驱动力系数最大值的反方向（也即对称轴的反方向）。随着频率的增加，位移和电流的幅度都大幅减小，因此，在高频段，驱动力中直流分量的影响非常小。

当动圈式扬声器工作时，音圈还会受到振动系统的回复力Fr(x)的作用。Fr(x)是劲度系数K（x）和位移x的乘积：

将式（2）代入式（4），再将式（2）和式（4）一起代入式（9），可将回复力表示为随时间变化的形式：

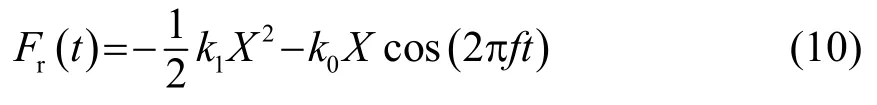
式（10）忽略了倍频谐波响应信号。由式（10）可知，这个回复力存在一个直流分量：

如前所述，k1的正（负）对应劲度系数的对称轴位于x轴的负轴（正轴）。因此，由式（11）可知，回复力的直流分量的方向会使得音圈偏向劲度系数极小值的方向（也即对称轴的方向）。但是，当f>fs时，因为位移振幅随频率增加而大幅下降，所以，在高频段，回复力中直流分量的影响也非常小。

电感L（x）决定了扬声器所受到的磁阻力Fm，Fm的计算公式[3]为

将式（1）和（2）代入式（12），也可将磁阻力表示为随时间变化的形式：

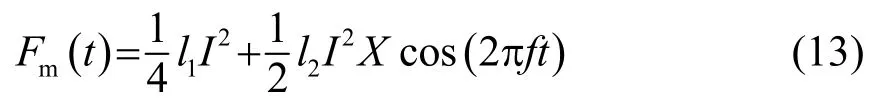
式（13）同样忽略了倍频谐波响应信号。由此可知，磁阻尼存在一个直流分量：

如前所述，l1是负值，故磁阻力直流分量也为负值。因而磁阻力的直流分量会使得音圈偏向电感大的方向。因为I(f)在fs附近会出现一个小的低谷，所以当f=fs时，磁阻力直流分量较小。当f>fs时，磁阻力直流分量影响较大，但随着频率增加，因为I(f)呈现逐渐下降趋势，磁阻力直流分量逐渐减小。

综上所述，由于扬声器驱动力系数、劲度系数和电感的非线性，会使得与之对应的驱动力、回复力和磁阻力存在直流分量Fd,DC、Fr,DC和Fm,DC。它们的作用各不相同，因此导致音圈偏离平衡位置而产生直流偏置的结果也不相同：

（1）当ffs时，Fd,DC会导致音圈偏向驱动力系数曲线的对称轴的反方向。以图2（a）为例，驱动力系数曲线对称轴在x轴的正轴上，则当ffs时，Fd,DC会导致音圈产生负的直流偏置。

（2）Fr,DC会使得音圈偏向劲度系数曲线的对称轴方向。以图2（b）为例，劲度系数曲线的对称轴也在x轴的正轴上，则Fr,DC会使得音圈产生正的直流偏置。

（3）Fm,DC会使得音圈偏向电感大的方向，即产生负的直流偏置。

（4）在高频段，Fd,DC和Fr,DC的影响非常小，Fm,DC成为音圈产生直流偏置的主因。

当动圈式扬声器工作时，音圈还将受到动生电动势Uv和感生电动势Uφ的作用。它们随时间变化的形式为

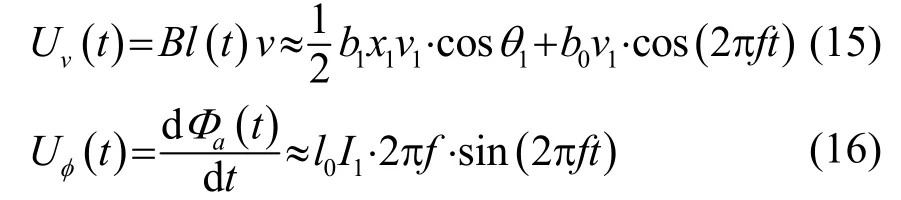
在式（15）中，忽略了倍频谐波响应信号。θ1是位移与速度的相位差，因位移与速度的相位是正交的（cosθ1=0），故动生电动势无直流分量。而由式（16）可知，感生电动势也无直流分量。

2 直流偏置的估算方法

采用集总参数模型研究和计算扬声器的各种特性是一种常用方法，具有快速和便捷等优势和特点。本文提出了一种基于LPM 模型的扬声器直流偏置的估算方法，首先采用数值仿真分析方法或者测量方法得到扬声器的Bl（x）、K（x）和L（x）等非线性参数，再将这些参数代入到LPM 模型中，求解该模型得到位移时域响应，取其平均值即可估算得到该扬声器的直流偏置。

动圈式扬声器的等效电路图[12]如图3 所示，其中，U为扬声器端电压、i为音圈中的电流、Re为音圈直流阻，由L2和R2组成的并联电路表示磁路中的电涡流损耗，v为音圈轴向振动速度；Cms(x)为扬声器振动系统顺性，Cms(x)=1/K(x)；Mms为等效振动质量、Rms为振动系统机械阻、Fm为磁阻力；Za为声辐射阻[13]，它在中低频段的值很小，这里忽略其对直流偏置的影响。

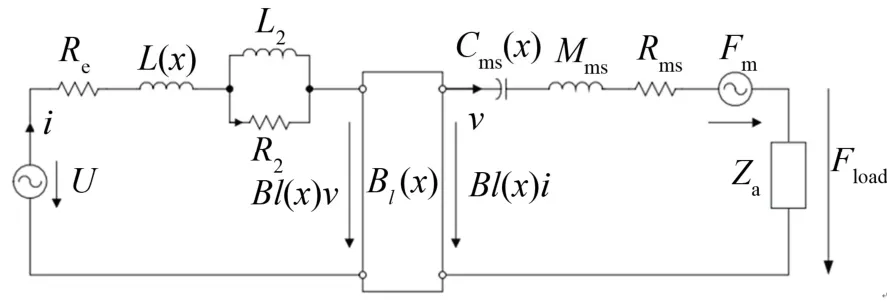
图3 动圈式扬声器的等效电路图 Fig.3 Equivalent circuit diagram of moving-coil loudspeaker

当输入电压U=U0⋅s in (2πf)（其中U0为电压幅值，f为信号频率），根据基尔霍夫电压定律，可给出电压平衡方程：

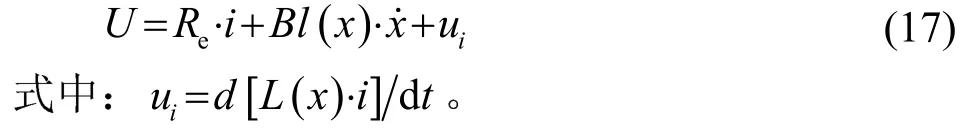
根据受力平衡原理，可给出运动方程：

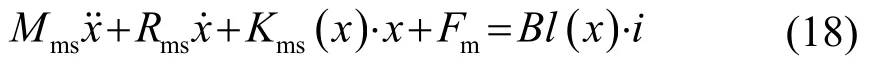
采用四阶龙格-库塔法[14]求解由方程（17）和（18）构成的常微分方程组，便可求解得到扬声器的振动位移x（t），其平均值即为扬声器的直流偏置。需要注意的是，应选取x（t）到达稳定阶段后的数据计算平均值，以避免瞬态过渡期对计算结果造成的误差。

采用本文提出的直流偏置估算方法估算了一款6.5 in 汽车扬声器和一款2 in 全频带扬声器的直流偏置，它是先基于COMSOL Multiphysics 有限元仿真软件仿真得到这两款扬声器的Bl（x）、K（x）和L（x）等非线性参数。图4 给出了6.5 in 汽车扬声器直流偏置的估算结果（黑色曲线），该扬声器共振频率fs约为68 Hz。

由图4 可知，在低于共振频率fs的频段，它的直流偏置为正（即音圈偏向磁隙外部），在共振频率附近达到最大值，最大值约为0.6 mm；从fs～150 Hz 附近，直流偏置由正的最大值迅速变为负的最大值，负的最大值约为−0.37 mm。该扬声器（低频）最大位移幅值约为3 mm，最大直流偏置已达最大位移幅值的12.3%，会对扬声器特性造成严重影响。在200 Hz～1 kHz 频段内，直流偏置逐渐减小，到1 kHz 时已减小到−0.1 mm 左右。

为了深入研究Bl（x）、K（x）和L（x）等三个非线性参数对总的位移直流偏置的贡献量，图4 还给出了仅考虑Bl（x）、K（x）和L（x）等三个非线性参数中的某一个所估算得到的位移直流偏置。在估算仅考虑某一非线性参数时，其他非线性参数都以x=0 处的数值（即忽略它的非线性）代入到方程中。

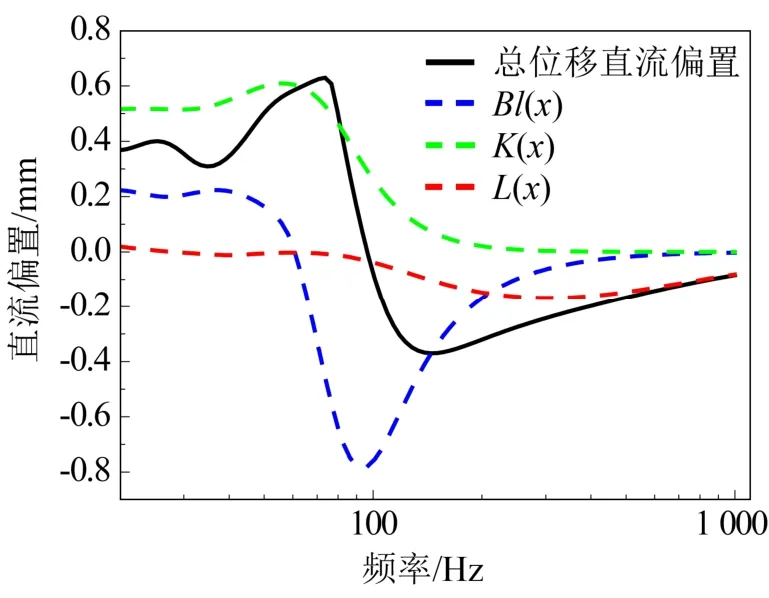
图4 单一非线性参数对总直流偏置的贡献量 Fig.4 The contribution of each nonlinear parameter to total DC offset of vibration displacement

为了深入研究Bl（x）、K（x）和L（x）等三个非线性参数对总直流偏置的贡献量，图4 还给出了仅考虑Bl（x）、K（x）和L（x）等三个非线性参数中的某一个所估算得到的直流偏置。在估算仅考虑某一非线性参数时，其他非线性参数都以x=0 处的数值（即忽略它的非线性）代入到方程中。

由图4 可知，由于驱动力系数的非线性特性，音圈在不同频段会产生不同的直流偏置：在低于共振频率的频段，音圈会产生正的直流偏置，其大小约为0.22 mm；在共振频率处直流偏置为0；在高于共振频率的频段，直流偏置为负，最大直流偏置约为−0.8 mm；随着频率增大，直流偏置大幅减小，到1 kHz 已几乎减小为0。劲度系数的非线性会使得音圈在全频段产生正的直流偏置，它在共振频率处出现最大值，最大直流偏置约为0.6 mm；随着频率增大，直流偏置大幅减小，到1 kHz 时，几乎接近0。与劲度系数相反，电感的非线性会使得音圈在全频段产生负的直流偏置：在共振频率附近会出现小幅波动，在300 Hz 附近出现极小值，约为−0.17 mm；随着频率升高，直流偏置逐渐减小。上述直流偏置的估算结果与前文的理论分析结果基本完全一致。

根据扬声器各非线性参数在不同频段对直流偏置的影响，合理利用或调整其非线性特性，可以调整或降低该扬声器振动位移的直流偏置：

（1）在低于共振频率的频段，劲度系数的非线性是导致直流偏置的主要原因，驱动力系数非线性的贡献量次之，而电感非线性的贡献量非常小。可提升劲度系数非线性曲线的对称性，减小k1值，从而可降低该频段的直流偏置；

（2）在共振频率附近，直流偏置由最大值迅速减小到最小值，驱动力系数非线性成为导致直流偏置的主要原因，劲度系数非线性的贡献量变为次要，而电感非线性的贡献量仍然最小。可提高驱动力系数非线性曲线的对称性、减小b1值，从而可降低该频段的直流偏置；

（3）在高于共振频率的高频段，劲度系数和驱动力系数的非线性的影响都较小，电感的非线性对直流偏置的贡献变为最大。可减小电感非线性曲线的斜率，减小l1值，从而可降低该频段的直流偏置。

3 测量验证

为了验证本文所提直流偏置估算方法的正确性和准确性，对上述6.5 in 汽车扬声器和2 in 全频带扬声器做测量比对研究，每款扬声器都挑选5 只样品做实验。采用Klippel R&D 系统的DIS 模块测量每个扬声器样品的直流偏置。与此同时，采用该系统的LSI 模块测量每个扬声器的Bl（x）、K（x）和L（x）等非线性参数。并且，利用测量得到的这些非线性参数，同样采用本文所提直流偏置估算方法估算得到所对应扬声器样品的直流偏置。

图5 给出了6.5 in 汽车扬声器直流偏置的估算结果和测量结果。其中，估算1 是利用COMSOL软件仿真得到非线性参数进行估算得到的该款扬声器的直流偏置频响曲线；估算2（1#～5#）则是利用Klippel 测量系统分别测量1#～5#扬声器样品的非线性参数进行估算得到对应1#～5#扬声器样品的直流偏置频响曲线；1#～5#测量则是采用Klippel 测量系统直接测量得到的直流偏置频响曲线。由图5 可知，估算结果与测量结果总体趋势较为一致。5 只 扬声器样品的直流偏置测量结果在数值上存在一定的差异，它们对应的基于测量参数估算的结果在共振频率fs以下的低频段也存在一定的差异。

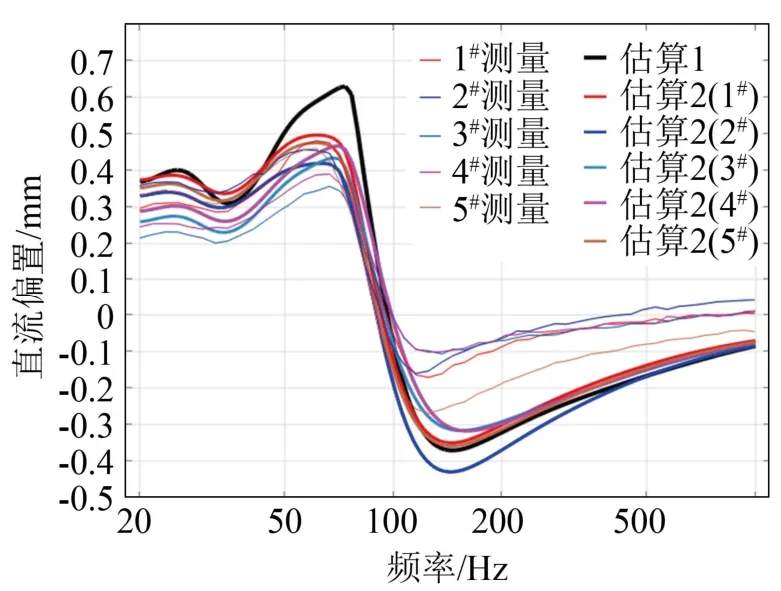
图5 一款6.5 in 汽车扬声器直流偏置的估算结果和 测量结果 Fig.5 Measured and predicted results of the DC offset of vibra-tion displacement for a 6.5 in automobile loudspeaker

图6 给出2 in 全频带扬声器直流偏置的估算结果和测量结果。与6.5 in 汽车扬声器相类似，估算结果与测量结果总体趋势比较一致。值得一提的是，这款2 in 全频带扬声器的直流偏置很小，只有几微米～几十微米数量级。

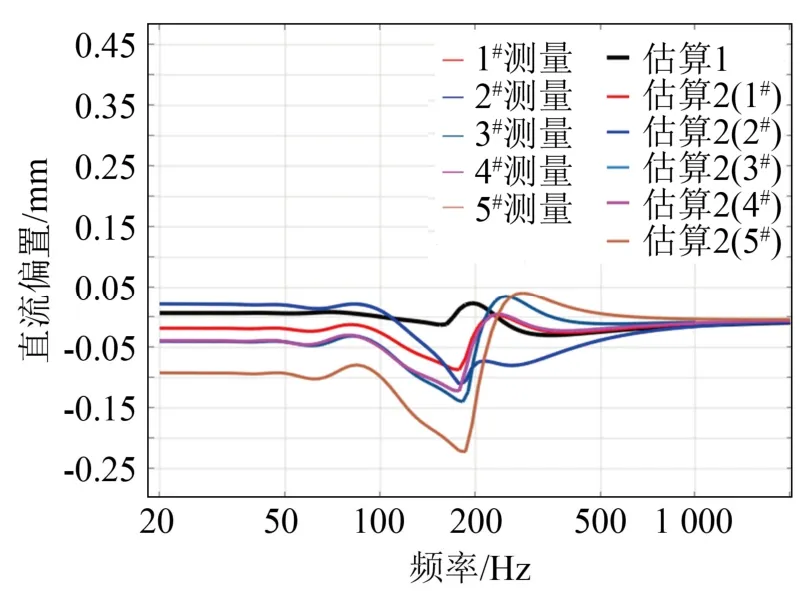
图6 一款2 in 全频带扬声器直流偏置的估算结果和 测量结果 Fig.6 Measured and predicted results of DC offset of vibration displacement for a 2 inch full range loudspeaker

需要指出的是，由于制造工艺和材料特性等因素，扬声器样品个体间存在一些差异。更为重要的是，扬声器是一个非线性系统。线性系统不同，非线性系统模型参数的微小变化或误差都可能会对系统特性产生较大的影响。由于仿真建模中的几何模型和材料参数的输入误差，或者Klippel R&D 系统的测量误差，无论是利用仿真分析方法，还是利用测量方法获取的非线性参数都会存在一定误差。因此，基于LPM 模型的直流偏置估算结果与实测的直流偏置仍存在一定误差，但本文提出的估算方法依然是有效可行的。

4 结论

研究结果表明扬声器驱动力系数、劲度系数和电感的非线性会使得音圈受到与之相对应的驱动力、回复力和磁阻力中的直流分量的作用，从而使得音圈被推离初始（平衡）位置，产生直流偏置。采用所提出的基于LPM 模型的估算方法估算得到扬声器直流偏置曲线与实测曲线趋势基本一致。合理调整扬声器的非线性特性，可以调整或减小直流偏置，达到设计高品质扬声器的目的。