一种空间匹配的高速飞行目标轨迹估计方法
2022-07-29李弘毅顾亚平
邓 步,李弘毅,顾亚平
(1.中国科学院声学研究所东海研究站,上海 201815;2.中国科学院大学,北京 100049)
0 引言
相对于光学和雷达目标探测,低空目标声探测采用被动探测方法,受环境影响较小,因此受到广泛关注[1-3]。当目标离测点阵列的距离较近时,可将传感器阵列所获得的信号视为满足球面波,此时可将测得的信号到各个阵元的时间差作为先验信息 进行参数估计,得到运动参数[4]或定位参数[5-6]。当目标离测点阵列的距离较远时,声信号视为平面波,进而测得信源方位[7],再利用阵列网络进行定位[8]。
文献[9]提出了一种基于声多径传播模型的目标运动参数估计方法。该方法利用不同路径声信号的到达时间估计值,实现对目标运动参数的估计,该方法要求布设尽可能多的长基线声传感器阵。
文献[10]对瞬时频率方法进行了拓展,提出了一种基于单声传感器阵列的目标运动轨迹估计方法。该方法首先利用多普勒效应估计目标飞行参数,结合波达方向(Direction of Arrival,DOA)估计目标轨迹方向、水平偏置和高度,依据几何模型确定其运动轨迹。该方法主要适用低速飞行目标。
文献[11]提出了基于五元十字阵的低空目标声测无源定位算法。在时延估计方面,该文献提出了基于维纳加权的频域自适应时延估计算法和基于双谱的时延估计算法。在小尺寸高精度定向方面,该文献首次将压差式矢量声传感器引入低空目标侧向研究中,提出基于矢量传感器阵的宽带相干信号子空间最优波束形成算法。
文献[12]利用布设于有限空间内的声传感器阵实现低空高速目标跟踪为背景,通过对某典型低空高速目标噪声波形的分析,发现其噪声呈现宽带低频谱特征。因此,该文献主要研究了基于时延估计的目标定位跟踪方法,提出了多面交汇的目标轨迹估计方法。
目前对低空飞行目标的研究主要集中在直升机、无人机等低速目标,而低空高速飞行目标威胁性更高,且更加难以跟踪。高速飞行目标的噪声是一类瞬态信号[10],难以准确获取其信号特征,给定位跟踪带来了较大困难。
影响高速目标轨迹测量精度的原因很多,但主要因素有:(1)目标高速运动,会产生多普勒频移;(2)环境中的风速是时变的,且风向具有不确定性,造成声音传播各向异性。两者均会引起阵列中阵元的测量误差。
因此,在对高速飞行目标进行波达方位估计时,不可避免地存在估计误差。同时,当目标高速运动的速度接近声速时,在某一时刻上,不同阵列所接收到的信号并非信源在同一时刻所发出,难以在时间维度上进行对齐。针对上述问题,借鉴点云数据处理的思想[13],本文在探测范围内建立字典,提出了一种基于空间匹配的轨迹估计方法。仿真结果表明,在一定误差范围内,轨迹估计结果依然表现良好,达到预期目的。
1 字典建立
假设目标的探测范围已知,即目标出现在100 m×100 m×200 m 的空间范围内,在探测区域顶点处安装相同的测向阵列,如图1 所示。目标从任意方向飞过探测区域时,至少从两个阵列之间穿过。将阵列1 位置视为坐标原点。每个阵列从字典建立到平面拟合流程一致,本文以阵列1 进行推导说明。
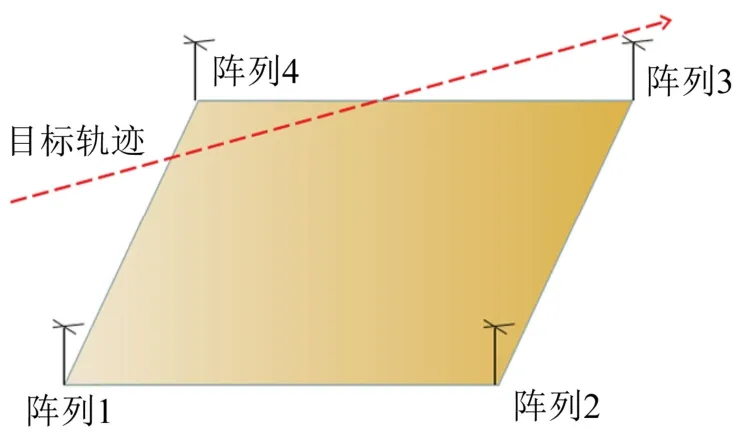
图1 目标探测区域示意图 Fig.1 Schematic diagram of target detection area
将空间内水平和垂直距离以设定间距d1为间隔进行划分,即若d1=1 m,该空间被划分为2×106个具有独立坐标的确定的空间点,表示为:(xi,yi,zi),i=1,2,…,N。空间点示意图如图2 所示。
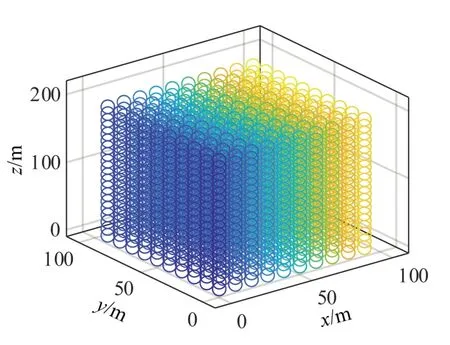
图2 空间点示意图 Fig.2 Space point diagram
每个点相对于位于原点的阵列1 的方位角与俯仰角可通过坐标转换公式进行转换,投影到极坐标下。将N个空间点的方位角θ与俯仰角ϕ构成字典进行数据存储。即:

2 轨迹估计
将接收到的信号进行分帧处理,计算每一帧数的波达方位,设有K帧数据,结果表示为
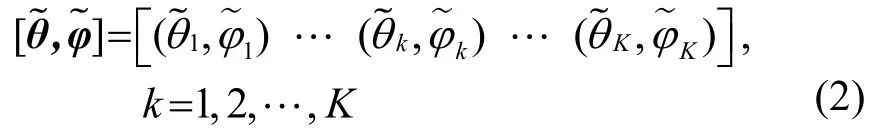
计算每帧数据得到的波达方向与字典中每个空间点方位角与俯仰角的均方误差,表示为
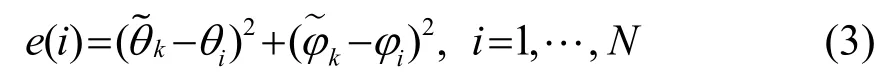
单帧数据计算得到的波达方位与空间点字典产生N个误差结果。再进行最小误差匹配,即将计算得到的误差进行排序,搜索误差最小的n个点进行存储,表示为
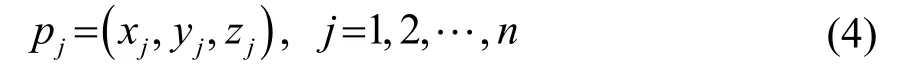
当n=100 时,最小误差分布图如图3 所示。从图3 中可以看到,匹配得到的n个误差最小空间点在空间中沿着一定方向进行分布且分布密度与空间点和阵列1 的几何距离成正比。
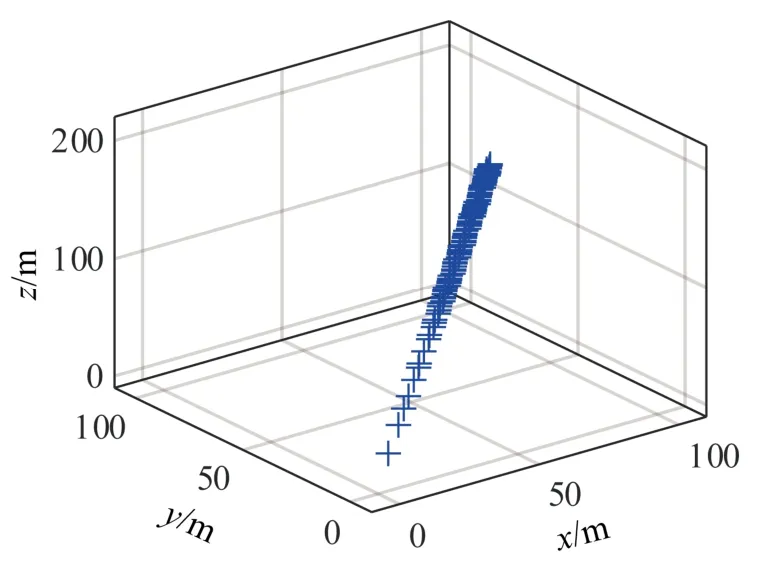
图3 最小误差分布图 Fig.3 Schematic diagram of the minimum error distribution
2.1 三维空间直线拟合
本文使用整体最小二乘法[14-15],对单帧数据得到的n个误差最小空间点进行拟合,以获得空间直线的几何参数,为后续平面拟合做准备。
将空间直线的点向式方程变形为

式中:x0、y0、z0为空间直线的已知点;A、B、C为待求参数。
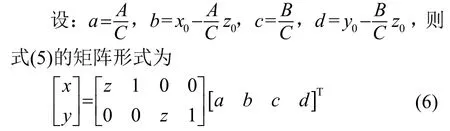
设V为拟合误差,I为单位矩阵,对存储的n个误差最小空间点进行构造误差方程。根据最小二乘理论中的间接平差模型[16],令:

则误差方程表示为

整体最小二乘法是同时顾及观测值和系数矩阵误差的一种平差方法,相比于最小二乘法,其参数估值是统计最优解。本文采用易于编程实现的整体最小二乘迭代法,解算式(8)中的空间直线的误差方程,平差准则为
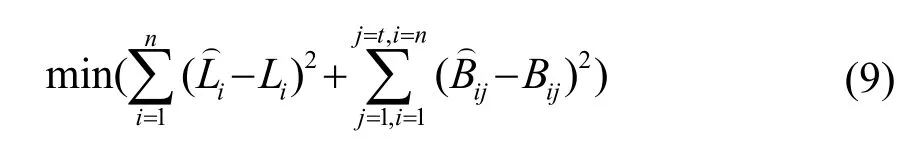
代入式(8),对系数矩阵B和参数向量X中各元素进行求导,获得迭代方程式:
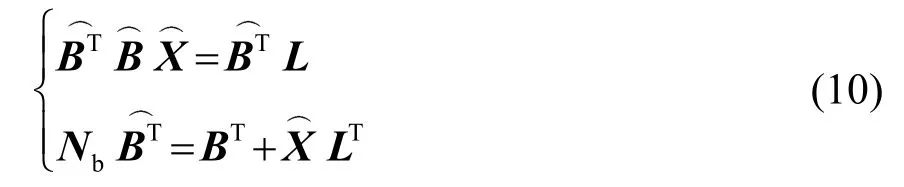
其中:

设初始值为X0,使用整体最小二乘迭代法对误差最小的n个点进行拟合,结果如图4 所示。
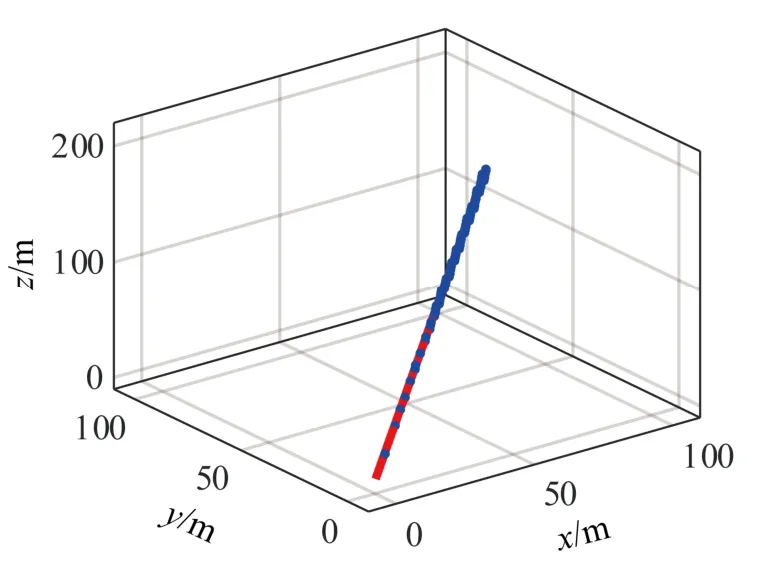
图4 整体最小二乘直线拟合结果 Fig.4 The result of overall least squares linear fitting
该直线的方向向量可视为目标与阵列坐标的矢量方向,即可视为真实目标位置估计点位于该拟合直线上。
同理对K帧数据连续进行上述处理,拟合结果如图5 所示。
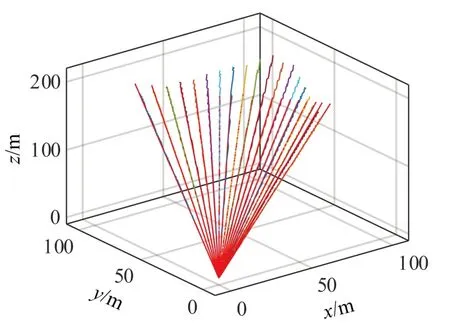
图5 对K 帧数据进行的整体最小二乘直线拟合结果 Fig.5 The result of overall least square linear fitting for the K-frames of data
2.2 稳健最小二乘平面拟合
由于高速飞行目标在探测范围内为直线运动,在一个阵列的条件下,多帧最小二乘拟合直线理想情况下共面,即均在同一个平面上。理想条件下,两条共面直线即可确定平面,但在2.1 节中对直线进行拟合时存在一定误差,因此直线共面条件不可能实现。此时使用空间直线上的采样点来对平面进行拟合,得到由方向直线构成的近似平面。本文在每帧数据所确定的直线上均匀采样100 个点构成空间点数据集M,该数据集中不存在异常点,受文献[13,17-18]启发,采用一种稳健最小二乘平面拟合方法。理论上,两帧数据所构成的空间点数据集即可确定相应平面。
使用多项式函数表示平面:
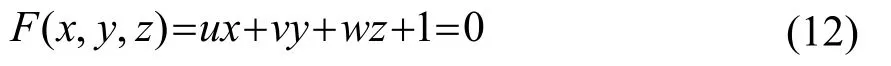
式中:u、v、w为待求参数。
设数据集:
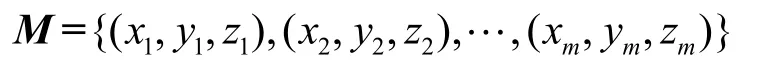
其最佳拟合平面应满足:
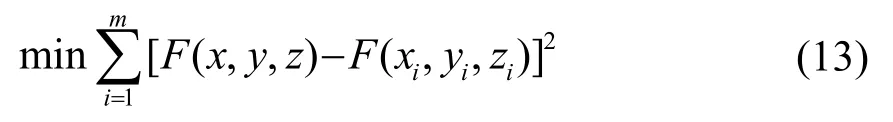
由式(12),式(13)可以表示为
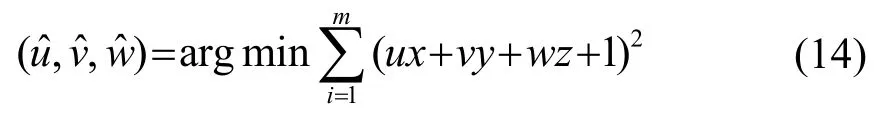
对式(14)中的u、v、w求偏导使其为0。整理后设:
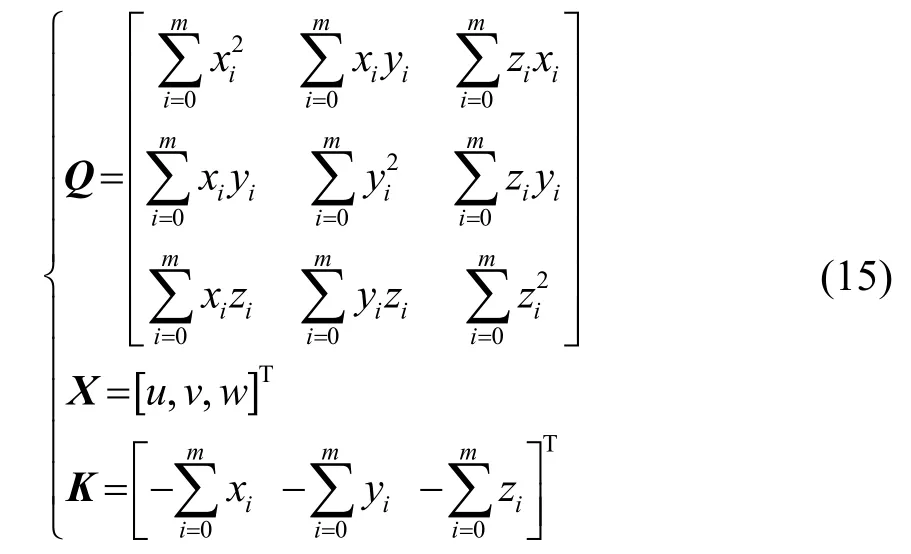
则可得:

可解得平面方程系数为

设Di为数据集M中点到拟合平面的距离,为数据集M中点到拟合平面的平均距离。精度评定距离标准偏差为

利用式(17)求得的u、v、w对平面特征向量进行初始化,计算出数据集M中每个点至拟合平面的距离Di。当Di≥ 2σ时,此点被认为是异常点并删除;反之,则保留。再利用所有保留下来的点通过式(13)—式(18)重新计算进行迭代,直到剩下所有点的Di都在规定的阈值之内,即Di都小于标准偏差的2 倍时为止,获得最佳的u、v、w构造平面特征向量,进而获得拟合平面。
对2.1 节中所得拟合直线进行平面拟合,结果如图6 所示。
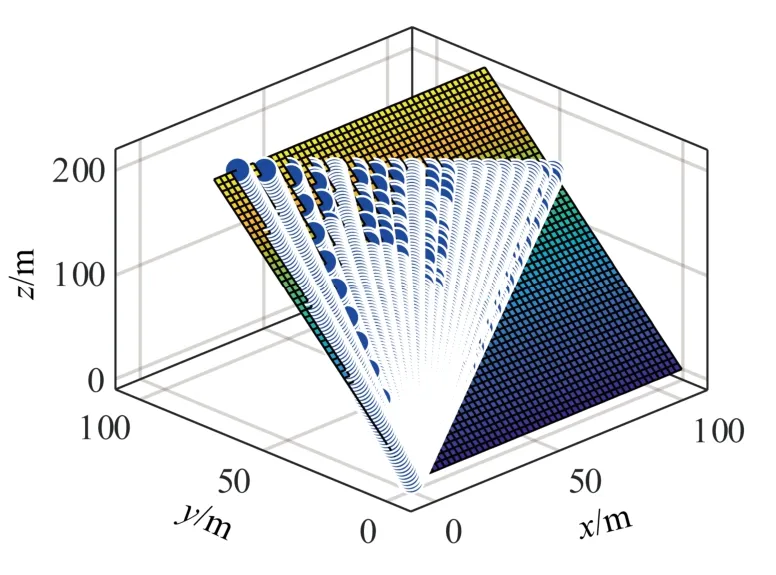
图6 拟合直线的平面拟合 Fig.6 Plane fitting by fitted lines
2.3 轨迹估计
由图1 可知,目标从任意方向进入探测区域时,始终位于至少两个阵列的中间区域。高速飞行目标在探测区域内可以视为直线运动,而空间中两个不平行平面即可确定一条相交直线,即为估计得到的目标运动轨迹,算法流程图如图7 所示。

图7 估计目标飞行轨迹的算法流程图 Fig.7 Algorithm flowchart for target flying trajectory estimation
设阵列1 位于坐标点(0,0,0),阵列3 位于坐标点(0,100,0),对于单个阵列,分别使用两帧数据与多帧数据进行轨迹估计,目标轨迹估计与显示如图8、9 所示。
如图8(a)、8(b)所示,两平面交线即为估计轨迹。如图9(a)、9(b)所示,红色点为真实轨迹点,绿色点为本文算法估计得到的轨迹点。仿真结果验证了两个阵列分别仅使用两帧数据即可估计出目标轨迹。可以通过增加使用的数据帧数提高估计精度,该方法可较为准确地对目标进行轨迹估计。
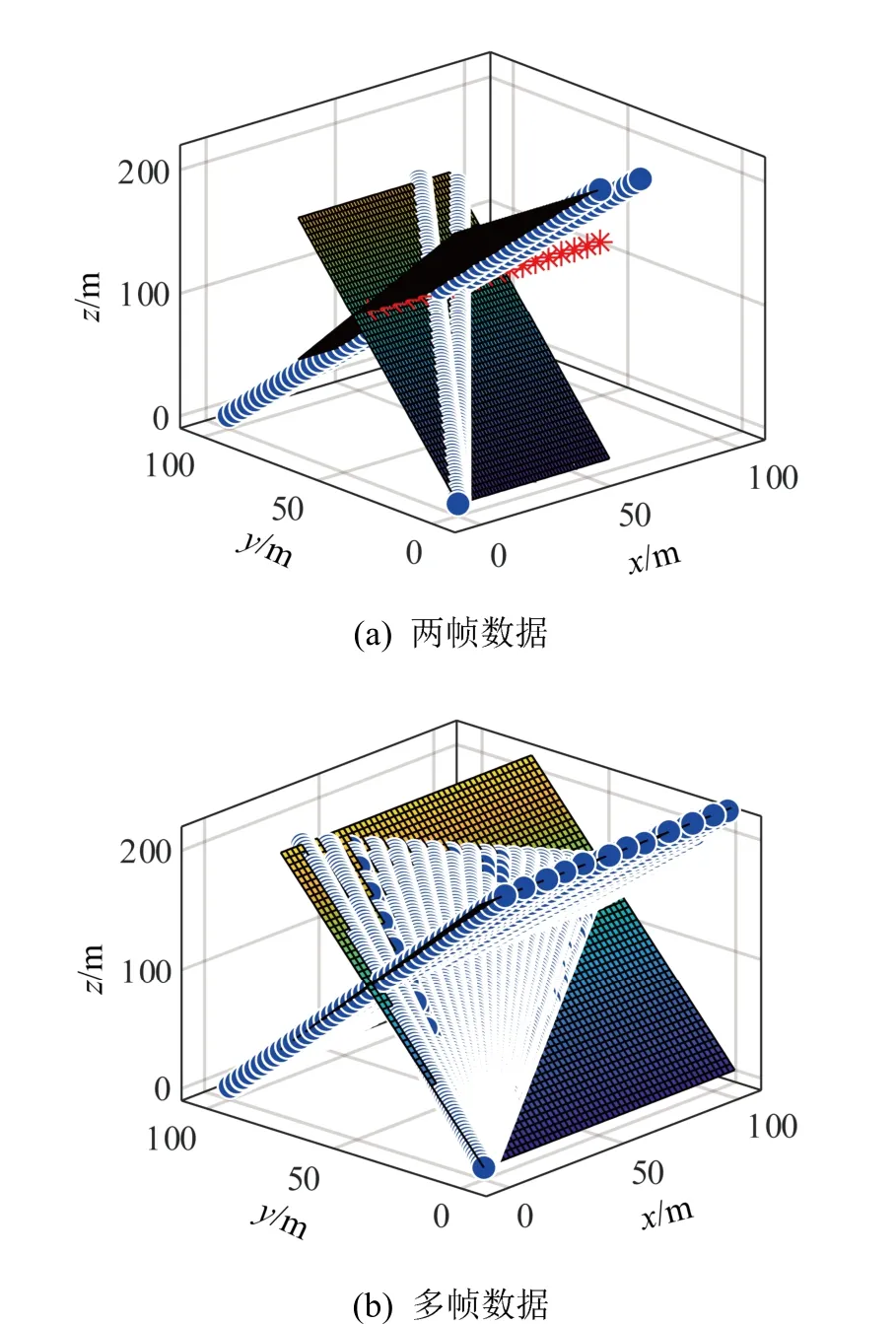
图8 不同帧数据的轨迹估计结果 Fig.8 Trajectory estimation results by different frames of data
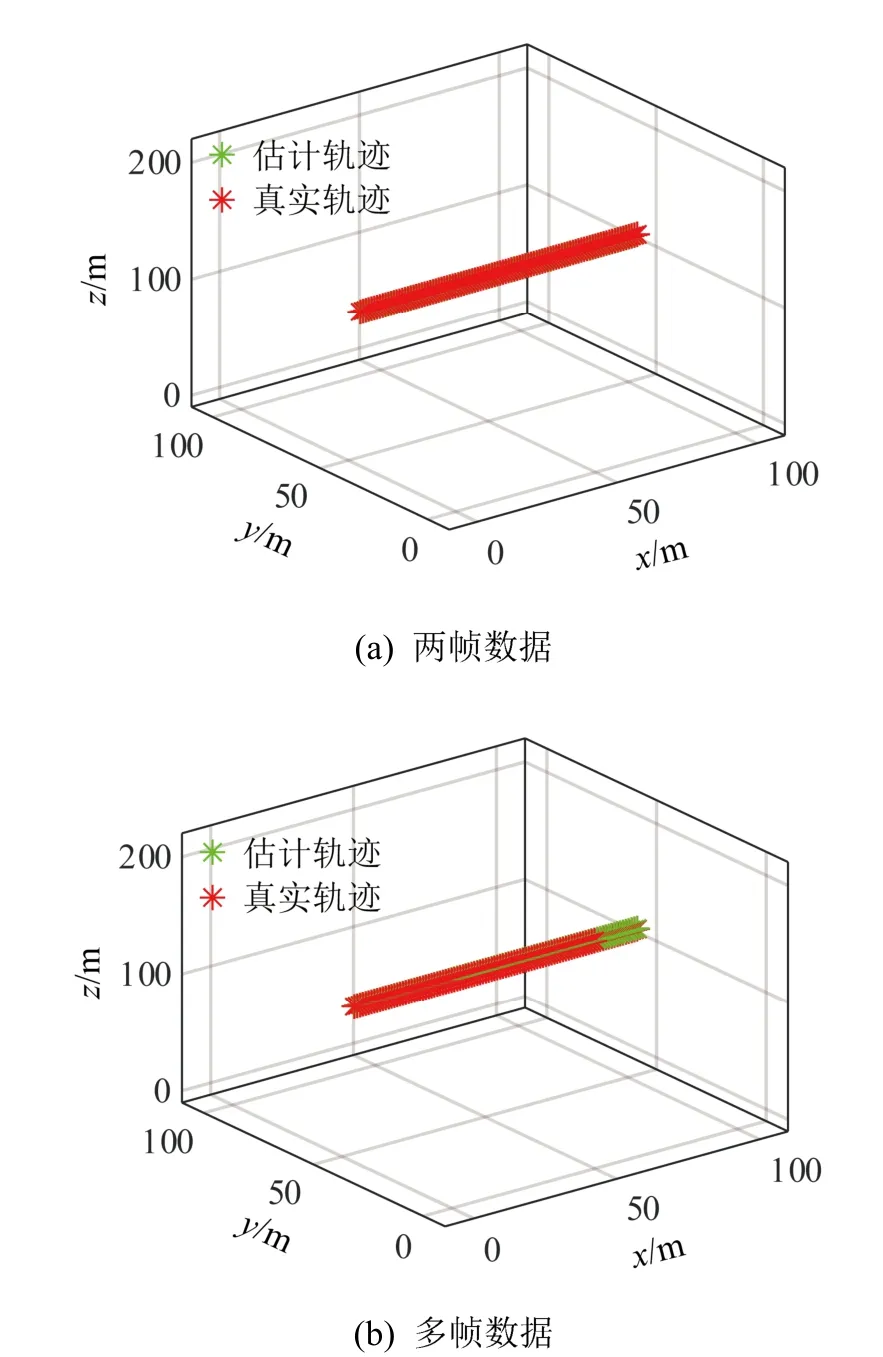
图9 真实轨迹与估计轨迹 Fig.9 Real trajectory and the estimated trajectory
3 误差分析
3.1 轨迹误差
高速飞行目标在探测范围内为直线运动,轨迹估计结果也为空间中的直线方程。由于探测范围已知,设在x轴上[0,100]范围内,同样以d1为间隔,对估计的轨迹ME与真实轨迹MT进行采样,数据点数为n,分别表示为
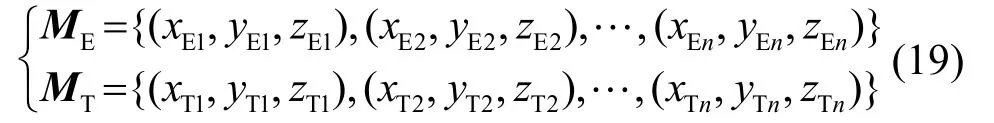
轨迹估计误差表示为
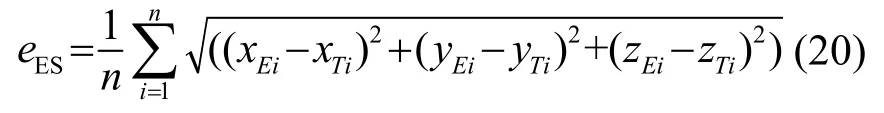
3.2 数据帧数对误差的影响
由于直线拟合与空间拟合均存在误差,估计得出的轨迹误差与数据帧数有直接关系,如表1 所示。

表1 数据帧数对轨迹估计误差影响 Table 1 The influence of the number of data frames on the trajectory estimation error
3.3 单阵列安装误差对轨迹估计结果影响
由2.3 节可知,使用两个阵列(阵列1、阵列2)即可估计出目标轨迹。若忽略阵列1 误差,阵列2 由于阵列设备安装产生方位估计误差。设阵列2 对每帧数据进行方位估计误差相同,俯仰角与方位角误差范围均为[− 3°,3°],误差分辨率为0.1°。目标飞行高度分别为60.9、90.9、120.9 m,误差结果如图10 所示。
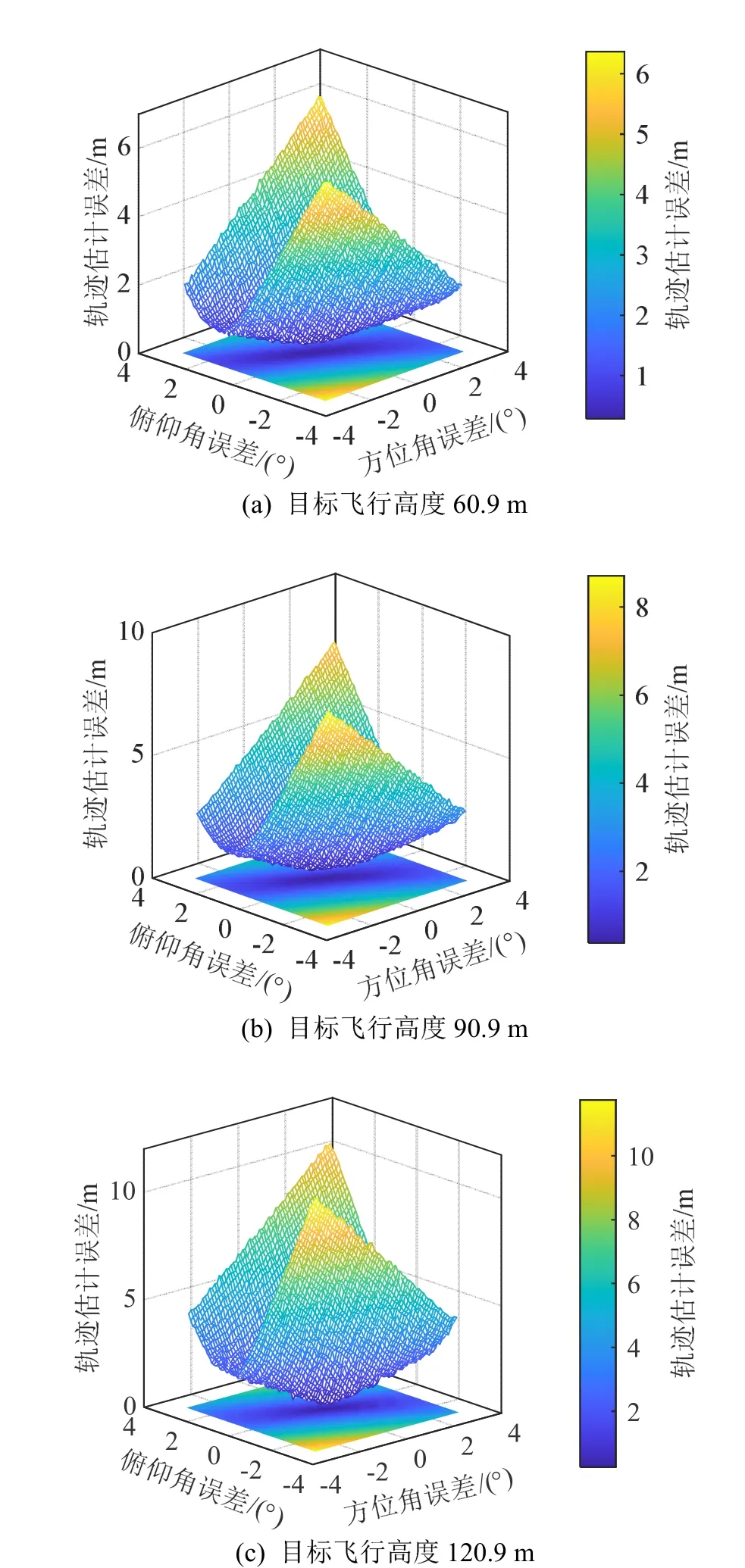
图10 单阵列波达方位估计误差对轨迹估计误差的影响 Fig.10 Influence of DOA estimation error of a single array on trajectory estimation error
3.4 双阵列安装误差对轨迹估计结果影响
若考虑阵列1、2 由于阵列设备安装产生的方位估计误差。设阵列1、2 对每帧数据进行方位估计误差相同,俯仰角与方位角误差范围均为[− 3°,3°],误差仿真步长为0.1°。目标飞行高度分别为60.9、90.9、120.9 m,误差结果如图11 所示。
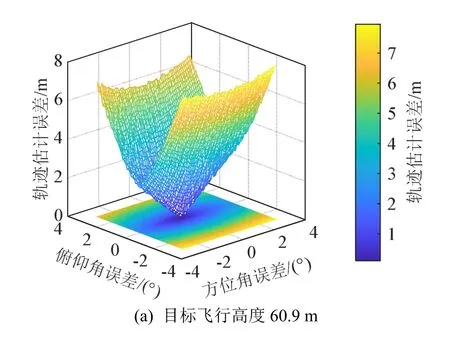
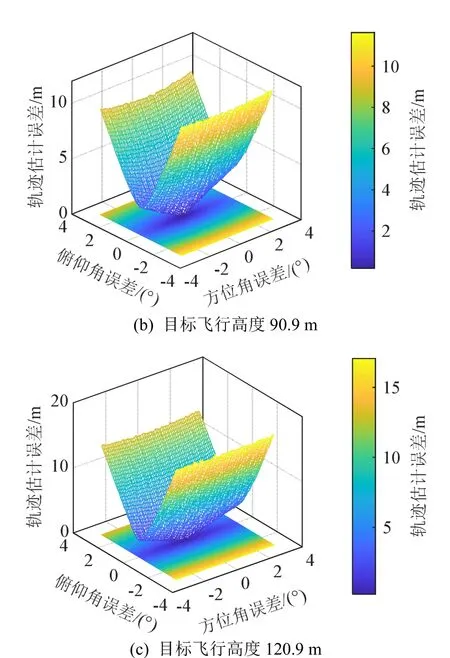
图11 双阵列波达方位估计误差对轨迹估计误差的影响 Fig.11 The influence of double-array DOA estimation error on trajectory estimation error
3.5 双阵列随机误差对轨迹估计结果影响
同时考虑阵列1、2 产生的波达方位估计误差对轨迹估计造成的影响。设阵列1、2 对每帧数据进行波达方位估计误差为随机误差,设俯仰角、方位角随 机误差 范围均 为[− 5 °,5 °]、[− 7 °,7 °]、[− 9 °,9 °],误差仿真步长为0.1°,进行蒙特卡洛仿真。轨迹估计误差数值分布与轨迹估计误差统计分布如图12~14 所示,轨迹估计平均误差与最大误 差如表2 所示。
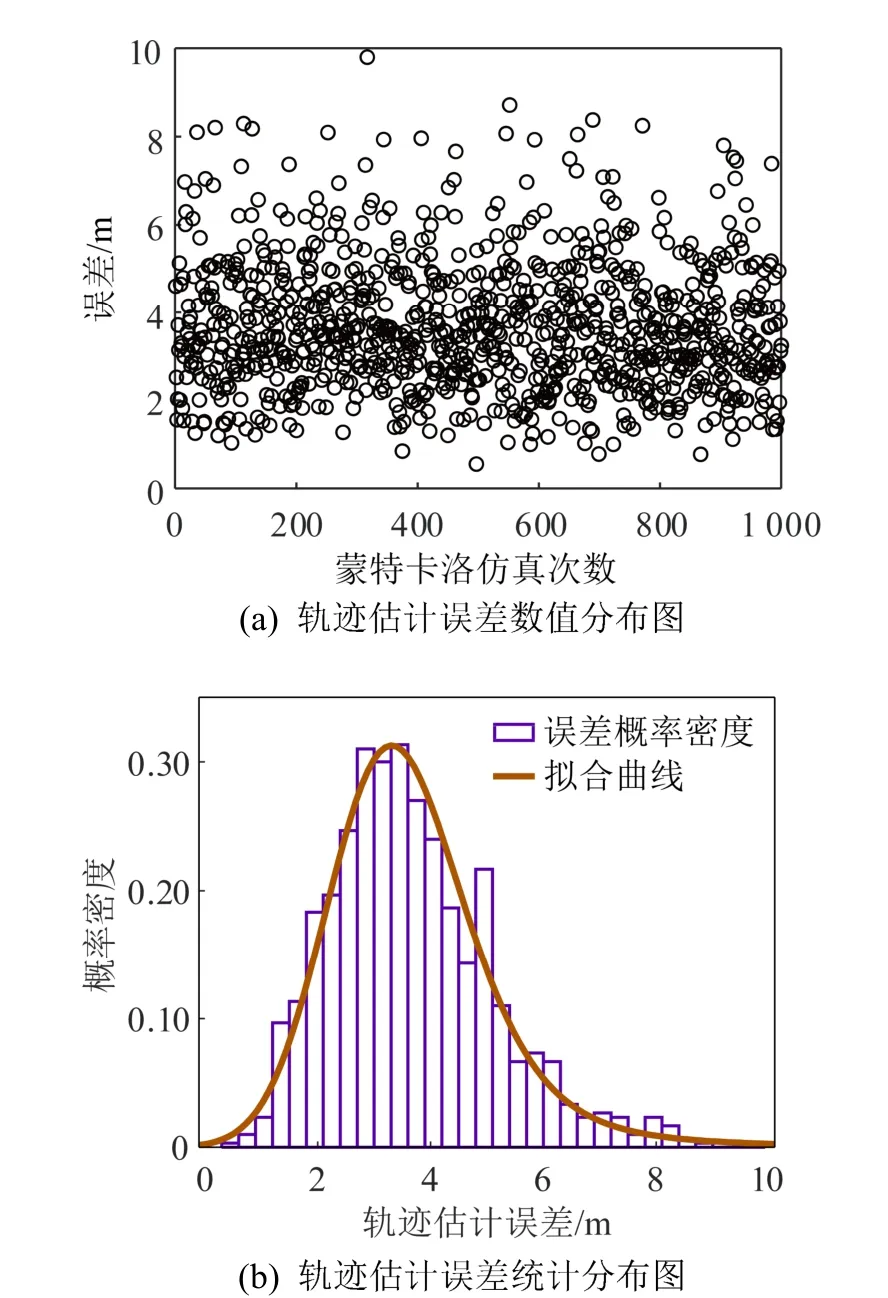
图12 波达方位估计随机误差在[-5°,5°]对轨迹估计影响 Fig.12 Influence of the random error of DOA estimation on the trajectory estimation in [-5°,5°]
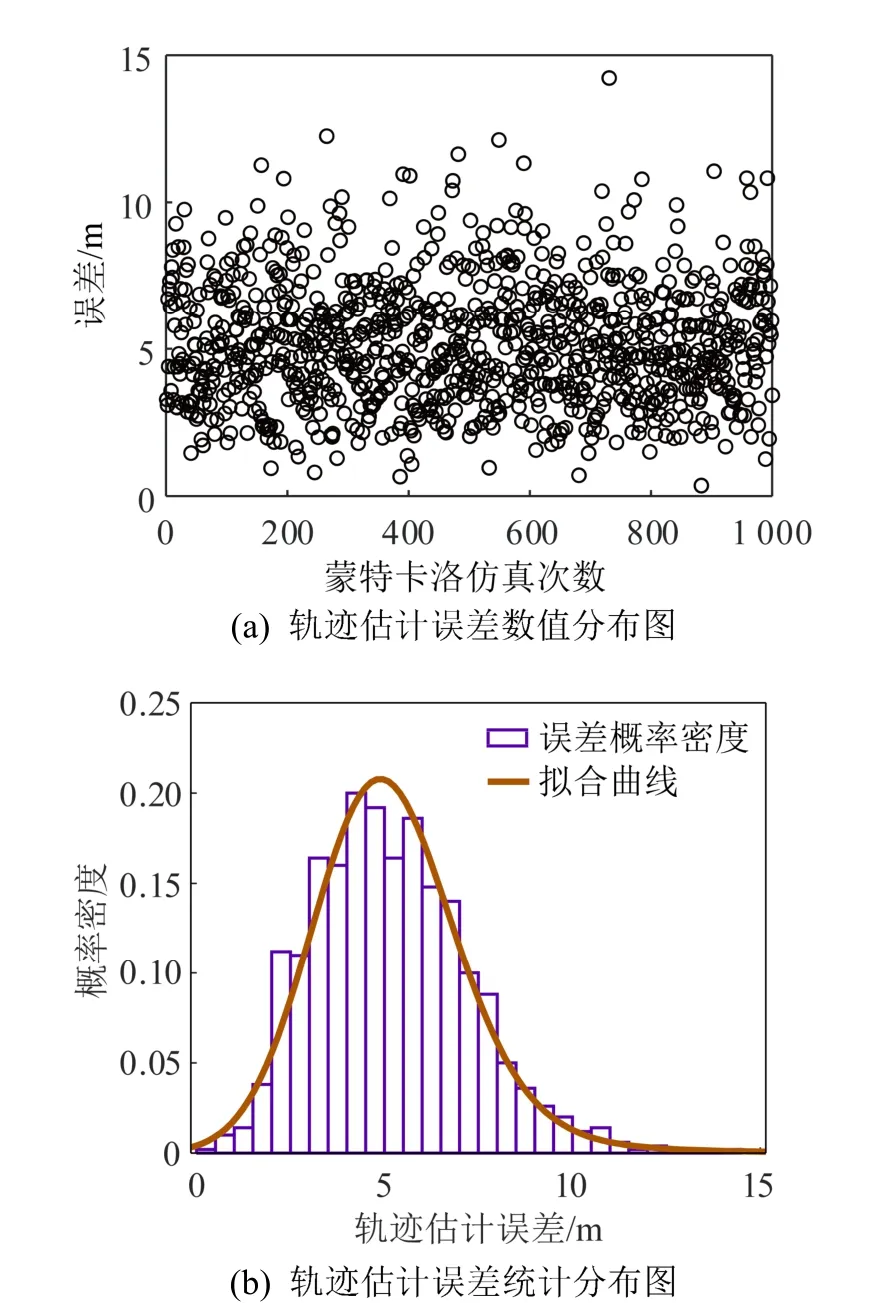
图13 波达方位估计随机误差在[-7°,7°]对轨迹估计影响 Fig.13 Influence of the random error of DOA estimation on the trajectory estimation in [-7°,7°]
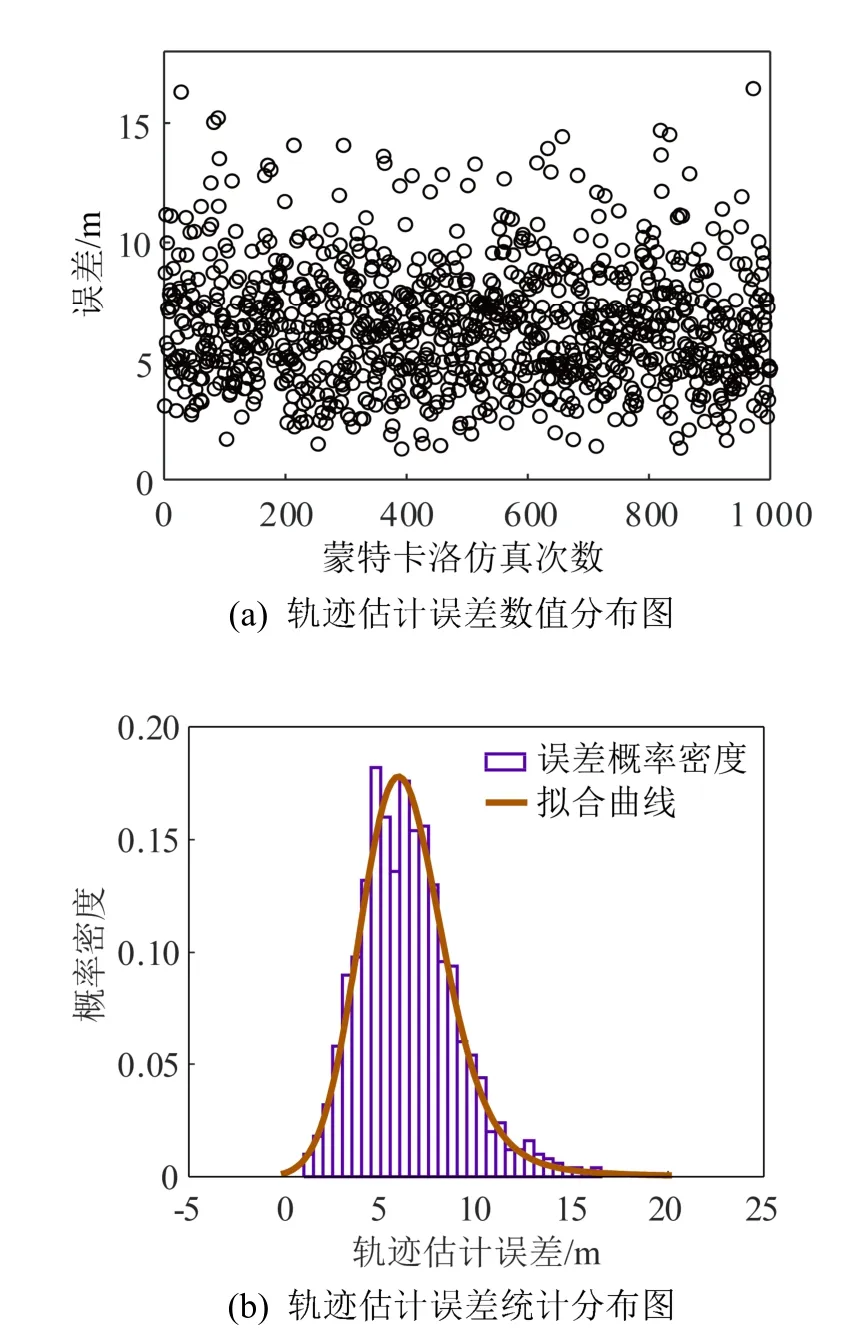
图14 波达方位估计随机误差在[-9°,9°]对轨迹估计影响 Fig.14 Influence of the random error of DOA estimation on the trajectory estimation in [-9°,9°]
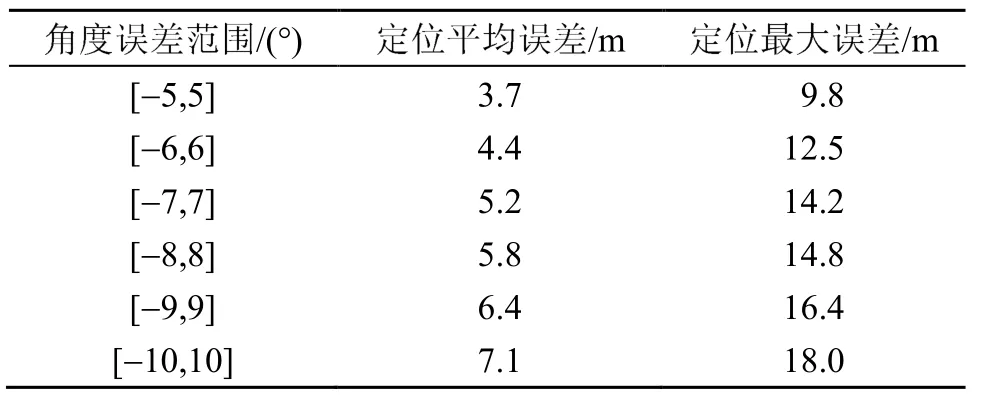
表2 1 000次蒙特卡洛仿真中轨迹估计的平均误差与最大误差 Table 2 Average error and maximum error of trajectory esti-mation in 1 000 times of Monte Carlo simulations
4 结论
本文针对高速飞行目标计算波达方位时由于目标高速运动,不同阵列所接收到的信号并非声源在同一时刻所发出,难以在时间维度上进行对齐等问题,不可避免存在误差。借鉴点云数据处理的思想,提出了一种基于空间匹配的高速飞行目标轨迹估计方法。对于单个阵列而言,对每一帧数据计算得到的波达方向在字典上进行匹配,找到误差最小的N个空间点进行直线拟合。再对两帧以上的数据所拟合的直线进行空间点采样,得到空间点数据集,通过空间平面拟合,得到估计平面。两个阵列解算得到的平面相交,相交直线即为高速飞行目标的轨迹估计结果。仿真结果表明:
(1)由于空间点直线拟合与平面拟合存在误差,造成轨迹估计结果存在误差。当阵列使用的数据帧数增加时,轨迹估计的误差减小。
(2)该算法可以减小单次波达方向估计误差对轨迹估计的影响。单阵列与双阵列的阵列安装误差造成的轨迹估计误差随飞行高度的降低而减小。目标飞行高度为120.9 m 时,单阵列与双阵列的阵列安装误差范围为[− 2 °,2 °],轨迹估计误差小于10 m。对于随机误差,该算法表现出了较好的鲁棒性。
仿真结果验证了高速飞行目标的轨迹估计算法的有效性。
