平衡衔铁受话器仿真分析方法研究进展

陆 晓，温周斌，李俊宝

（1.中国科学院声学研究所，北京 100190；2.中国科学院大学，北京 100049；3.浙江中科电声研发中心，浙江嘉善 314115；4.中国科学院声学研究所东海研究站，上海 201815）

0 引言

大部分受话器是动圈（电动）式受话器，而平衡衔铁受话器（Balanced Armature Receiver,BAR）则是一种比较特殊的受话器。相比于动圈式受话器，BAR 具有体积小、声压级高、失真小和电声转换效率高等特点[1-5]，特别适合于声品质要求高而体积又要求小的助听设备、入耳式耳机和各种军用头戴式耳机等产品。近年来，真无线立体声（True Wireless Stereo,TWS）耳机市场快速增长，BAR 有着更广泛的应有前景。

随着计算机技术的发展，仿真分析方法已经越来越多地用于电声换能器设计中。对于动圈式驱动的换能器单元及系统，它们的电磁场、振动系统和声场以及多物理场耦合仿真分析及辅助设计方法都已经比较成熟[6-10]，这些方法可有效提升产品研发的效率和速度，提高产品的质量和档次。

近十年来，国内外开展了不少BAR 仿真分析方法的研究工作。本文简要介绍了BAR 的工作原理，详细讨论了BAR 仿真分析方法研究进展，涉及集总参数模型、有限元、边界元和传输矩阵等主要研究方法，重点关注它的非线性、声场和失真等主要特性，并提出进一步研究的重点和对未来发展的展望。

1 平衡衔铁受话器（BAR）的工作原理

BAR 的体积较小，一般只有15～200 mm3。图1 给出了一款BAR 的半剖图[11]，由图可知，BAR由永磁体、磁轭、平衡衔铁、线圈、传动杆、振膜、外壳、上盖和出声孔等组成，平衡衔铁是其中最关键的部件。

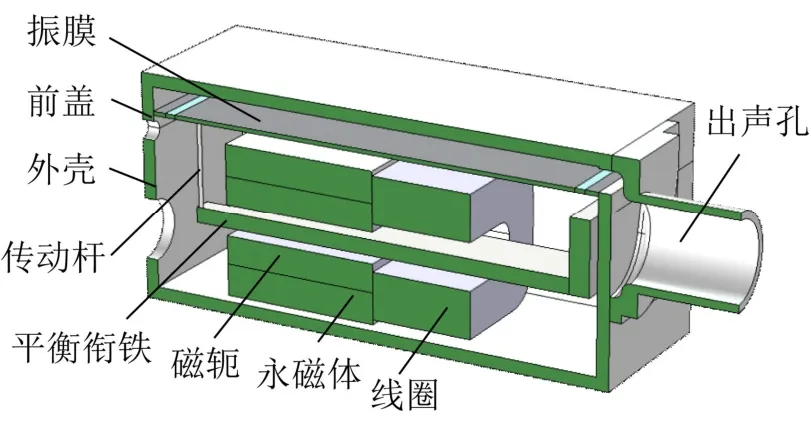
图1 BAR 的半剖几何模型[11] Fig.1 Section model of BAR[11]

BAR 的线圈和平衡衔铁的设计比较特殊。线圈环绕着平衡衔铁，但它并不与平衡衔铁接触，也不会随着平衡衔铁一起振动。所以，BAR 的有效振动质量不包括线圈，改变线圈匝数不会增加有效振动质量及降低高频声压级。当线圈中没有加载电流时，处于磁隙中的平衡衔铁受到两个大小相等、方向相反的磁吸引力，因此，平衡衔铁会被稳定在两块永磁体之间的某个平衡位置。实际上这两个相反的磁力并不绝对相等，但平衡衔铁因其自身的机械刚度会产生一个回复力，因而平衡衔铁不会大幅度偏离平衡位置，更不会贴到任何一块永磁体上[12]。

图2 给出了一个简化的BAR 磁回路[12-13]。在BAR 工作时，平衡衔铁会上下运动，而线圈是固定不动的。当给线圈加载电流时，线圈会将它所环绕的平衡衔铁磁化。当电流为正向时，则会增加上磁隙的磁通，使得磁隙中的平衡衔铁上表面和永磁体之间的吸引力增加；与此同时，下磁隙中的磁通减小，使得磁隙中的平衡衔铁下表面和永磁体之间的吸引力减小；平衡衔铁上表面所受到的力大于下表面所受到的力，就会使得平衡衔铁向上运动。同理，当电流为负向时，就会使得平衡衔铁向下运动。这样，随着电流方向的正负改变，平衡衔铁就会在磁隙中上下运动。因为平衡衔铁自身不是一个有效的声波辐射体，所以平衡衔铁通过一根传动杆刚性连接一块既薄又轻的振膜，而这块振膜又将整个受话器腔体分割为前腔和后腔，由振膜振动带动前后腔气体压缩或膨胀，从而产生声波，声波再由出声孔向外辐射。

图2 简化的BAR 磁回路[12-13]Fig.2 Simplified magnetic circuit of BAR[12-13]

2 非线性特性仿真分析

BAR 的平衡衔铁是导磁材料，它在磁场中空间位置的变化会影响电磁特性[12]。也就是说，BAR 的电磁特性会随着平衡衔铁的上下运动而改变，因而具有非线性特性。

BAR 的非线性会严重影响到它的声压级和失真，研究它的非线性非常重要。多位学者分别采用集总参数模型（Lumped Parameter Model,LPM）和有限元法（Finite Element method,FEM）研究了BAR 的非线性特性。

2.1 集总参数模型（LPM）

在采用集总参数模型分析问题时，假设了模型中的各个变量与空间位置无关，并认为各个变量的运动状态是均匀的，因而将这些参数简化为集总量。集总参数模型常用等效电路表示[14]，特别适用于设计理念的快速验证和参数优化[15]。LPM 求解的一般是代数方程或者常微分方程，因此模型求解效率较高，计算速度也较快。

Jensen 创建了BAR 磁场的集总参数模型[12-13]，将永磁体的磁动力和线圈的磁动力等效为电压，将上下磁隙的磁通量和平衡衔铁中的磁通量等效为电流，将永磁体磁阻和磁隙磁阻等其他材料磁阻等效为电阻[16]。图3 给出了与图2 磁回路相对应的等效电路图。在该等效电路中，FM是永磁体的磁动力，FMi是线圈的磁动力，Φg1和Φg2是上下磁隙的磁通 量，ΦA是平衡衔铁中的磁通量，RM是永磁体磁阻，Rg1和Rg2是磁隙磁阻。利用克希霍夫定律可得到上下磁隙的磁通量和平衡衔铁中的磁通量。再利用虚功原理[17]，进一步推导可得到平衡衔铁上的驱动力和线圈中的反电动势。

图3 磁回路等效电路[13]Fig.3 Equivalent circuit of magnetic circuit[13]

平衡衔铁上驱动力F(x,i)由加载电流i所引起的感生磁场力项、平衡衔铁位移x所引起的动生磁 场力项和失真项组成，而线圈中反电动势Uback则由电流变化引起项、位移变化引起项和失真项组成。F(x,i)及Uback的表达式分别为[12-13]

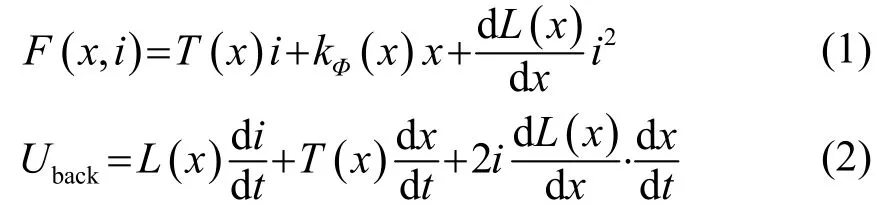
式中：T(x)是传递系数；kΦ(x)是刚度补偿系数；L(x)是电感，均为位移x的函数，都是非线性参数。T(x)、kΦ(x)和L(x)等可类比为动圈式受话器的“T/S”参数，都是BAR 重要的非线性参数。

与BAR 整个后腔的体积相比，振膜振动带来的后腔体积变化显著。即使振膜在小振幅范围内振动，后腔体积变化所引起的压强差也是不可忽略的。该压强差会影响BAR 振动系统的刚度，进而影响声压级[12-13]。该压强差所对应的表面作用力与平衡衔铁位移的比值被称为声刚度，它是位移x的函数，也是BAR 的重要非线性参数之一[18]。

2.2 改进的集总参数模型

多位研究者对Jensen 的集总参数模型做了改进，所改进的方向主要分为完善材料模型和考虑平衡衔铁位置的影响两个方面。

平衡衔铁和其他软磁材料的磁阻不是常数，当磁通密度改变时，磁阻也会随之变化。因此，需要建立它们的非线性材料模型，用更接近实际的B-H曲线而非常数值来定义磁特性，以提高模型精度。这里，B表示磁通密度，H表示磁场强度[18-22]。图4给出了一种平衡衔铁材料（PB）和一种磁轭材料（FeNi50）的B-H曲线，由图可知，它们的磁通密度B与磁场强度H的关系是非线性的，当磁场强度增加到一定程度之后，磁通密度会趋于饱和。建立非线性材料模型后，所需求解的方程则变为非线性方程。Xu 等[19-21]采用向后松弛牛顿迭代（under-relaxed Newton Raphson）的方法来求解该非线性方程。先假定初始的磁导率，可计算得到磁通量和磁通密度；又通过磁通密度可计算得到新的磁导率；再根据磁导率的差值来决定是否需要继续迭代。Ziolkowski[22]则采用（反正切）函数来拟合平衡衔铁的B-H 曲线，并用一个函数表示出平衡衔铁中磁通量和磁势之间的关系，将该函数代入到磁势平衡的方程式中，最后通过数值求解可得到平衡衔铁中的磁场强度。Klippel[23]建立了非线性方程，指出在获得电信号和位移的前提下，可以通过不断拟合的方法最终得到非线性参数。

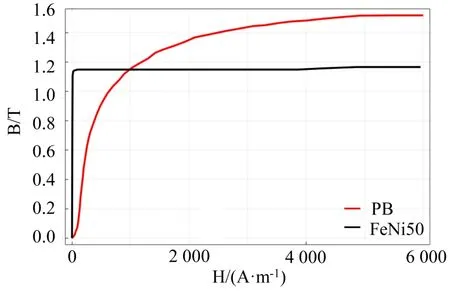
图4 软磁材料磁特性：B-H 曲线[18]（PB 材料用于平衡衔铁，FeNi50 用于磁轭）Fig.4 Magnetic property of soft magnetic material:B-H curves (PB for armature and FeNi50 for magnet housing)[18]

由于BAR 的尺寸非常小，在它的装配过程中时常会出现平衡衔铁没有正确安装在磁隙中间位置的情况。当平衡衔铁不处在磁隙中间位置时，上下磁隙间距是不相同的，因而上下磁隙的磁阻也是不相同的。Tsai[24]、Ziolkowski[22]和Klippel[23]都根据平衡衔铁的实际位置，修改了上下磁隙的磁阻，建立了改进的集总参数模型，得到了新的非线性参数。

平衡衔铁的材料非线性和平衡衔铁在磁隙中的位置都会影响BAR 的非线性特性。Xu 等[19-21]的研究涉及了平衡衔铁的材料非线性，Tsai[24]的研究涉及了平衡衔铁在磁隙中的位置，而Ziolkowski[22]和 Klippel[23]的研究虽然均有涉及，但是Ziolkowski[22]仅研究了不同大小加载电流时的平衡衔铁位移，没有给出非线性参数随位移的变化，而Klippel[23]不仅给出了非线性参数的表达式，他还指出，若经过合理设计，可以利用材料非线性来抵消平衡衔铁位置对BAR 特性的不利影响。

2.3 有限元法（FEM）

有限元法（FEM）是一种通用的解偏微分方程的方法，使用积分方法代替偏微分方程来建立系统的代数方程组[25]。利用有限元法，可以快速比对分析不同几何尺寸或不同材料参数对结果的影响，常用于研究涉及多物理场耦合的问题[26]。求解有限元模型的计算效率受网格数量、求解器和物理场等因素的影响较大[27]。

在采用有限元法分析时，准确输入几何模型和材料模型是非常重要的。Xu 等[28-29]认为非线性特性主要涉及BAR 的磁路系统，因而所建立的几何模型忽略了振膜、传动杆、外壳、上盖和出声孔等部件，仅包含永磁体、磁轭和平衡衔铁等。而在Jensen所建立的几何模型中，由于不需要加载电流或电压，因而进一步忽略了线圈，只包含了相对磁导率大于1 的导磁材料[12-13]。对于材料模型，假设永磁体是各向同性的，通过剩磁和相对磁导率建立其材料模型，通过常数值的相对磁导率或者更接近实际的B-H 曲线建立导磁材料的材料模型。但文献[12-13,28-29]中均未研究磁性材料磁滞的影响。

Xu 等[28-29]对模型进行了瞬态分析，他们认为需要计算足够多的周期才能确保磁场震荡达到稳定状态。根据频率高低划分不同疏密的网格，计算不同数量的周期以提高计算效率。在涡电流积聚的导电材料边界上加密网格，可模拟涡电流的趋肤效应。相对稳态和频域等其他求解方式，瞬态求解效率较低，且容易出现不收敛的问题。而Jensen 仅对磁场进行了稳态分析[13]。因为模型中没有包含力学分析，因而一端固定的平衡衔铁不会因受力而产生弯曲变形，但Jensen 通过平移平衡衔铁位置（而非弯曲）的方式近似模拟了它产生的弯曲变形。因此，仿真结果可能与实际相比有较大误差。

通过上述有限元分析，可以得到磁通密度分布等数值仿真分析结果。通过计算麦克斯韦应力张量，可以得到平衡衔铁上的电磁力密度，再对平衡衔铁表面上的电磁力密度做积分，可得到平衡衔铁的驱动力。由于Xu 等[28-29]和Jensen[13]对模型分别采用了瞬态和稳态两种不同的分析方式，所以对分析结果的后处理方式也略有不同。Xu 等分别计算了线圈加载电流和不加载电流两种情况下的平衡衔铁上驱动力，前者称为总力，而后者称为动生磁场力。将这两个力相减，可得到由加载电流所引起的感生磁场力，而感生磁场力与位移的比值又被定义为力因子（Force Factor）。对线圈截面积的磁通量做积分，可得到线圈中的磁通量，由单位电流的磁通量变化可得到电感（Inductance），而由单位位移的磁通量变化可得到“速度（Speedance）”。Jensen 则通过稳态分析得到不同位移时的驱动力，力与位移的比值即为刚度补偿系数[13]。

3 声压级仿真分析

采用集总参数模型和有限元法，可以仿真分析得到BAR 的声压级。为了提升仿真分析的精度和效率，研究者们还提出了集总参数模型与有限元法相结合、传输矩阵和模态叠加法等多种分析方法。

3.1 集总参数模型

利用2.1 节所述集总参数模型，可以得到平衡衔铁位移及速度的时间函数，再利用快速傅里叶变换（Fast Fourier Transform,FFT）可得到平衡衔铁位移频谱。假设声场中的振动传递是线性的，基于圆形活塞辐射原理[14]，利用振膜的速度可计算得到声压和声压级[24]。

3.2 有限元法

Xu 提出的声压级仿真分析方法[19]先采用了有限元法仿真分析包含涡电流的电磁场瞬态特性，在得到动生磁场力等非线性参数之后，再采用有限元法，将振动系统和声场耦合在一起进行频域分析，得到力与位移或者力与声压的传递函数。然后，将得到的结果进行数值计算，利用电压方程求解得到电流和位移，通过迭代得到实际的电流、驱动力、位移和声压的时间函数[30]；最后，通过傅里叶变换最终可得到位移、阻抗、声压级和失真的频域响应。图5 是声压级仿真分析法的流程。

图5 分析流程[19] Fig.5 Flowchart of analysis procedures[19]

文献[31]提出了一种分步进行的BAR 的有限元数值仿真方法。它首先对BAR 的磁场特性进行稳态分析，计算得到可随平衡衔铁运动而变化的磁场力和反电动势；然后，建立电磁场、结构和声场耦合分析模型，并利用前面稳态求解得到的可随平衡衔铁运动而变化的磁场力和反电动势，再进行频域分析，最终计算得到BAR 的声压级和阻抗曲线。图6 给出的是声压级曲线的仿真结果和测量结果。

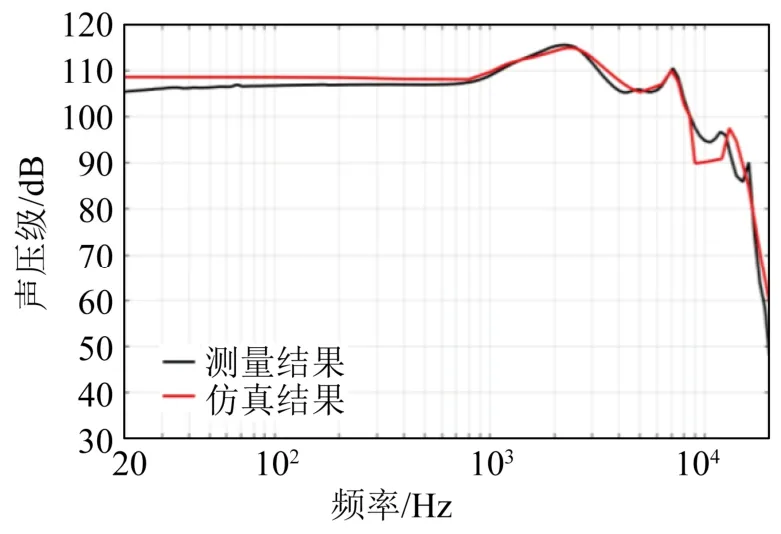
图6 声压级曲线的仿真结果和测量结果 Fig.6 Simulation and measurement results of SPL

3.3 集总参数模型与有限元法相结合

集总参数模型具有简单和高效的特点，但是模型进行了简化甚至忽略了很多因素，只专注了一些关键的因素。对于复杂结构、中高频分割振动、宽频带范围和多模态等情形，集总参数模型的仿真分 析精度不高[31]。而采用有限元方法可分析较为复杂的模型和分布式参数系统，精度较高，但往往计算效率不高。

采用集总参数模型与有限元相结合的方法来仿真分析BAR 的声压级，可充分利用这两种方法的优点，达到同时提高仿真分析精度和效率的目的。Sun 等以一个简化的BAR 为研究对象，提出了一种集总参数模型与有限元相结合的声压级仿真分析方法[15]，图7 给出了该方法所对应的仿真模型。在该模型中，采用有限元分析振动系统，采用集总参数模型分析声场。利用振膜实现振动系统和声场的双向耦合，一方面，对振膜表面上分布的振动速度进行积分，可得到体积速度，它体现了振动系统对声场的作用；另一方面，对振膜表面上前后腔的声压进行积分，可得到作用力，它体现了声场对振动系统的反作用。

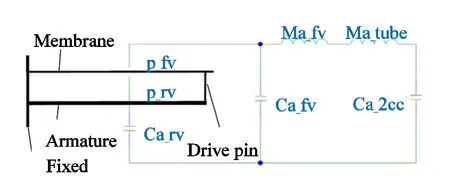
图7 用于简化的BAR 的FEM-LPM 模型[15] Fig.7 Integrated FEM-LPM model for simplified BAR[15]

为进一步提升计算效率，文献[32-33]还提出了 一种BAR 声压级的集总单元（Lumped Element,LE）多模态模型，图8 给出了该模型的等效电路[32-33]。其建模思路是：首先在有限元方法的辅助下，利用模态分解技术，将BAR 多自由度振动系统解耦为多组单自由振动系统；再基于能量准则实施模态截断，选择出四个起主导作用的模态，并计算这几个主导的模态对应的等效刚度、阻尼系数、重量和加载力等；最后将这四个模态的单自由度振动系统分别与声场耦合，从而建立多模态模型。

图8 BAR LE 多模态模型的等效电路[30-31]Fig.8 Equivalent circuit of LE multimode model for BAR[30-31]

Sun 等[32]所提出的两种模型均显著提高了求解效率，但是模型中没有包含磁路。在仿真分析BAR声压级时，还应分析磁路对振动系统的作用和影响。对于涉及多物理场的耦合分析问题，更需要采用集总参数模型与有限元相结合的方法来提高计算效率。Gary 在原来电力声等效电路中，将简化的等效电路更改为有限元声振模型，利用COMSOL建模，将耦合了电磁场的集总参数模型，与振动系统和声场的有限元分析相结合在一起进行仿真计算[34]。Bai 等则在集总参数模型中混合了有限元方法来预测声压级的高频响应[35]。基于COMSOL 软件，Bai 等采用有限元方法对振动系统进行谐波分析，计算得到机械阻抗。这个机械阻抗是一个随频率变化的传递函数，用它替换原等效电路模型中振动系统质量、刚度和阻尼等电路元件，可更加准确地体现总驱动力在高频段与振膜所有节点的平均速度之间的关系。Bai 等给出了混合方法的有效性，如图9 所示，集总参数模型对应的仿真结果与测量结果误差较大，而当采用集总参数模型和有限元混合的方法后，仿真结果准确体现了中高频的峰谷特征。但是，对磁路采用集总参数模型来分析，会产生因简化而引起的误差，无法分析一些重要因素的影响。

图9 BAR 轴向SPL 响应的仿真结果和测量结果[34]Fig.9 Comparison of the simulated and measured on-axis SPL responses of the BAR[34]

3.4 模态叠加法等

对于一般以力作为输入的结构响应问题，可以采用完全法或者模态叠加法进行求解。对于自由度 多、计算频点多的频率响应问题，完全法可能需要数小时甚至数天时间才能完成计算，而模态叠加法往往可以在几分钟就完成计算。只要选取的模态阶数合适，采用模态叠加法也可获得足够高的计算精度[36]。

Jiang 在采用数值仿真方法计算BAR 的声压级时，对于振动系统和声场耦合的频域分析模型，他采用了模态叠加法来提高求解的计算效率[35]。因为BAR 的动生磁场力会将平衡衔铁拉离平衡位置，它的影响近似于一个负刚度。所以，Jiang 在对振动系统进行模态分析时，适当调整了平衡衔铁的杨氏模量，使得调整杨氏模量后的平衡衔铁机械刚度等效于振动系统总刚度，该总刚度考虑了动生磁场力的影响。在得到固有频率和模态等模态分析结果之后，再进行基于模态叠加的振动系统和声场耦合分析。

Xu 在进行BAR 振动系统和声场的耦合分析时，为了提高计算效率，还采用了边界元法（Boundary Element Method,BEM）来分析声场[19]。边界元法是另一种数值仿真分析方法，它以定义在边界上的边界积分方程为控制方程，偏微分方程可转换为只包含边界积分的积分方程，这样，三维问题可简化为二维问题[1]。

为提高仿真模型的求解计算效率，在文献[31]中提出的声压级数值仿真分析方法中，采用了特定的阻抗边界条件替代711 耦合器的简化方法。因为BAR 是在压力场环境下使用的，它的声输出一般需要配合711 耦合器。采用简化方法后，在仿真模型中不需要建立耦合器声腔模型，只需要包含BAR和小部分声腔，从而可以大幅降低计算量。

3.5 传输矩阵

传输矩阵又称为转换矩阵、T 矩阵和ABCD 矩阵，可用来评估任意复杂度的级联单元形成的系统的特性，整个级联系统的矩阵是每个级联单元矩阵的乘积[37]。

David 认为传输矩阵是一种分析和设计BAR的简单且精确的方法，利用该方法可以比较方便地、模块化地拆分和计算复杂系统，避免直接求解复杂系统的联立方程[38]。Jiang 等在计算BAR 声压级时，将从出声孔到压力场耦合腔之前的声波传递过程分成多个声管道，用传输矩阵来表示每个声管道的声压输入和体积速度输出关系[39]。Kim 通过传输矩阵研究了BAR，最终建立了如图10 所示的电路模型[40-42]。为了计算声压级，电学和力学部分通过转换器（Gyrator,GYR）耦合，对角线上的系数必须是相反数，这是所有电声换能器的必要条件。力学和声学部分则通过转换器（Transfer,TRF）耦合。

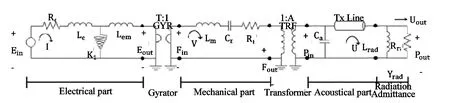
图10 BAR 最终的电路模型[42]Fig.10 Final circuit model of BAR[42]

4 失真仿真分析

失真是另一个重要特性，多位研究者采用非线性时域模型研究了BAR 的失真特性。对于非线性时域模型，模型求解方法非常重要。

4.1 非线性时域模型

Jensen 在其研究BAR 非线性特性的集总参数模型的基础上，创建了研究失真特性的非线性时域模型，其所对应的控制方程为[13]

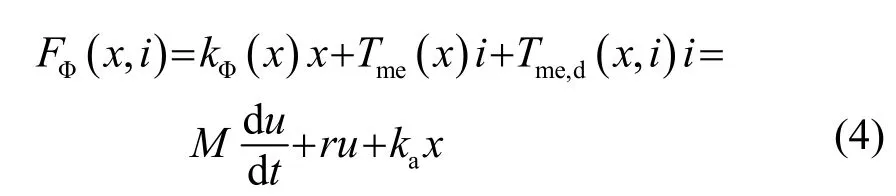
式中：Ein是加载电压，RL是线圈直流电阻，Uback是反电动势，FΦ(x,i)是平衡衔铁所受驱动力，M是振动系统的重量，u是速度，r是系统阻尼，ka是结构刚度。

由于制造工艺的影响，BAR 上下磁隙的磁通往往不对称，而导致磁通不对称的主要原因是磁隙截面积不同和磁隙间距不同。Tsai 等[24]提出，可根据实际的磁隙截面积和磁隙间距重新定义磁隙磁阻、线圈磁动力和永磁体的磁动力，并将它们代入到Jensen 创建的非线性时域模型中，得到了新的非线性时域模型。Tsai 等采用该方法改进了一款BAR的设计，图11 给出了原设计和改进后的测量结果和仿真结果[24]，由图可看出，改进后的BAR 偶次谐波失真明显减小，仿真结果和测量结果基本一致。

图11 BAR 原设计和改进后的非线性谐波失真[24] Fig.11 Comparisons of the nonlinear harmonic distortion between the original BAR design and improve one[24]

Klippel[23]则进一步改进了非线性时域模型，如图12 所示。基于这个改进的模型，不仅可以研究软磁材料的饱和等对失真的影响，还可以分析平衡衔铁振动平衡位置与静态位置的偏置所导致的非线性参数不对称与失真的关联关系。

图12 由平衡位置xe考虑位移ξ 的BAR 扩展模型的 等效电路图[13]Fig.12 Equivalent circuit of the extended BAR model considering the displacement ξ from the equilibrium position xe [13]

4.2 模型求解

对于非线性时域模型，需要求解的是非线性的传递方程，Jensen 采用了较为简单的向前欧拉（Forward-Euler）方法[12-13]，也可以采用龙格-库塔（Runge-Kutta）方法。Tsai 采用了混合样条差分（Hybrid spline difference method）方法，该方法能获得连续函数的二阶小量，其精度高达O（∆t4）[24]。求解非线性模型可以得到基频响应、平衡衔铁的位移、最大输出（例如最大声压级）、奇次和偶次谐波失真以及互调失真等特性[23]。

因为失真涉及非线性，建模和求解失真模型都非常困难，所以至今很少有人基于有限元法研究BAR 的失真。

5 结论

BAR 因其具有独特的优势和广泛的应用前景而受到持续的广泛关注和深入研究。本文在简要介绍BAR 的工作原理之后，详细介绍了近10 年来国内外仿真分析方法研究进展，重点关注了它的非线性、声压级和失真等主要特性。

相较于动圈式驱动的电声换能器，BAR 的线圈和平衡衔铁的设计比较特殊。当BAR 工作时，线圈是不动的，而平衡衔铁是运动的。BAR 的独特设计使得它具有非凡的优势，平衡衔铁的运动也使得它的电磁特性具有特别的非线性特性。多位研究人员分别采用了集总参数模型和有限元法研究了BAR 的非线性特性，作者认为在深入开展理论研究的基础上，有必要开展非线性特性的仿真研究和实验研究。

为了高效且准确地仿真分析BAR 的声压级，研究人员采用了集总参数模型与有限元法相结合、模态叠加法、边界元法和传输矩阵等多种方法，取得了不俗的研究成果，但只有少数几位研究人员在仿真声压级时考虑了它的非线性。作者认为如何在线性分析中充分考虑非线性的影响，且保证整个仿真分析过程是高效的，是一个重要的研究方向。

失真分析是仿真分析中的重点和难点，几位研究者基于非线性时域模型研究了BAR 的失真特性，并选用了不同的模型求解方法以获得更快、更好的仿真结果。但基于集总参数模型的非线性时域模型无法准确分析振膜分割振动等的影响。

未来可以就以下方向进行进一步研究：（1）研究磁性材料的非线性、磁滞损耗和磁饱和等，建立更准确的材料模型；（2）研究传递系数、补偿刚度、电感和后腔声刚度等非线性参数，更精确地仿真计算声压级和失真；（3）客观评估BAR 的电声转换效率、最大声输出和稳定性等指标，探寻BAR 高效、准确的仿真设计方法。