调频初相位补偿的广义Warblet 变换时频分析

张 地，周士弘，戚聿波，杜淑媛

（1.中国科学院声学研究所，声场声信息国家重点实验室，北京 100190；2.中国科学院大学，北京 100049）

0 引言

时频分析能够体现被分析信号的时间-频率二维能量分布，是常用的准稳态信号处理方法。时频分析方法主要有两类：不需要信号先验知识的非参数化方法和需要已知信号先验知识的参数化方法。非参数化方法包含短时傅里叶变换（Short Time Fourier Transform,STFT）、Wigner-Vile 分布（Wigner-Vile Distribution,WVD）和连续小波变换（Continuous Wavelet Transform,CWT）及其改进算法等。STFT方法将信号划分为若干重叠或不重叠的小段并对每一小段信号加窗后做傅里叶变换，性能由所选取的时间窗决定，若时间窗较长则频率分辨率高但时间分辨率低，反之则时间分辨率高但频率分辨率低。Kwok 等[1]提出了自适应STFT（Adaptive STFT,ASTFT）方法，利用最大似然准则在不同时间选用不同的时间窗，进而得到最高的时频输出峰值。WVD方法对各段信号自相关函数做傅里叶变换，调频信号自相关能够得到比信号与傅里叶基函数相关输出更大的模值，但自相关操作会引入交叉项，对瞬时频率估计带来很大影响。吕军等[2]提出了一种改进的STFT-WVD 方法，利用在STFT 输出中不存在WVD 输出交叉项的特性，将两种时频分析输出矩阵对应位置处元素相乘并设定合适的阈值进行后续分析。CWT 方法通过改变时频分辨尺度提高分析性能，在低频段具有更高的频率分辨率，在高频段则具有更高的时间分辨率[3]。与STFT 类似，CWT性能与被分析信号和选取的母小波有关。

参数化方法可利用广义时频变换（General Parameterized Time-Frequency Transform,GPTF）[4]框架统一描述，包含多项式Chirplet 变换（Polynomial Chirplet Transform,PCT）[5]、多普勒Chirplet 变换（Doppler Chirplet Transform,DCT）[6]、样条基Chirplet 变换（Spline-Kernelled Chirplet Transform,SCT）[7]、广 义 Warblet 变换（Generalized Warblet Transform,GWT）[8-9]等。这些方法从不同角度描述信号时频走势，PCT、SCT 和GWT 分别采用多项式、三次样条插值函数和三角函数描述信号的时频走势；DCT 则直接解算信号源与接收点间径向运动引起的多普勒频移关系得到瞬时频率表达式。GPTF 的核心思想是利用旋转算子抵消信号相位中除频率一次项之外的部分，在时频图上体现为将时变线谱旋转为时不变线谱，然后利用平移算子修正旋转算子带来的频率偏移，再利用单频信号作为核函数对算子作用后的信号做傅里叶变换，此时每个时间分析窗内信号频率均不随时间变化，能够与傅里叶基函数完全匹配，使能量集中在某一频点，从而获得更高的时频能量聚集度，更有利于线谱检测和瞬时频率估计。PCT 和DCT 方法适用于频率非周期变化信号，在处理频率周期变化信号方面存在局限性；SCT 方法虽能处理频率周期变化信号，但算法涉及到的样条基函数较复杂；GWT 方法利用三角函数描述信号瞬时频率，算法较易实现且对频率周期变化和非周期变化类信号均有较好的处理效果。传统的Warblet 变换（Warblet Transform,WT）[9]方法在每一个时间窗内确定调频相位，算法较难实现。GWT 在此基础上，利用旋转算子和平移算子对信号整体操作后再进行STFT，算法更易实现。GWT 方法采用三角函数描述信号瞬时频率，适用于瞬时频率随时间近似呈三角函数变化的信号，例如微多普勒雷达信号[10]以及频率周期变化的水声信号[11]。Zhou 等[12]提出修正的广义参数化时频分析（Modified Generalized Parameterized Time-Frequency,MGPTF）方法和相干单程多普勒干涉 MGPTF（Coherent Single Range Doppler Interferometry-MGPTF,CSRDI-MGPTF）方法，MGPTF 利用三角函数描述信号瞬时频率并在GWT 基础上增加了一层关于调制成分个数的循环，使得瞬时频率的估计更为准确；CSRDI-MGPTF 方法能够适用时频轨迹部分中断的情况。王晓[13]利用时域平移校正法对瞬时频率傅里叶变换结果进行校正，提高时频轨迹参数的估计精度，进而提高瞬时频率估计精度。

现有算法在调制成分估计时均没有考虑时频输出起始时刻与信号起始时刻之间存在由1/2 个时间窗长度引起的相位差。对于频率时变信号，当时频分析所需时间窗较长时，如果不对调频初相位进行补偿则无法对调频成分进行准确估计，GWT 算法性能将下降甚至失效。本文提出一种调频初相位补偿的GWT（Frequency Modulation Initial Phase Compensation-GWT,FMIPC-GWT）方法，在长时间窗时频分析时依旧能够准确估计瞬时频率，对时变线谱检测和瞬时频率估计具有重要意义。

1 广义Warblet 变换

当信号频率随时间变化时，对整段信号做频谱分析无法体现信号频率随时间变化情况。通常假设信号在各小段时间内频率不发生变化，对各小段时间做频谱分析，再将所有结果表示为能量在时间-频率二维平面上的分布。然而频率时变信号的数学形式决定了在时频分析时间窗内，信号频率依旧是变化的，傅里叶变换输出无法将信号全部能量集中到某一频点上，造成时频能量聚集度下降、输出信噪比降低以及瞬时频率估计准确性下降。

GWT 算法的典型应用场景之一是处理正弦调频信号，信号模型为

其中：A0为信号幅度；f0为中心频率；m为调制成分序数；Fm和ψm分别为调制频率和调频初相位；ϕ0为载波初相位；Bm描述频率调制成分的强度，为方便后续推导，令，am为频率调频幅度。信号瞬时频率可以表示为

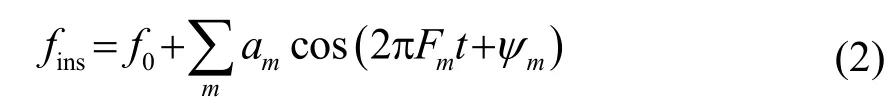
定义旋转算子φR和平移算子φS分别为

GWT 算法可以表示为[8]

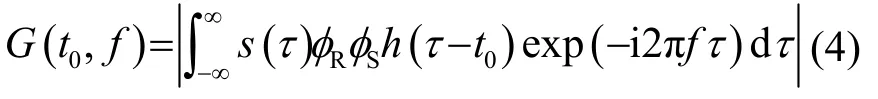
其中：t0为各时间窗中心时刻；h(t)为时间窗函数，常用时间窗函数有高斯窗、汉宁窗等。

由式（4）可以看出，旋转算子将信号相位项中时变部分抵消掉，使得信号频率不随时间变化，之后通过平移算子将各时间窗内的信号频率修正到原信号频率。与STFT 相比所不同的是经过旋转算子作用后，信号频率在每一个分析时间窗内都是恒定不变的，能够与傅里叶基函数exp (i 2πft)的共轭完全匹配，从而使得时频分析算法输出信噪比最大，提高了时变线谱的检测能力。

对于不是正弦调频信号的其他非线性调频信号，虽然其瞬时频率不再具有式（2）的形式，但依旧可以通过傅里叶变换将瞬时频率随时间变化的情况用若干三角函数的线性组合来表示。因此，GWT类方法依旧适用[4]。

2 调频初相位补偿的GWT 方法

GWT 法需利用瞬时频率轨迹估计调频参数。由于时频分析结果对应时刻为所选取的各时间窗对应的中心时刻，当时间窗较长时，调频初相位估计结果将出现较大偏差。FMIPC-GWT 方法对调频初相位估计结果进行修正，避免了调频参数估计结果与信号原有调频成分间的失配。同时FMIPC-GWT 瞬时频率估计结果可再次作为参数输入FMIPC-GWT 算法进行进一步的时频分析，经过多次迭代可进一步提高线谱瞬时频率估计准确性。

2.1 调频参数估计与初相位补偿

GWT 算法的核心思想是用一系列三角函数刻画信号瞬时频率，这需要对调频参数进行估计，确定各调制成分幅度am、调制频率Fm和调频初相位ψm。首先对信号进行φR=1、φS=1 的GWT，此时GWT 退化为STFT。瞬时频率的估计可表示为

其中：n为整数，∆f=1 (∆t⋅N)为离散频率间隔，∆t为各时间窗中心时刻的间隔，N为离散傅里叶变换点数。

傅里叶变换系数与傅里叶变换间关系为

其中：n0为各调制频率所在频域离散采样点序数。

需要注意的是，上述对信号调频参数的估计是建立在对信号时频分析结果的基础上，而时频分析输出时刻对应各时间窗的中心时刻，因此调频初相位估计实际上是对信号瞬时频率轨迹在第一个时间窗中心时刻处相位的估计。由于旋转算子和平移算子是作用到起始时刻为0 的整段信号上，因此式（9）中对调频初相位的估计与实际调频初相位之间存在由1/2 个时间窗长度所引入的相位差。因此，相位补偿后调频初相位估计可以表示为

需要指出的是，GWT 算法中将信号瞬时频率写作一系列余弦函数和正弦函数的线性组合[8]，可改写为式（2）带有初相位的余弦函数形式，但此处初相位依然是没有考虑1/2 个时间窗长所引入的相位。

2.2 迭代提升参数估计精度

利用STFT 结果估计调频参数后进行FMIPC-GWT 时频分析，可提高瞬时频率估计精度，并可利用FMIPC-GWT 结果进行调频参数估计，将估计结果作为参数再次输入FMIPC-GWT 算法做进一步的时频分析。多次迭代的FMIPC-GWT 的步骤为：

（1）对信号进行STFT，高斯时间窗长L、滑动长度为0.02L。在一定带宽内利用式（5）得到瞬时频率的估计。

（2）利用式（6）对瞬时频率估计结果进行傅里叶变换得到Fins，可以得到各调制成分的调制频率、调制幅度和调制频率初相位。

（3）将步骤（2）中得到的调频参数估计结果代入式（3）得到旋转算子φR和平移算子φS，并利用得到的算子对原信号进行FMIPC-GWT 时频分析。

（4）利用式（5）得到新的瞬时频率估计，并重复步骤（2）～（4）直到满足终止条件。

将STFT 作为算法第1 次迭代，两次瞬时频率估计相对差值为

3 仿真验证

3.1 算法仿真实现

设频率时变信号满足式（1）并包含2个频率调制成分，调制频率Fm分别为3 mHz 和9 mHz，调频幅度am均为0.3 Hz，调频初相位ψm分别为π/6和π/3，中心频率f0=30 Hz，A0=1，ϕ0=0，信号时长1 000 s。对信号添加谱级信噪比为−2 dB 的高斯白噪声，谱级信噪比定义为全带宽信噪比与工作带宽B的乘积，对数表示为[14]

其中：和RSN分别为谱级信噪比和全带宽信噪比的对数形式，，fs=250 Hz 为信号采样频率。

对信号进行STFT，高斯时间窗长 80 sL=，滑动长度1.6 s。如果不对调频初相位进行补偿，直接在STFT 基础上利用式（5）～（9）对信号进行GWT，迭代终止门限δ设为0.1%，最大迭代次数为5，算法因触发最大迭代次数约束条件而终止，其中STFT 作为第1 次迭代。每次迭代后利用瞬时频率轨迹进行调频参数估计，前3 次参数估计结果如表1 所示。表1 中，调频幅度和调制频率误差均为估计值与真值差值的绝对值与真实值的百分比，调频初相位误差为估计值与真值差值的绝对值与2π的百分比。误差保留小数点后1 位有效数字。调频参数估计结果，特别是调频初相位估计结果误差较大。利用表1 中调频参数估计的各次迭代结果恢复的瞬时频率与真实值以及瞬时频率提取值对比如图1 所示。图1 中黑色虚线为时频分析后利用式（5）提取到的瞬时频率轨迹（简称提取值），蓝色点划线为利用对瞬时频率轨迹进行参数估计到的调频参数恢复出的瞬时频率轨迹（简称恢复值），红色实线为瞬时频率真实值。由图1 可以看到红色实线与蓝色点划线之间存在较大误差，这主要由相位差引起，利用蓝色点划线所表示的参数进行下一步迭代便会造成算法性能下降甚至失效。GWT 算法前3 次迭代输出结果如图2（a）～2（c）所示，其中图2（a）为STFT 结果，第4～5 次迭代时频输出结果与第2～3次结果（图2（b）～2（c））类似（图略）。由于调频参数估计误差较大，图2（b）～2（c）中是许多杂乱的亮线，无法分辨出线谱，时频分析效果甚至不如STFT 方法。

表1 GWT 前3 次迭代调频参数估计结果 Table 1 Frequency modulation parameter estimation results for the first 3 iterations of the GWT method

图1 GWT 前3 次迭代瞬时频率恢复值、真实值及提取值对比 Fig.1 Comparison of the recovery,real and extracted values of the instantaneous frequency for the first 3 iterations of the GWT method

图2 仿真GWT 前3 次迭代结果 Fig.2 The simulation results for the first 3 iterations of the GWT method

利用第2 节中介绍的FMIPC-GWT 方法对信号进行时频分析，算法经过3 次迭代后终止，各次迭代的输出结果如图3（a）～3（c）所示。图3（a）为第1次迭代即STFT 方法输出结果，由于存在较强噪声且傅里叶分析基函数不能很好地匹配频率时变信号，导致信号时频轨迹存在许多断点，很难分辨出线谱所在位置。表2 为FMIPC-GWT 算法各次迭代调频参数估计值结果，可以看出对调频初相位进行补偿能够有效提高调频参数特别是调频初相位估计的准确性。利用相对准确的调频参数估计结果得到的旋转算子和平移算子对信号做 GWT 即FMIPC-GWT，第2～3 次迭代的输出结果如图3（b）～3（c）所示，第2 次迭代输出相较于STFT 结果有很大改善，能够比较清晰地看到信号瞬时频率轨迹，第3 次迭代输出结果进一步提升了瞬时频率轨迹的清晰程度。图4 为利用FMIPC-GWT 时频分析算法各次迭代调频参数估计值恢复出的瞬时频率轨迹与真实值和在时频图上提取的瞬时频率轨迹的对比，可以看到经过对调频初相位补偿后的调频参数能够很好地描述信号瞬时频率走势，经过迭代后瞬时频率提取值与真实值基本一致。

表2 FMIPC-GWT 前3 次迭代调频参数估计结果 Table 2 Frequency modulation parameter estimation results for the first 3 iterations of the FMIPC-GWT method

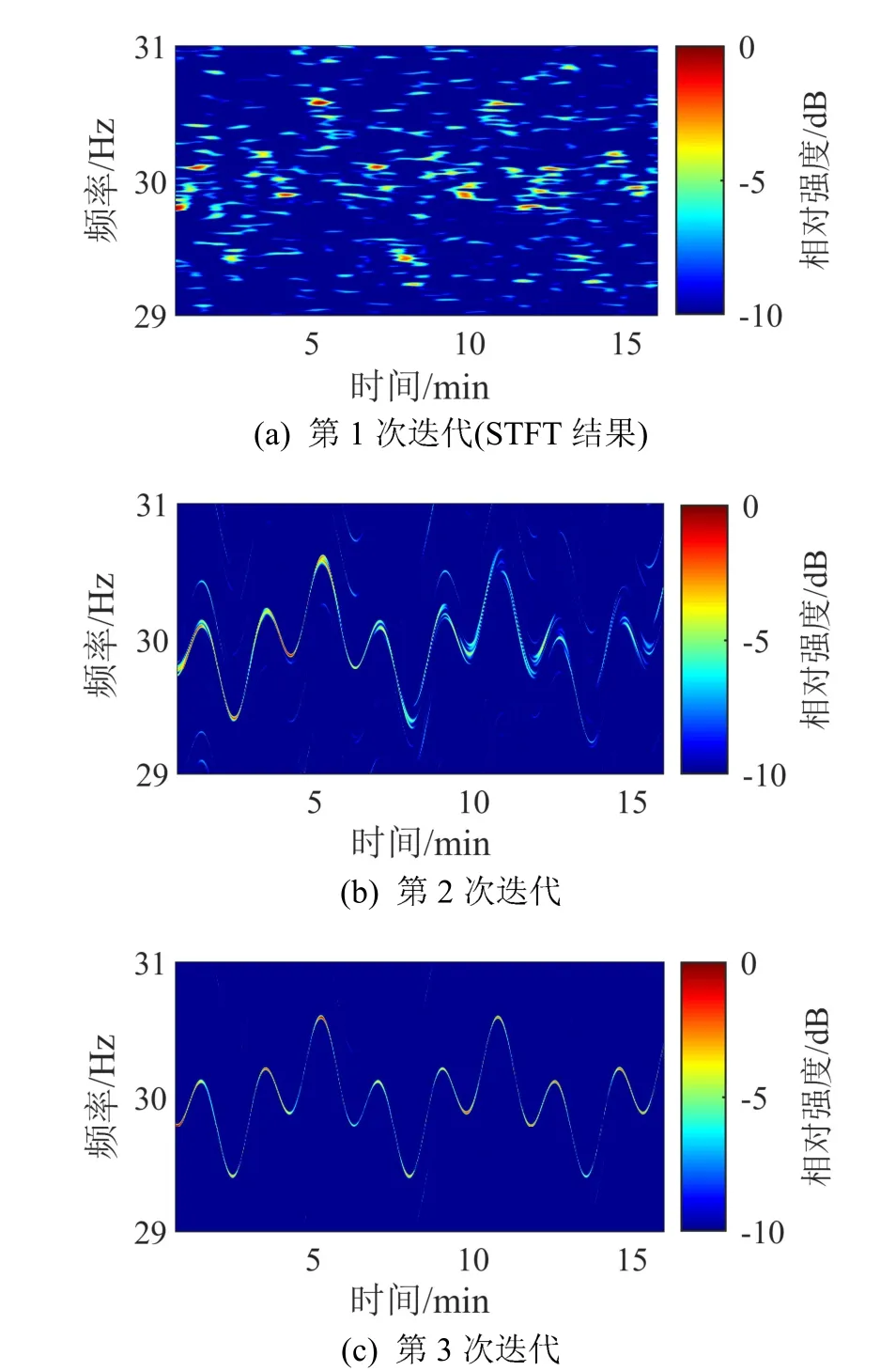
图3 仿真FMIPC-GWT 各次迭代输出结果 Fig.3 The simulation results for each interation of the FMIPC-GWT method

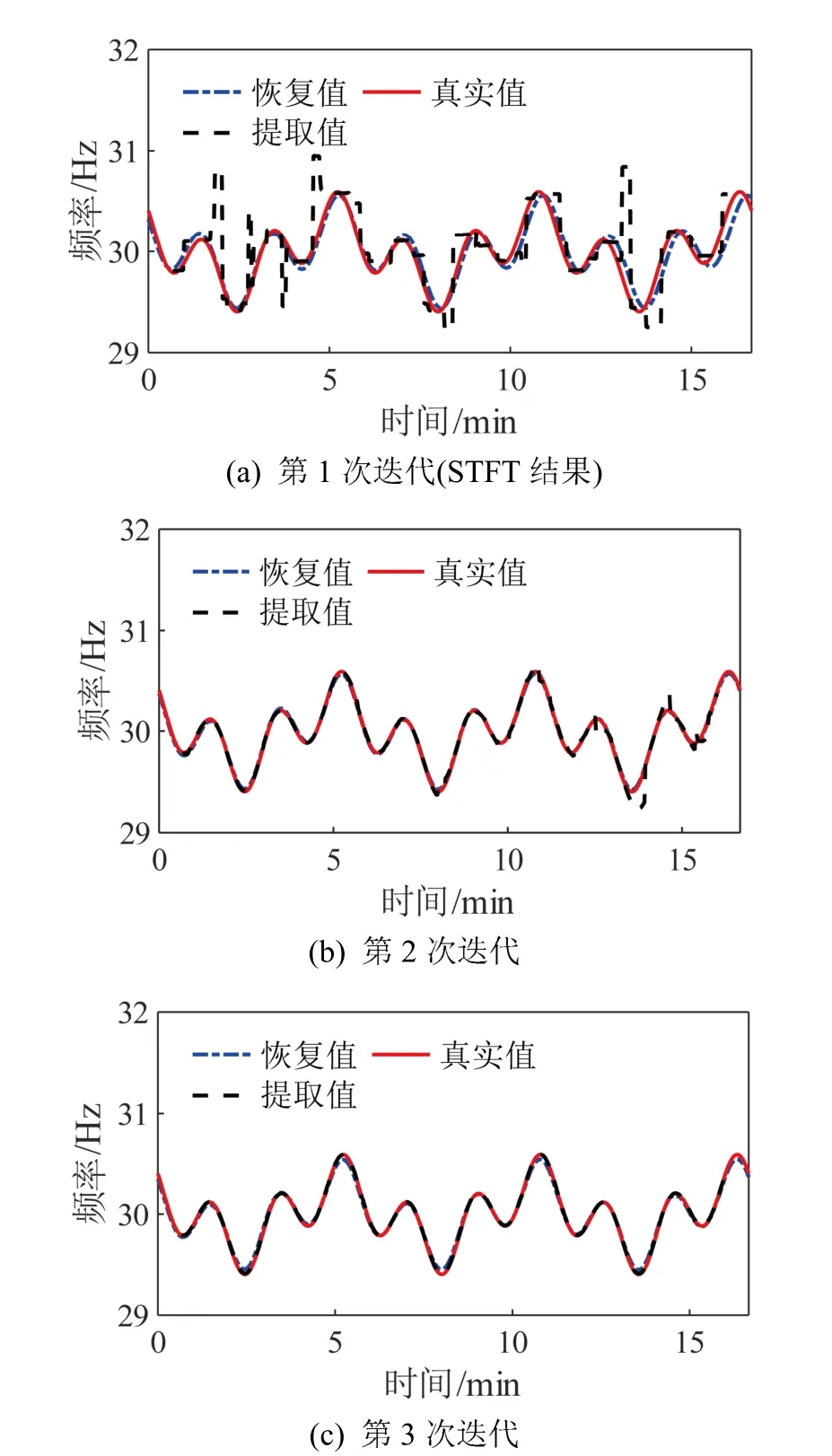
图4 FMIPC-GWT 各次迭代瞬时频率恢复值、真实值及 提取值对比 Fig.4 Comparison of the recovery,real and extracted values of the instantaneous frequency for each iteration of the FMIPC-GWT method

3.2 不同信噪比下算法性能分析

保持信号参数不变，通过调整噪声强度考察FMIPC-GWT 方法性能。利用蒙特卡洛（Monte Carlo）方法研究FMIPC-GWT 方法在不同信噪比条件下瞬时频率提取性能，谱级信噪比为−10～5 dB，按照1 dB 间隔分别进行100 次试验，Monte Carlo试验结果如图5 所示。图5 中，纵坐标表示可以准确提取瞬时频率的试验次数占比。由图5 可知，当谱级信噪比为−3 dB 时，FMIPC-GWT 方法仍有71%的可能正确输出，表明算法在较低信噪比下仍有较好性能。

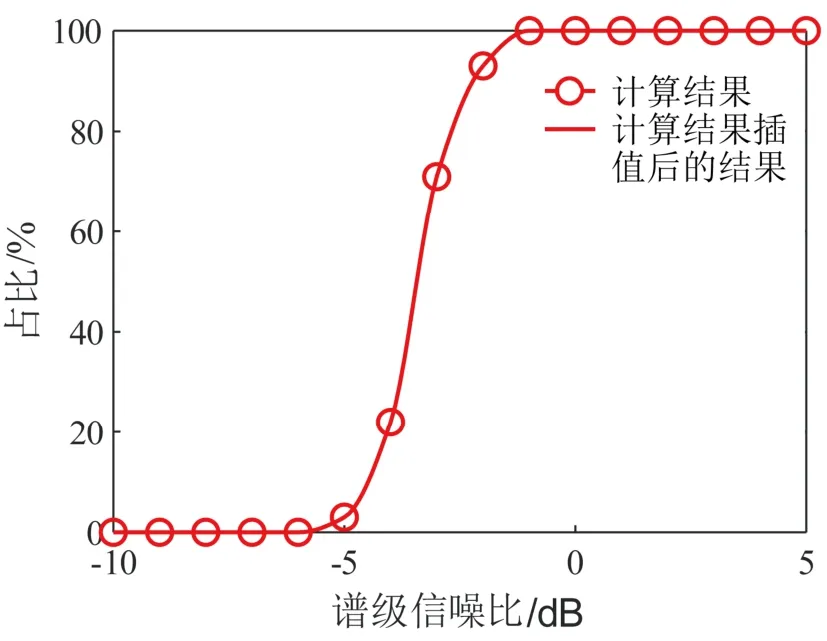
图5 不同信噪比下FMIPC-GWT 算法准确提取瞬时频率的占比 Fig.5 The proportion of accurately extracting instantaneous frequency by FMIPC-GWT method under different signal to noise ratios

4 实验数据处理

2018 年夏季，我们在某海域开展了一次水声实验观测过往船只辐射噪声，某时段接收噪声信号线谱具有瞬时频率时变特征。高斯时间窗长为16 000个数据点，每次向前滑动320 个数据点，时频分析算法共输出476 个时间采样点。利用式（5）在STFT结果中提取瞬时频率，对瞬时频率减去均值后做频谱分析如图6 所示，由高到低依次选取7 个峰值点所在频率作为调制频率。

图6 STFT 提取瞬时频率的频谱 Fig.6 The frequency spectrum of the instantaneous frequency extracted by STFT method

如不补偿调频初相位，直接对信号使用GWT算法即在调频参数估计时利用式（8）～（9）求调频幅度和调频初相位，迭代终止门限δ设为0.1%，最大迭代次数设为5，算法经过2 次迭代终止，分析结果如图7（a）～7（b）所示。图7（a）为STFT 结果，由于海洋环境噪声及信号瞬时频率随时间变化使线谱时频能量聚集度下降等因素，STFT 结果中线谱存在许多不连续的地方。由于未对1/2 个时间窗长引起的相位差进行补偿，使得调频参数估计结果与信号真实调频参数存在较大误差，旋转算子和平移算子与信号失配，GWT 法后续迭代结果并未改善STFT 的输出效果，甚至加剧了线谱的不连续性和时频能量分散程度。GWT 第2 次迭代的结果如图7（b）所示。对信号做相同时间窗长、相同滑动时间长度的FMIPC-GWT 处理即在调频参数估计时利用式（8）、（10）求调频幅度和调频初相位，迭代终止门限δ设为0.1%，最大迭代次数设为5，算法经2次迭代后终止，结果如图7（c）所示。相比STFT 和GWT 结果，FMIPC-GWT 结果线谱连续性更好，强度更高，FMIPC-GWT 算法可有效提高瞬时频率变化线谱时频能量聚集度，有利于提高时变线谱时间分辨率和频率分辨率。

图7 实验数据GWT/FMIPC-GWT 时频分析结果 Fig.7 Time-frequency analysis results of the experimental data obtained by GWT/FMIPC-GWT method

5 结论

本文针对GWT 算法在长时间窗处理时算法失效问题，提出一种调频初相位补偿的广义Warblet变换时频分析方法。通过在调频参数估计时将调频成分在1/2 时间窗长内经过的相位补偿到调频初相位估计值中，提高调频参数估计的准确性，避免因长时间窗处理导致旋转算子和平移算子与信号失配问题的出现，提高了瞬时频率时变信号线谱时频能量聚集度和频率分辨率。仿真和海上实验数据处理结果表明，FMIPC-GWT 方法能够避免GWT 方法在长时间窗分析时出现参数失配问题，在瞬时频率变化信号线谱检测中具有比STFT 和GWT 方法更优的性能。

FMIPC-GWT 方法需要的调频成分个数需要根据其瞬时频率轨迹的傅里叶变换结果给出。若选取的调制成分个数较少，则不足以描述瞬时频率的变化，算法输出信噪比下降。而如果选取的调制成分个数较多，则可能出现过拟合，降低瞬时频率估计的准确性。此外，当分析频带内存在较强的干扰线谱时，调频参数估计将出现错误导致算法失效，提高算法抗干扰能力将是未来的研究方向。

致谢感谢2018年夏季参加海上实验的全体同志，他们的辛勤工作为本文提供了宝贵的实验数据。