拉盖尔-高斯光束在高速运动分层介质中的传输特性

王明军，王婉柔 ，张 颖，柯熙政

(西安理工大学 自动化与信息工程学院，陕西 西安 710048)

随着电磁波技术的不断发展，电磁波在介质中的传输特性得到了人们的广泛关注.近些年来，一种特殊的光场走进了我们的视线，它的波面与我们常见的平面波和球面波不同，是螺旋结构的，也就是我们所说的涡旋光束.通过研究发现，它自身的螺旋形相位波前是由于其携带的轨道角动量(Orbital Angular Momentum，OAM)所导致的，这种独特的相位结构使其具有中心相位奇点，从而使它的光强呈现圆环型分布，使其在微粒操控、光通信、光子计算[1-3]、生物医学等众多领域中都发挥着重要作用.

关于涡旋光束在介质中的传输特性的研究，在2008年，Okuda等人[4]通过研究TM和TE 拉盖尔-高斯光束在接近临界入射的电介质界面处反射和透射，观察了反射光束和透射光束的强度分布情况.2011年，欧军等人[5]研究了在圆柱坐标系中傍轴线偏振LG光束在两种各向同性介质界面反射和折射后光强质心的偏移.2014年，张进等人[6]根据平面波角谱理论建立了涡旋光束在空气-玻璃界面反射时的傍轴传输模型.2017年，李海英、吴振森等人[7]基于角基于角谱扩展和4×4矩阵理论，研究了单轴各向异性多层介质中LG光束的反射和透射特性.2018年，刘佳伟、李海英、吴振森等人[8]研究了单轴各向异性介质层中矢量Bessel涡旋波束的传输特性.

随着对涡旋光束研究的愈发深入，可以看到其在介质中的传输取得了许多令人欣喜的成果.但这些研究大多都停留在静止介质以及单层介质中，并且大多都围绕其光强、幅度进行观察和讨论，很少对其相位的变化情况进行分析讨论.因此研究涡旋光束在分层介质以及高速运动分层介质中相位方面的传输特性是十分有必要的.

由于LG光束是目前应用范围最广且最为基础的涡旋光束，任意涡旋光束都可以分解为若干个LG光束，并且分解后的LG光束相互独立，互不干扰.而线偏振的LG光束产生简单，便于分析.因此本文将以线偏振的矢量LG光束为例，分别对LG光束在自由空间、静止分层介质以及高速运动介质上的传输特性进行研究，主要研究其相位特性，讨论其相位变化情况.

1 涡旋光束的传输特性

1.1 涡旋光束在自由空间中传播

已知LG光束沿z轴传播时，在柱坐标系中的电场表达式为

(1)

式中，n为径向模式分量；l为弧向模式分量也称为拓扑荷数；p0为激光器的功率；θ为LG光束的方位角；w(z)为在z处的束腰半径.

假设光束沿z轴正向传播，从z=0处发射，根据式(1)，LG光束的电场表达式可以写为

(2)

由惠更斯-菲涅尔原理和ABCD传输矩阵可以得到z处涡旋光束的电场为

(3)

其中k为波数，ABCD为系统的传输矩阵.

将式(2)代入式(3)中，整理可得[9]

(4)

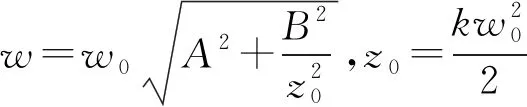
(5)

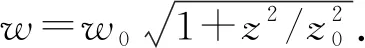
由式(5)可以看出，涡旋光束在自由空间中传播时，其相位因子exp(ilφ)依旧存在并未发生改变，故在自由空间中传播时，涡旋光束的相位依旧会随着方位角的变化而变化，呈现螺旋结构.

1.2 涡旋光束在静止分层介质上的传输特性

假设入射光束为沿z轴正向传播的线偏振矢量涡旋光束.首先我们对静止分层介质进行研究，由于任意方向入射的电磁波都可以分解成为电场与入射面平行的平行极化波和电场与入射面垂直的垂直极化波，以此为依据将入射LG光束进行分解.图1为垂直极化波入射至静止分层介质的模型[10].

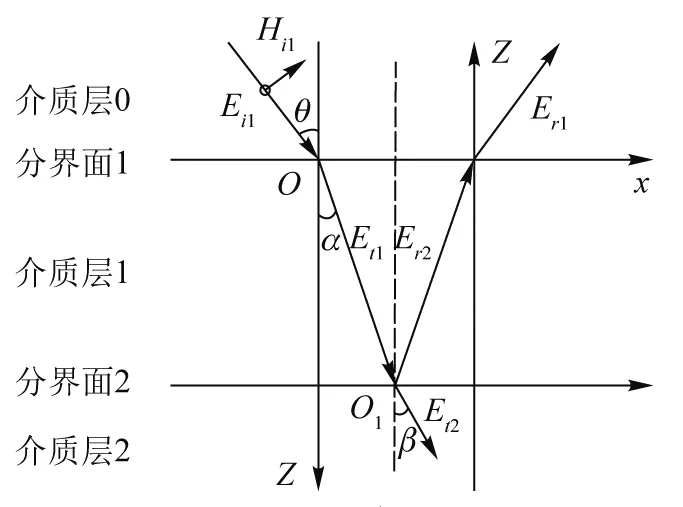
图1 LG光束入射至静止分层介质模型

将涡旋光束所携带的相位因子eilθ分解为每个平面波谱所携带的相位eilv，则可将其相位分布表示为[11]

φ(k)=eilv=eilarctan(ky/kx)

(6)

式中arctan(ky/kx)∈(-180°,180°).

对于入射波，其波矢量ki可以分解为

(7)

其中θ为入射角，v为涡旋光束的方位角.

由式(6)可得其相位分布为

φi(ki)=eilv=eilarctan(kiy/kix)

(8)

令：

则由式(1)和式(8)可得，入射垂直极化波电场表达式为

Ei1⊥=(axcosθ-azsinθ)Elgφi(ki)e-i(xkix+zkiz)=

(axcosθ-azsinθ)Elgeilarctan(kiy/kix)e-i(xkix+zkiz)

(9)

入射平行极化波电场表达式为：

Ei1‖=ayElgφi(ki)e-i(xkix+zkiz)=

ayElgeilarctan(kiy/kix)e-i(xkix+zkiz)

(10)

对于反射波，根据坐标变换，可得到入射波矢量与反射波矢量的坐标变换关系为：

(11)

由式(6)可得其相位分布为：

φr(kr)=eilv=e-ilarctan(kry/krx)

(12)

由Erm⊥=R⊥×Ei1⊥可得，反射垂直极化波电场表达式为：

Erm⊥=R⊥(axcosθ-azsinθ)Elgφr(kr)e-i(xkrx+zkrz)=

R⊥(axcosθ-azsinθ)Elge-ilarctan(kry/krx)e-i(xkrx+zkrz)

(13)

由Erm∥=R∥×Ei1∥，可得反射平行极化波电场表达式为

Erm∥=R∥ayElgφr(kr)e-i(xkrx+zkrz)=

R∥ayElge-ilarctan(kry/krx)e-i(xkrx+zkrz)

(14)

对于透射波，同理可得其透射波矢量与入射波矢量的坐标变换关系为：

(15)

式中τ为透射角，θ为入射角，其关系为：sinθ=nsinτ.

特别地，当θ=0时，可将式(15)写为：

(16)

由式(6)可得其相位分布为

φt(kt)=eilv=eilarctan(kty/ktx)

(17)

由Etm⊥=T⊥×Ei1⊥可得，透射垂直极化波电场表达式为

(18)

由Etm∥=T∥×Ei1∥可得，透射平行极化波电场表达式为：

Etm∥=T∥ayElgφt(kt)e-i(xktx+zktz)=

T∥ayElgeilarctan(kty/ktx)e-i(xktx+zktz)

(19)

由式(8)和式(12)可以看出，入射涡旋波和反射涡旋波的拓扑荷数相反，因此入射涡旋波和反射涡旋波的相位旋转方向应该相反.由式(8)和式(16)可以看出，入射涡旋波和透射涡旋波具有相同的拓扑荷数，因此其相位旋转方向应该相同.但由于波矢量不再具有线性关系，因此方位角将不再线性变化.

1.3 涡旋光束在高速运动分层介质中的传输特性

假设S系为参考坐标，在S′系中的各向同性介质以v的速度向x轴正向运动，建立如图2所示坐标系.入射LG光束以θ为入射角x′O′z′平面为入射面，由介质0进入介质1中.其中k为波矢量，θ、α分别为入射角和透射角.

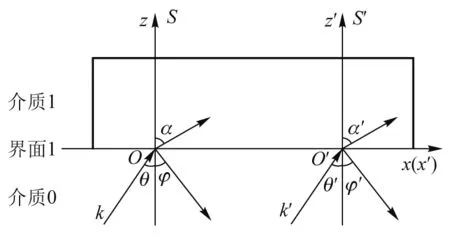
图2 运动分层界面模型

由于在高速运动过程中，电磁场量会发生变化，故根据洛伦兹逆变换可得：

(20)

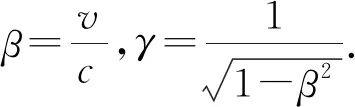
由式(20)可得，电场强度满足：

E=γ(1+βcosθ′)E′

(21)

波矢量k满足：

ω=γ(ω′+vk′x)

(22)

当入射波是垂直极化波时，在S′系中有E′i=E′ixax+E′izaz，将其变换到S系中，可得[12]：

Ei⊥=γ(1+βcosθ′)E′i⊥=

γ(1+βcosθ′)(E′ixax+E′izaz)=

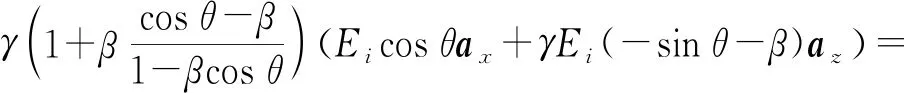
(23)

(24)

(25)

当入射波为平行极化波时，在S′系有E′i=E′iyay，由洛伦兹变换将其变换到S系中，可得：

(26)

(27)

(28)

式中R⊥v、T⊥v、R∥v、T∥v分别为垂直极化波和平行极化波在运动分层介质中的反射系数和透射系数.

为保证推导的正确性，将高速运动分层介质中所推导的反射和透射波表达式进行退化.由式(20)可知，当v=0时，β=0，γ=1，则对于垂直极化波，式(23)、式(24)和式(25)可以分别退化为1.2节中的式(9)、式(13)和式(18)静止分层介质中入射、反射和透射垂直极化波表达式. 同理对于平行极化波，当v=0时，式(26)、式(27)和式(28)也可以分别退化为式(10)、式(14)和式(19). 即就是当介质运动速度为0时，高速运动分层介质中所推导表达式都可以退化为静止时的表达式，即可验证推导的正确性.

2 数值模拟

取LG光束的径向分量n=0，拓扑荷数l=2，束腰半径ω0=0.5mm，以式(13)、(18)为研究基础，用matlab进行数值模拟.图3-图6为LG光束入射至静止各向同性分层介质时，改变其入射角对反射光束和透射光束的相位影响情况. 此处只给出垂直极化波的数值模拟结果，水平极化波变化规律与垂直极化波相同.

图3可以看出，当入射角为0°时，反射涡旋光束的相位旋转方向和入射光束的相位旋转方向相反，与之前得到的结论相符，由此时没有透射涡旋光束. 由图3-图6可以看出，通过增大入射角，反射涡旋光束的相位除了旋转方向与入射涡旋光束相反之外，一直维持涡旋光束的相位结构；而透射涡旋光束的相位会随着入射角的增大，相位结构逐渐模糊，逐渐失去涡旋光束所具有的相位特点，当入射角大于等于45°时彻底丢失其相位结构.

图3 入射角为0°时相位图

图4 入射角为30°(π/6)时相位图

图5 入射角为36°(π/5)时相位图

图6 入射角为45°(π/4)时相位图

以式(24)和式(25)为研究基础，对LG光束入射至高速运动分层界面的情况进行数值模拟，图7-图10为当θ=0，介质运动速度改变时LG光束的相位变化情况.

由图7-图10可以看出，无论介质静止还是运动，反射涡旋光束的相位旋转方向都和入射光束相反；透射光束的相位旋转方向和入射光束相位旋转方向相同. 当介质静止，入射角为0时，没有透射涡旋光束；当介质开始高速运动，此时入射和反射涡旋光束的旋转方向与静止时恰好相反，并且出现透射涡旋光束，这是由于介质的运动速度对涡旋光束的波矢产生了影响，改变了涡旋光束的传播方向,从而使其出现透射光束.当介质速度逐渐增大，入射涡旋光束和反射涡旋光束的相位改变逐渐减小，与我们的公式推导结果相符.

图7 介质运动速度v=0 m/s

图8 介质运动速度v=0.5×106 m/s

图9 介质运动速度v=0.5×107 m/s

图10 介质运动速度v=0.5×108 m/s

3 结论

本文主要对线偏振的LG光束在介质中相位的传输特性进行分析推导.首先讨论了自由空间中涡旋光束的相位变化情况.随后对其在静止分层界面以及高速运动界面上的反射涡旋光束和透射涡旋光束的相位变化情况进行了推导，发现反射光束的拓扑荷数与入射光束的拓扑荷数相反，故其相位旋转方向与入射光束相反；透射光束的拓扑荷数与入射光束的拓扑荷数相同，但波矢量呈非线性关系，透射光束将不在具备入射光束的圆形轴对称分布特点.并且当介质运动速度为0时，高速运动分层介质中所推导表达式都可以退化为静止时的表达式. 最后通过数值模拟，验证了静止分层界面以及高速运动界面情况结论的正确性，并模拟当入射角增大时，反射涡旋光束和透射涡旋光束在静止分层界面的相位变化情况，发现当入射角逐渐增大，反射涡旋光束的相位除了旋转方向与入射涡旋光束相反之外，将一直维持涡旋光束的相位结构；而透射涡旋光束的相位会随着入射角的增大，相位结构逐渐模糊，逐渐失去涡旋光束所具有的相位特点，当入射角大于45°时彻底丢失其相位结构. 当介质静止，入射角为0时，此时没有透射涡旋光束；当介质开始高速运动，此时入射和反射涡旋光束的旋转方向与静止时恰好相反，并且由于介质的运动速度对涡旋光束的波矢产生了影响，出现了透射涡旋光束. 当介质速度逐渐增大，入射涡旋光束和反射涡旋光束的相位改变逐渐减小.本文的研究结果详细的给出了线偏振的LG光束在自由空间、单层介质、高速运动介质以及多层介质上传输时的相位变化情况，进一步完善了涡旋光束的相位在介质中的传输特性，对后续研究十分有意义.另外，若后续需对其他偏振状态进行研究，比如圆偏振状态，可以参考本文对线偏振涡旋光束的研究，将其分解为两个振动方向互相垂直的线偏振光进行分析.