水平旋转弹簧的临界角速度
2022-07-26赵冬秋贾拴稳秦绪明
赵冬秋,贾拴稳,秦绪明,袁 地,董 浩
(安阳师范学院 物理与电气工程学院,河南 安阳 455000)
弹簧振子是一种常用的物理模型,其中的弹簧通常被默认为轻质弹簧.但严格来讲,弹簧的质量不可被忽略,否则会对力场中弹簧系统产生影响.近来,弹簧质量对弹簧系统影响的研究引起了人们的关注.于凤军教授应用最小势能原理研究了重力场中有重弹簧静止时的质量分布和质心位置问题[1].罗兴垅等则从力的平衡条件出发对该问题进行了探讨,得到了一致的结论[2].这些方法为力场中弹簧运动的研究提供了思路和参考.最近,呼格吉乐等根据力的平衡条件对绕固定端旋转的有重弹簧进行探究,给出了旋转弹簧长度与角速度的关系式[3][见文献[3]式(10)].
然而目前的研究也存在某些问题,文献[3]把临界角速度定义为弹簧长度趋向无穷时所对应的角速度,是不恰当的,也不符合实际物理情况.这是因为,弹簧在其弹性限度内弹力和形变量服从胡克定律,超过弹性限度,不但胡克定律以及由其导出的公式不成立,甚至可能会被损坏.如何定义符合实际的临界角速度,并导出其表达式,如何判断弹簧是在安全范围内使用,将是本文研究的问题.
1 旋转弹簧的长度和临界角速度定义
设一匀质圆柱形弹簧,质量为m,劲度系数为k,原长为l0,当它静止于水平面上时在弹性限度内的极限长度是lc.将弹簧一端固定于原点O,另一端是自由端,在弹簧上沿其轴线建立Ox坐标轴,如图1所示.让弹簧在水平面内绕O点以角速度ω稳定旋转.假定:当ω=0时,弹簧上各点位置用x表示(0≤x≤l0);当ω≠0时弹簧上位置为x的点A沿轴向位移为u(x).则A点到O点的距离y为

图1 弹簧示意图
y=x+u(x)
(1)
在点A附近取长为dx的一段线元,其质量是dm=λdx,其中λ=m/l0.在与弹簧一起匀速旋转的参考系中,线元受惯性离心力和弹性力作用,惯性离心力的大小为ω2ydm,其相关的势能(取O为势能零点)是(-1/2)ω2y2dm=(-1/2)λω2(x+u)2dx.线元伸长量为du=u(x+dx)-u(x),该线元的劲度系数[1]表示为kl0/dx,则弹性势能是(1/2)(kl0/dx)(du)2=(1/2)kl0(u′)2dx,故体系总能量V为
(2)
点x处弹力为
F(x)=kl0u′(x)
(3)

kl0u″+λω2(x+u)=0
(4)
(5)
弹簧形变满足的第一个边界条件是原点固定,弹簧的形变量为零:u(0)=0.第二个边界条件是弹簧末端的弹性力F(l0)为零,这是由于弹簧末端为不受约束的自由端.由此及式(3)可得弹簧系统满足的边界条件是
(6)
把式(5)代入式(6)可解出C1、C2,再将C1、C2的解代入式(5)得
(7)
结合式(7)和式(1)得到弹簧的长度分布为
(8)
所以弹簧总长度是
(9)
图2表示根据式(9)画出的弹簧长度与角速度的函数关系曲线.由图2可知,当ω=0时,弹簧长度等于原长.随着ω的增加,其长度单调增加.当ω/ω0→π/2时,弹簧长度趋于无限长.显然从物理上讲这是不可能的,因为弹簧早已超过其弹性限度,随着ω的逐渐增加,上边的讨论和导出的公式已经不能成立.因此存在某一角速度ωc,当ω<ωc时,胡克定律成立;当ω>ωc时,胡克定律不成立.我们把ωc叫做旋转弹簧的临界角速度,此时对应的弹簧长度Lc叫旋转弹簧的临界长度.下面将导出ωc和Lc的表达式.

图2 水平旋转弹簧长度与角速度的曲线图
2 旋转弹簧的弹力分布和临界参数的确定
(10)
图3表示根据式(10)画出的当ω/ω0=π/3时弹簧上弹力随x的变化曲线.由图3可知弹簧末端的弹力为零,这是因为弹簧末端为自由端.其余位置的弹力随x的增加而减小.弹簧上最大弹力位置在原点(见图3),对应的弹力为

图3 当ω/ω0=π/3时,弹簧上弹力F(x)随x的变化曲线
(11)
前面已经假定水平静止弹簧在弹性限度内的极限长度即能使胡克定律成立的极限长度为lc.根据胡克定律,可推知该弹簧任意位置所能承受的极限弹力是
Fc=k(lc-l0)
(12)
当有重弹簧于水平面内旋转时,由于惯性离心力的作用,弹簧上弹力分布不均匀.显而易见,旋转弹簧上任一点的弹力不能超过Fc,否则它将不满足胡克定律,并且有可能被损坏.由于弹簧最大弹力位置在原点(见图3),故为了使胡克定律在旋转弹簧中的所有点成立,要求
Fmax=F(0) (13) ωc=ω0arccos(l0/lc) (14) 用式(14)中ωc取代式(9)中ω就得到旋转弹簧的临界长度,即 (15) 2) 式(14)表明ωc∝ω0,即在l0/lc相同情况下,弹簧的劲度系数越大(俗话说弹簧越硬),角速度的临界值越大,弹簧不容易被损坏,这符合人们的生活经验. 小结:以上指出了目前文献在研究旋转弹簧临界角速度问题上的不妥之处.根据胡克定律成立的条件给出了旋转弹簧的临界角速度的定义.由最小势能原理导出旋转弹簧上各点的位移分布,并由该位移分布导出弹簧上各点的弹力分布.最后根据弹力分布和临界参数的定义得到旋转弹簧的临界角速度表达式(14)和临界长度表达式(15),并进行相关问题的讨论,得出结论:对于质量不能忽略的弹簧,无论是旋转状态还是悬挂状态,其临界长度均小于它处于水平静止状态下在弹性限度内的极限长度. 致谢: 感谢于凤军教授耐心细致的指导.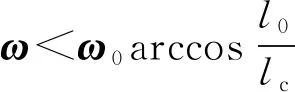
3 讨论


