有伴电源Y-△联结等效变换研究
2022-07-26沈一骑
万 凯,沈一骑
(1. 南京大学 商学院,江苏 南京 210093;2. 南京大学 电子科学与工程学院,江苏 南京 210023;3. 南京大学 金陵学院,江苏 南京 210089 )
电源等效变换分析法是电路分析的重要方法之一,也是电路分析基础教学的一个重要环节. 电源等效变换分析法特别适用于多电源的串并联电阻电路,可以通过电源变换使电源满足合并要求,从而将多电源电路简化为单电源电路以便于分析. 但对多电源的Y-△联结电阻电路就难以处理了,而且众多理论教材[1,2]均不涉及这一问题,这就造成了电源等效变换分析法应用的局限性,也给学生学习带来了困惑. 对此,我们在多年电路教学和研究[3],[4]的基础上,提出了有伴电源Y-△联结电路等效变换理论推导,以供参考和指正.
1 有伴电压源Y-△联结等效变换理论推导
1.1 有伴电压源△形电路等效变换
有伴电压源△形电路如图1(a)所示. 等效变换是对外等效,如果对节点1、2、3内的电路进行等效变换,就可保持节点外电路的状态不变. 由于各支路为有伴电压源,各电阻并不构成△形联结,可将各支路等效为有伴电流源(图1(b)),其中IS12=US12/R12、IS23=US23/R23、IS31=US31/R31. 为满足Y-△形电阻等效变换的要求,已将节点拆分为2个相连的节点,节点1′、2′、3′构成的△形电路,可参照教材的变换公式[1]对外等效为Y形电路(图1(c)). 合并拆分的节点并采用电源转移方法[2],将图1(c)中的电流源转移至相邻支路(图1(d)),再合并电流源(图1(e)),其中IS1=IS12-IS31、IS2=IS23-IS12、IS3=IS31-IS23,最后等效为有伴电压源的Y形电路,如图1(f)所示.
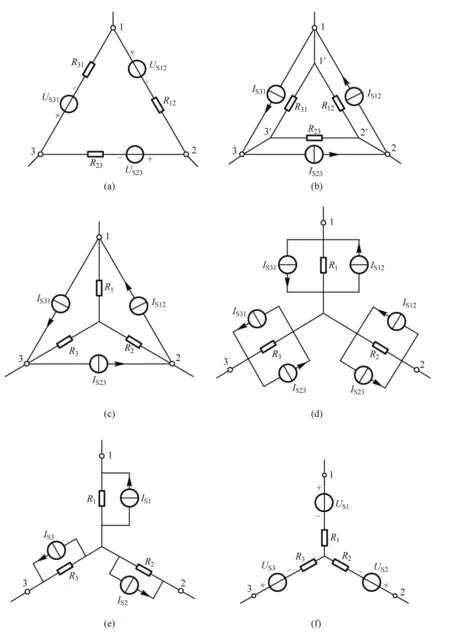
图1 有伴电压源△形电路等效变换
其中
(1)
(2)
1.2 有伴电压源Y形电路等效变换
对于图1(f)所示的有伴电压源Y形电路,可先将其内部Y形电阻电路等效为△形电路(图2(a)),再利用电源转移法[2],将图2(a)中各电压源转移到相邻支路中去,即图2(b),最后合并各支路的电压源,得到图1(a)所示的有伴电压源△形电路.

图2 有伴电压源Y形电路等效变换
其中
(3)
(4)
2 无伴电源Y-△联结等效变换理论推导
由于有伴电流源可等效为有伴电压源,电流源串联电阻对外等效可舍去其串联电阻,Y-△联结电路的含源支路除了有伴电压源外,还有无伴电压源和无伴电流源两种形式. 采用适当方法可从有伴电压源Y-△等效变换公式直接推出各种情况的变换算式. 因为无伴电压源的串联电阻为0、无伴电流源的并联电阻为∞,在计算中可将0值电阻设为极小电阻R0、∞值电阻设为极大电阻R∞,计算后再令R0=0和R∞=∞. 此外,若电压源US=0,则电压源为短路;电流源IS=0,则电流源为开路. 以含无伴电压源和无伴电流源的Y形电路为例,如图3(a)所示:设R1=R1∞=∞、R2=R20=0,则由式(3)可得R12=R1∞(1+R20/R3)=R1∞、R23=R3(1+R20/R1∞)=R3、R31=R1∞(1+R3/R20)=R1∞R3/R20;由式(4)可得:US12=R1∞IS1、US23=US2-US3、US31= -R1∞IS1. 由于变换所得为有伴电压源△形电路,故须对变换后有阻值为∞的支路再变换为有伴电流源,故IS12=US12/R12=R1∞IS1/R1∞=IS1,并联电阻为R12=∞;IS31=US31/R31=-R1∞R20IS1/R1∞R3=-R20IS1/R3=0,并联电阻为R31=∞,显然支路31为开路. 最后所得的△形等效电路如图3(b)所示.

图3 含无伴电源Y形电路等效变换
3 有伴电源Y-△联结等效变换一览表
为方便应用,表1给出了常见有伴电源Y-△联结的等效变换,从中也可以推出含无伴电压源的变换电路和算式. 需要说明的是,表1“有伴电压源的Y形和△形电路”由Y→△(或△→Y)的变换是单向的,即先作Y→△,再由△→Y变换到Y(记为Y′),Y和Y′形电路中的电源参数是不同的,这是因为Y→△变换中用到了无伴电压源转移变换,△→Y变换中用到无伴电流源转移变换,而这两种电源转移变换之间并不是等效变换. 但Y→△和△→Y都是对外等效的,若将Y、△和Y′接入相同的外电路,外电路的响应将保持不变. 此外,Y和Y′形电路中的电阻参数保持不变,是因为在变换中电阻本身只作了运算,没有变换. 同理,表1中的其他变换亦是单向的, 示例如图4所示.
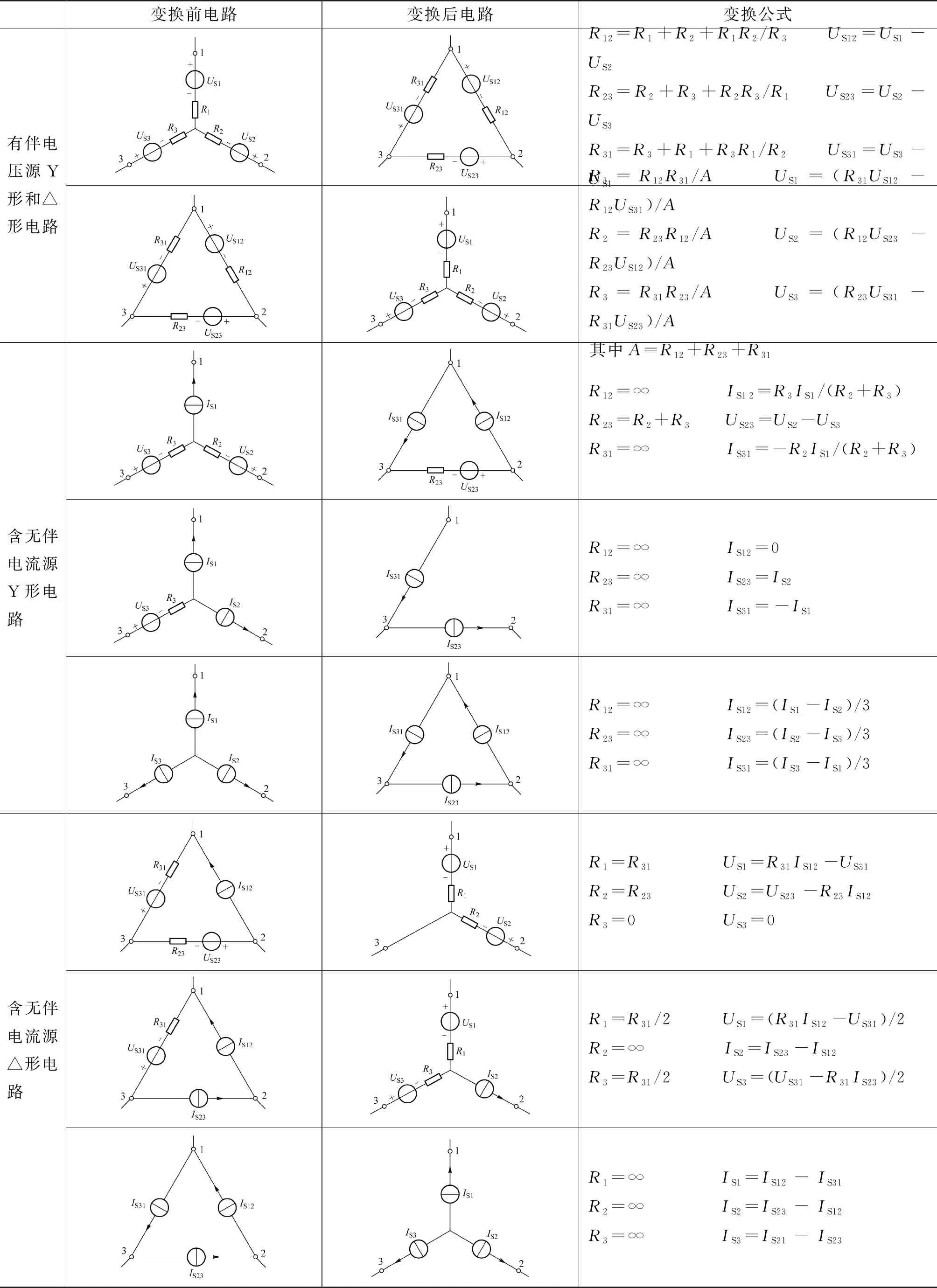
表1 有伴电源Y-△联结等效变换
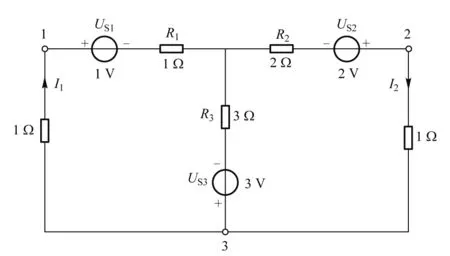
Y形
计算表明图4中各电路均有
4 结束语
为将电源等效变换分析法的应用从含源串并联电阻电路拓展为含源Y-△联结电路,以便于学生学习和分析电路,我们研究了有伴电源Y-△联结的等效变换,包括有伴电压源Y-△联结等效变换和各支路含无伴电压源和无伴电流源的等效变换. 这一变换还可用于含内阻三相电源的等效和含源二端口网络的分析.
