借数学建模之风 提升核心素养

◎吴龙泽

(华南师范大学数学科学学院,广东 广州 510631)

一、问题的提出

“数学建模”虽是老话重提，但是在新课标中的地位越发显著.它是数学学科核心素养之一，是应用数学知识解决实际问题的基本手段，是推动数学发展的外部驱动力.从现实性来看，华罗庚先生在《大哉，数学之为用》一文中说：“宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，生物之谜，日用之繁，无处不用数学.”数学来源于生活，又服务于生活.从文化性来看，南开大学顾沛教授曾指出数学不仅包含数学思想、方法等，还包含数学史，数学与社会、各种文化等的联系.从选拔性考试来看，近几年高考数学建模试题比重增大，难度增加，综合性增强，能力要求更高，突出实际应用，在高考中举足轻重.

基于较长时间的个人观察和感悟，通过与一线教师、教研员的交流，笔者发现学生在数学建模这一模块的学习效果与教师的期望值有着一定的偏差，所以笔者以此为出发点，致力于研究学生在数学建模方面所表现出的特点和不足.

二、数据收集

选取2019年人教A版高中数学必修第一册第4章的数学建模——建立函数模型解决实际问题这节课，研究内容是建立高一学生身高与体重的函数模型.在高一10个班级里随机抽取3个班，以不记名的方式记录每位学生的性别、身高和体重，身高单位是cm，体重单位是kg，研究对象有131人.

三、结果与分析

在分析过程中，只考虑体重与身高的关系，忽略地域、年龄等其他因素的影响.运用MATLAB数学软件对数据进行分析.其结果如下：全部研究对象的身高(cm)和体重(kg)的最大值分别是184和86，最小值分别是148和36，算术平均值分别是165.2748和56.6870，几何平均值分别是165.0828和55.8430，和谐平均值分别是164.8920和55.0474，调整平均值分别是165.2636和56.6202，回归系数的最小二乘估计是0.3440，其95%置信度的置信区间是[0.3350，0.3531]，其散点图如图1所示.

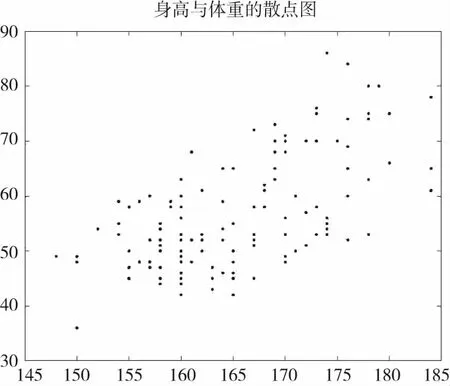
图1

根据高一学生所学函数和散点图特点对其函数模型进行拟合，拟合结果如下：

拟合结果相差不大，模型虽然不是很理想，但是相对而言，正弦型函数的拟合效果最好.

General model Fourier1:f(x)=a0+a1*cos(x*w)+b1*sin(x*w)

Coefficients(with 95% confidence bounds):

a0=60.57(55.05，66.09)

a1=8.642(-53.08，70.36)

b1=-6.715(-93.84，80.41)

w=0.09762(0.03779，0.1574)

其拟合后的图像如图2所示.

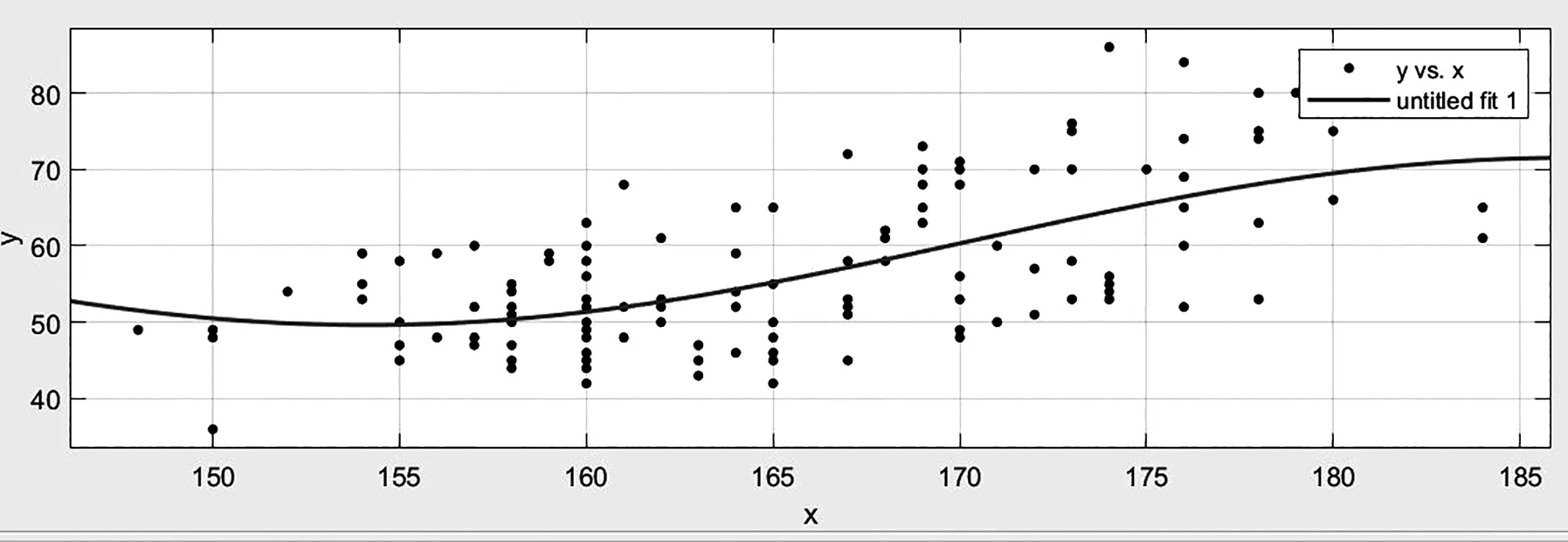
图2

因为男生和女生的生长速度和机能有所不同，所以把研究对象131名学生按性别区分，其中男学生66名，女同学65人.分析结果如下：男同学的身高(cm)和体重(kg)的最大值分别是184和86，最小值分别是158和45，算术平均值分别是171.5303和62.7121，几何平均值分别是171.4378和61.9145，和谐平均值分别是171.3451和61.1229，调整平均值分别是171.5469和62.6250，回归系数的最小二乘估计是0.3660，其95%置信度的置信区间是[0.3524，0.3795]，其散点图如图3所示.

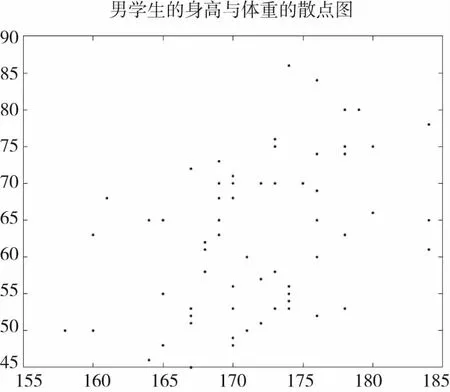
图3

对其函数模型进行拟合，拟合结果如下：

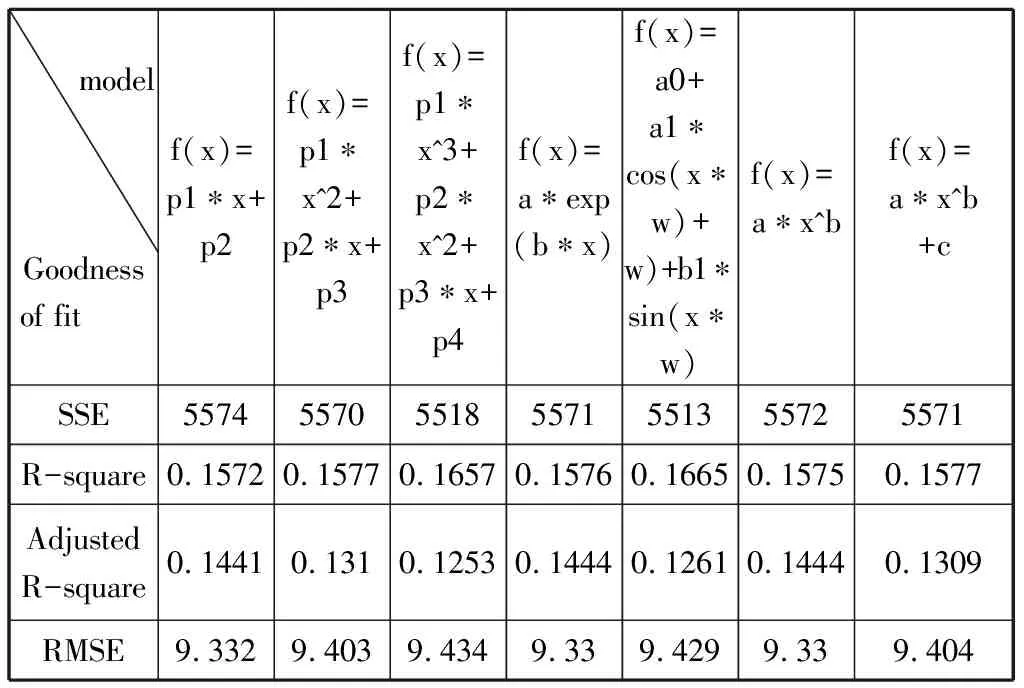
modelGoodnessof fit f(x)=p1∗x+p2f(x)=p1∗x^2+p2∗x+p3f(x)=p1∗x^3+p2∗x^2+p3∗x+p4f(x)=a∗exp(b∗x)f(x)=a0+ a1∗cos(x∗w)+w)+b1∗sin(x∗w)f(x)=a∗x^bf(x)= a∗x^b+cSSE5574557055185571551355725571R-square0.15720.15770.16570.15760.16650.15750.1577AdjustedR-square0.14410.1310.12530.14440.12610.14440.1309RMSE9.3329.4039.4349.339.4299.339.404

拟合结果相差不大，模型虽然不是很理想，但是相对而言，比上面全部同学的数学模型拟合效果更好，其中正弦型函数的拟合效果最好.

General model Fourier1:f(x)=a0+a1*cos(x*w)+ b1*sin(x*w)

Coefficients(with 95% confidence bounds):

a0=63.35(57.93，68.77)

a1=0.347(-186.5，187.2)

b1=6.82(-0.4588，14.1)

w=0.1455(-0.01495，0.3059)

其拟合后的图像如图4所示.

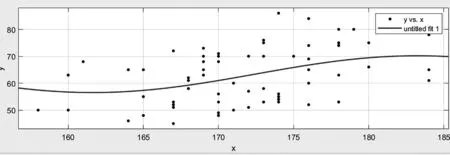
图4

女同学的身高(cm)和体重(kg)的最大值分别是167和61，最小值分别是148和36，算术平均值分别是158.9231和50.5692，几何平均值分别是158.8710和50.2869，和谐平均值分别是158.8186和50.0009，调整平均值分别是158.9683和50.6349，回归系数的最小二乘估计是0.3180，其95%置信度的置信区间是[0.3095，0.3265]，其散点图如图5所示.

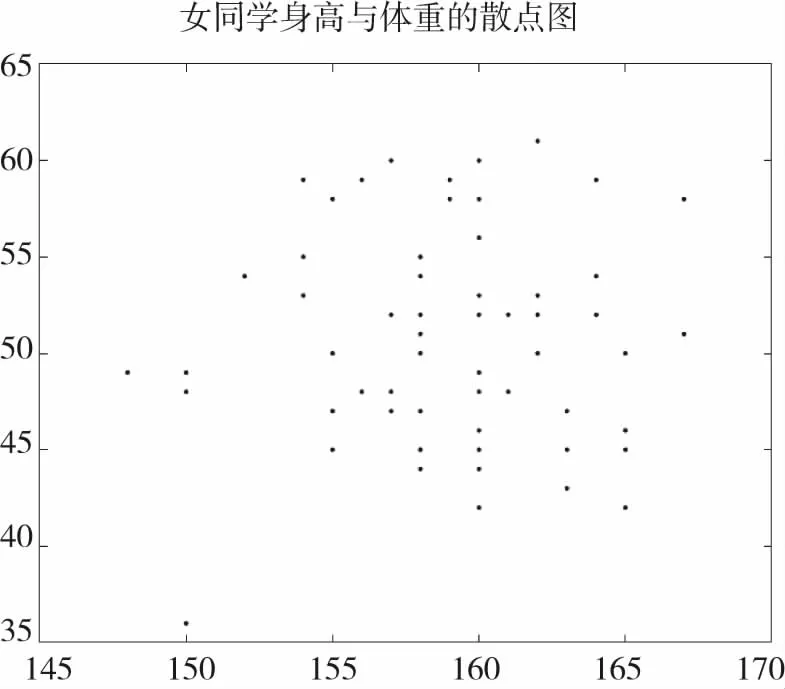
图5

对其函数模型进行拟合，拟合结果如下：

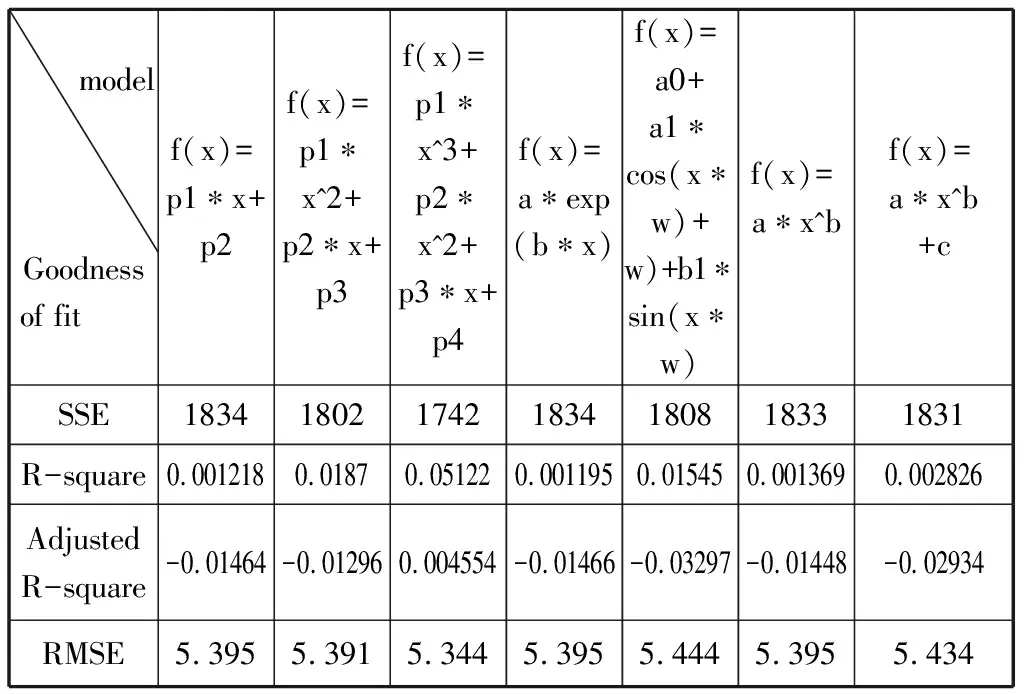
modelGoodnessof fit f(x)=p1∗x+p2f(x)=p1∗x^2+p2∗x+p3f(x)=p1∗x^3+p2∗x^2+p3∗x+p4f(x)=a∗exp(b∗x)f(x)=a0+ a1∗cos(x∗w)+w)+b1∗sin(x∗w)f(x)=a∗x^bf(x)=a∗x^b+cSSE1834180217421834180818331831R-square0.0012180.01870.051220.0011950.015450.0013690.002826AdjustedR-square-0.01464-0.012960.004554-0.01466-0.03297-0.01448-0.02934RMSE5.3955.3915.3445.3955.4445.3955.434

拟合结果相差不大，模型虽然不是很理想，但是相对而言，三次函数的拟合效果最好.

Linear model Poly3:f(x)= p1*x^3 + p2*x^2 + p3*x + p4

Coefficients(with 95% confidence bounds):

p1=0.008315(-0.003185，0.01982)

p2=-3.968(-9.414，1.478)

p3=630.7(-228.5，1490)

p4 = -3.335e+04(-7.851e+04，1.181e+04)

其拟合后的图像如图6所示.

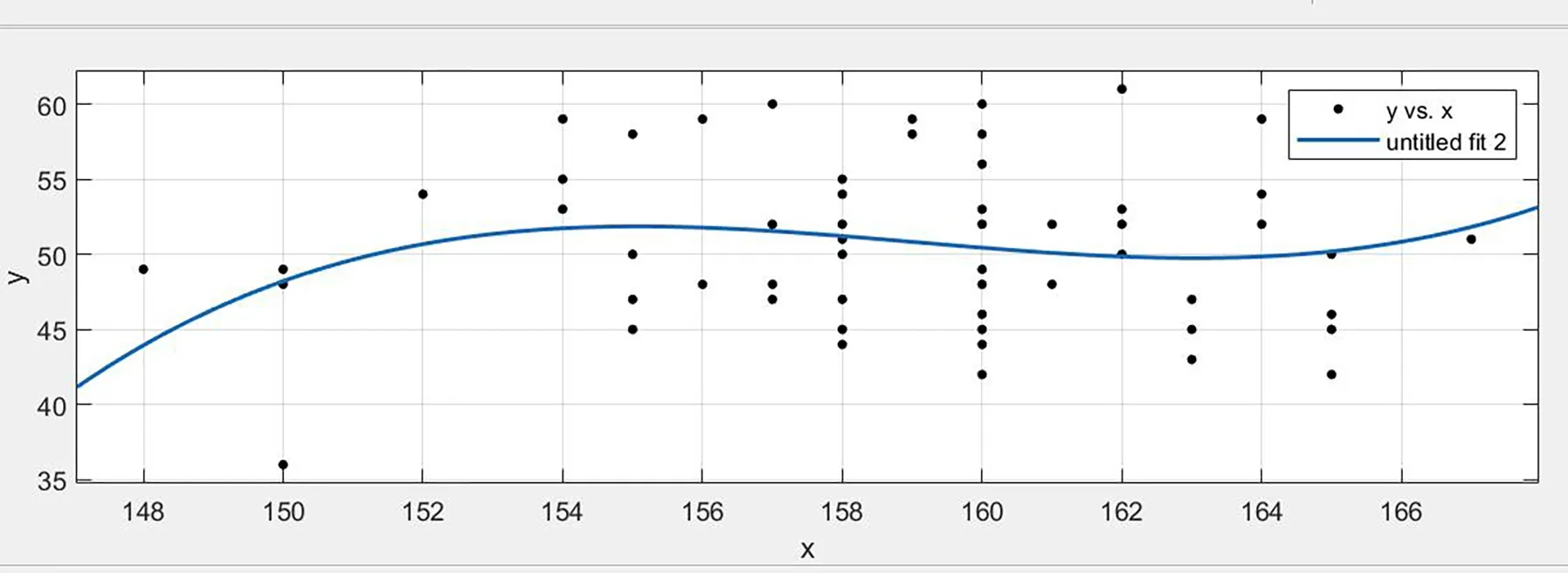
图6

类似于BMI的计算方式，根据学生身高与体重的正弦型拟合函数，计算出每位同学拟合后的体重，接着算出每位同学实际体重与拟合后体重的比值，这个比值如果大于1.2，则表示这位同学偏胖，如果低于0.8，则表示这位同学偏瘦，其他为正常.其分析结果如下：最大比值是1.333，最小比值是0.7128，其中比值为0.7—0.8的有6人，0.8—0.9的有28人，0.9—1.0的有35人，1.0—1.1的有29人，1.1—1.2的有27人，1.2—1.3的有4人，1.3—1.4的有2人，即偏瘦的有6人，其中2名女生、4名男生，偏胖的有6人，全部是男生，其他119人均在正常范围内.

四、研究结果的讨论

在数学建模活动的整个过程中，学生兴趣高涨，有新鲜感，分工明确，计划周详，结果较理想，但是也暴露了一些不足.

1.数学建模思想薄弱，甚至为零

从小学到初中再到高中，考试分数一直都是学生学习的指挥棒.学生虽然接触过数学模型，但是很少有人系统地学习此模块，甚至有的学生连什么是数学建模都不知道.在对50名学生的访谈中，只有3名学生了解数学建模思想，明确分工合作、活动流程等，有10名学生仅限于听说过，甚至有5名学生对此认识为零.

2.动手操作能力不强，学习能力不足，分析能力不高

从组建团队、开展研究活动到撰写研究报告、交流展示，大多数学生处于懵懵懂懂的状态，他们对数据分析仅限于平均值的计算，而对于如何对函数模型进行拟合完全不懂.在学习MATLAB数学软件时，学生的自学能力不足，更缺乏钻研精神.

3.兴趣泛泛，参与度不够

学生对学习数学的目标还停留在学习课堂知识，掌握基础知识，考出好成绩.学生对于这种研究活动缺乏兴趣，其参与度自然不够，全班参加的人数只有8人，只占六分之一.

五、启示与建议

数学建模不仅对实际生活有重大影响，而且在选拔性考试中，数学建模的占分比重越来越大，因此针对以上不足，提出以下几点建议.

1.教师方面

在课堂教学中，教师是学生的引导者，因此在教学建模时，学生想要更好地接受其思想，教师的作用至关重要.对此，教师要在日常的教学过程中，多灌输数学建模思想，关注数学实际应用，开阔数学建模眼界，优化课堂教学过程，提高数学建模能力，同时，完善和补充自身的知识储备，对知识、建模等烂熟于心.再者，建立良好的师生关系，激发学生的积极性，提高学生的参与度，促进学生个人发展.

2.学生方面

首先，在繁重的学习压力下，学生要安排一定时间学习数学建模知识，探究问题的本源和实际应用场景，通过数学建模，洞察现实生活案例，解决生活问题.其次，教师要加强学生之间的团队合作精神.数学建模活动是一个多人合作的项目，由于个人的差异，问题看法角度不同，往往会有不同的答案，这就需要团队的沟通，求同存异.最后，学生要提高信息处理能力.在收集资料过程中，数据庞大，杂乱无章，这就需要学生具有一定的信息处理能力，并且处理数据的过程难免会涉及陌生学科领域，这也就要求学生具有一定的自学能力和综合处理问题的能力.

3.其他方面

在学生学习的过程中，学校能为学生提供一些基础条件，如聘请专家学者开展座谈会，提高学生的学习欲望，定期进行数学建模比赛.同时，家庭和社会也应该给予更多的关注.社会需要的是拥有出色实践能力的复合型人才，这也要求家长和社会对学生的培养更偏重于综合发展.