平均值的一组新不等式
2022-04-13刘小宁
刘小宁
(武汉软件工程职业学院 湖北 武汉:430205)
1 一组优美的平均值不等式
设ai与t为正数,n为不小于2的自然数,当i=1,2,…,n时,记An、Gn与Hn分别为n个正数ai的算术平均值、几何平均值与调和平均值,即
文中构建了如下一组3个结构新颖且形式优美的平均值不等式
(1)
等号当且仅当
时成立。
(2)
等号当且仅当
时成立。
(3)
等号当且仅当
时成立。
实际上,平均值不等式(1)~(3)也是3个关于正数ai个数n的单调递增函数。
在算术平均值An,几何平均值Gn与调和平均值Hn之间,还存在大家熟悉的算术——几何——调和平均值不等式[1]
An≥Gn≥Hn
(4)
等号当且仅当a1=a2=…=an时成立。
式(1)~式(3)是含参数t的平均值不等式,而平均值不等式(4)不含参数t。
2 证明
为证明结构新颖且形式优美的平均值不等式(1)~(3),先证明如下定理。
定理:若x与t为正数,则
(5)
等号当且仅当t=xn-1时成立。
证明:设y与m为正数,作辅助函数
R(y)=yn-n·mn-1·y+(n-1)·mn
则
由于y与m为正数,
1)若y=m,则R(y)=0;
2)若x 则 3)若y>m,有y-m>0,且 故 以上分析表明,当y与m为正数时,恒有 R(y)=yn-n·mn-1·y+(n-1)·mn≥0 在上式中作变换 可得到定理即式(5),等号当且仅当y=m即t=xn-1时成立。定理证毕。 不等式(1)的证明:令定理中 注意到 不等式(2)的证明:令定理中 注意到 不等式(3)的证明:令定理中 注意到 以及 an=n·An-(n-1)·An-1 不等式(4)的证明:取不等式(1)中t=1,可得算术——几何平均值不等式:An≥Gn;取不等式(2)中t=1,可得几何——调和平均值不等式:Gn≥Hn;综合这两个不等式,可得到算术——几何——调和平均值不等式(4),等号当且仅当a1=a2=…=an时成立。不等式(4)证毕。 例1:记关于n个正数ai的算术平均值An,几何平均值Gn与调和平均值Hn的均差函数分别为 F1(n)=n(An-Gn) (6) (7) F3(n)=n(An-Hn) (8) 则F1(n),F2(n)与F3(n)分别是n的单调递增函数。 证明:取不等式(1)~(3)中t=1,可分别得到 F1(n)≥F1(n-1) F2(n)≥F2(n-1) F3(n)≥F3(n-1) 故F1(n),F2(n)与F3(n)分别是n的递增函数。 因为例1中关于式(6)为递增函数的结论是Rado不等式[2-6],所以式(7)与式(8)为递增函数的结论可视为Rado不等式的推广[7]。 例2:记关于n个正数ai的算术平均值An,几何平均值Gn与调和平均值Hn的均商函数分别为 (9) (10) (11) 则f1(n),f2(n)与f3(n)分别是n的单调递增函数。 证明:1)取不等式(1)中 整理可得到:f1(n)≥f1(n-1) 故例2中式(9)是n的单调递增函数。 2)取不等式(2)中 整理可得到:f2(n)≥f2(n-1) 故例2中式(10)是n的单调递增函数。 3)取不等式(3)中 整理可得t到:f3(n)≥f3(n-1) 故例2中式(11)是n的单调递增函数。 因为例2中关于式(9)为递增函数的结论是Popovic不等式[2-6],所以式(10)与式(11)为递增函数的结论可视为Popovic不等式的推广[7]。 例3:设r为不超过n的正整数,即r=1,…,n时,则 An≥q1(r)·Gn≥Gn≥q2(r)·Hn≥Hn An≥q3(r)·Hn (12) 其中 (13) 证明:当r为非负整数且r=1,…,n时, 1)因为例2中式(9)是单调递增函数,有 由算术——几何平均值不等式即不等式(4)的最左项与中间项,可知式(12)中第一式的最左项与中间项,以及式(13)的q1(r)成立。 2)因为例2中式(10)是单调递增函数,有 由几何——调和平均值不等式即不等式(4)中的中间项与最左右项,可知式(12)第一式的中间项与最左项,以及式(13)的q2(r)成立。 3)因为例2中式(11)是单调递增函数,有 由算术——几何——调和平均值不等式即不等式(4)的最左项与最右项,可知式(12)中第二式,以及式(13)的q3(r)成立。 例3表明,在n个正数ai的算术平均值An与几何平均值Gn之间,以及在几何平均值Gn与调和平均值Hn之间可分别加细,例3中的q1(r)与q2(r),分别是An与Gn之间,Gn与Hn之间的加细系数;在An与Hn之间,可用系数q3(r)进行加细。 根据式(6)与式(7)递增性的证明过程,可得到 例4:设r为不超过n的正整数,且r=1,…,n-2时,则 显然,例4是算术——几何——调和平均值不等式加细的又一种形式。
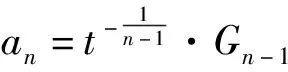
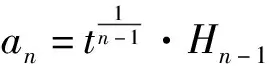
3 应用
