信息系统中的相对知识距离及其认知特征

2022-07-25王宝丽韩素青廉侃超林国平

渤海大学学报（自然科学版） 2022年1期

王涛，王宝丽*，，，韩素青，廉侃超，林国平

(1．太原师范学院数学系，山西晋中030619；2．运城学院数学与信息技术学院，山西运城044000；3．闽南师范大学数学与统计学院，福建漳州363000)

0 引言

波兰数学家Zdzislaw Pawlak提出的Rough Sets理论对论域进行划分，构成粒度求解的最基本的结构，这种划分结构亦称为知识[1-2]．知识的不确定性度量在知识获取中发挥着重要的作用[3]，研究者从不同的角度出发，提出了许多不同种类的不确定性度量方式，如知识粒度、知识粗糙熵、知识条件熵、知识距离等．知识距离作为其中一种基础性度量，能够从数量上反应不同结构之间的量化差异．王宝丽等[4]首先提出知识距离的概念，并从内涵、构造以及多粒度应用等方面进行了深入地研究，取得了一些有意义的结果．Qian等[5-7]进一步研究了精确知识和模糊知识的知识结构、知识粒度的不变性以及知识距离对粒度的刻画，解释了知识距离在人类变粒度求解中的重要作用．Liang等[8]基于知识距离对粗糙集中包含度，近似精度，粗糙度等进行了距离视角的解释．

近年来，知识距离的研究成果更加丰富．为了刻画知识结构，Qian等[9]基于知识距离对划分粒结构进行聚类，分析了粒结构聚类中体现的聚集性和收敛性，并对人类粒选择的行为进行模拟仿真．Yang等[10]对集合距离与知识距离构建代数格，研究了粒结构的三个层次．为了丰富知识距离的表达形式，Chen等[11]运用Jaccard距离替代集合相似度，给出了新的知识距离的度量公式，并将信息系统中的划分知识距离推广到邻域信息系统中，丰富了知识距离的含义，为知识距离在机器学习领域的应用提供了新思路[12]．在此基础上，Yang等从物流分配优化角度证明了只要给出粒之间的距离，便可通过组合的方式构造知识距离[13-15]．Dai等讨论了集值信息系统下的熵与粒度度量，从高斯核的视角研究了模糊信息系统下的不确定性度量，提出了模糊结构差异的信息度量，并研究了直觉模糊粒结构距离[16-18]．Li等[19]则进一步提出了一组区间值直觉模糊集描述下的模糊粒结构距离，证明了知识距离是直觉模糊粒结构距离的特殊形式．

值得关注的一点是，上述所有研究都只从不同的角度给出了两个知识的绝对差异性度量，均未描述和分析任意条件下两个知识的差异，即知识的相对差异性度量．事实上，人类认识事物总是从已有的知识出发，通过分析知识空间中知识差异性来获取新知识，而知识的差异性应该与观察者所拥有的先验知识或观察视角相关．拥有的先验知识不同或所处的角度不同，知识的差异性也应当有所不同．杨洁等[20]提出一种带近似描述能力的邻域信息粒距离，用来反映不同邻域知识空间对目标概念的刻画能力的差异性，但这一研究仍无法描述不同认知视角对知识差异的影响．为了解决以上问题，本文在具备一定先验知识的条件下研究两个知识空间之间的距离及其在知识获取方面的认知特征，从而反映知识之间的相对认知差异．

本文第1节简要介绍相关基本概念；第2节提出了相对知识距离的概念，分析了相对知识距离的保序性、有界性及条件依赖性，并证明绝对知识距离是相对知识距离的特殊情形；为了刻画人类多粒度认知的特性，本文在第3节以实验方式呈现相对知识距离与绝对知识距离所具有的不同的结构信息，同时基于相对知识距离提出一种新的特征选择算法，用以分析在不同先验知识条件下的特征选择所呈现的人类认知变化特性；第4节总结全文．

1 信息系统与知识距离

1．1 信息系统及知识表示

定义1：四元组S=(U，A，V，f)是一个信息系统，其中U={x1，x2，…，xn}为对象的非空有限集，称为论域；A为属性的非空有限集；V=∪a∈AVa是属性值的集合，Va表示属性a的值域；f：U×A→V表示一个信息函数．

对于每个属性子集P⊆A，定义论域U上的一个二元不可分辨关系：

IND(P)={(x，y)∈U×U|∀a∈P，fa(x)=fa(y)}

(1)

显然，IND(P)是一个等价关系，因此IND(P)可诱导得到论域U的一个划分，记为U/IND(P)，简记为U/P．从粒计算的观点来看，U/P中的每个等价类都可以视为一个知识颗粒，表示为U/P={[xi]P|xi∈U}．在粗糙集理论中，将知识粒的集合U/P称为论域U的一个知识，为了方便分析与说明，下文中将其称为知识P．

在论域U上的所有知识构成的知识库中，恒等关系ω对应最细的知识，全域关系δ对应最粗的知识．

定义2[4]：设U为非空有限论域，P和Q为U上的两个知识，若对∀xi∈U，满足[xi]P⊆[xi]Q，则称知识P比知识Q更精细，记为P⪯Q．

1．2 知识距离

定义3[5-6]：设U为非空有限论域，P和Q为U上的两个知识，P与Q之间的知识距离定义为

(2)

其中[xi]p⊕[xi]q=([xi]p∪[xi]q)-([xi]p∩[xi]q)．

例1：给定论域U={x1，x2，x3，x4，x5，x6}上的两个知识，P={{x1，x3}，{x2，x6}，{x4，x5}}，Q={{x1，x3，x5，x6}，{x2，x4}}．知识P与Q之间的知识距离为d(P，Q)=4/9．

以上的知识距离度量反映了两个知识之间的绝对差异，但与观察者所拥有的先验知识或所处的角度无关，不能反映在先验知识或条件认知下的知识之间相对认知差异．因此本文提出了基于不同认知视角或认知条件下的相对知识距离，进而反映人类多粒度相对认知的特点．为与下文给出的距离定义相区别，将第1．2节中所述的知识距离称为绝对知识距离．

2 相对知识距离

本节提出相对知识距离的概念并分析其性质．

定义4：U为非空有限论域，R为U上的先验知识或条件认知，知识P和Q在R下的相对知识距离定义为

(3)

该定义将对先验知识或条件认知R的相对描述融入到已有的知识距离公式中，以反映在不同认知视角下任意两个知识P和Q的相对差异性．定义4也称为P和Q关于R的相对知识距离．

下面分析相对知识距离D(P，Q|R)所具有的性质．

性质1：设U是一个非空有限论域，P1，P2，P3为U上的知识，R为U上的先验知识或条件认知，则相对知识距离D满足：

(1)非负性D(P1，P2|R)≥0；

(2)对称性D(P1，P2|R)=D(P2，P1|R)；

(3)三角不等式D(P1，P2|R)+D(P2，P3|R)≥D(P1，P3|R)．

证明：性质(1)(2)显然成立，下证(3)成立．

欲证知识P1，P2，P3关于R的相对知识距离满足三角不等式，根据定义，只需证|([xi]P1∩[xi]R)⊕([xi]P3∩[xi]R)|≤|([xi]P1∩[xi]R)⊕([xi]P2∩[xi]R)|+|([xi]P2∩[xi]R)⊕([xi]P3∩[xi]R)|，即证|([xi]P1⊕[xi]P3)∩[xi]R|≤|([xi]P1⊕[xi]P2)∩[xi]R|+|([xi]P2⊕[xi]P3)∩[xi]R|．

性质1表明，论域U的条件知识关于相对知识距离D(P，Q|R)构成一个度量空间．

例2：给定论域U={x1，x2，x3，x4，x5，x6}上两个需区分的知识P={{x1，x3}，{x2，x6}，{x4，x5}}，Q={{x1，x3，x5，x6}，{x2，x4}}，在先验知识R1={{x3，x6}，{x1，x2，x4，x5}}，R2={{x1，x2，x5}，{x3，x4，x6}}下，知识P和Q的相对知识距离为：D(P，Q|R1)=1/36×(1+1+1+2+2+1)=2/9，D(P，Q|R2)=1/36×(1+0+1+0+1+1)=1/9．

从例1和例2可知，知识P和Q在不同的先验知识或条件认知下的相对知识距离是不同的，相比于例1中计算出的知识P和Q之间的绝对知识距离，例2中计算出的相对知识距离更小．

性质2：设U是一个非空有限论域，P1，P2，P3为U上的知识，R为U上的先验知识或条件认知，若序关系P1⪯P2⪯P3成立，则

D(P1，P2|R)+D(P2，P3|R)=D(P1，P3|R)

(4)

故D(P1，P2|R)+D(P2，P3|R)=D(P1，P3|R)．

性质2体现了在相同先验知识或条件认知下，相对知识距离保持了序关系下等式成立的性质．

性质3：设U是一个非空有限论域，P和Q为U上的知识，R1和R2为U上的先验知识或条件认知，若知识R1和R2满足序关系R1⪯R2，则

D(P，Q|R1)≤D(P，Q|R2)

(5)

设任意对象xi∈([xi]P⊕[xi]Q)∩[xi]R1，则有xi∈[xi]R1且xi∈([xi]P⊕[xi]Q)，又[xi]R1⊆[xi]R2，所以xi∈[xi]R2，进而xi∈([xi]P⊕[xi]Q)∩[xi]R2，(([xi]P⊕[xi]Q)∩[xi]R1)⊆(([xi]P⊕[xi]Q)∩[xi]R2)．由此知D(P，Q|R1)≤D(P，Q|R2)成立．

从性质3可以看出，随着先验知识或条件认知的不断细化，知识之间的相对知识距离在单调下降．这一规律反映了在渐进认知过程中，随着已有认知水平的不断提高，可以逐渐降低两个知识之间的相对认知难度，体现了人类多粒度渐进认知的特性．

推论1：设U是一个非空有限论域，当R是U上最粗的知识δ时，有D(P，Q|δ)=d(P，Q)．

证明：根据公式(3)，有

推论1说明了绝对知识距离是两个知识之间在没有任何认知前提下的差异性度量，因此绝对知识距离是相对知识距离的一个特例．

推论2：设U是一个非空有限论域，当R是U上最细的知识ω时，知识P与Q之间的相对知识距离D(P，Q|R)达到最小值0．

证明：若先验知识或条件认知R是U上最细的知识，即R=ω，则P与Q之间的相对知识距离为

根据性质3，对于U上的任意知识R，若满足序关系ω⪯R⪯δ，则不等式D(P，Q|ω)≤D(P，Q|R)≤D(P，Q|δ)成立，即相对知识距离满足：0≤D(P，Q)≤d(P，Q)．

例3：给定论域U={x1，x2，x3，x4，x5，x6}上的知识P={{x1，x3}，{x2，x6}，{x4，x5}}，Q={{x3，x4，x5}，{x1}，{x2}，{x6}}，U上的先验知识为R={{x3，x6}，{x1，x2，x4，x5}}，知识P和Q关于知识R的相对知识距离为D(P，Q|R)=1/36×(0+0+0+0+0+0)=0．

例3表明，R=ω仅仅是D(P，Q|R)=0成立的充分条件，但非必要条件．

性质4：设U是一个非空有限论域，U上的知识P和Q之间存在如下条件依赖关系：

D(P，Q|P)+D(P，Q|Q)=d(P，Q)

(6)

证明：

性质4说明了P与Q之间的绝对知识距离可以分解为不同方向的单向相对知识距离之和，即从P到Q的认知难度与从Q到P的认知难度之和，进而从理论上解释了相对知识距离与绝对知识距离的辩证统一性．

3 数据实验

本小节将从实验上分析相对知识距离与绝对知识距离在实际问题的结构差异；此外，通过设计基于相对知识距离的特征选择算法，研究相对知识距离在知识获取与发现中的认知特征．

3．1 绝对知识距离与相对知识距离的结构差异性

对于给定的对象集，不同的距离计算方法，可以得到不同的分层结构．谱系聚类法是一种基于对象集上的距离矩阵，通过定义类与类之间的距离，依次将最近的类进行合并形成分层递阶结构的聚类方法[21]．这里运用相同的谱系聚类算法得到不同的聚类结构来显示本文所提距离与经典绝对知识距离的差异，进一步证实相对知识距离可以为知识获取提供与绝对知识距离不一样的视角．实验流程如下：

已知在信息系统S=(U，A，V，f)中，A={a1，a2，…，am}为S中的条件属性集，对于条件属性集A中的每个属性进行如下的计算：

(1)对∀ak∈A，k={1，2，…，m}，通过等价关系可得ak诱导的知识Pk，并将其作为先验知识或条件认知Rk；

(2)计算由其余属性诱导的知识在Rk作为条件认知的相对知识距离Dij(Pi，Pj|Rk)和绝对知识距离dij(Pi，Pj)，并得到相对知识距离矩阵M=(Dij)和绝对知识距离矩阵N=(dij)；

(3)基于两个距离矩阵M和N，分别用谱系聚类法对数据集的属性子集进行聚类，得到不同的聚类结构；

(4)分别以知识粒度[6]之差ΔGK(X)和知识距离d(P，Q)作为度量标准，计算聚类结果的差异性．其中，

(7)

下面以UCI数据库中的Zoo数据集和Las Vegas Trip Advisor Reviews(简称Las Vegas)数据集为例，并分别以数据集中的属性a1和属性a5诱导的知识作为条件知识R，构造相对知识距离和绝对知识距离矩阵，进行属性集聚类，聚类结果见图1和图2．(图中Rel-a1表示以a1作为条件属性的相对知识距离的聚类，Abs-a1表示去掉a1以后基于绝对知识距离的聚类)

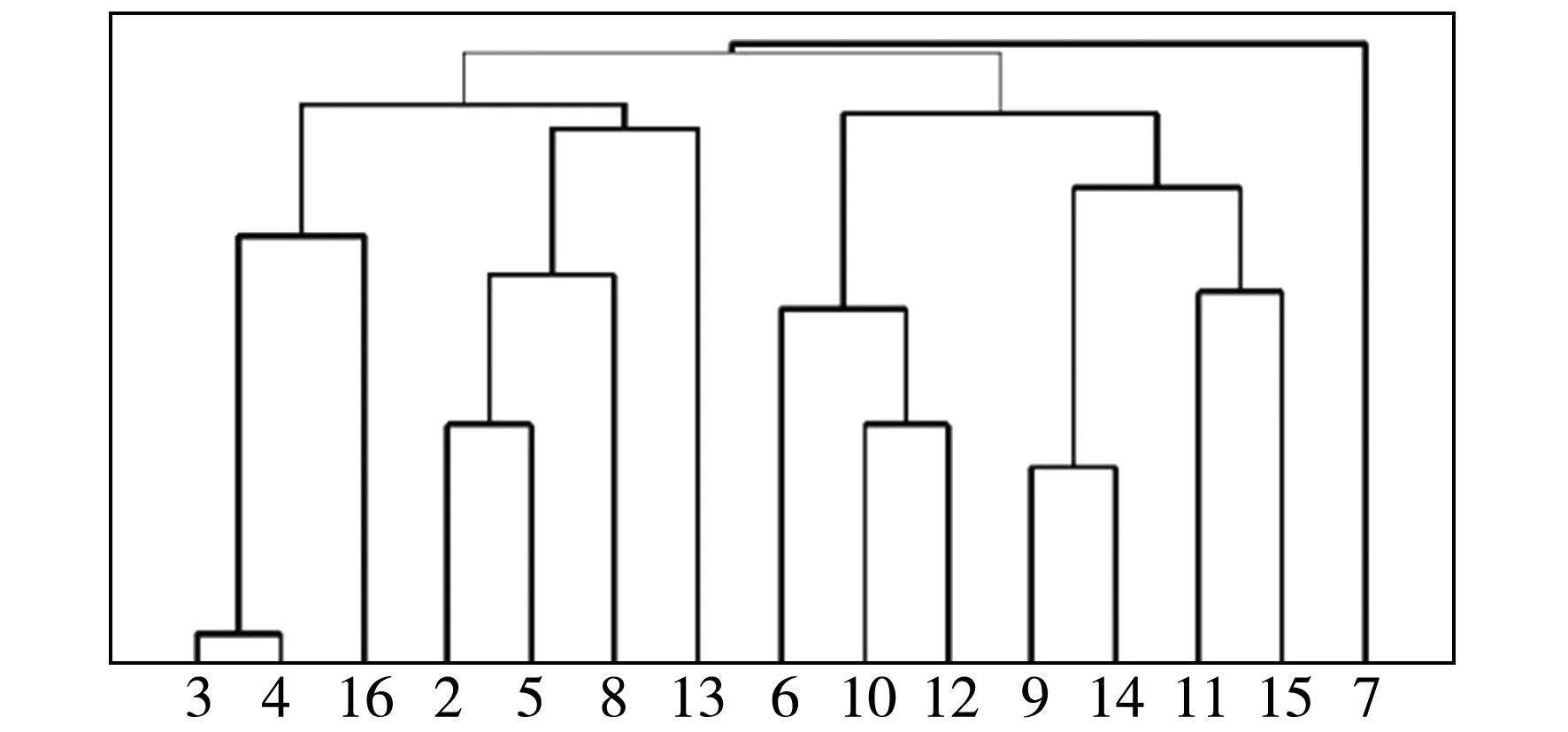
(a)Abs-a1

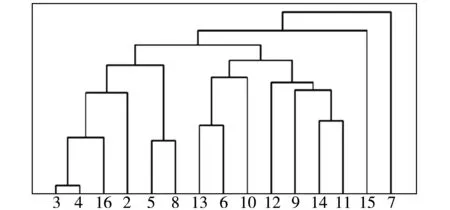
(b)Rel-a1

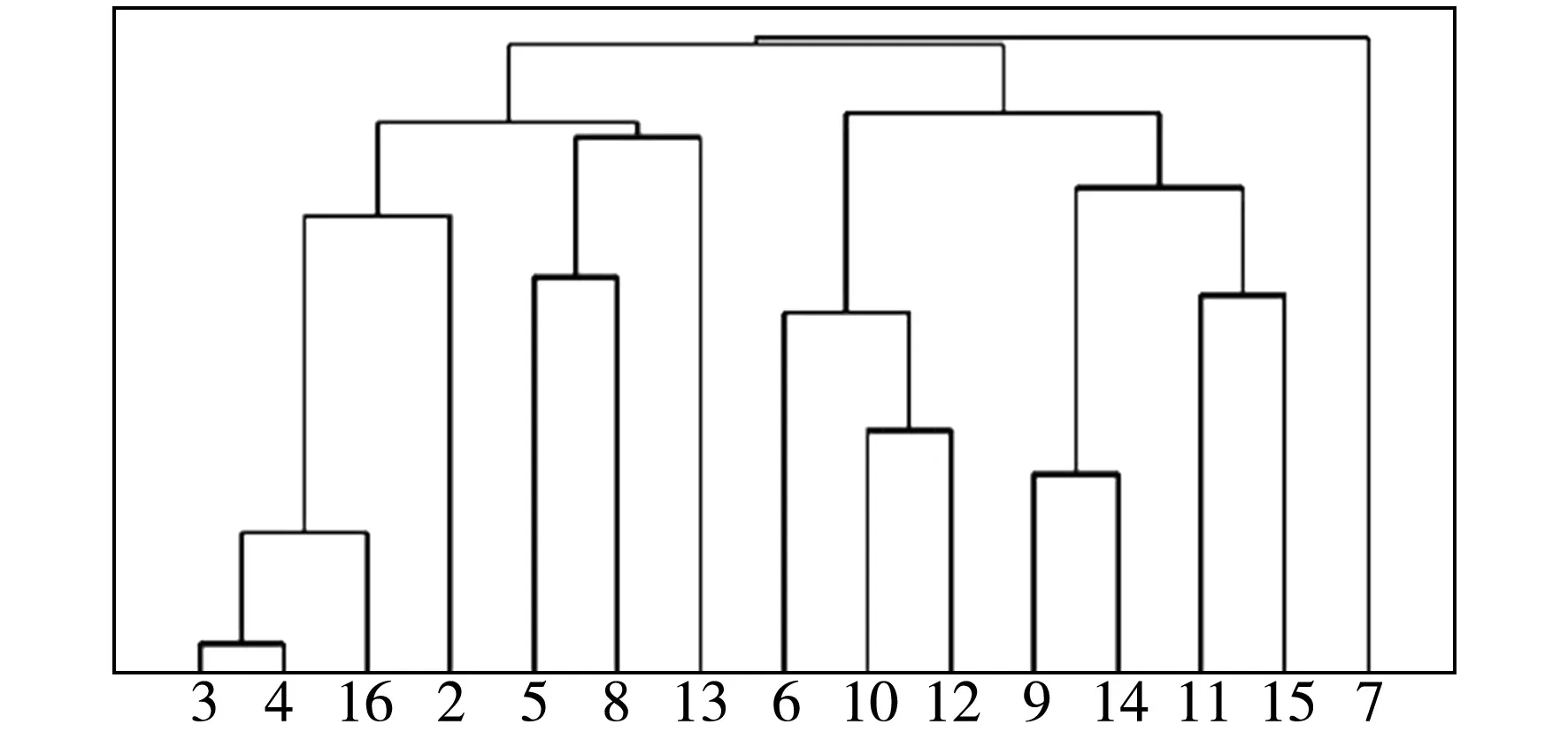
(c)Abs-a5

(d)Rel-a5

(a)Abs-a1

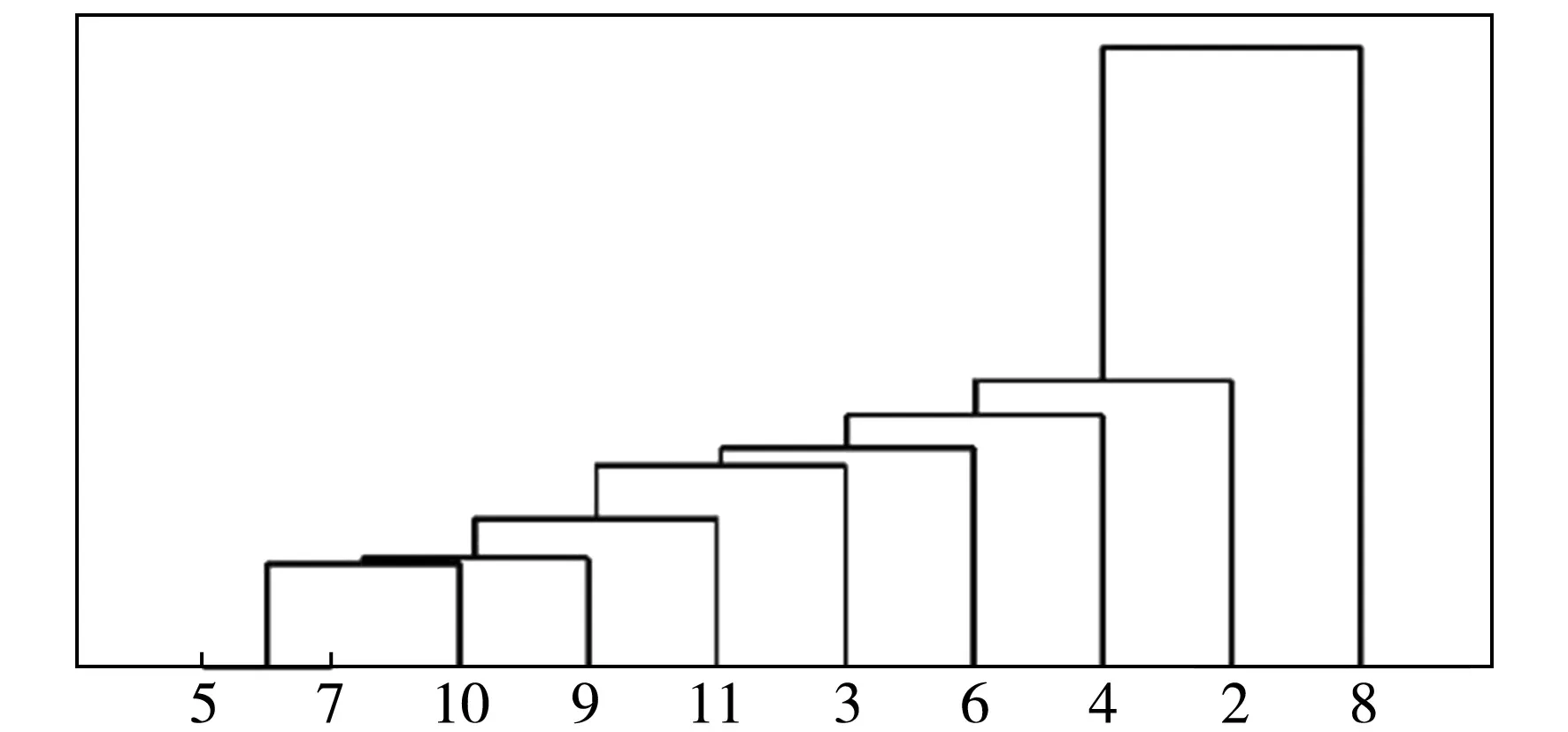
(b)Rel-a1

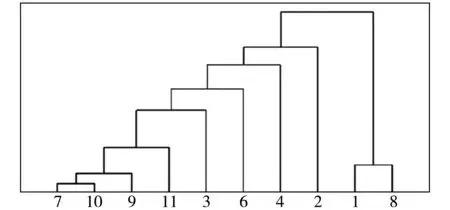
(c)Abs-a5

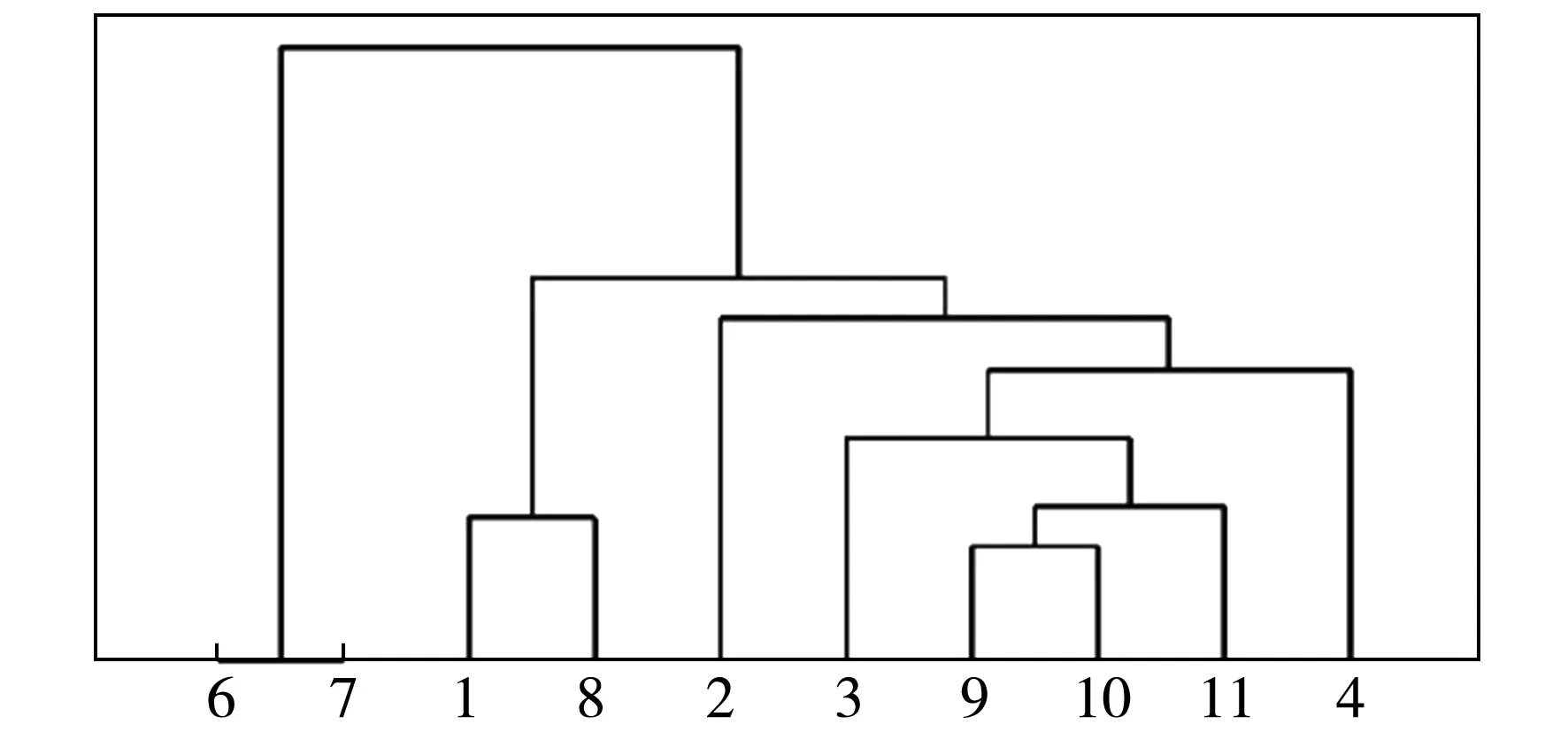
(d)Rel-a5

为了更直观地描述聚类结果的差异，本文计算了在不同的分类个数下，基于绝对知识距离的谱系聚类和基于相对知识距离的谱系聚类的数值差异，结果见图3和图4．

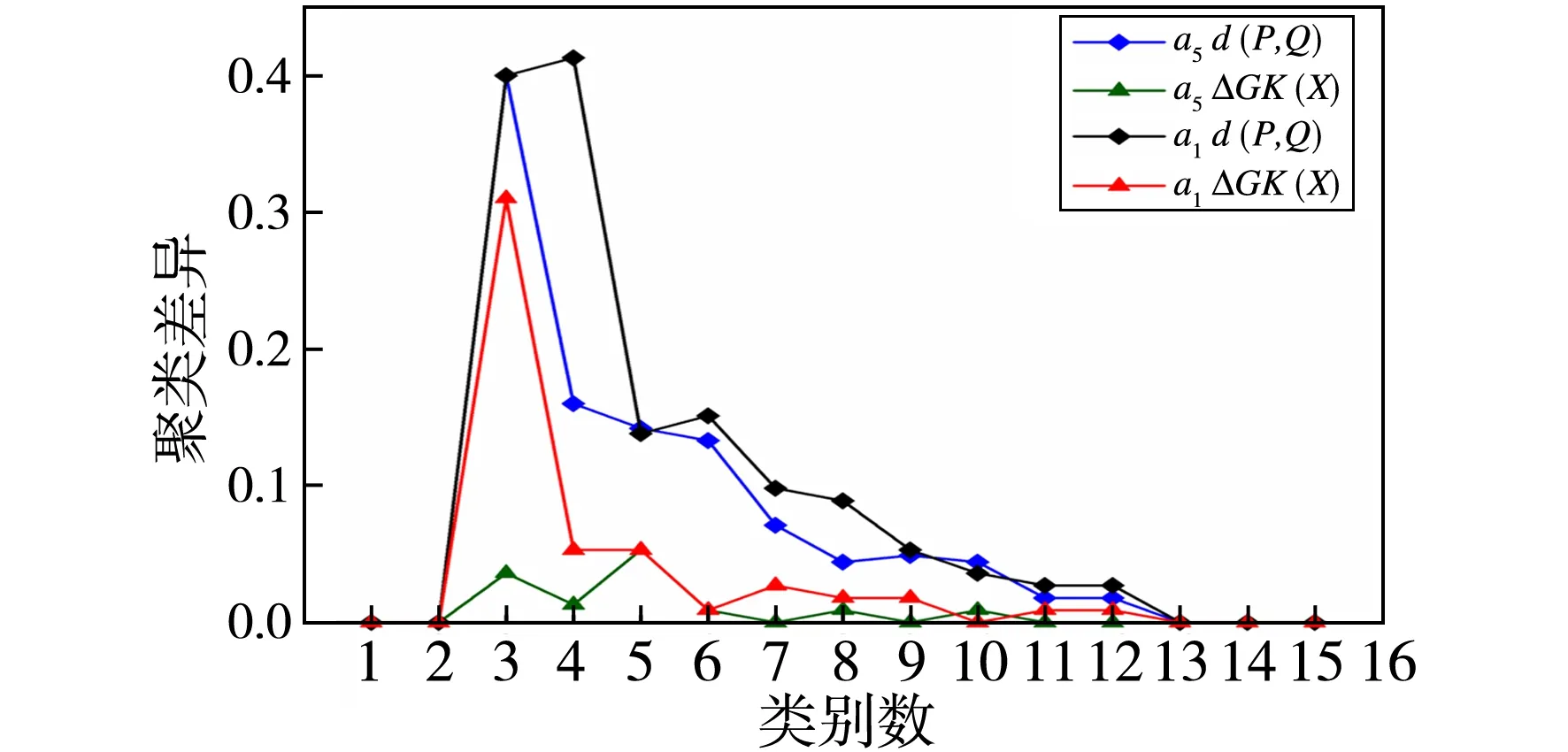
图3 Zoo数据集中相对知识距离和绝对知识距离关于不同类别数的聚类差异

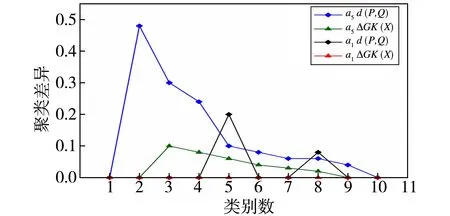
图4 Las Vegas数据集中相对知识距离和绝对知识距离关于不同类别数的聚类差异

以上实验对比结果表明，基于相对知识距离的谱系聚类和基于绝对知识距离的谱系聚类在不同的分类个数下具有明显差异，具体表现为：

(1)当相同属性作为条件属性时，基于相对知识距离和基于绝对知识距离的谱系聚类结构是有差异的；

(2)当不同属性作为条件属性时，基于相对知识距离和基于绝对知识距离的谱系聚类结构的差异是不同的；

(3)在不同的类别数下且条件属性不同时，基于相对知识距离和基于绝对知识距离的谱系聚类结构的差异是不同的．

因此，相对知识距离与绝对知识距离在实际应用中存在着明显的差异，相对知识距离具有更为丰富的信息特性，可以对人类不同认知视角认知事物结构进行有效建模．

3．2 基于相对知识距离的特征选择算法

特征选择是一类重要的数据预处理方法，目的是从数据集的特征集合中选出对学习任务有用的相关特征子集[24]．在特征选择过程中，是否存在先验知识所选出的特征子集可能有所不同．

例如，考虑立方体对象，若已有特征为底面长l、底面宽w、底面积S、高h、密度ρ和颜色c等6个特征，在执行描述立方体质量的特征选择任务时，若从先验特征S出发，则选出的特征子集是S，h，ρ，而没有先验特征时，选出的特征子集可以是l，w，h，ρ．因此，有必要根据不同的机制，分析先验特征对特征选择结果的影响．

本节设计了过滤式的特征选择方法，并以相对知识距离作为评价函数．算法求解思想如下：

在子集搜索过程中，依照前向搜索策略，将特征集合{a1，a2，…，am}中的每个特征作为候选单特征子集，根据定义4中的相对知识距离，依次加入到候选子集中，直到满足停止条件；

在子集评价过程中，将候选子集中与原来系统中相对于知识R的距离为0的特征剔除，最终得到系统的特征子集．

算法1：基于相对知识距离的特征选择算法

输入：信息系统S=(U，A，V，f)，初始状态的知识R

输出：特征子集I

Step1 初始化候选子集F=∅，I=∅，

对∀a∈A，IfD(A{a}，A|R)≠0

ThenF=F∪{a}；

Step2 令I′=F；

Step3 IfD(I′，A|R)=0转到Step7，否则执行Step4；

Step4 ∀a∈AI′，计算D(I′∪{a}，A|R)，选择使D(I′∪{a}，A|R)最大的属性a′；

Step5I′=I′∪{a′}；

Step6 WhileI′≠A，返回Step3；

Step7 对∀a∈I′，ifD(I′{a}，A|R)=0

ThenI=I′{a}；

Step8 输出信息系统S的特征子集I，算法结束．

实验分析

本节将基于相对知识距离的特征选择算法与基于绝对知识距离的特征选择算法进行比较，以进一步说明不同的距离度量对信息系统的认知差异．实验选用UCI数据库中的6个数据集，以相对知识距离作为评价准则进行特征选择，并将在3．1节的实验中聚类差异最大的特征所诱导的划分知识作为先验知识或条件知识，实验结果见表1．

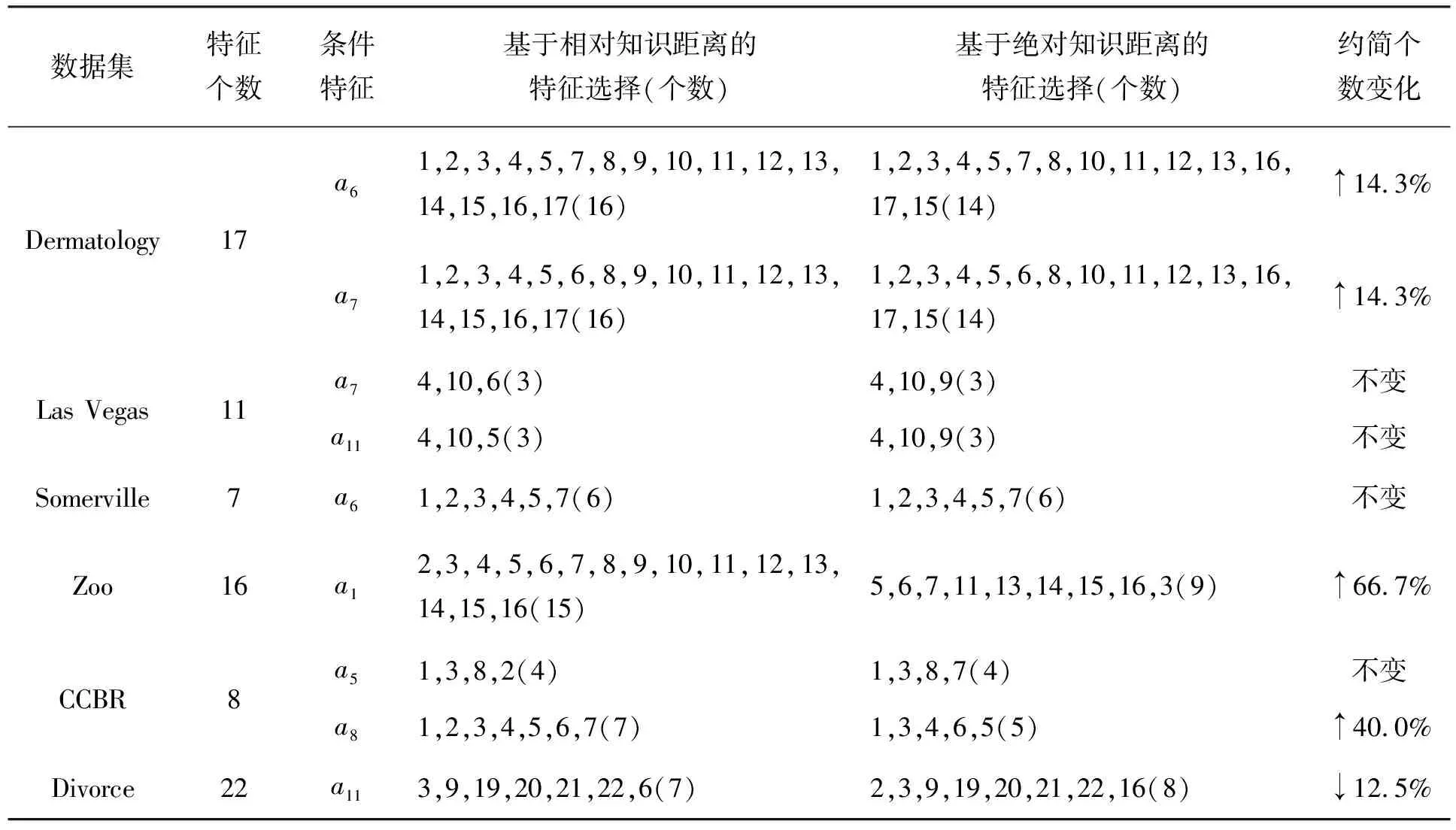
表1 基于两类距离算法在6类数据集下的特征选择结果

实验结果表明，对信息系统采用不同的知识距离得到的特征选择结果具有一定的差异．这种差异来源于不同的度量机制，由于将系统中的部分特征作为先验知识或条件知识，导致对系统的认知路径发生改变，因此获得了不同的特征选择结果．

此外，分析两种特征选择算法中特征个数的变化，我们可以得到以下结论：

(1)当先验特征有利于描述信息系统整体性能时，对系统的认知能力有所增强，较少的特征就能达到信息系统全部特征所具备的分类能力，因此本文算法输出的特征个数少于对比算法中的特征个数；

(2)当先验特征所蕴含的信息量较少、对信息系统的认知能力有所减弱时，需要较多的特征才能刻画系统的分类能力，因此本文算法输出的特征个数多于对比算法中的特征个数；

(3)当先验特征对描述信息系统整体性能无影响时，保持了对信息系统的认知能力，因此本文算法输出的特征个数与对比算法中的特征个数相等．

4 结论

本文从相对认知视角出发研究了知识空间的相对性差异．具体地，提出相对知识距离的概念，分析了相对知识距离具有的认知特性，通过属性聚类实验说明了相对知识距离较于绝对知识距离所具有的不同的结构特性．此外，基于相对知识距离的特征选择算法也对人类条件渐进认知增强、保持与减弱特性进行了模拟与仿真．本文主要结论有：

(1)相对知识距离反映了不同视角下任意两个知识之间的相对差异性，体现了人类多粒度相对认知的特性；

(2)相对知识距离比绝对知识距离更具有一般性，在已知先验知识或条件认知的前提下，相对知识距离可以降低两个知识之间的认知难度，符合一般的认知规律；

(3)相对知识距离与绝对知识距离具有不同的拓扑结构，且由于度量机制的不同，对系统的认知路径也会有所改变，可以为人类多视角认知提供有效参考．

本研究进一步丰富了粒计算的不确定性度量理论，为现实信息系统的认识刻画提供了新的视角．相对知识距离在邻域、模糊信息系统以及各类决策系统中的应用将是我们下一步的研究方向．