基于单边微腔量子点耦合系统的极化纠缠浓缩
2022-07-25莫晓成杨子龙刘思彤修晓明
董 莉,莫晓成,杨子龙,刘思彤,吕 柳,修晓明
(渤海大学 物理科学与技术学院,辽宁 锦州121013)
0 引言
量子信息是量子力学与信息科学交叉的新兴学科,量子信息同经典信息相比具有潜在的巨大优势.量子通信被证明在原理上是绝对安全的,量子计算机的并行计算能力远远大于经典计算机[1].量子纠缠是量子系统中特有的现象,是完成量子信息处理任务的重要资源[2].然而,在量子系统里,由于环境噪声的存在,使得量子态很容易发生退相干,导致量子态由最大纠缠态演化为非最大纠缠态.这会严重影响完成量子信息处理任务的质量,甚至会对量子信息任务的安全造成威胁.
为了保证完成量子信息处理任务的可靠性和安全性,人们思考各种办法来获得高纠缠度的量子纠缠态,减少环境噪声的影响,纠缠浓缩方案也就应运而生.
纠缠浓缩可以从纠缠度较低的纠缠态中提取出纠缠度较高的纠缠态,甚至是最大纠缠态.1996年,Bennett等基于Schmidt投影测量的方法提出了第一个纠缠浓缩方案[3],此方案是针对Bell类非最大纠缠态|φ〉=α|00〉+β|11〉的纠缠浓缩,要求两个参与者在执行浓缩方案之前已知纠缠态的叠加系数α与β,根据系数设计投影测量.Bose推广了Bennett的纠缠浓缩思想,提出了基于纠缠交换的Bell类非最大纠缠态的纠缠浓缩方案[4],由于纠缠交换的特点,非最大纠缠态的叠加系数对于两个参与者可以是未知的.2000年,Bandyopadhyay提出基于辅助量子比特和一个已知系数Bell类非最大纠缠态的纠缠浓缩方案[5].之后,针对不同纠缠态和不同物理系统的纠缠浓缩方案相继被提出[6-16].2001年,Zhao[6]和Yamamoto等[7]分别利用极化分束器(PBS)等线性光学元件代替Schmidt投影测量,提出了基于线性光学元件的纠缠浓缩方案.2008年,Sheng等利用Kerr非线性介质提出了一个更高效的纠缠浓缩方案[8],方案基于Kerr非线性介质提供的光子之间的非线性相互作用,实现非破坏测量和循环纠缠浓缩过程,从而达到提高成功率的目的.2012年,Sheng等又将PBS线性光学元件和Kerr非线性介质分别引入到已知系数Bell类非最大纠缠态的纠缠浓缩方案,提出了两个借助单辅助量子比特实现的光学系统中已知系数Bell类非最大纠缠态的纠缠浓缩方案[9].
除Kerr非线性介质之外,光学微腔与量子点耦合系统也可以实现光子与光子、电子与电子或光子与电子之间的非线性相互作用[17-22].2014年,Ren和Long利用单边光学微腔量子点耦合系统实现了Bell类超纠缠态的纠缠浓缩[21].2017年,Zhao等利用双边光学微腔量子点耦合系统实现了Bell类纠缠态的纠缠浓缩[22].
本文基于单边微腔与量子点耦合系统,提出两个Bell类纠缠态的极化纠缠浓缩方案.一个是未知系数非最大纠缠Bell态极化纠缠浓缩方案,另一个是已知系数非最大纠缠Bell态极化纠缠浓缩方案.
1 单边微腔与量子点耦合系统
量子点结构特殊,它的形状和大小都是可以人为改变的,其能级结构也可以同时改变,为更好地实现量子比特提供了更多可供选择的方法.

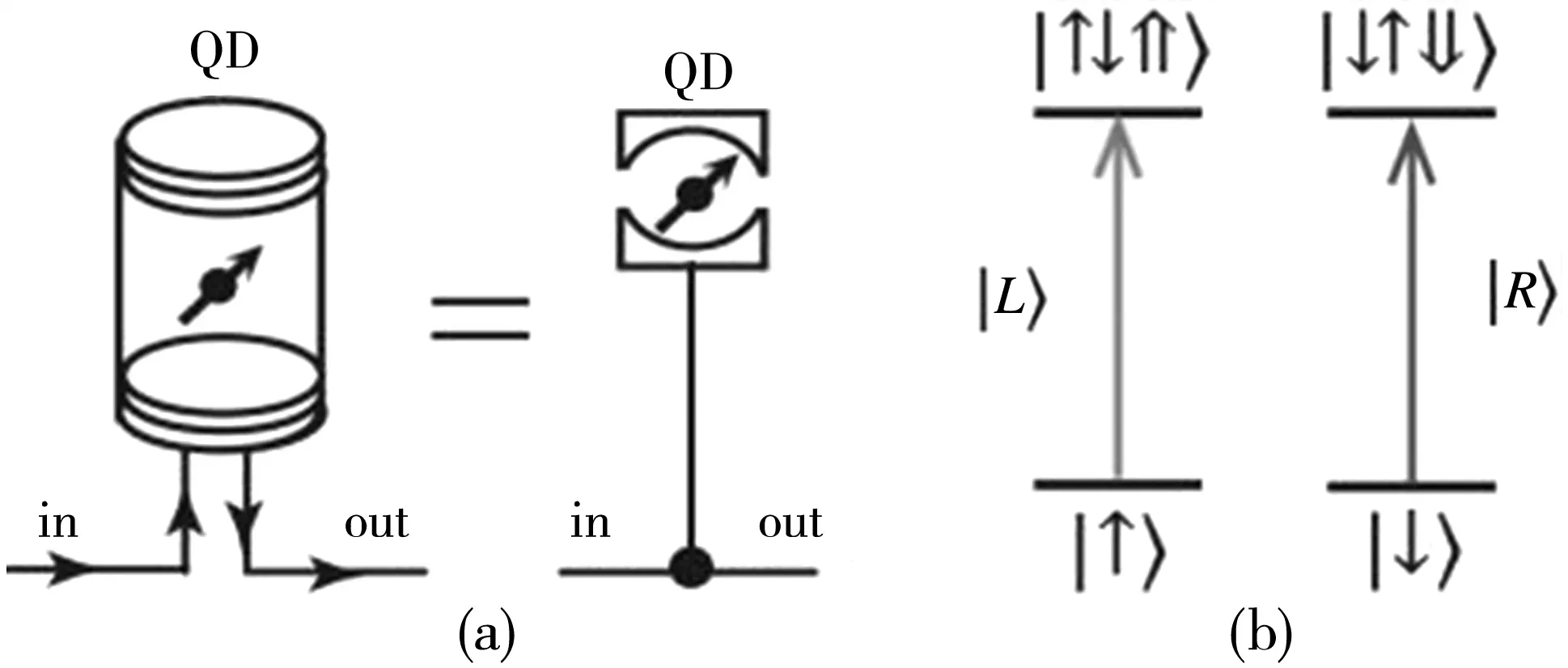
图1 (a)单边微腔与量子点耦合系统的装置结构示意图;(b)耦合系统的能级结构示意图
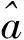
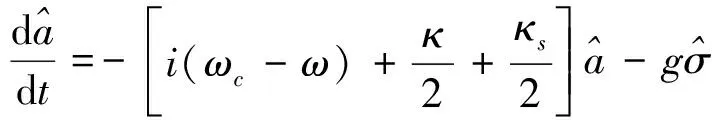
(1)

(2)
(3)

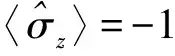
(4)
当g=0,也就是量子点与单边光学微腔不耦合的冷腔,其反射系数为
(5)
在ω=ωX-=ωc,κ>>κs,g>>κ,γ的条件下,热腔和冷腔的反射系数分别为rh(ω)≈1,r0(ω)≈-1,由此可以得到单边量子点光学微腔系统输入和输出关系:
|R,↑〉→-|R,↑〉,|R,↓〉→|R,↓〉,|L,↑〉→|L,↑〉,|L,↓〉→-|L,↓〉
(6)
2 Bell态极化纠缠浓缩方案
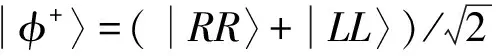
|φ〉=α|RR〉+β|LL〉
(7)
这里叠加项的系数满足|α|2+|β|2=1.
2.1 未知系数非最大纠缠Bell态极化纠缠浓缩方案
假定Alice和Bob不知道噪声对纠缠态的影响情况,即不知道叠加态的系数α与β.如果纠缠源产生的多个纠缠光子对在传送过程中可以看成经历相同的退相干作用,即集体噪声的作用,则通信双方可以获得多个相同的非最大纠缠Bell态.应用图2所示的纠缠浓缩线路即可实现未知系数的非最大纠缠Bell态的极化纠缠浓缩.
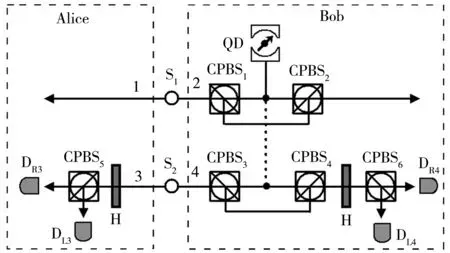
图2 基于单边腔量子点耦合系统非线性实现的未知系数非最大纠缠Bell态纠缠浓缩
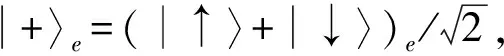
|φ〉12⊗|φ〉34⊗|+〉e
(8)
圆偏振光分束器(CPBS)的作用是透射右圆偏振光子,反射左圆偏振光.如图2,当光子2和光子4通过CPBS1和CPBS3进入单边腔量子点耦合系统,按照公式(6)的规则被反射出来,圆偏振光分束器CPBS2和CPBS4将重新合并光子2和光子4的路径,系统态可以表示为
(9)

(10)
光子3和光子4分别通过圆偏振光的Hadamard门,其作用可以表示为
(11)
则(10)式所表示的系统态将演化成为
(12)

与仅通过线性光学元件实现的纠缠浓缩方案不同,没有得到最大纠缠态并不意味着方案一定失败.Alice和Bob可以将得到的纠缠态重新送入线路,执行下一次纠缠浓缩,即实现基于非线性光学的分级浓缩.
由上面的讨论可知,经过一次纠缠浓缩的成功概率是P1=2|αβ|2,经过两次纠缠浓缩的成功概率是P2=2|αβ|2+(|α|4+|β|4)2|αβ|4,经过三次纠缠浓缩的成功概率是P3=2|αβ|2+(|α|4+|β|4)2|αβ|4+(|α|4+|β|4)(|α|8+|β|8)2|αβ|8,…,即通过分级浓缩可以提高纠缠浓缩的成功概率.
2.2 已知系数非最大纠缠Bell态极化纠缠浓缩方案
如果非最大纠缠Bell态|φ〉12=α|RR〉12+β|LL〉12的系数α与β是已知的,则可以通过辅助光子 |φ〉3=α|R〉3+β|L〉3实现非最大纠缠Bell态的极化纠缠浓缩.仅借助线性光学元件实现的纠缠浓缩的最大成功概率是2|αβ|2,借助单边腔量子点耦合系统的非线性和分级浓缩思想可以提高纠缠浓缩的成功概率,方案如图3所示.

图3 基于单边腔量子点系统非线性实现的已知系数非最大纠缠Bell态纠缠浓缩
系统的初态可表示为
|φ〉12⊗|φ〉3⊗|+〉e
(14)
光子2、光子3与量子点相互作用后,系统态可以表示为
(15)
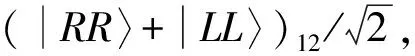
如果Bob对量子点内电子自旋测量结果是|+〉e,即系统态塌缩为非最大纠缠态α2|RRR〉123+β2|LLL〉123.通过对光子3执行与上一结果类似的操作,Alice和Bob可以获得非最大纠缠态α2|RR〉12+β2|LL〉12.Alice和Bob可以令两个光子再次进入极化纠缠浓缩线路,执行分级浓缩从而提高纠缠浓缩的成功概率.
3 总结
借助单边光学微腔量子点耦合系统,我们提出了一个未知系数非最大纠缠Bell态的纠缠浓缩方案和一个已知系数非最大纠缠Bell态的纠缠浓缩方案.与仅应用线性光学元件实现的纠缠浓缩方案相比,本文提出的方案因为应用了光学非线性相互作用,可以通过增加分级纠缠浓缩环节提高方案的成功概率.
以上两个方案也可以推广为多方共享GHZ纠缠网络的纠缠浓缩方案.多光子GHZ非最大纠缠态 |φ〉12…n=α|RR…R〉12…n+β|LL…L〉12…n和Bell类非最大纠缠态|φ〉12=α|RR〉12+β|LL〉12都有两个不相等的复系数α和β,因此可以应用同样的纠缠浓缩方法.此外,Bell类非最大纠缠态和多光子GHZ非最大纠缠态中所有量子比特都是对称的,对纠缠态中任何一个量子比特执行操作都是等价的,因此执行纠缠浓缩的操作者可以由Bob换成参与纠缠共享的其他任意一人.
