一类变系数欧拉函数方程φ(abcd)=mφ(a)φ(b)+nφ(c)φ(d)的可解性
2022-07-25朱萍萍王学花
朱萍萍,孙 钊,王学花
(1.安徽大学江淮学院 公共基础教学部,安徽 合肥230039;2.安徽建筑大学 数理学院,安徽 合肥230030;3.安徽大学江淮学院 理工部,安徽 合肥230039)
0 引言
∀n≥1,欧拉函数φ(n)表示[1,n-1]中与n互质的个数,欧拉函数是数论函数中的基本函数.近年来,对欧拉函数的性质以及欧拉方程的求解方法的研究一直为众多学者所关注[1-8].如文献[2]、[3]、[6]、[8]研究了如何求解三元常系数欧拉方程的正整数解;文献[4]研究了方程φ(abcd)=φ(a)+2φ(b)+3φ(c)+4φ(d)-6的可解性.本文基于上述文献的启发下,研究变系数混合方程φ(abcd)=mφ(a)φ(b)+nφ(c)φ(d)可解性问题,并给出了当m=3,n=4时该方程的全部173组正整数解.
1 相关引理
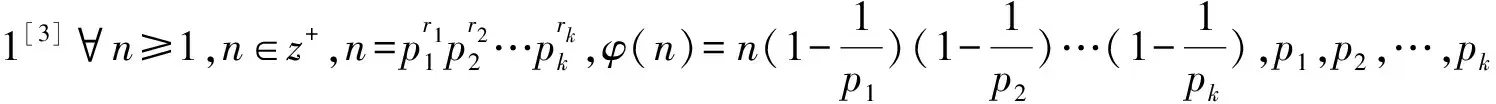
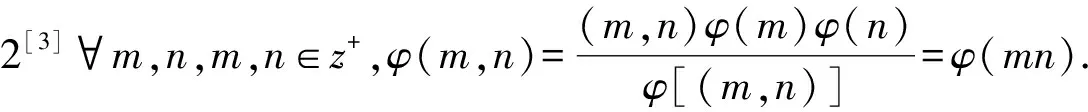
引理3[3]∀n≥2时,φ(n) 定理 欧拉方程φ(abcd)=mφ(a)φ(b)+nφ(c)φ(d)(m=3,n=4)的173组正整数解为: (a,b,c,d)=(3,16,5,1),(3,16,1,5),(16,3,1,5),(16,3,5,1),(1,17,5,1),(1,17,5,2),(1,17,8,1),(1,17,10,1),(1,17,12,1),(1,32,5,1),(1,34,5,1),(1,48,5,1),(1,17,3,1),(1,17,4,1),(1,17,3,2),(2,17,3,1),(1,32,3,1),(1,34,3,1),(1,40,3,1),(17,1,5,1),(17,1,5,12),(17,1,8,1),(17,1,10,1),(17,1,12,1),(32,1,5,1),(34,1,5,1),(48,1,5,1),(17,1,1,5),(17,1,12,5),(17,1,1,8),(17,1,1,10),(17,1,1,12),(32,1,1,5),(34,1,1,5),(48,1,1,5),(3,5,1,7),(3,5,2,7),(3,5,1,14),(3,8,1,7),(3,10,1,7),(4,5,1,9),(6,5,1,7),(3,5,7,1),(3,5,7,2),(3,5,14,1),(3,8,7,1),(3,10,7,1),(4,5,9,1),(6,5,7,1),(5,3,1,7),(5,3,2,7),(5,3,1,14),(8,3,1,7),(10,3,1,7),(5,4,1,9),(5,6,1,7),(5,3,7,1),(5,3,7,2),(5,3,14,1),(8,3,7,1),(10,3,7,1),(5,4,9,1),(5,6,7,1),(1,15,7,1),(1,15,7,2),(1,16,7,1),(1,16,9,1),(2,15,7,1),(1,15,14,1),(1,20,9,1),(1,20,7,1),(1,30,7,1),(1,24,7,1),(15,1,1,7),(15,1,2,7),(16,1,1,7),(16,1,1,7),(16,1,1,9),(15,2,1,7),(15,1,1,14),(20,1,1,9),(20,1,1,7),(30,1,1,7),(24,1,1,7),(15,1,7,1),(15,1,7,2),(16,1,7,1),(16,1,7,1),(16,1,9,1),(15,2,7,1),(15,1,14,1),(20,1,9,1),(20,1,7,1),(30,1,7,1),(24,1,7,1),(1,15,1,7),(1,15,2,7),(1,16,1,7),(1,16,1,7),(1,16,1,9),(2,15,1,7),(1,15,1,14),(1,20,1,9),(1,20,1,7),(1,30,1,7),(1,24,1,7),(3,5,2,4),(4,5,2,3),(4,8,1,3),(4,10,1,3),(6,5,1,4),(6,8,1,3),(5,3,2,4),(5,4,2,3),(8,4,1,3),(10,4,1,3),(5,6,1,4),(8,6,1,3),(3,5,4,2),(4,5,3,2),(4,8,3,1),(4,10,3,1),(6,5,4,1),(6,8,1,3),(6,8,3,1),(5,3,4,2),(5,4,3,2),(8,4,3,1),(10,4,3,1),(5,6,4,1),(8,6,3,1),(1,15,2,4),(1,15,2,6),(1,20,2,3),(1,20,1,4),(1,16,1,4),(1,24,1,4),(2,15,1,4),(1,16,1,6),(2,20,1,3),(2,16,1,3),(1,30,1,4),(1,15,4,2),(1,15,6,2),(1,20,3,2),(1,20,4,1),(1,16,4,1),(1,24,4,1),(2,15,4,1),(1,16,6,1),(2,20,3,1),(2,16,3,1),(1,30,4,1),(15,1,2,4),(15,1,2,6),(20,1,2,3),(20,1,1,4),(16,1,1,4),(24,1,1,4),(15,2,1,4),(16,1,1,6),(20,2,1,3),(16,2,1,3),(30,1,1,4),(15,1,4,2),(15,1,6,2),(20,1,3,2),(20,1,4,1),(16,1,4,1),(24,1,4,1),(15,2,4,1),(16,1,6,1),(20,2,3,1),(16,2,3,1),(30,1,4,1),(3,4,2,2),(4,4,1,2),(4,4,2,1),(8,1,2,2),(8,2,1,2),(8,2,2,1),(12,2,1,2),(12,1,2,2),(12,2,2,1) 证明:对于欧拉方程 φ(abcd)=mφ(a)φ(b)+nφ(c)φ(d) (1) 根据引理2可以得到 则g(abcd)=1,2,3,…,(m+n),若m=3,n=4,则m+n=7,所以,以方程 φ(abcd)=3φ(a)φ(b)+4φ(c)φ(d) (2) 为例,我们来寻求一般变系数欧拉方程的求解方法,其求解过程如下: 根据引理3可知不存在这样的a,b,c,d满足φ(a)φ(b)=5,φ(c)φ(d)=15,接下来就a,b,c,d的取值分别进行讨论. 1.当φ(a)φ(b)=16,φ(c)φ(d)=4时,a,b,c,d的取值须满足如下条件(a,bcd)=1,(b,cd)=1,(c,d)=1,讨论如下: 要使(2)式有解则(a,b,c,d)=(3,16,5,1) 要使(2)式有解,则(a,b,c,d)=(3,16,1,5) 要使(2)式有解,则(a,b,c,d)=(3,16,1,5) 要使(2)式有解,则(a,b,c,d)=(16,3,5,1) 要使(2)式有解,则(a,b,c,d)=(16,3,1,5) 验证可知方程无解. 要使(2)式有解,则(a,b,c,d)=(1,17,5,1),(1,17,5,2),(1,17,8,1),(1,17,10,1),(1,17,12,1),(1,32,5,1),(1,34,5,1),(1,48,5,1) 要使(2)式有解,则(a,b,c,d)=(1,17,1,5),(1,17,2,5),(1,17,1,8),(1,17,1,10),(1,17,1,12),(1,32,1,5),(1,34,1,5),(1,48,1,5) 要使(2)式有解,则(a,b,c,d)=(1,17,3,1),(1,17,4,1),(1,17,3,2),(2,17,3,1),(1,32,3,1),(1,34,3,1),(1,40,3,1) 要使(2)式有解,则(a,b,c,d)=(17,1,5,1),(17,1,5,12),(17,1,8,1),(17,1,10,1),(17,1,12,1),(32,1,5,1),(34,1,5,1),(48,1,5,1) 要使(2)式有解,则(a,b,c,d)=(17,1,1,5),(17,1,12,5),(17,1,1,8),(17,1,1,10),(17,1,1,12),(32,1,1,5),(34,1,1,5),(48,1,1,5) 验证可知方程无解. 验证可知方程无解. 验证可知方程无解. 验证可知方程无解. 2.当φ(a)φ(b)=8,φ(c)φ(d)=6时,结合引理3,就a,b,c,d的取值分如下情形讨论: 要使(2)式有解,则(a,b,c,d)=(3,5,1,7),(3,5,2,7),(3,5,1,14),(3,8,1,7),(3,10,1,7),(4,5,1,9),(6,5,1,7) 要使(2)式有解,则(a,b,c,d)=(3,5,7,1),(3,5,7,2),(3,5,14,1),(3,8,7,1),(3,10,7,1),(4,5,9,1),(6,5,7,1) 要使(2)式有解,则(a,b,c,d)=(5,3,1,7),(5,3,2,7),(5,3,1,14),(8,3,1,7),(10,3,1,7),(5,4,1,9),(5,6,1,7) 要使(2)式有解,则(a,b,c,d)=(5,3,7,1),(5,3,7,2),(5,3,14,1),(8,3,7,1),(10,3,7,1),(5,4,9,1),(5,6,7,1) 要使(2)式有解,则(a,b,c,d)=(1,15,7,1),(1,15,7,2),(1,16,7,1),(1,16,9,1),(2,15,7,1),(1,15,14,1),(1,20,9,1),(1,20,7,1),(1,30,7,1),(1,24,7,1) 要使(2)式有解,则(a,b,c,d)=(15,1,1,7),(15,1,2,7),(16,1,1,7),(16,1,1,7),(16,1,1,9),(15,2,1,7),(15,1,1,14),(20,1,1,9),(20,1,1,7),(30,1,1,7),(24,1,1,7) 要使(2)式有解,则(a,b,c,d)=(15,1,7,1),(15,1,7,2),(16,1,7,1),(16,1,7,1),(16,1,9,1),(15,2,7,1),(15,1,14,1),(20,1,9,1),(20,1,7,1),(30,1,7,1),(24,1,7,1) 要使(2)式有解,则(a,b,c,d)=(1,15,1,7),(1,15,2,7),(1,16,1,7),(1,16,1,7),(1,16,1,9),(2,15,1,7),(1,15,1,14),(1,20,1,9),(1,20,1,7),(1,30,1,7),(1,24,1,7) 所以a,b,c,d的取值满足如下六者之一即可: 要使(2)式有解,则(a,b,c,d)=(3,5,2,4)(4,5,2,3),(4,8,1,3),(4,10,1,3),(6,5,1,4),(6,8,1,3) 要使(2)式有解,则(a,b,c,d)=(5,3,2,4),(5,4,2,3),(8,4,1,3),(10,4,1,3),(5,6,1,4),(8,6,1,3) 要使(2)式有解,则(a,b,c,d)=(3,5,4,2),(4,5,3,2),(4,8,3,1),(4,10,3,1),(6,5,4,1),(6,8,3,1) 要使(2)式有解,则(a,b,c,d)=(5,3,4,2),(5,4,3,2),(8,4,3,1),(10,4,3,1),(5,6,4,1),(8,6,3,1) 要使(2)式有解,则(a,b,c,d)=(1,15,2,4),(1,15,2,6),(1,20,2,3),(1,20,1,4),(1,16,1,4),(1,24,1,4),(2,15,1,4),(1,16,1,6),(2,20,1,3),(2,16,1,3),(1,30,1,4) 要使(2)式有解,则(a,b,c,d)=(1,15,4,2),(1,15,6,2),(1,20,3,2),(1,20,4,1),(1,16,4,1),(1,24,4,1),(2,15,4,1),(1,16,6,1),(2,20,3,1),(2,16,3,1),(1,30,4,1) 要使(2)式有解,则(a,b,c,d)=(15,1,2,4),(15,1,2,6),(20,1,2,3),(20,1,1,4),(16,1,1,4),(24,1,1,4),(15,2,1,4),(16,1,1,6),(20,2,1,3),(16,2,1,3),(30,1,1,4) 要使(2)式有解,则(a,b,c,d)=(15,1,4,2),(15,1,6,2),(20,1,3,2),(20,1,4,1),(16,1,4,1),(24,1,4,1),(15,2,4,1),(16,1,6,1),(20,2,3,1),(16,2,3,1),(30,1,4,1) 验证可得(2)式的解为(a,b,c,d)=(3,4,2,2),(4,4,1,2),(4,4,2,1),(8,1,2,2),(8,2,1,2),(8,2,2,1),(12,2,1,2),(12,1,2,2),(12,2,2,1) 且(a,bcd)=1,(b,cd)=1,(c,d)=1中至少有一个为7,而φ(7)无解. 所以(2)式无解. 本文突破了众多学者对常系数欧拉方程的研究局限性,对任意n元变系数混合型欧拉方程展开研究.文中利用不等式的简单性质对方程进行转化的求解方法,为同类型的方程提供了更简单,更便捷,更容易理解的思路,形如φ(abcd)=mφ(a)+nφ(bcd),φ(abcd)=mφ(a)+nφ(b)+lφ(cd)…等变形形式的n元欧拉方程都可运用本文所提供的解法进行求解,学者也可以在后续的研究中继续探讨其他的求解方法.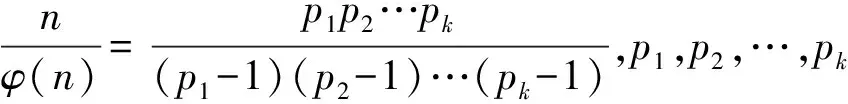
2 定理及其证明
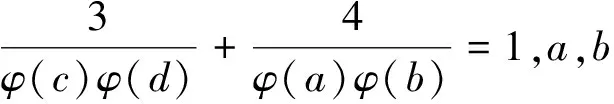
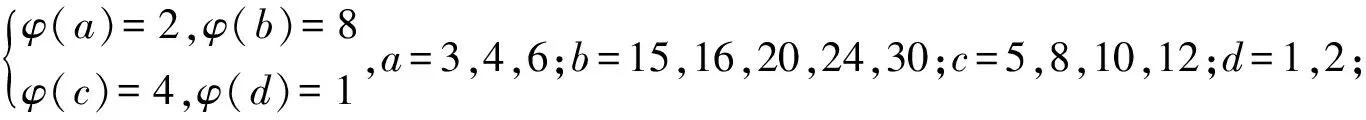
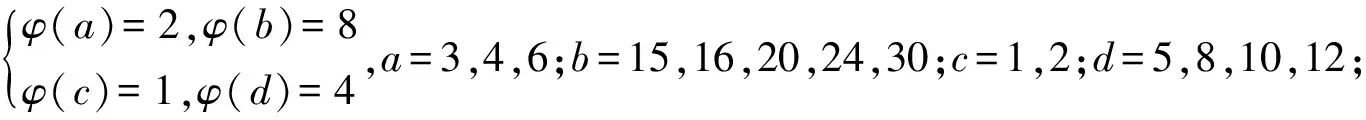

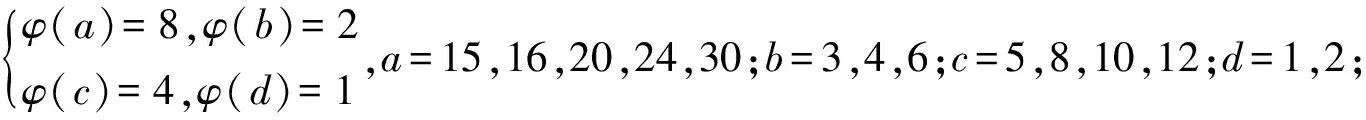
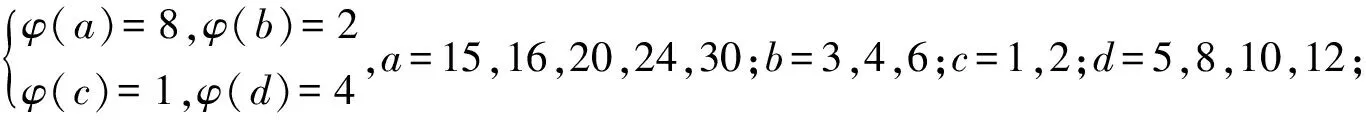
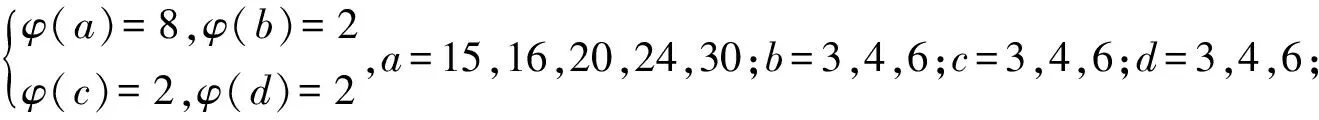

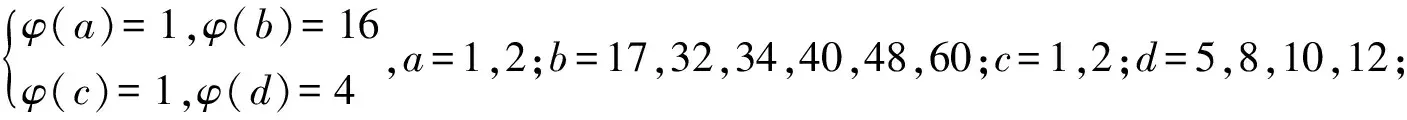
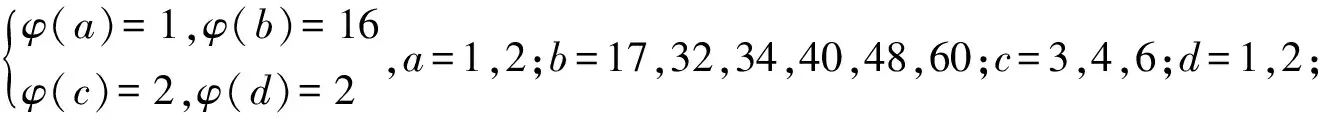
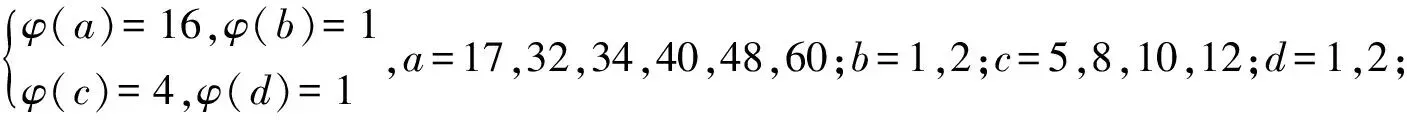
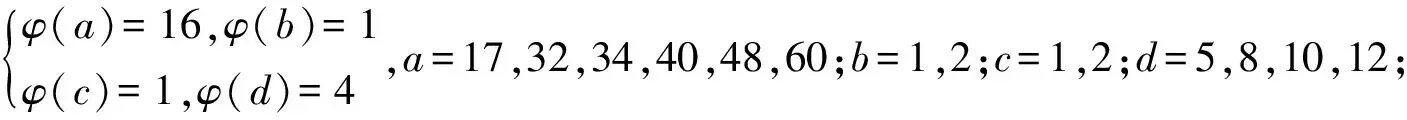
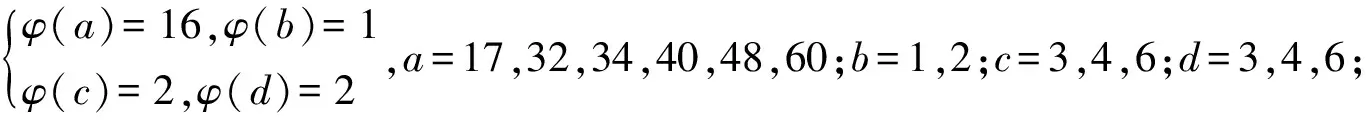
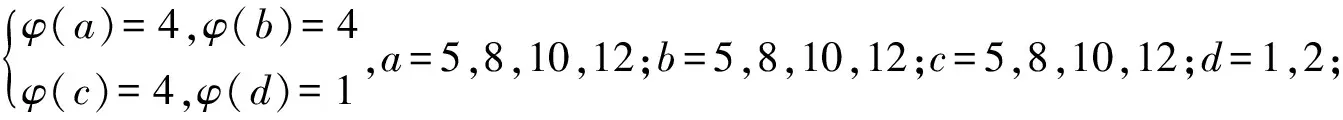
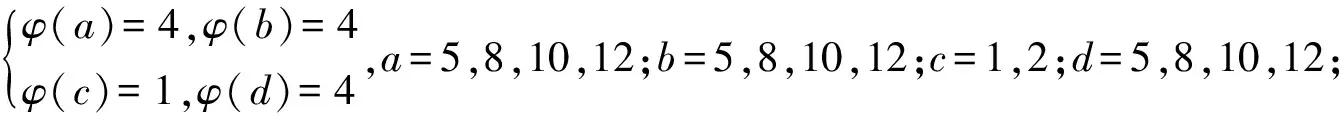
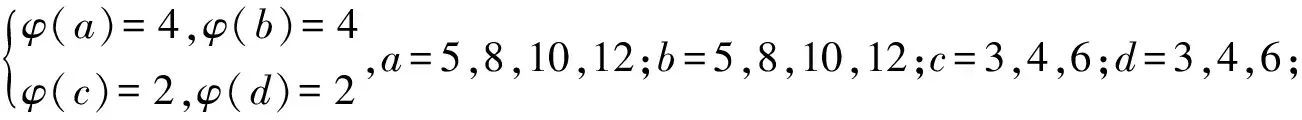
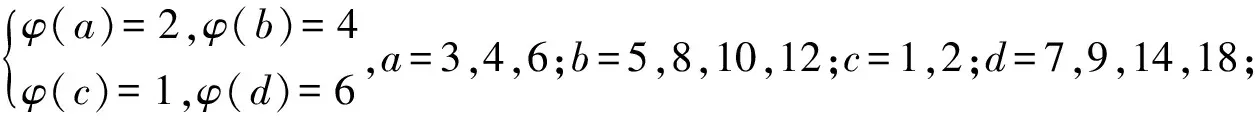
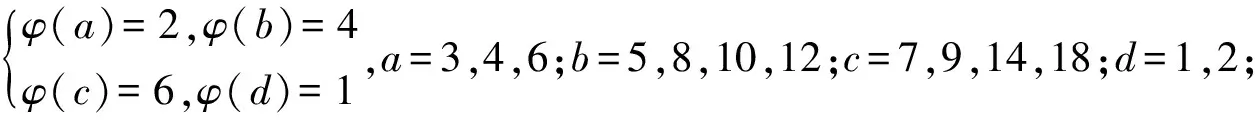

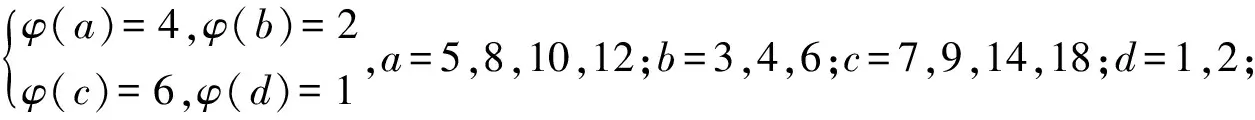
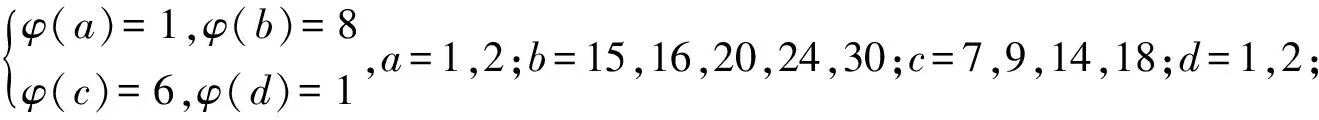
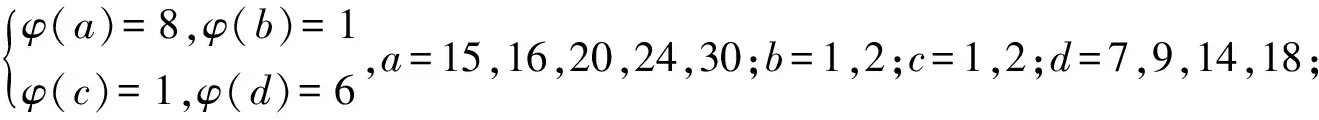
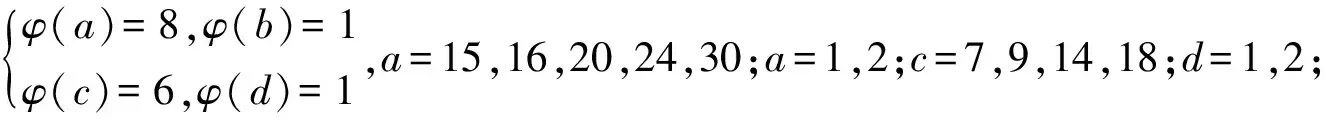


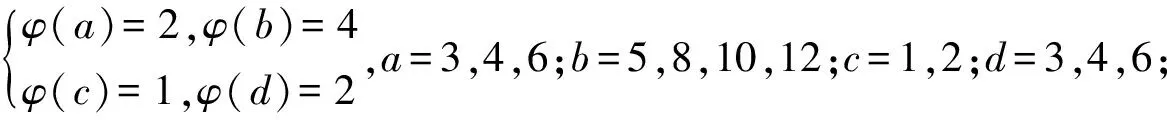
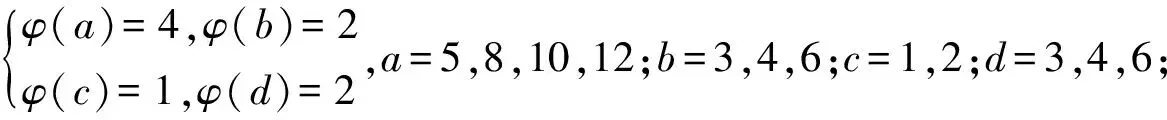
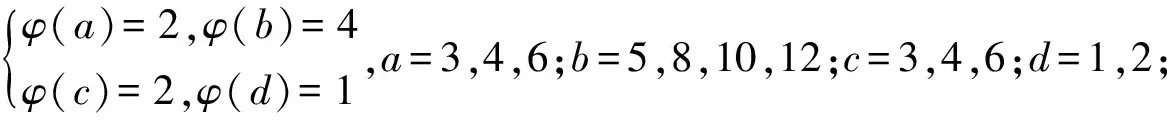
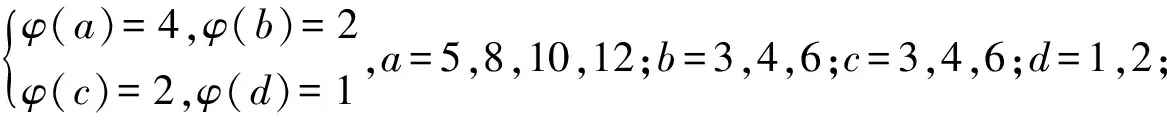


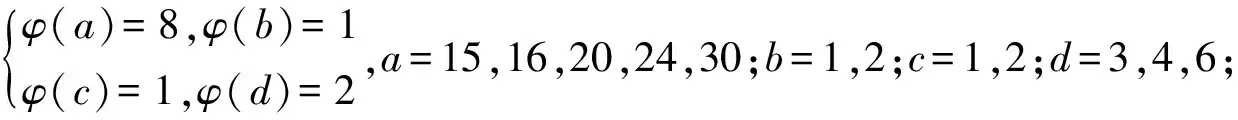
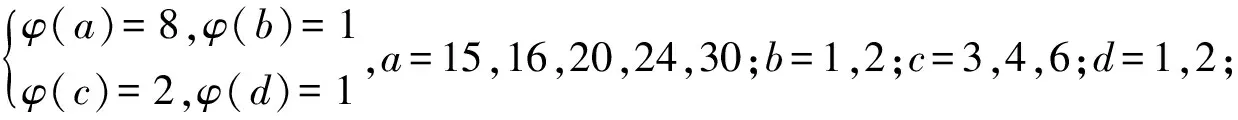
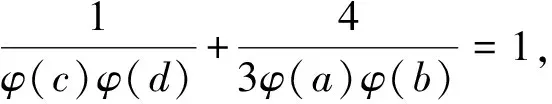
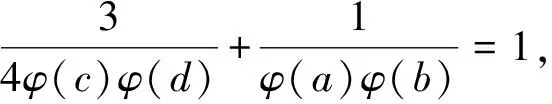
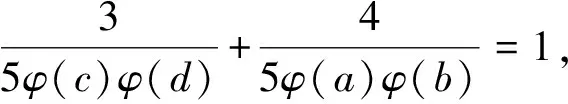
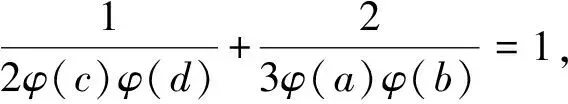
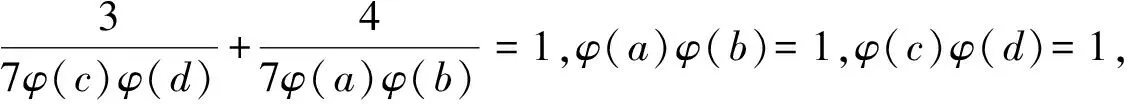
3 研究贡献及研究展望
