具有不同非线性发病率的两菌株模型分析
2022-07-22任亚鑫薛亚奎
任亚鑫,薛亚奎
(中北大学 理学院, 太原 030051)
0 引言
传染病尽管在预防和治疗方面取得了重大进展,但仍在全世界内造成大量死亡。为控制疾病的传播,需要对传染病进行定量研究,从而促进了疾病传播机制的研究。[1-2]
经典流行病模型经常采用双线性发病率和标准发病率。这些模型只能研究相对简单的动力学行为,为模拟更复杂的现象,许多学者引入不同形式的发病率进行建模,比如:饱和发病率、非单调发病率和一般发病率等等[3-5]。例如,Capasso等[3]提出的饱和发病率f(I)S=βSI/(1+αI),其中f(I)在I变大时趋于饱和水平;Xiao等[6]提出了一种非单调函数形式的发病率f(I)S=βSI/(1+αI2),描述了在感染个体相对较多的情况下感染率也会降低的现象。当α=0时,上述2种发病率变为双线性发病率,这可对2种或2种以上菌株进行观察。而在传染病动力学方面的研究工作中,有很多疾病,比如:肺结核、流感、艾滋病等[7-9],是由不同的菌株所引起的。因此,使用多菌株模型可以更好地描述由多个菌株引起的不同疾病的流行[7-14]。
考虑到不同疾病的传播方式不同,人们对其认识和自我防护意识的不同,受Yates[15]的启发,假设菌株非均匀混合,为模拟这一现象,本文建立并分析了具有发病率为βIS/(1+αI)和βIS/(1+αI2)的两菌株的SEIR传染病模型。
1 模型建立
模型包含6个变量,即易感个体S、潜伏个体E1和E2、感染个体I1和I2、恢复个体R。 假设无因病死亡,新生儿均为易感个体,不考虑疾病的垂直传染。可建立如下模型:
(1)

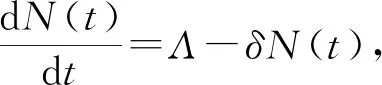
2 基本再生数及平衡点的存在性
由于模型(1)的前5个方程与R无关,所以模型(1)可以简化为:
(2)
根据下一代矩阵算法[16],得到
计算得
从而
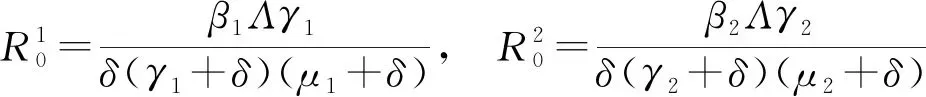
令
a=γ1+δ,b=γ2+δ,c=μ1+δ,d=μ2+δ
则有
定理1模型(2)有4个平衡点:
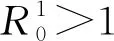
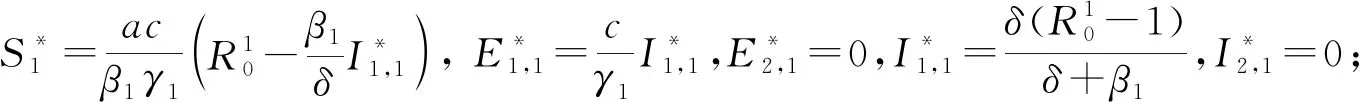
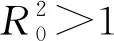
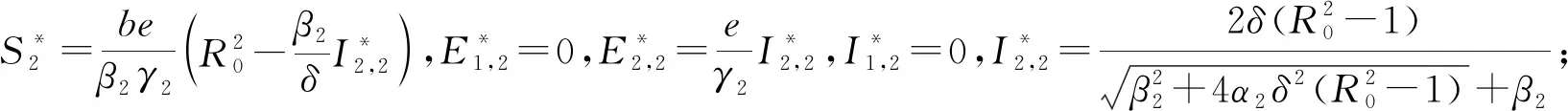
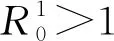

3 平衡点的稳定性

证明构造如下Lyapunov函数
计算L0沿着模型(2)的导数,得
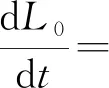
由算术平均值与几何平均值之间的关系,有
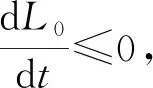

证明构造如下Lyapunov函数
计算L1沿着模型(2)的导数,得
令模型(2)右端等于零,在X1处有
因此
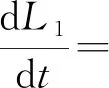
由算术平均值与几何平均值之间的关系,有
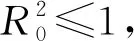


证明构造如下Lyapunov函数
计算L2沿着模型(2)的导数,得

令模型(2)右端等于零,在X2处有
因此

由算术平均值与几何平均值之间的关系,有
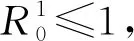
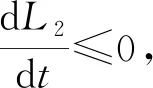
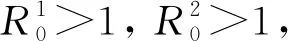
证明构造如下Lyapunov函数
令模型(2)右端等于零,在Xt处有
计算L3沿着模型(2)的导数,得
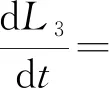
由算术平均值与几何平均值之间的关系,有
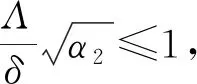

4 数值模拟与讨论
为验证得到的结果,对模型(2)各平衡点的全局稳定性进行数值模拟。模型初始值设置为(S(0),E1(0),E2(0),I1(0),I2(0))=(20,8,8,2,3)。参数选取见表1,其中部分源于文献[18]。
表1 参数值

参数图1图2图3图4Λ0.8000.8000.7500.800δ0.1000.1000.1000.100β10.1000.4500.1100.300β20.1100.0900.8000.200γ10.4000.4000.3300.600
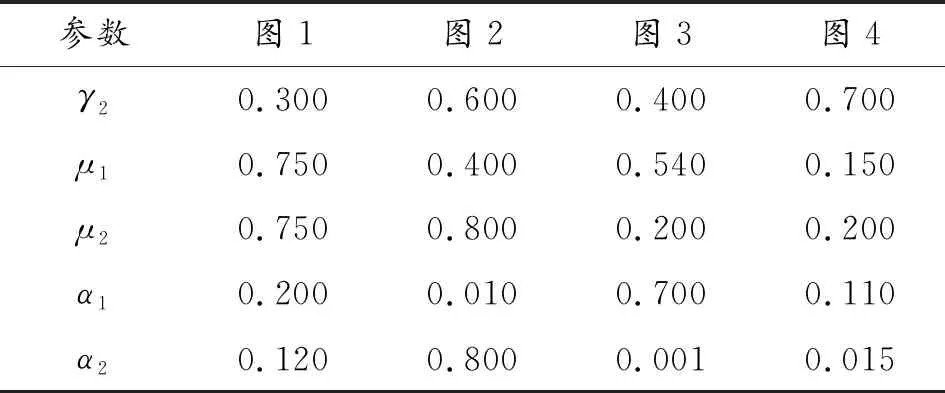
参数图1图2图3图4γ20.3000.6000.4000.700μ10.7500.4000.5400.150μ20.7500.8000.2000.200α10.2000.0100.7000.110α20.1200.8000.0010.015
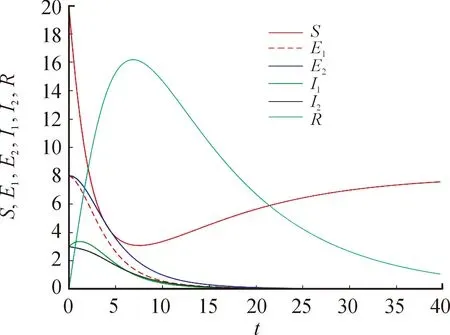
图

图

图

图
图5展示了参数α1和α2对染病者数量的影响。参数选取Λ~μ2与图4中采用数值相同。对2种菌株分别采用相同抑制作用的参数(α1和α2)后,感染个体I2的数量明显低于I1的数量,从而类似菌株2的发病率的疾病相较于类似菌株1更易控制。这表明了解传染病对控制疾病传播有指导作用,积极的控制措施和政策有助于降低感染率。

图5 参数α1和α2对染病者数量的影响
5 结论
采用两菌株模型,研究了具有不同非线性发病率的传染病动力学行为。计算出模型(2)的4个平衡点,借助构造Lyapunov函数,应用LaSalle不变集原理,讨论了各平衡点全局渐近稳定性,并得到其充要条件。数值模拟结果与理论分析相吻合。研究结果表明:
1) 两菌株持续存在时,具有较高基本再生数的菌株将占优势。
2) 研究疾病的发病率对控制疫情蔓延有指导作用,感染个体数量较多的情况下,采取积极的控制措施和政策可有效降低感染个体的数量。
