考虑参数灵敏度的交通仿真模型参数寻优研究

王雪芹，肖志豪

(重庆交通大学 交通运输学院， 重庆 400074)

0 引言

当前，随着计算机技术的飞速发展，交通仿真模型变得越来越复杂。为了更好地理解交通仿真模型，管理模型输出结果的不确定性，有必要对模型参数取值与模型输出结果之间的关系进行深入研究。提高仿真模型输出结果的可控性和有效降低仿真运行成本固然重要，但准确刻画道路交通运行情况才是交通仿真的真正目的。因此，有必要将两者相结合，在提高模型输出结果可控性和降低运行成本的同时对模型关键参数进行标定，使仿真运行结果更加逼近真实的道路交通运行状态，从而为交通控制措施制定和交通改善方案验证等工作提供参考。

国内学者根据我国的实际情况对微观仿真模型的参数标定进行了大量研究。周晨静等[1]以微观仿真模型的参数选取为研究侧重点，进一步完善了微观仿真模型的参数标定过程，以离散度为定量分析指标对各参数离散度的进行量化分析，并根据离散度的大小排序逐步确定关键模型参数。王青燕等[2]总结了微观仿真模型的主要流程，并应用遗传算法对速度参数进行了标定。唐少虎等[3]针对人工萤火虫算法的不足，提出了一种改进自适应步长的人工萤火虫算法，以队列长度为校验指标，并结合VISSIM提供的COM接口技术，设计并实现了基于IAGSO算法的北京信号交叉口仿真参数自动修正流程和方法。张月等[4]通过改进群智能优化算法开发了高效准确的参数修正程序，并将其应用于城市快速路出入口的交通仿真。

国外许多学者已经开始将灵敏度分析引入交通仿真模型参数调整研究。目前，最新的灵敏度分析方法根据数据类型可分为定性和定量两大类。定性方法通常是根据参数对输出结果的贡献来识别影响参数和非影响参数。文献[5]中提出了基于准优化轨迹的基本效应方法，并在文献[6-7]中用于识别交通仿真模型的影响参数和非影响参数，文献[8]也表明这种方法对于高维和计算成本高昂的仿真模型参数灵敏度分析是有效的。另一方面，定量方法能够精确地量化不同模型参数对输出结果的影响，在这类方法中，一种常用的方法是基于方差的灵敏度分析。文献[9]应用定量灵敏度分析方法简化了微观交通仿真模型，在一定程度上降低了模型计算复杂度；文献[10]应用这一方法量化了车辆跟驰模型的参数变化对车辆尾气排放量的影响。除此之外，也有许多定性定量相结合的灵敏度分析方法。例如，文献[11]将OTEE和基于Kriging的灵敏度分析方法相结合，对车辆跟驰模型中的参数进行识别和排序；文献[12]应用了多步全局灵敏度分析对交通仿真模型进行调整，从而对交通安全进行分析。

在上述研究的基础上，将参数灵敏度分析与参数优化取值相结合，应用LH-OAT算法对模型参数进行灵敏度分析；应用GA算法对关键参数进行优化取值；结合实测的交通流数据，分别计算了默认参数和标定参数仿真结果的相对误差。结果表明：对模型参数进行灵敏度分析，从而确定关键参数，可提高模型输出结果的可控性，降低仿真运行的计算成本；对关键参数进行标定时，仿真输出结果更加接近真实的道路交通运行状态，更能精准刻画道路交通运行特征。

1 仿真模型参数标定方案设计

以VISSIM仿真软件中的车辆跟驰模型和车辆换道模型为研究对象，对其包含的参数进行灵敏度分析和优化取值。2个模型的主要参数及其取值范围如表1所示。

表1 2个模型的主要参数及其取值范围

1.1 校验指标选取

为了对比默认参数模型与标定参数模型的仿真效果，选取路段平均行驶速度和路段通行能力作为校验指标。其中，路段通行能力是指单位时间内通过断面的最大车辆数，根据路段交通量调查可直接获得；路段平均行驶速度需要结合路段长度以及车辆通过此路段的行驶时间进行计算，具体表示为：

(1)

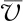
1.2 参数灵敏度分析

1.2.1LH-OAT算法

为了增加对模型输出结果的可控性，从改变模型参数大小对模型输出结果产生影响的角度出发，引入LH-OAT算法对仿真模型参数的灵敏度进行分析研究，从而确定影响模型输出结果的关键参数，达到增强模型可控性、提高模型运行效率的目的。

LH-OAT算法[13]是一种全局灵敏度分析方法，是LHS和OAT的结合，它综合了LHS的稳定性和OAT的精准性，能够有效捕捉影响模型输出结果的关键参数，达到简化模型的目的。

LHS是一种分层随机抽样方法，计算过程具体如下：将n个模型参数分别在其取值范围内等分成m层，且各参数在每层出现的可能性相等；每个参数选取m个随机值，保证每个参数在m层取值空间中的每层仅抽样1次；最后将各参数随机组合，形成m个参数组合方案。作为一种高效的抽样方法，LHS能通过较少迭代次数的抽样准确地重建输入分布，在变量的分布区间进行高效采样。

OAT灵敏度分析方法是一种局部灵敏度分析方法，其基本原理是：假设模型包含了n个参数，根据控制变量法的基本原则，每次只对其中1个参数进行微小扰动，其余参数保持不变；将扰动后的参数组合方案代入模型进行试验，然后将模型输出结果代入目标函数，计算每次扰动后目标函数的变化情况，从而精准刻画参数变化对模型输出结果的影响；共进行n+1模型试验即可得到各参数的局部灵敏度。

LH-OAT通过LHS对各参数进行分层随机抽样，随机组合得到m个抽样参数组合；然后应用OAT分别对这m个参数组合中的各参数进行局部灵敏度分析；最后对各参数的局部灵敏度值取平均，从而实现各参数的全局灵敏度分析。LH-OAT的具体计算步骤：

1) 假设模型有n个参数，将每个参数在其取值范围内等分成m层；

2) 应用LHS在每个分层上抽取1个样本点，生成m个抽样参数组(包含所有参数的集合)；

3) 为每个分层设置1个参数基准值，并进行k次试验，将模型输出结果代入目标函数M。选用纳什效率系数(NSE)作为目标函数，计算式为：

(2)

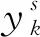
4) 根据局部灵敏度法(OAT)的基本原理，对包含n个参数的抽样参数组进行n次扰动，每次扰动只改变1个参数的大小，计算每次扰动后抽样参数组目标函数的变化情况，根据扰动后抽样参数组和基准参数组的目标函数计算结果，得到各参数的相对灵敏度，计算表达式为：

(3)

式中：TSi,m为第m层参数ei的相对灵敏度，i∈[1,n]；Mm为第m层基准参数组的目标函数值；Mm(e1,…eiαi,…en)为第m层抽样参数组中参数ei扰动后的目标函数值；αi为第m层抽样参数组中参数ei的扰动幅度，i∈[1,n]。

5) 对各参数的相对灵敏度求均值即可得到各参数的全局灵敏度，表达式为：

(4)

式中：GSi为参数ei的全局灵敏度，i∈[1,n]。

为了使仿真模型参数之间的灵敏度具有可比性，将灵敏度划分为4个等级，如表2所示。数值越大，说明该参数的灵敏度越高，对仿真模型输出结果的影响也更大。

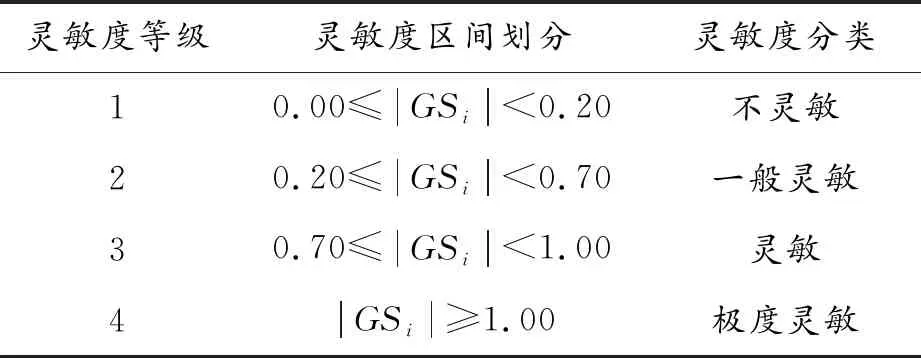
表2 灵敏度分类

1.2.2扰动分析法

LH-OAT算法中的OAT在进行局部灵敏度计算时，需要对各参数分层区间的抽样结果进行一定幅度的扰动。根据扰动分析法[14-15]的基本原理，对参数的扰动幅度进行分析。

扰动分析法的基本原理：假设有n个模型参数，分别对每个模型参数的基准值进行l次不同幅度的扰动，并将扰动后的参数组合方案代入模型进行试验，计算每次参数扰动后，模型输出结果的变化率为：

(5)

式中：βl为参数ei进行幅度为αl的扰动后，模型输出结果的变化率；T(e1,…eiαl,…en)为参数ei进行幅度为αl的扰动后的模型输出结果；T(e1,…ei,…en)为参数ei为基准值时的模型输出结果；αl为参数ei的扰动幅度。

由于每个参数都进行了l次不同幅度的扰动，根据相邻两次参数扰动后模型输出结果的变化率，可以得到一个相对变化率，然后对所有相对变化率取平均值，作为模型输出结果的平均变化率，其计算式见式(6)。根据模型输出结果的平均变化率可反推得到参数的平均扰动幅度。

(6)

式中：S为模型输出结果的平均变化率；βj为参数扰动幅度为αj时，模型输出结果的变化率,j∈[1,l-1]；βj+1为参数扰动幅度为αj+1时，模型输出结果的变化率,j∈[1,l-1]；βa为βj和βj+1的均值。

1.3 参数优化取值

遗传算法[16](GA)是一种基于自然选择和群体遗传机理的搜索算法，它模拟了自然选择和自然遗传过程中的繁殖、杂交和突变现象，具有良好的全局搜索能力。在利用GA寻找最优解时，所有可能出现的解都可以被编码成“染色体”，一定数量的染色体就构成了群体。在GA开始阶段，总是随机产生一定数量的染色体，即编码初始化；然后根据预定的目标函数对每一代的染色体进行适应度评估，再通过选择、交叉、变异，生成一代又一代新的染色体，每一代的染色体由于继承了上一代染色体的优良性状，因而在性能上要优于上一代，逐步朝着最优解的方向进化。

为了模拟道路交通运行，捕捉道路交通运行特征，进而对道路交通流进行管理控制或对交通改善控制措施进行评估分析，越来越多的仿真模型被开发出来。大多数仿真模型由不同的参数按一定的规则构建而成，不同的道路交通运行条件下，仿真参数的取值也会发生变化。因此，根据实际的道路交通运行情况对交通仿真模型的参数进行优化取值，也可以看作是由仿真模型参数组合方案构成的群体逐步进化的过程。应用GA对仿真模型参数进行优化取值的主要流程如图1所示。

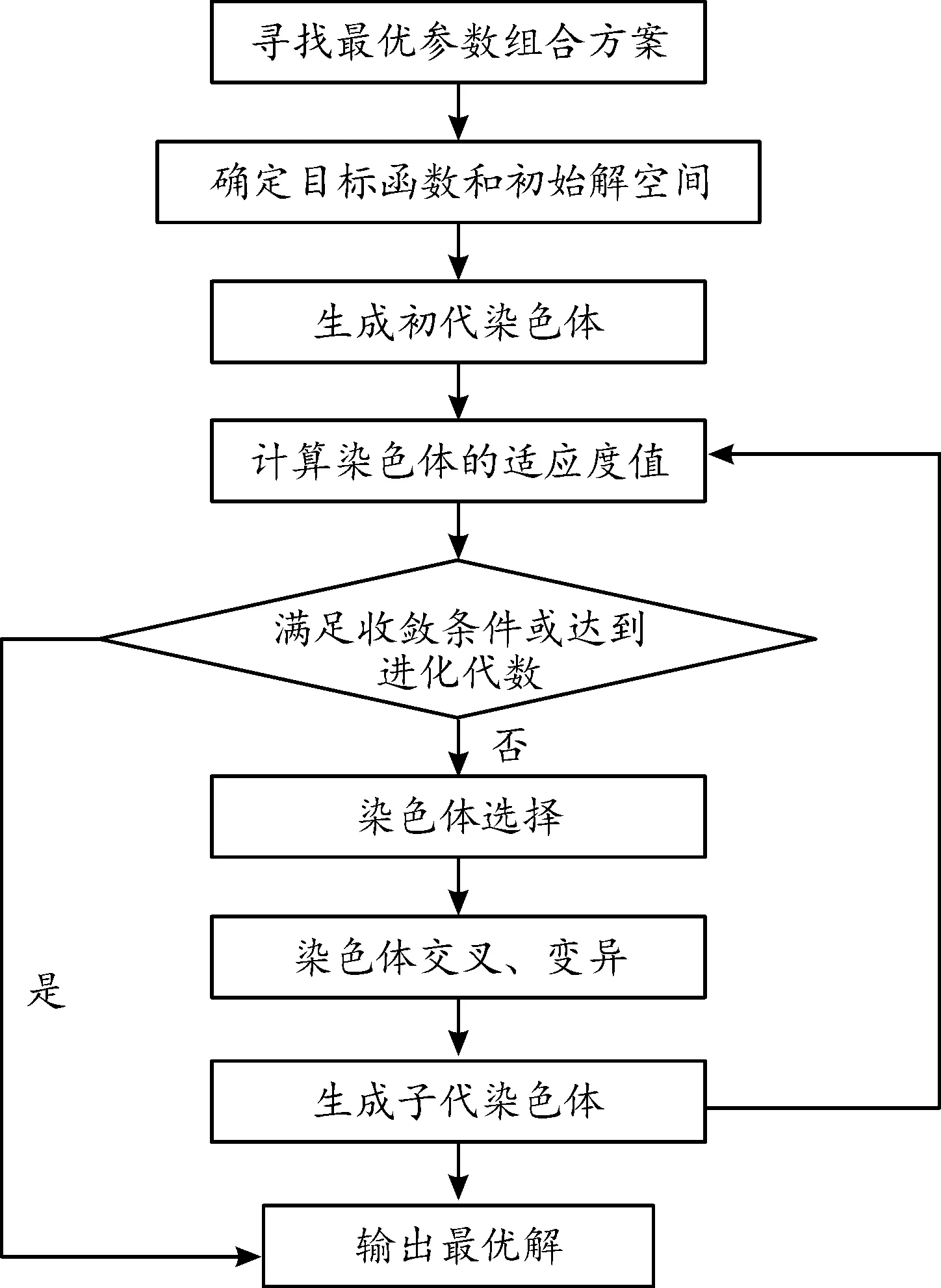
图1 遗传算法流程框图

遗传算法(GA)的计算步骤：

1) 编码初始化。在各参数的取值范围内随机产生i个的参数组合方案(即i条初代染色体)；

2) 计算适应度函数。将模型参数视为基因，参数组合方案视为染色体，对每条染色体进行适应度评价。把模型输出结果的相对误差作为适应度函数，计算式为：

(7)

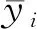
3) 计算选择函数。确定变异或重组的染色体，以及被选择的染色体将产生多少个子代染色体；

4) 变异重组。经过选择操作保存下来的染色体，首先各参数按照一定的幅度进行扰动，生成一定数量的新参数；然后各参数随机组合生成一定数量参数组合方案；

5) 判断迭代终止条件。对新产生参数组合方案进行适应度函数计算，若计算结果逐渐趋于稳定，则停止迭代；否则，继续进行变异重组等操作，直至满足迭代终止条件。

2 仿真模型参数标定试验

根据上述仿真模型参数标定设计方案，选取重庆市内环快速路北环立交进—出型交织区为调研对象，如图2所示。通过无人机拍摄和人工计数相结合的方法进行交通数据采集。

图2 交织区示意图

2.1 数据采集

在交织区路段内设置间距为80 m的2个固定点位。为了简化模型计算，将2个固定点位的间距视为交织区长度，并测算2个固定点位之间的车辆平均行驶时间和路段车流量。7∶30—8∶30是早高峰调查时段，17∶30—18∶30是晚高峰调查时段，采集流量数据时以15 min为时间间隔，调查数据经过统一处理和测算，结果分别如图3、表3和表4所示。

图3 交织区构造图

表3 交织区几何数据

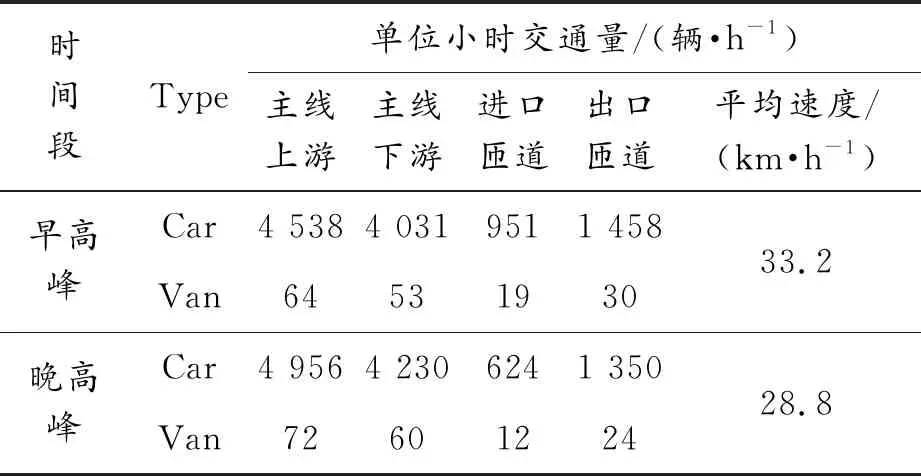
表4 交织区流量数据

2.2 仿真模型搭建

利用实地调查的交织区段道路几何数据以及早晚高峰车流量数据，建立VISSIM交通仿真模型。在建立模型时，主线上游输入流量和进口匝道输入流量分别设置路径决策，同时在主线与匝道合流区域设置优先通行规则。当车辆即将行驶到分、合流区域时，车辆往往会受到车流交织的影响进行减速，因此需设置减速区域；由于主线与匝道输入车辆的期望速度不同，因此分别在进出口匝道处设置期望速度决策点，建立的VISSIM交通仿真模型如图4所示。

图4 VISSIM交通仿真模型

2.3 期望速度分布调整

除仿真模型参数外，交织路段期望速度分布也是影响仿真结果的关键因素。结合爬取到的人和立交至北环立交路段速度数据以及实测交织区段速度数据，采用频数分析法对交织区段早晚高峰的速度数据进行统计分析，以此校验车辆的期望速度分布区间。

以10 km/h为间隔统计出每个速度区间的分布比例，并绘制期望速度区间频数分布图，如图5所示。速度区间35～45 km/h区间比例为10%，45～55 km/h区间比例为13%，55～65 km/h区间比例为26%，65～75 km/h区间比例为39%，75～85 km/h区间比例为12%。最后，将期望速度区间分布作为校验后的主线上游输入车流的期望速度分布。

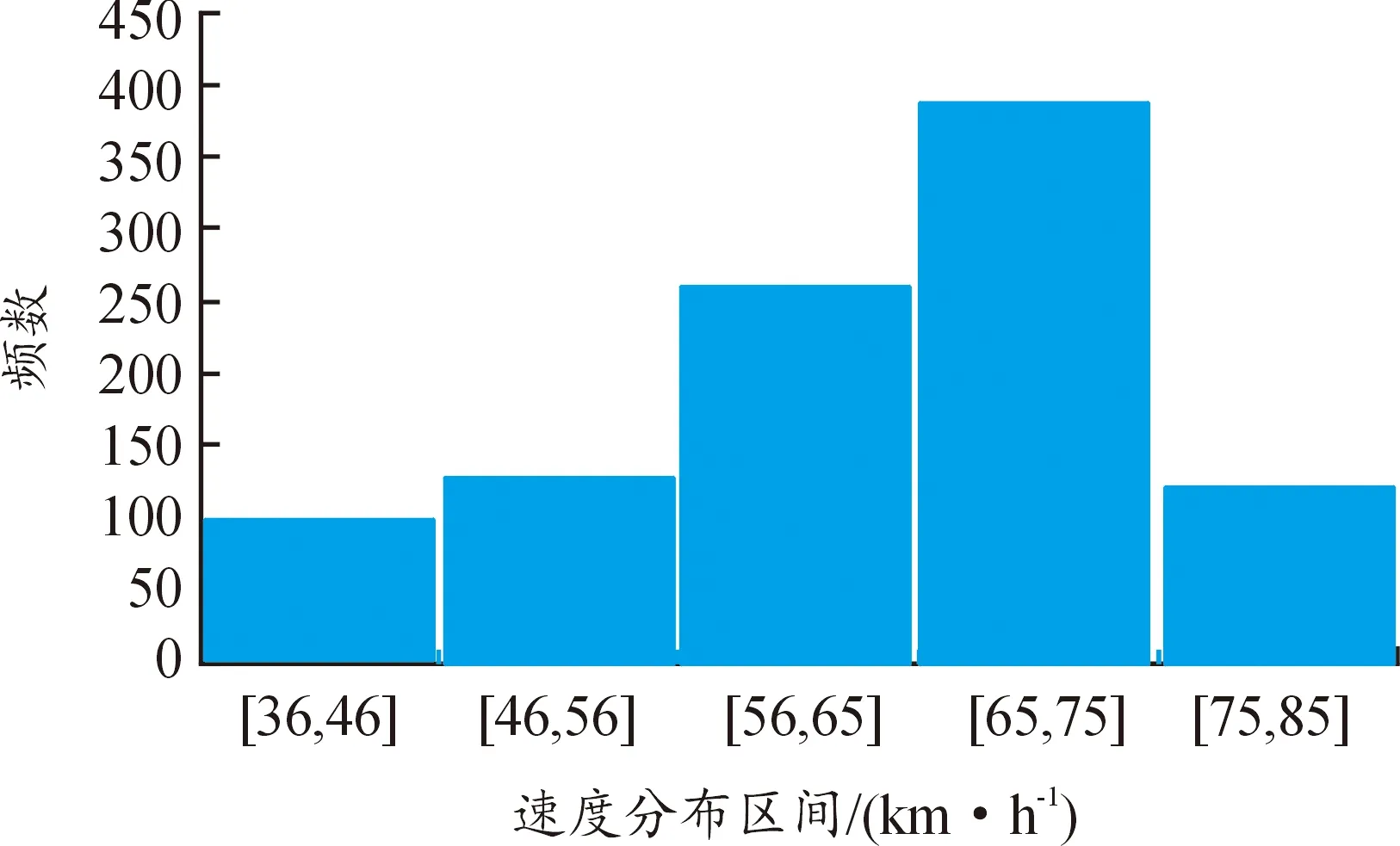
图5 区间车速分布直方图

2.4 仿真参数灵敏度分析

应用LH-OAT算法对车辆跟驰模型和车辆换道模型的13个参数进行灵敏度分析。

1) 将各参数在其取值范围内等分成4个空间层，每层设置1个参数基准值，生成4个基准参数组，分别进行仿真模拟试验，并将仿真输出结果带入目标函数进行计算。

2) 对每层的13个参数随机抽样1次，生成4个抽样参数组；根据参数扰动分析原理，设置10%的扰动幅度，从而对抽样参数集合进行局部灵敏度计算。

3) 对各参数的局部灵敏度求均值，得到各参数的全局灵敏度，计算结果如表5所示。

表5 仿真模型参数灵敏度值

根据参数灵敏度计算结果，可以发现OBd、Npr、AXaverage、ACCmax、ACCac、D、Tdis、GAPmin、ABX、COac，这10个参数对仿真输出结果精确度起关键影响作用，因此将其作为关键影响参数。这在一定程度上简化了仿真模型，提高了模型输出结果的可控性，降低了模型运行的计算成本。

2.5 仿真参数优化取值

2.5.1GA计算步骤

借助Python语言，设计自动仿真运行程序求解各模型参数的标定值。具体实现过程如下：

步骤1编码初始化。将选定的10个待标定参数分别在其取值范围内随机生成70个参数组合方案(70条染色体)；

步骤2染色体适应度评价。首先对这70个参数组合方案(染色体)分别开展5次随机种子实验(20，60，100，140，180)，计算每条染色体仿真输出结果的相对误差及其每一代染色体的相对误差总和，判断相对误差总和是否趋于稳定，若满足条件，则停止迭代，否则进入下一步；

步骤3染色体变异重组。根据每条染色体相对误差的大小进行排序，选取相对误差最小的前20条染色体作为父代染色体进行变异重组。变异原则：在父代染色体的基础上，对各参数进行5%的浮动，生成35条子代染色体；重组原则：在父代染色体的基础上，利用各参数随机组合生成35条子代染色体；

步骤4重复步骤2和步骤3，直至迭代结果满足终止条件，退出实验。

随着迭代优化的逐步推进，参数组合方案的相对误差总和逐渐趋于稳定，共迭代4次，进行 1 400次仿真实验时达到了终止条件。

2.5.2仿真参数标定结果

选取经GA优化处理最终生成的70条子代染色体作为分析对象，对输出的平均行驶速度和通行能力取均值，作为此参数组合方案的最终仿真结果，如图6所示。

图6 校验指标仿真结果

将仿真结果与实测值进行误差分析，选出相对误差最小且在10%以内的参数组合方案，认为该种方案与真实道路交通运行状态最为接近。各参数组合方案的相对误差计算结果如图7所示。

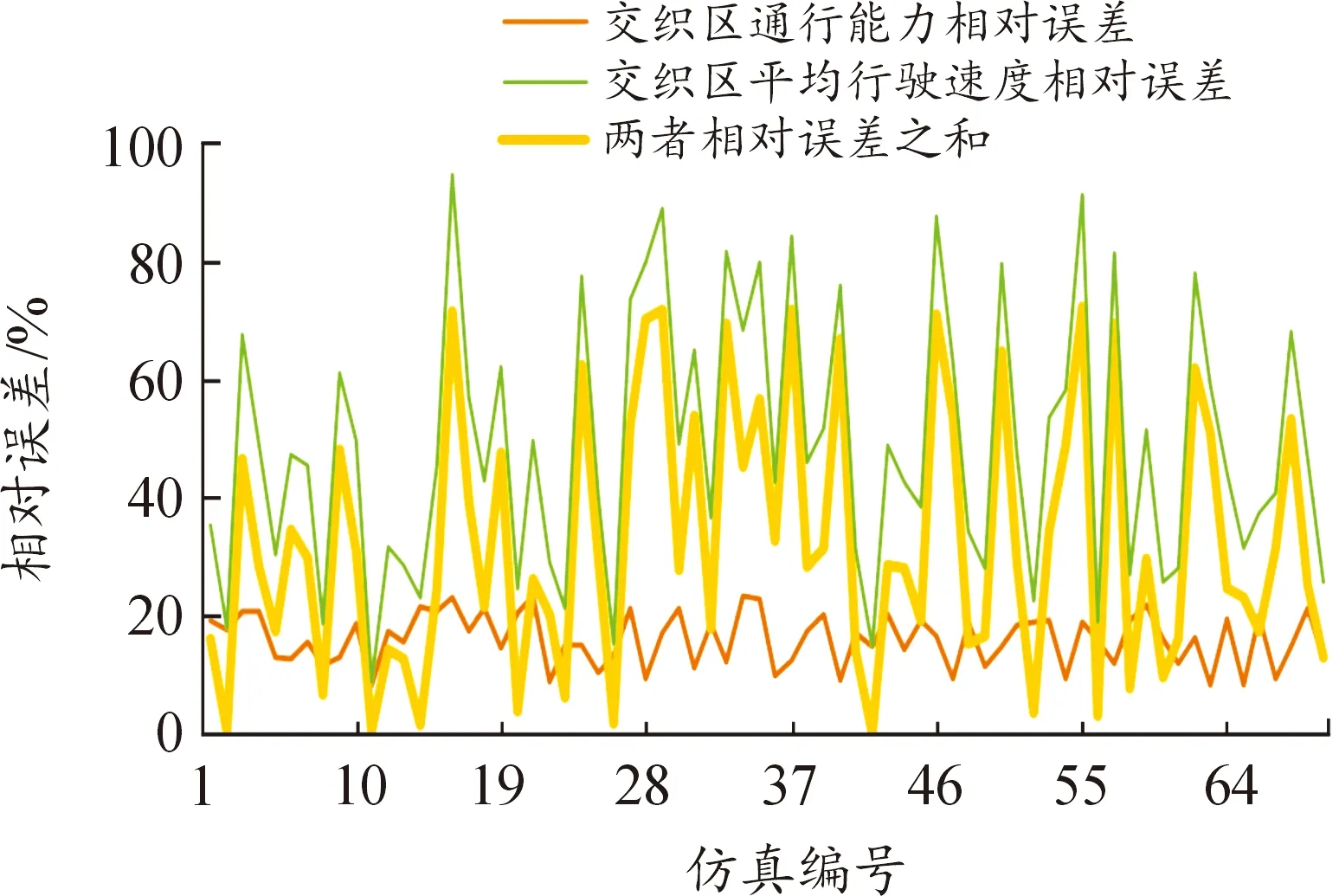
图7 仿真结果与实测值相对误差

通过相对误差分析可知，第11个参数组合方案的平均行驶速度和路段通行能力的相对误差皆最小，且相对误差均在10%以内，对应的仿真输出结果和误差分析结果如表6所示。因此，本次仿真参数标定试验将第11参数组合方案作为最终标定结果，相关参数值如表7所示。

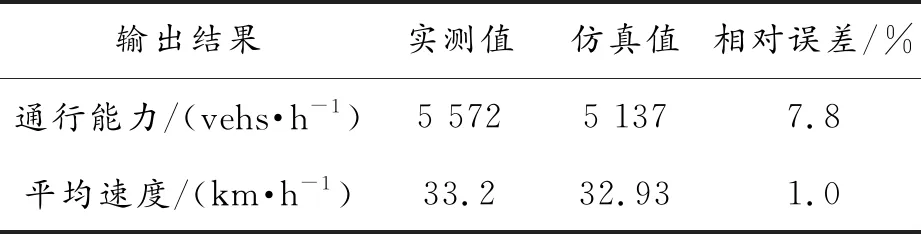
表6 校验指标值误差分析

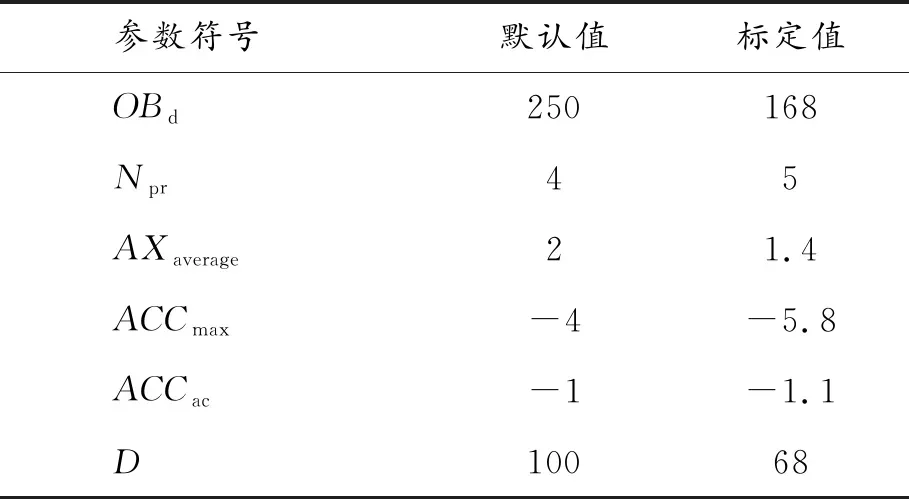
表7 参数标定结果

续表(表7)

2.5.3标定参数验证分析

上文根据交织区早高峰时段的交通运行数据，搭建了交通仿真模型，并对车辆跟驰模型和车辆换道模型的关键参数进行了标定。根据早高峰交通流实测数据，参数标定结果能够很好地反应交织区早高峰时段的交通运行特征。

为了进一步验证标定参数的合理性，将该交织区晚高峰时段的交通流数据带入VISSIM仿真模型，进行5次随机种子试验，并对这5次仿真试验结果取均值，得到交织区晚高峰时段仿真输出结果的最终值，如表8所示。

表8 交织区晚高峰交通流仿真运行结果

根据交织路段晚高峰交通仿真结果可知，路段平均行驶速度和路段通行能力的仿真输出结果分别为26.7 km/h和5 483 vehs/h。结合交织区晚高峰时段的实测交通流数据进行误差分析，校验指标值见表9。

表9 校验指标值

由表9可知，参数标定后的交通仿真模型在对交织区晚高峰时段的交通流进行仿真模拟时，校验指标的输出结果与实测数据的相对误差都在10%以内，能够较好地反映交织区晚高峰时段交通运行的真实情况，进一步说明模型参数得到了合理校正。

3 结论

1) 应用LH-OAT方法进行仿真模型参数的灵敏度分析。综合了拉丁超立方抽样法(LH)的稳定性和局部灵敏度法(OAT)的精确性，并将纳什效率系数(NSE)作为目标函数，对仿真模型参数的灵敏度进行了详尽分析，从而确定了影响仿真模型精度的关键参数，提高了仿真模型输出结果的可控性，降低了仿真模型的运行成本。

2) 在参数灵敏度分析的基础上，应用遗传算法(GA)对关键参数的取值进行了优化校正。对仿真模型的关键参数进行优化取值，使仿真效果更加逼近真实的道路交通运行状态，从而进行道路交通运行状态评估，帮助制定交通控制改善措施和进行交通改善设计方案的评估等。

3) 无论是参数灵敏度还是关键参数优化取值上都直接选用特定算法进行分析，算法的适用性缺乏充分说明。后续将分别对参数灵敏度分析和优化取值这两部分进行多算法对比研究，从而选择精度更高的算法进行模型参数校正。

4) 在进行仿真模型参数标定时，使用的是正常工作日交织区早高峰的交通流数据；进行标定参数的合理性验证分析时，使用的是正常工作日交织区晚高峰的交通流数据。对于城市快速路交织区而言，早晚高峰时段的车流量运行具有极大的相似性，为了进一步分析标定参数的合理性，后续应考虑正常工作日、固定节假日、极端天气等多种条件的限制。