具有换道功能的自适应巡航控制策略研究

胡远志，张 隆，刘 西，雷发林

(重庆理工大学 汽车零部件先进制造技术教育部重点实验室， 重庆 400054)

0 引言

自适应巡航控制(adaptive cruise control,ACC)是智能车的基本功能[1]，能够接管驾驶过程中的部分驾驶任务，在缓解驾驶员驾驶强度的同时，可以有效地提高汽车安全性，以减少交通事故的发生[2]。

传统的ACC系统仅能实现车辆的纵向运动控制，功能相对独立，在面对前方低速行驶的目标车辆时只能低速跟车行驶或请求驾驶员接管等，存在很大的局限性。未来ACC系统必将与其他ADAS系统集成及协同控制以提高ACC系统的实用性[3]。但诸多学者对于ACC系统的研究集中在关键目标识别[4-5]、多模式控制策略[6-8]、控制算法优化[9-11]等方面，仅涉及到ACC系统的纵向运动控制。

目前，对具有换道功能的ACC系统控制策略方面研究较少。党睿娜[12]提出了一种综合周边多车辆信息的换道预警方法，实现了换道工况下周边环境风险判断及预警，其横向控制仍需驾驶员操控；陈碧云[13]提出了具有换道辅助的多模式自适应巡航控制策略，重点研究了换道意图识别方法和换道可行性判断方法，未涉及到横向控制方面的内容；姚军[14]研究了具有转向控制的自适应巡航控制系统，主要研究纵向、横向、横纵向耦合控制，但未涉及换道方面的内容；黄晶等[15]研究了基于前车换道意图辨识的智能巡航控制算法，涉及到ACC车辆的换道功能，对本文的研究具有较大的参考价值，但其仿真工况较为单一，并未涉及到巡航-换道等复合工况。孙小文等[16]将ACC行驶模式划分为巡航、跟车、接管、换道工况，但未对换道工况下的控制策略进行说明。

基于此，本文针对城市快速干道及高速公路工况，对具有换道功能的自适应巡航控制策略展开研究。首先，基于速度不满意累计度设计了多模式切换策略，然后，基于模型预测控制算法设计了定速巡航和跟车巡航纵向控制器、换道轨迹跟踪控制器，并利用五次多项式规划了换道轨迹等。最后，使用Prescan/Carsim/Matlab软件搭建了仿真与测试平台，设计了多种测试工况对本文提出的控制策略进行仿真测试与验证。

1 车辆ACC系统控制策略设计

车辆ACC控制器多采用分层式[17](上下两层)设计方法，本文在沿用前人分层设计方案的基础之上将ACC系统工作模式划分为定速巡航、跟车巡航、换道巡航3种，系统如图1所示。

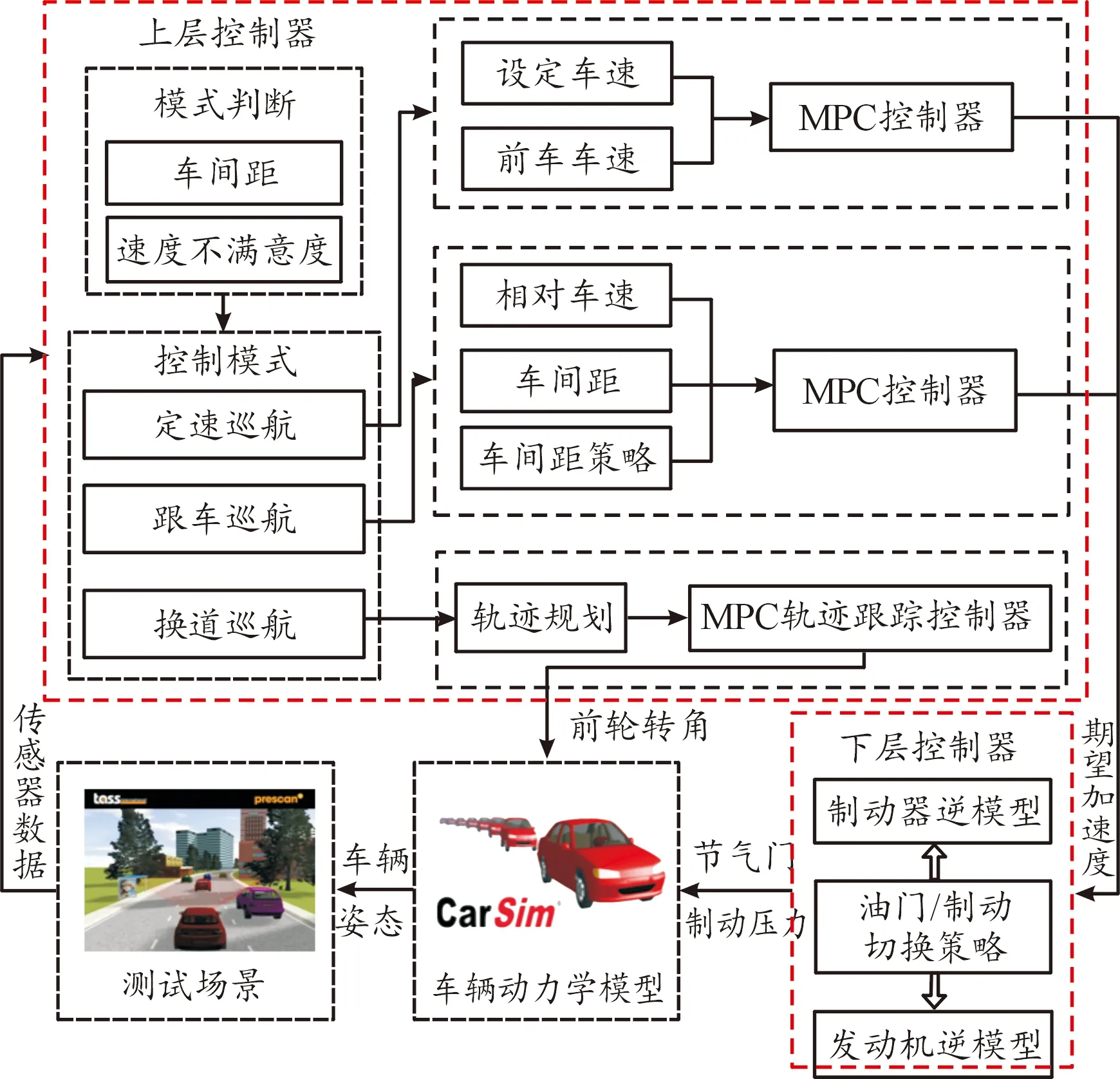
图1 自适应巡航控制系统框图

上层为决策规划层，根据主车前方是否存在有效目标车辆执行定速巡航模式和跟车巡航模式，当主车前方存在有效目标车辆且速度不满意度及邻车道车速优势满足一定条件后将执行换道巡航模式；下层为控制执行层，将上层决策规划的车辆期望纵向加速度根据车辆逆动力学模型转化为油门和刹车控制指令，从而控制车辆的横纵向运动，以实现车辆的巡航功能。

1.1 下层控制器的设计

下层控制器通过控制车辆油门开度和制动轮缸压力实现对上层决策期望加速度的跟踪。根据汽车理论及车辆纵向运动控制逻辑，分别建立了车辆驱动逆模型和制动逆模型，求解油门开度和制动压力，以实现对车辆纵向运动的精确控制。

1.1.1车辆驱动逆模型

汽车理论中，汽车驱动行驶方程的定义如下：

Ft=Ff+Fw+Fj+Fi

(1)

(2)

(3)

(4)

式中:Ff、Fw、Fj、Fi为车辆行驶阻力，Ft为车辆克服行驶阻力所需的驱动力。根据力学相关理论将式(1)展开可得式(2)。式(3)中，δ为旋转质量换算系数。本文的研究仅考虑平直道路工况，即sinα=0、cosα=1，则车辆在行驶过程中的期望发动扭矩可转化为式(4)。

车辆发动机的MAP图关系可表示如下：

Tdes=f(α,ω)

(5)

式中:Tdes为期望的发动机扭矩，α为节气门开度，ω为发动机转速。为了求解期望的节气门开度可将发动机MAP图关系转化如下：

αdes=f(T,ω)

(6)

根据Carsim软件中发动机MAP图中发动机转速、扭矩、节气门开度三者关系，将其转换为逆MAP图，如图2所示。利用查表法可得到发动机期望的节气门开度。

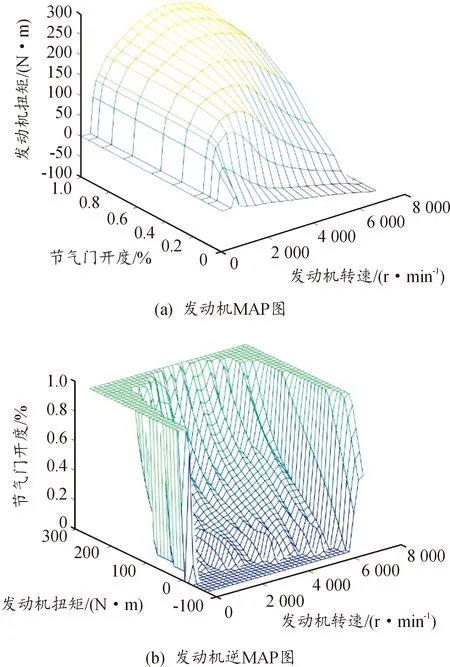
图2 发动机MAP图和逆MAP图

1.1.2车辆制动逆模型

同样，根据式(1)—(3)可推导出车辆制动时期望的制动力：

(7)

则轮缸压力与制动压力的关系可表示如下：

Fdes=k·pdes

(8)

式中:Fdes为期望的制动力，pdes为期望的轮缸压力，k表示制动压力和轮缸压力的比例。则期望的轮缸压力可表示为：

(9)

1.1.3油门/刹车切换逻辑

正常驾车过程中，制动和油门踏板不会同时被操控。为了使控制策略更加符合驾驶员驾驶特性，需制定油门和刹车切换逻辑，以避免油门和制动控制频繁切换。为了得到制动和油门切换的临界值，设定车辆初始速度为120 km/h,带挡滑行直至车辆稳定为怠速状态。根据经验值设定阈值为0.05，则可得车辆油门/刹车切换阈值，如图3所示。

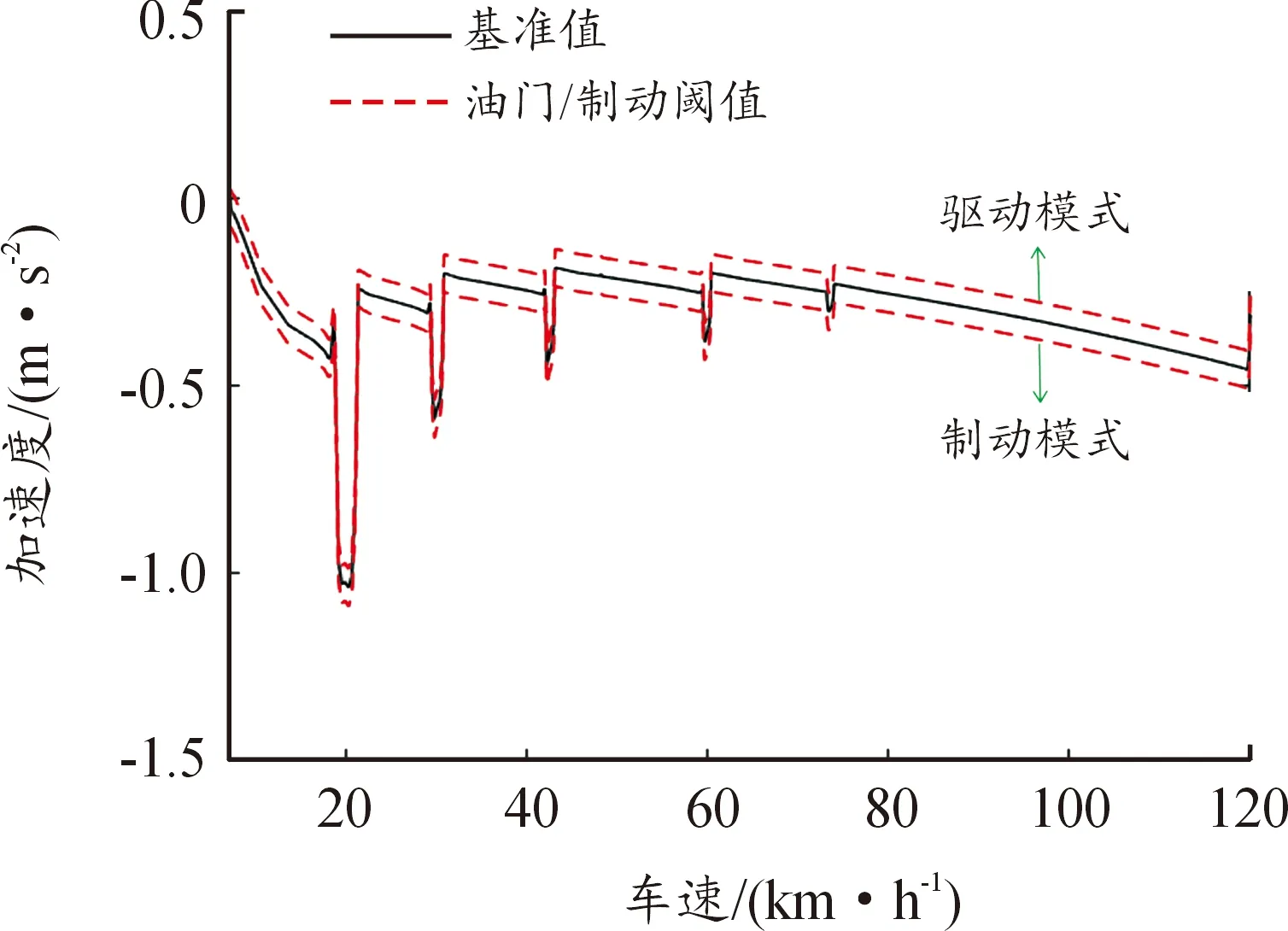
图3 车辆油门/刹车切换阈值

1.1.4下层控制器仿真测试

为了验证下层控制器的准确性及稳定性，设定车辆的初始速度为40 km/h，分别以正弦、斜坡、脉冲信号源作为激励对下层控制器进行仿真测试与参数调整，仿真与测试结果如图4所示。

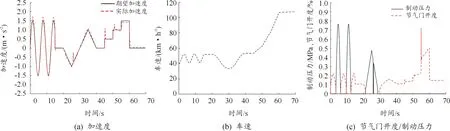
图4 下层控制器仿真测试结果

根据图4中的仿真结果可知，下层控制器可稳定跟踪设定的期望加速度，且油门与制动未出现同时被操控及频繁切换的情况，其中加速度的突变是由于车辆换挡所致。因此，可知本文设计的下层控制器可满足要求。

1.2 上层控制器的设计

1.2.1多控制模式切换策略

本文将ACC车辆的控制模式分为定速巡航、跟车巡航、换道巡航3种，其切换控制逻辑如图5所示。

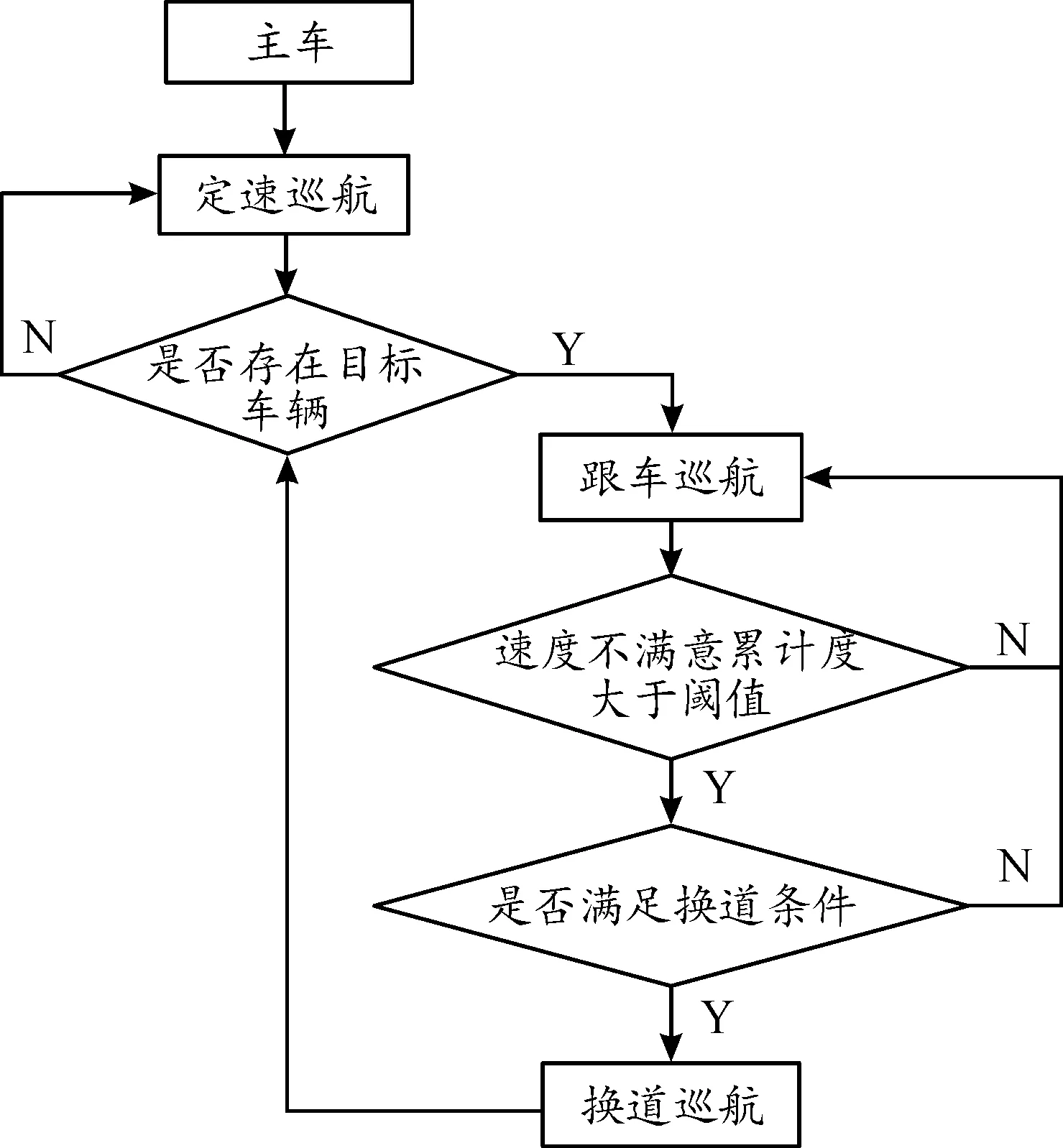
图5 多控制模式切换逻辑框图

根据主车前方是否存在有效目标车辆执行定速巡航和跟车巡航模式，跟车巡航时实时计算驾驶员速度不满意累计度，并对ACC车辆的换道行为进行决策，若满足条件则执行换道巡航模式。

换道行为决策的主要作用是根据当前车辆的状态和环境信息决策是否要触发换道请求，其中涉及到换道安全性、换道后的速度优势、换道触发等。由于文章篇幅有限，本文假定邻车道不存在其他目标车辆，即邻车道具有速度优势且换道安全。另外，ACC车辆跟车时会主动控制车辆安全跟车，本文假定目标车与主车在短时间内纵向运动行为不发生变化，即ACC车辆在换道时不会与目标车发生碰撞，所以只需要对ACC车辆的换道触发机制进行设计。ACC车辆换道的主要原因是目标车辆的速度过低，因此本文以速度不满意累计度模型设计ACC车辆换道的触发机制。

速度不满意累计度模型[18]描述的是期望车速与实际车速的差值随着时间的累积量，令vdes、v分别为期望的车速和实际的车速，则速度不满意度累计度模型可表示如下：

(10)

式中:V(k)为k时刻的速度不满意累计度值，ΔT为采样时间。当V(k)大于设定的阈值时，ACC车辆将被触发进行换道操作。

本文中是否存在目标车辆的判定条件是主车当前车道150 m内是否存在前车，设定速度不满意累计度的阈值为5。

1.2.2车间距策略

车间距策略的最主要作用是根据主车状态和目标车状态求解出主车的期望车间距离，车间距策略主要分为固定车间距策略和可变车间据策略，由于可变车间距策略具有诸多优点而被广泛采用。可变车间距策略根据车头时距的不同又分为可变车头时距策略和固定车头时距策略，由于固定车头时距策略未考虑因素较少，其控制效果较差。因此，本文采用考虑前车车速、加速度的可变车头时距策略。

车间距策略可表示如下：

Δxdes=thv+d0

(11)

th=t0-a(vl-ν)-bal

(12)

式中: Δxdes为期望车间距离，th为车头时距，t0为默认的车头时距，v为主车车速，vl为目标车车速，al为目标车加速度，d0为最小车间距离，a、b分别为系数。

1.2.3纵向期望加速度决策模型

MPC算法由于可约束多目标并在线优化求解，控制效果较好、鲁棒性较强。因此，本文将基于模型预测理论设计车辆的纵向期望加速度决策模型，以求解车辆的期望加速度。

1) 车辆纵向运动学模型

车辆纵向运动学关系示意图如图6，则主车和目标车的纵向运动学关系可表示为：

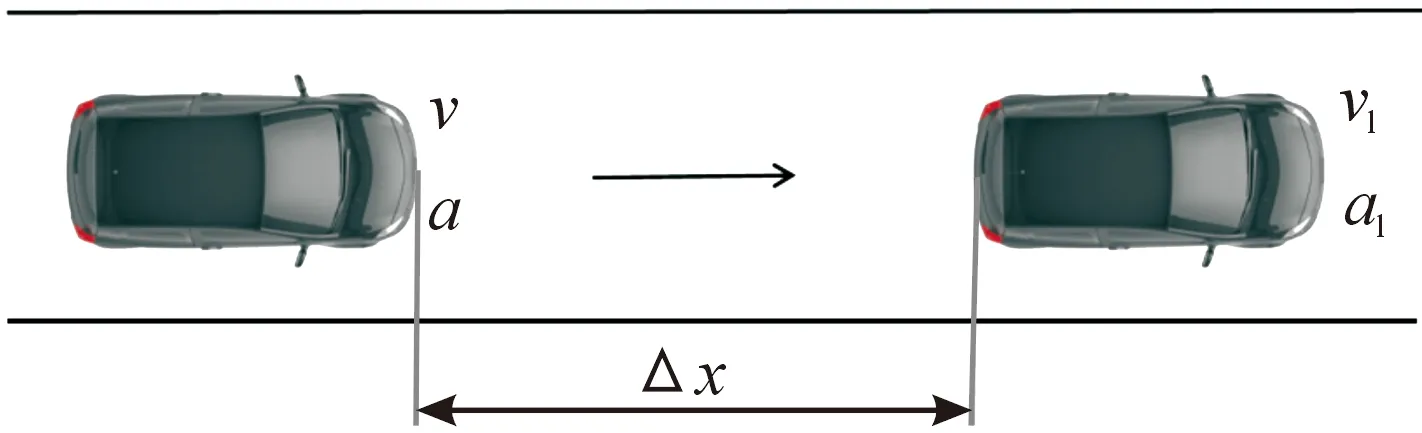
图6 车辆纵向运动学关系示意图

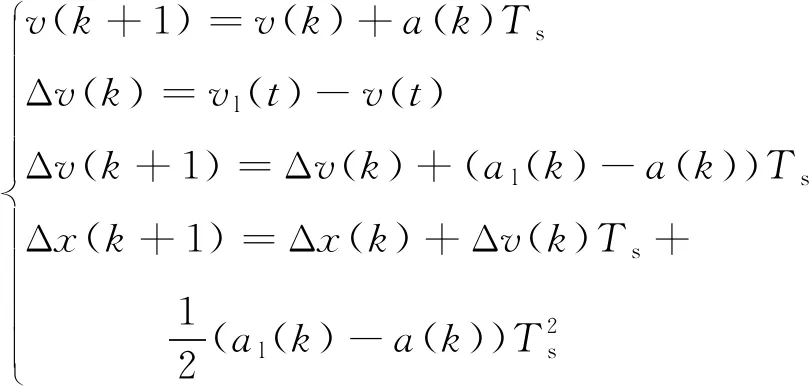
(13)

式中:vl(k)、v(k)、al(k)、a(k)、Δv(k)、Δx(k)分别表示k时目标车的车速、主车车速、目标车加速度、主车加速度、主车与目标车的速度差、主车与目标车的距离差，Ts为采样时间，vl(k+1)、Δv(k+1)及Δx(k+1)分别表示k+1时刻目标车的速度、主车与目标车速度差、主车与目标车的距离差。

由于车辆控制系统的非线性较强，上层控制器与下层控制器之间存在一定的迟滞，则将实际的加速度与期望的加速度关系表示如下：

(14)

式中:τ为惯性时间常数，u(k)为求解的期望加速度。

为了使上层控制器的求解效果更加准确，本文将主车的加速度变化率引入到到车辆纵向运动学模型之中。由离散差分原理求解主车的加速度变化率表示如下，其中j(k+1)表示主车的加速度变化率。

(15)

则可以将式(13)转化为：

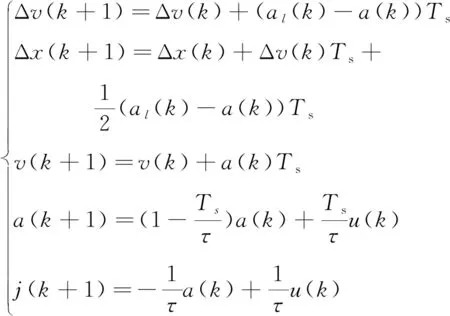
(16)

选取x(k)=[Δx(k) Δv(k)v(k)a(k)j(k)]T为控制系统的状态变量，主车的期望加速度μ(k)为控制变量，前车的加速度为al(k)扰动变量，y(k)=[δ(k) Δv(k)a(k)j(k)]T为系统的输出变量，则建立车辆纵向运动学模型的状态空间表达式：

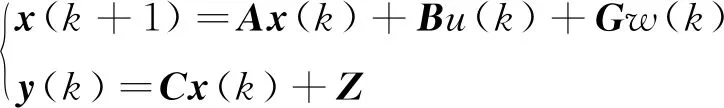
(17)

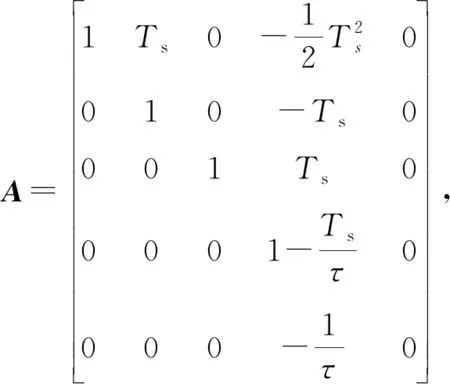
2) 控制目标分析

为了兼顾车辆巡航跟车时安全性、舒适性、跟车性等多方面的要求，将控制目标转化为相应的目标函数。

安全性：在巡航行驶中需要满足相应的法规要求，并避免车辆发生碰撞，将车辆的行驶实际速度和车间距约束如式(18)，式中d0为避免发生碰撞的最小安全距离，vmin和vmax分别为满足交通法规约束的车辆速度上下限。

Constraints: Δx(k)>d0,vmin≤v(k)≤vmax

(18)

舒适性：一般利用车辆加速度和加速度变化率衡量驾驶舒适性，对其约束为：

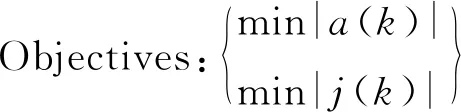
(19)

Constraints:amin≤a(k)≤amax,jmin≤j(k)≤jmax

(20)

式中amin、amax、jmin、jmax分别为加速度及加速度变化率的最小值、最大值。

跟车性：为满足车辆跟车时的动态响应，车辆期望的车间距和实际车间距的误差δ(k)应趋于0，实际车速与目标车的车速误差Δv(k)应趋近于0，跟车性的优化目标如下：

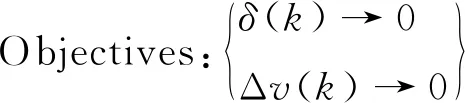
(21)

3) 多目标MPC控制器设计

基于已经建立的车辆纵向运动学模型的状态空间表达式，设定ξ(k)=[x(k)μ(k-1)]T，则可得：

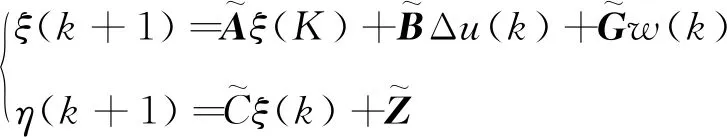
(22)

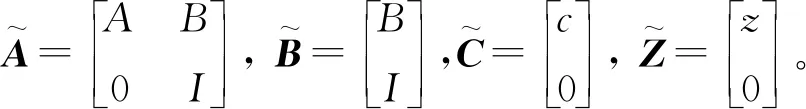
Y(t)=ΨtX(t)+ΘtΔU(t)+ΥtW(t)+Z

(23)

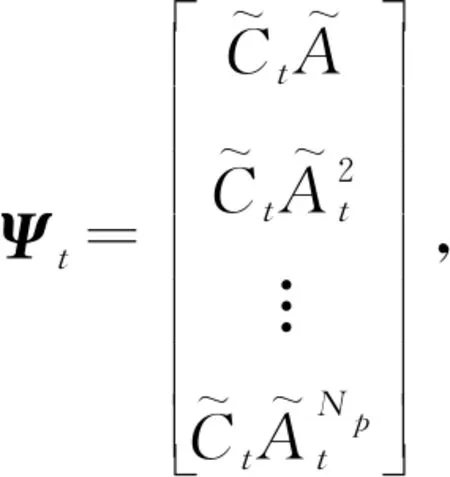
基于多控制目标约束和优化指标，建立目标函数如下：

(24)

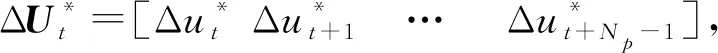
1.2.4换道轨迹规划

换道是车辆运动控制的常规操作之一，主要包括强制换道和自由换道[19]。强制换道一般发生在危险驾驶、匝道、汇流等交通场景，自主换道一般是由于驾驶员不满意当前车道的行车速度追求更高的行车速度及驾驶习性所致。因此，本文主要针对自主换道行为进行换道轨迹规划及轨迹跟踪控制器设计。

轨迹规划是实现车辆换道的关键，目前常用的轨迹规划方法有图搜索、随机采样、几何曲线、基于动态优化等方法，其中几何曲线中的五次多项式规划方法具备结构简单、曲线曲率连续且平滑、不存在阶跃等优点被广泛应用。

多项式曲线利用车辆换道起点、终点位置和姿态信息可得到满足换道的参考轨迹曲线，五次多项式的表达式如下：

y(x)=a5x5+a4x4+a3x3+

a2x2+a1x+a0

(25)

式中，a0～a5为五次多项式的系数，其可由下式求解得到。

(26)

式中:x0、y0、x1、y1分别表示车辆换道的初始位置和终止位置。

1.2.5轨迹跟踪控制

轨迹跟踪控制是实现车辆换道的关键，本文采用兼顾多目标约束及优化的MPC算法进行轨迹跟踪控制器的设计。

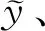
(27)

其中H=

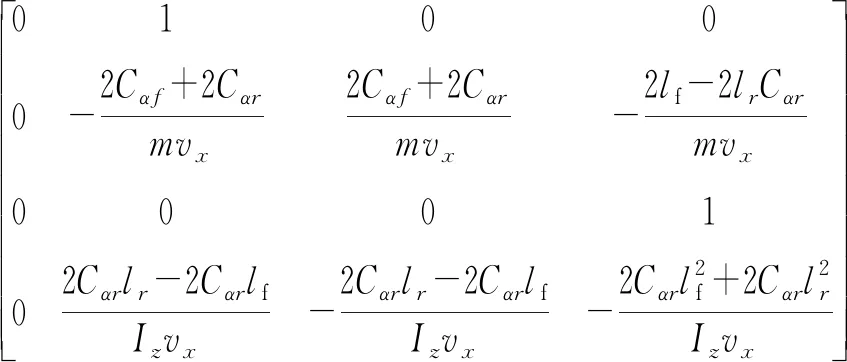
基于上述建立的状态空间方程，本文将其转化为M脚本，利用Matlab中的MPC Designer工具箱设计适用于换道的MPC控制器。定义MPC控制器的输入及输出结构、控制器参数、约束条件等即可完成MPC控制器的设计。通过多次调参与仿真测试设定预测时域为30、控制时域为20、采样时间为0.01,控制约束为-0.5 rad≤δ≤0.5 rad。

2 仿真测试与结果分析

利用Prescan/Carsim/Simulink软件进行联合仿真测试，其中车辆动力学模型部分参数如表1所示。

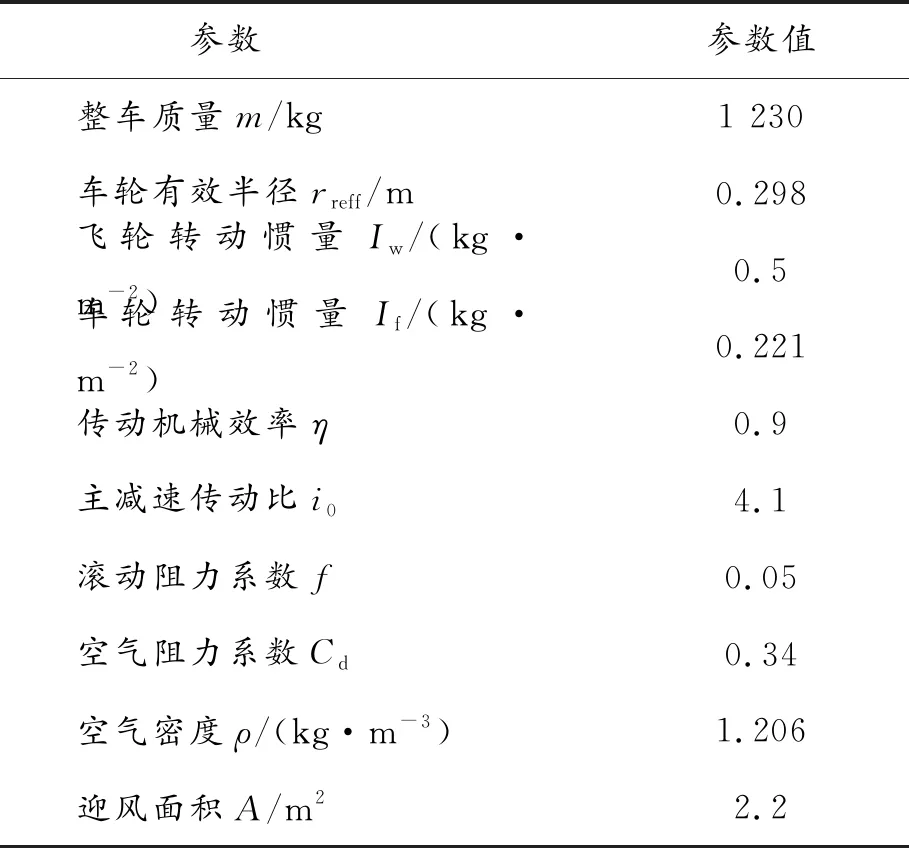
表1 车辆动力学模型部分参数

为验证本文设计的具有换道功能的自适应巡航控制策略，分别设计了定速巡航、定速巡航-跟车巡航、定速巡航-跟车巡航-换道巡航3类工况进行仿真测试。另外，为了验证多控制模式切换策略，并便于对结果进行分析，分别用数字‘1’‘2’‘3’代表定速巡航、跟车巡航、换道巡航模式。

2.1 定速巡航工况

定速巡航工况中主车前方不存在目标车辆，车辆将根据驾驶员设定的车速巡航行驶，本文设计了2种工况进行仿真测试,主要验证ACC车辆对设定巡航车速的响应。

工况一：主车的初始速度为40 km/h，前方不存在目标车辆，设定期望巡航车速从40 km/h等速递增至120 km/h，仿真测试结果如图7所示。

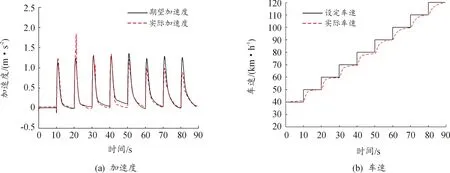
图7 定速巡航工况一仿真测试结果

工况二：主车的初始速度为120 km/h，前方不存在目标车辆，设定期望巡航车速从120 km/h等速递减至40 km/h，仿真测试结果如图8所示。

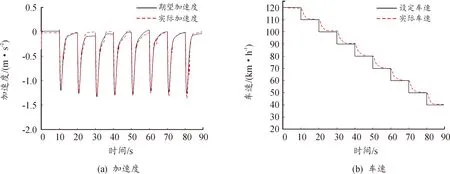
图8 定速巡航工况二仿真测试结果

根据图7和图8的仿真测试结果分析可知，ACC车辆对设定的期望巡航车速响应较好，可满足定速巡航的功能要求。

2.2 定速巡航-跟车巡航工况

定速巡航-跟车巡航工况中，当主车前方存在目标车辆时，主车将跟随前车稳定行驶。本文设计了复合工况进行仿真测试，主要验证ACC车辆定速巡航-跟车巡航控制模式切换及跟车行驶的稳定性等。

设定主车的初始车速为40 km/h，巡航车速为80 km/h；主车前方250 m处存在目标车，目标车初始车速为36 km/h，在50、86 s时目标车车速分别增加至72、108 km/h，仿真测试结果如图9所示。

根据图9中仿真测试结果分析可知，初始时刻主车前方不存在目标车辆，车辆执行定速巡航模式并迅速响应设定的巡航车速80 km/h。在6.2 s时主车检测到存在目标车辆，执行跟车巡航模式，19 s时主车跟随目标车辆以36 km/h的车速稳定行驶。在50 s时目标车车速增加至72 km/h，主车响应目标车的动态变化以72 km/h的车速稳定跟车行驶。在86 s时目标车车速增加至108 km/h逐渐远离主车，主车车速从72 km/h增加至80 km/h，并在99 s时执行定速巡航模式。综合仿真测试结果可知，ACC车辆在定速巡航-跟车巡航时的控制效果较好。

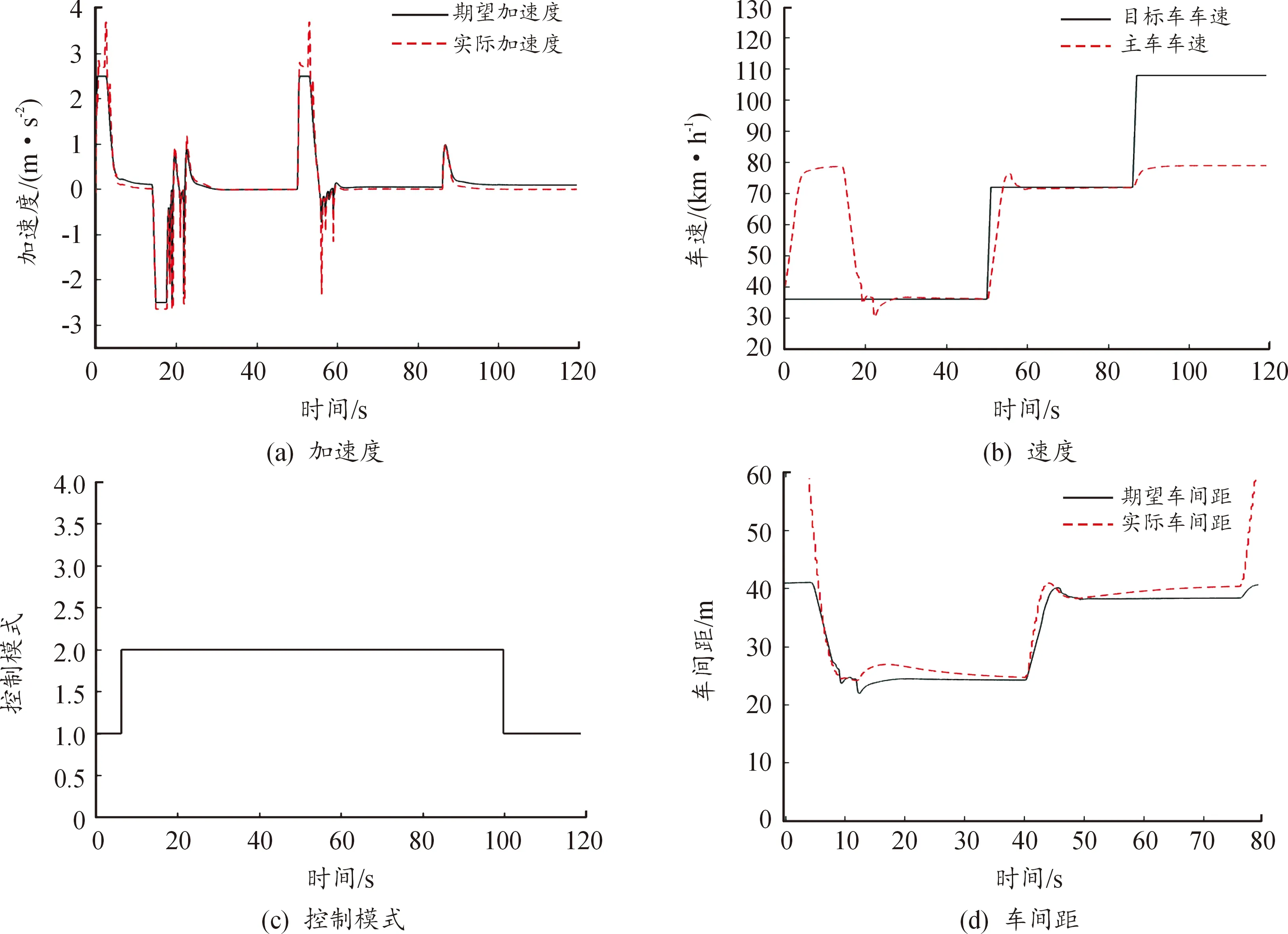
图9 定速巡航-跟车巡航工况仿真测试结果

2.3 定速巡航-跟车巡航-换道巡航工况

定速巡航-跟车巡航-换道巡航工况中主车前方存在低速行驶目标车辆且当速度不满意累计度大于阈值时，主车将主动控制车辆进行换道以追求更高的行驶速度。本文设计多复合工况进行仿真测试，主要验证ACC车辆的多模式切换、换道功能激活及自主换道等。

设定主车的初始车速为40 km/h，巡航车速为80 km/h；主车前方250 m处存在目标车，目标车初始车速为54 km/h，并保持该车速稳定行驶，仿真测试结果如图10、图11所示。

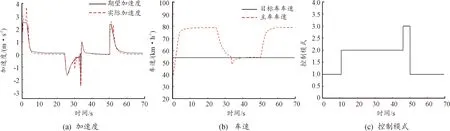
图10 纵向控制仿真测试结果

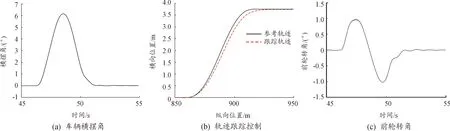
图11 横向控制仿真测试结果

根据图10中的仿真测试结果可知，初始时刻主车前方不存在目标车辆，车辆执行定速巡航模式并迅速响应设定的巡航车速80 km/h。在10.7 s时主车检测到存在目标车辆，执行跟车巡航模式，32 s时主车跟随目标车辆以54 km/h的车速稳定行驶。在46 s时速度不满意累计度大于设定的阈值执行换道巡航模式，换道结束后主车前方不存在目标车辆执行定速巡航模式，50 s时主车迅速响应设定的期望车速巡航行驶。根据图11中横向控制的仿真结果可知，主车可稳定跟踪规划的参考轨迹且前轮转角控制量及状态量横摆角均在合理的范围。

PreScan软件中的VisServer可对仿真过程中的视频进行回放，本文利用其Replay模块将ACC车辆自主换道时的状态展示于表2，其中t表示仿真时间。

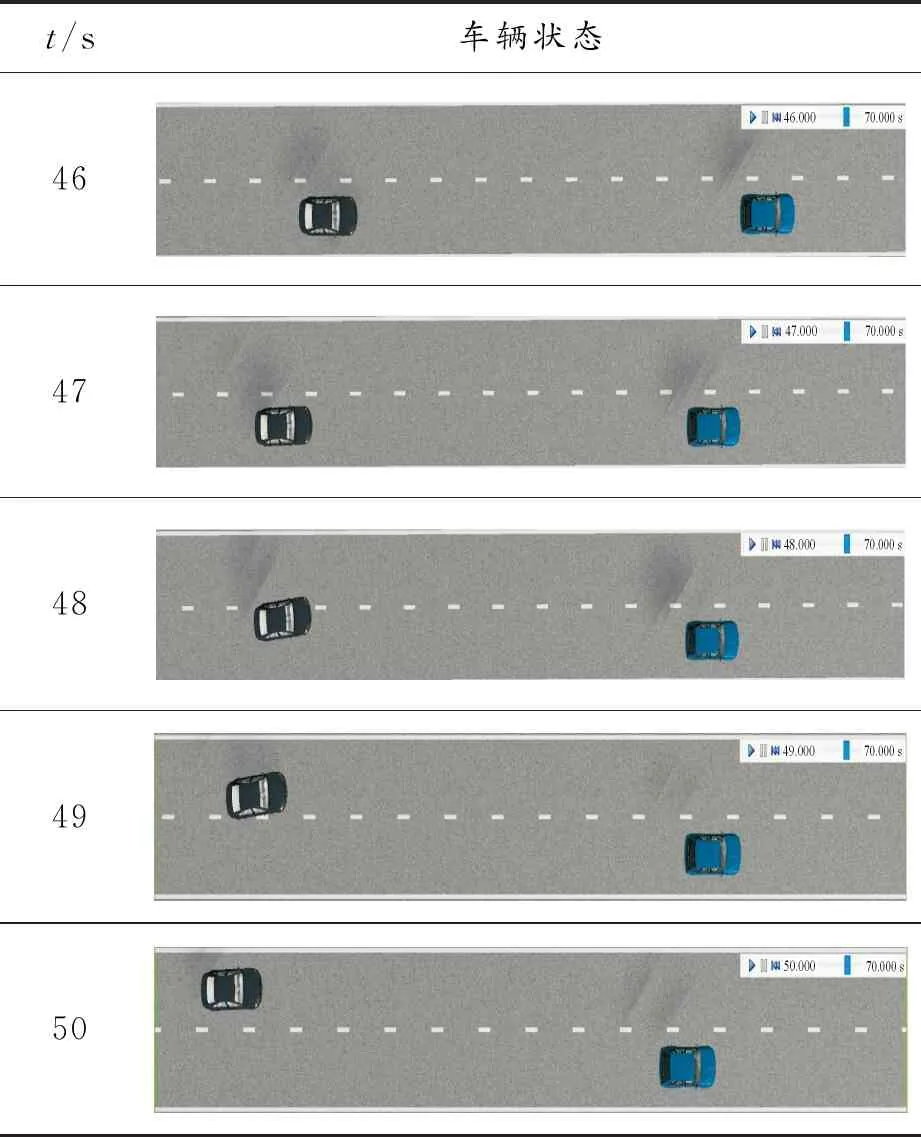
表2 ACC车辆换道状态

3 结论

本文设计了具有换道功能的自适应巡航控制策略，当ACC车辆在面对前方低速行驶的目标车辆时可执行换道操作，其可有效地提高ACC车辆的行车效率。首先，将ACC车辆的控制模式分为定速巡航、跟车巡航、换道巡航3种，并基于速度不满意累计度设计了多模式切换策略。然后，采用分层式控制结构，基于MPC算法设计了自适应巡航控制器和轨迹跟踪控制器，基于五次多项式进行了换道轨迹规划等。最后，利用Prescan/Carsim/Matlab软件进行了联合仿真测试。

由仿真测试结果可知，本文设计的具有换道功能的自适应巡航控制策略在定速巡航模式下可按照设定的车速稳定行驶；在跟车巡航模式下可跟随前车稳定巡航，响应快速且鲁棒性较好；在换道巡航模式下可稳定跟踪规划的参考轨迹实现自主换道。另外，ACC车辆可按照设计的多模式切换策略进行模式切换。本文设计的控制策略及控制器稳定、高效且可靠，可为后来的研究提供参考。本文亦存在不足之处，研究过程中未考虑不同驾驶员的驾驶特性、换道时的工况比较单一等，后续可进一步研究。