基于Voronoi分形划分的双孔径多孔材料孔道结构参数化设计

张禹，刘如铁，陈洁，熊翔，李浩，王铸博

基于Voronoi分形划分的双孔径多孔材料孔道结构参数化设计

张禹，刘如铁，陈洁，熊翔，李浩，王铸博

(中南大学 粉末冶金国家重点实验室，长沙 410083)

本文提出了一种适用于模拟双孔径多孔介质的孔道结构模型，该模型可独立形成空间均匀分布的大、小尺寸的两种孔径，并在此基础上开发可以生成参数化孔道模型图示及构成体素坐标的面向过程程序。通过划分函数的迭代，从对应几何方法的自相似性引出此模型的一般孔隙度、分形维度、间隙度和比表面积方面的讨论。最后通过面向对象编程，选择工业三维建模软件开发一种可以生成较大规模几何模型文件的技术路线及渗流与电化学仿真应用方法。

Voronoi划分；分形；二元孔隙度；孔道结构；多孔介质；多孔电极

多孔材料中孔隙的空间分布具有随机性，孔隙连通方式和孔隙形貌构成了材料的孔道结构，所以多孔材料的孔道结构具有随机和复杂的特征。多孔材料比表面积主要由材料内部表面贡献，孔道结构连通了材料部分内外表面，外部流体可以进入孔隙中充分接触材料，因此多孔材料在石油催化、吸附分离、电化学、传热与传质方面有着广泛应用[1−4]。设计多孔材料的孔道结构有利于研究和生产过程中材料参数识别，材料性能预测以及指导新材料的研究[5−6]。

随着多孔材料的不断发展，不同应用领域对于多孔材料的孔道结构特征提出不同的要求。例如，在环路热管的应用中，多孔毛细芯所产生的毛细压力是热管内工质流动循环的关键驱动力。其中小孔贡献毛细压力，大孔贡献高孔隙度以保证良好的渗透性[7]；在多孔氧化硅骨架镍催化裂解甲烷应用中，既需要引入大孔径结构以避免积碳堵塞和促进反应物流动，也需要引入大量小孔结构提升催化剂比表面积[8]；在空气净化滤芯应用中，家用空气净化设备出于节能和过滤效能考虑，要求滤芯同时具有小孔(典型直径小于2.5 μm)保证高比表面积，从而有效吸附通过空气中的悬浮颗粒，同时利用大孔结构的高连通性降低风阻[9]。综上，对多孔材料进行微观孔道结构设计，是制备满足应用要求的高性能多孔材料的前提和基础。

当多孔材料中同时存在分别集中在不同尺寸范围的两类孔径，且两类孔径尺寸相差10倍以上时，称此类多孔材料的孔道结构为双孔径结构。双孔径结构的产生归因于其制备过程中不同的造孔机理。例如以聚氨酯发泡为模板的多孔镍材料，添加造孔剂烧结制备的镍基或铜基粉末冶金材料，添加造孔剂烧结金属毡等，其孔径分布为典型的双峰结构[10−11]，大孔径由造孔剂形成，小孔径由粉末材料在烧结过程中的多种迁移机理共同作用形成。设计双孔径结构的目的在于利用其不同大小孔隙的相互匹配，实现高比表面积与连通性、渗透性及其他多种特定应用性能的组合，而如何设计孔道结构是双孔径材料制备的前提。

目前研究者们发展了多种获得孔道结构的方法：随机几何方法、模拟沉积方法、统计学习方法，以及micro-CT扫描等[12]。随机几何方法使用二维或三维随机过程算法和输入参数对孔道结构进行建模生成，输出几何模型的统计不变量。相比其他方法，随机几何方法具有设备资源要求较低的优势[13]。Voronoi图是一种常用的随机几何方法，也是自然界中的常见现象[14]，它的概念于1907年由VORONOI完善，已经广泛用于生物学、地理学、材料科学等方向的研究[15−17]。目前研究应用Voronoi图建立双孔径孔道结构方法可总结为两类：以PVT(poisson-voronoi tessellation)为代表的调节Voronoi生成点空间分布方法和以LVT(laguerre-voronoi tessellation)为代表的度量空间算法。本研究分析以上两种算法在构建双孔径结构的孔隙空间分布和数量分布的不足，从一种二维的Voronoi分形划分的概念获得启发[18]，提出一种以三维Voronoi划分迭代地构造双孔径材料孔道结构的方法，如图1。

考虑到两次划分迭代产生的自相似特性，本研究分析推导了估算迭代PVT的孔隙度、分形维度、比表面积和间隙度的公式。其次，编写输出孔道结构的迭代算法，并且借助常用的数学建模及工业软件，开发一种生成模型文件的技术路线。最后，将程序输出的模型作为计算域，展示了本研究提出的模型在渗流仿真和电化学仿真应用的可行性。

1 Voronoi划分与孔道结构

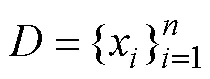
图1 双孔径模型生成顺序图

(a) Cylindrical region; (b) Poisson points in cylindrical region; (c) Voronoi tessellation based on poisson points; (d) Zoom-in on a thin square for observation; (e) Second order cylindrical region; (f) Voronoi tessellation in each second order cylindrical region

设置PVT的泊松强度为空间位置的函数，形成生成点强度的各向异性分布，从而可以调整生成点的密度，造成PVT单胞的聚集和离散，形成PVT二元孔径分布。然而这种结构孔隙空间分布继承了生成点强度的空间各向异性，因此双孔径结构模型呈各向异性，不符合双孔径孔道结构两种孔隙分别空间均匀分布的特征。

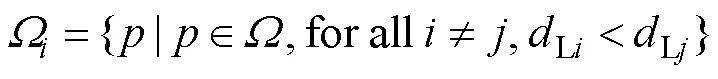
对比孔隙尺寸集中单峰分布的氧化铝泡沫，LVT模型在单胞体积、单胞面的数目、单胞棱边数目上都非常接近实际材料，但是LVT目前无法表征双孔径多孔材料的孔道结构，原因是LVT的生成点来自分子动力学模型混合的堆积球体，球体在扰动的边界条件下充分混合，形成致密且随机的堆积。如使用LVT方法进行双孔径模型建模，需要同时引入尺寸对应双峰分布的球体，然而尺寸差异较大的颗粒难以在振动力场下混合均匀[23]，造成LVT无法形成两种尺寸独立分布的随机球体填充。

借助以往研究者对PVT模型参数化形成特定孔隙度的成果[24]和一种二维Voronoi迭代随机几何图形的算法设计[18]，考虑到双孔径材料大孔和小孔的形成机理的独立性，首先将总孔隙度total分配为由大孔形成的部分1和小孔形成的部分2，对应实际测量双孔径材料块体的孔隙度和压汞法获得的孔径分布，如式(2)：

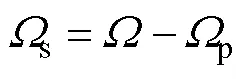
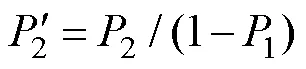
WEJRZANOWSKI等[21]总结了多种验证多孔模型的孔隙度公式，LEI等[25]从规则晶格划分出发开发了孔隙度公式，并且实现了孔道结构的梯度变化。本文利用LEI等开发的式(4)，调整随机点的数量和棱边纤维设置的半径，获得多孔模型孔隙度，其中C为高阶修正项，为正方体空间的边长。

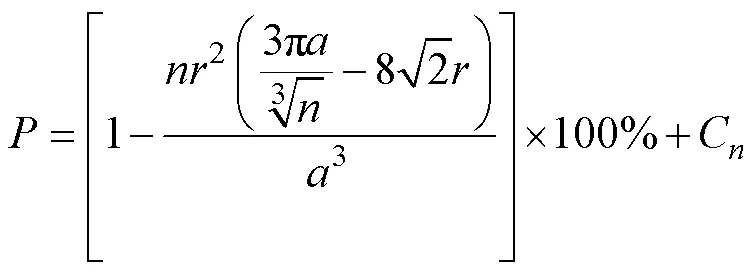
2 算法

2.1 二阶Voronoi划分

为了减少式(4)的变量数目，考虑到Voronoi划分适用的空间不限于其形状，本文认为式(4)的边长参数可以推广定义为与空间体积相等的正方体边长，记的体积为V，可得式(5)。

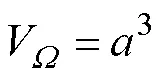
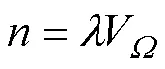
将式(5)和式(6)代入式(4)并忽略高阶修正项，得总孔隙度，如式(7)：

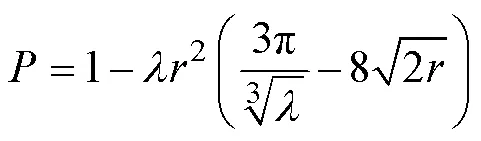
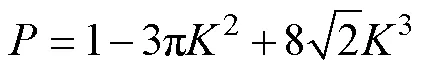
记第一阶划分的泊松点集强度参数为λ1，设置纤维半径为1，第二阶划分的泊松点集强度参数为2，设置纤维半径为2。代入式(2)、式(3)、式(8)，得到式(9)，其中=1,2。

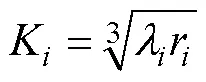
研究实验中通常可以获得两种孔径尺寸d的数值[8, 10]，本文以每阶划分形成的单胞体积v代表单个孔隙体积，孔径尺寸d为等效球形孔隙直径，如式(10)。而划分产生在空间Ω中的平均孔隙总数与生成点数n相等，结合式(6)，可得式(11)。

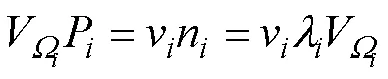
由式(10)和式(11)得式(12)，即每阶划分产生的孔隙度P、孔径d与输入泊松强度λ的关系，结合式(9)解出建立二阶PVT模型需要的所有参数。

2.2 模型图示

UHLMANN[26]指出目前Voronoi划分的学术研究通常使用Matlab或“VORO++”的函数库，两种方法都提供了运行时间与生成点规模成线性关系的快速算法。本研究第二次划分的空间位置由第一次划分的棱边决定，需要对大量坐标进行平移、投影和旋转，因而选用Matlab作为向量编程的工具。表1所列为多阶划分算法主函数的伪代码，图2所示为分别调整大孔与小孔泊松点集强度生成的双孔径模型，可见本文算法具有独立调整两种孔径分布的功能。

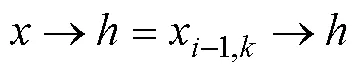
2.3 分析

2.3.1 孔隙度

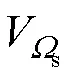
表1 生成N+1阶划分算法的伪代码

表2 投影法处理圆柱区域边界算法的伪代码

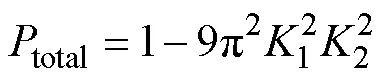
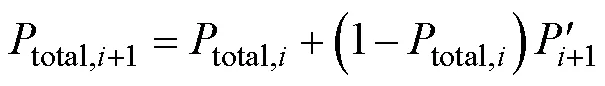
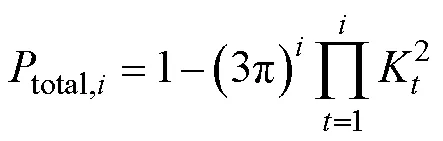
2.3.2 分形维度

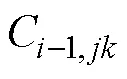
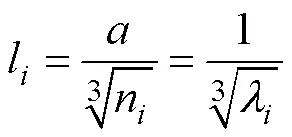
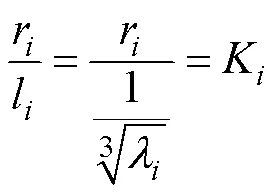
由式(16)、(17)可知式(13)中的参数为平均化圆柱空间的半径与长度的比值。

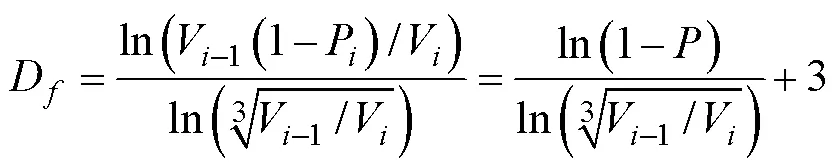
在初始圆柱长度为单位长度时，代入几何相似式(9)和式(14)，式(18)可化简为式(19)和式(20)：

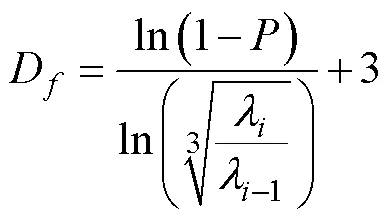
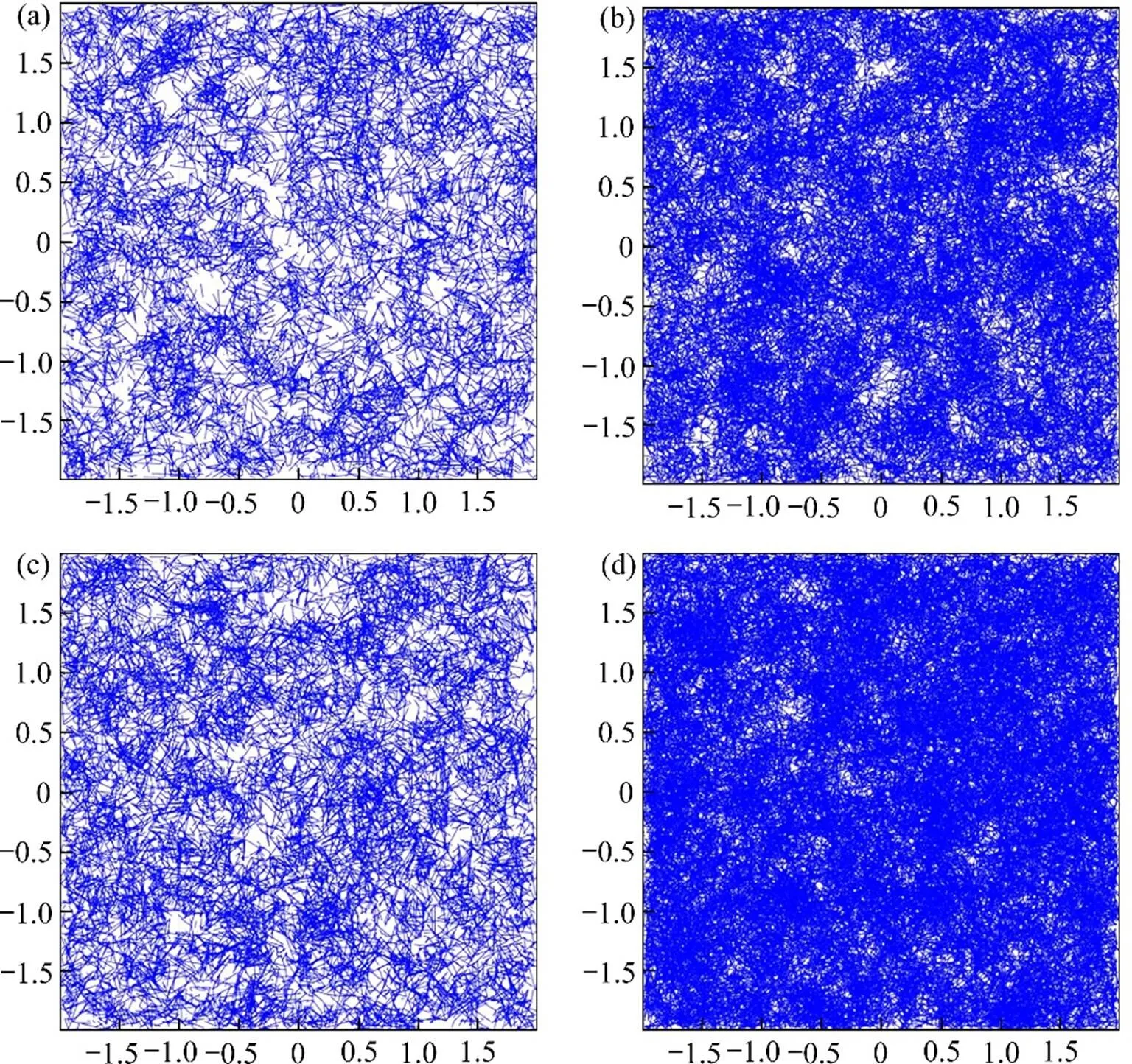
图2 相对厚度为0.5不同泊松强度下形成的大小孔模型双孔隙度图示

(a) 30, 300; (b) 30, 600; (c) 60, 300; (d) 60, 600

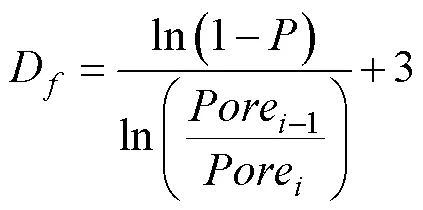
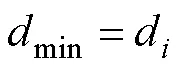
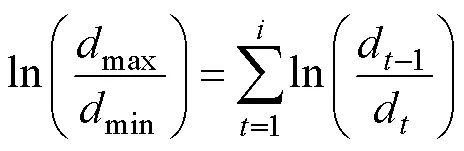
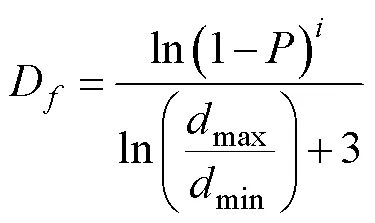
将式(2)，式(3)推广至多峰分布，可得孔隙度组成的级数形式，如式(23)。将式(23)代入式(22)得到(24)：

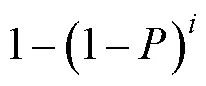
WEI等[28]研究了分形几何方法推导的毛细孔径分布，如式(25)。式(24)与式(25)存在差别的原因是WEI的分形方法为迭代地划分孔隙，本研究的方法为迭代地划分实体，两种方法关于孔隙相-实体相对称。

从式(25)获得按幂次分布的孔径密度分布函数，将此函数与泊肃叶流动压降进行积分，得到预测的Kozeny-Carman数值与乳液渗流实验结果相符[28]。式(24)证明Voronoi分形划分方法可以获得幂次分布的孔径，所以式(18)～(24)分析得到的分形维度可用于双孔径模型的流体分析。

由于泊肃叶流动将复杂的孔道近似为平行的圆柱流道，所以研究者引入屈曲度，孔道分形维度等几何不变量改善精度，这些几何不变量代表相应测量的数值与分辨率的变化规律，一般以Hausdorff“数格子”的方法获得。在向量编程环境中将待处理的模型所在空间网格化，然后判断每一格点与模型的相交状态，例如使用Matlab内建函数find()，可以提取待计数的格点。

2.3.3 间隙度

间隙度是衡量聚集和不均匀性的物理量[29]，XIA等[30]使用算法生成二维孔隙图形并以LBM(lattice Boltzmann method，格子玻尔兹曼方法)分析了其渗透系数，结果表明对于固定的孔隙度，渗透系数以正幂次规律与间隙度正相关，与分形维度负相关[30]。此结论也印证了双孔径材料引入较大孔径增加传质能力的机理，即在介观尺度下改变材料的间隙度。

计算间隙度的数值需首先设置位于模型内边长为的立方体窗格空间Box()，滑动窗格并获取窗格空间的孔隙度Box，一般将滑动窗格网格化并设置格点采样阈值，所以Box为离散型数值，记滑动窗格次统计Box对应的频率为(Box,)，则间隙度(Box,)由式(26)计算[29]。

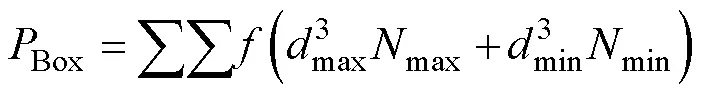
2.3.4 比表面积

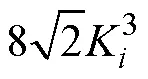
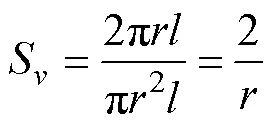
需注意的是，采用式(28)估算实际材料比表面积需另外考虑材料孔道内表面粗糙度的贡献。

3 模型实现及应用

3.1 几何模型

所有输入体素的并集，对应建模软件的布尔求和运算。虽然目前存在可以与数值分析软件交互的三维建模工具，如COMSOL Multiphysics，Ansys APDL 等[5, 19−20, 24]，但是其交互的稳定性尚待提高。当绘制体素数高于1 000时，在内存有限的桌面级电脑上，无论是修改几何文件容差还是分步存储，建模进程都难以保证平稳运行。本文选用Solidworks在.NET环境中与Excel进行交互，Excel来自预先存储的Matlab所输出的坐标矩阵，在逐条读取坐标的同时，.NET环境调用Solidworks程序进程在相应文件中形成体素，循环至所有体素创建完毕后保存文件，可有效保证交互的稳定性。

将面向过程的矩阵运算与面向对象的建模过程独立编程，可显著提升效率和程序稳定性。实时呈现运算图示可预先发现建模的错误，将坐标数据预先存储在散列表文件中可以节约运行内存，集中计算资源运行体素搭建。

体素搭建是一个循环输入体素并与既有体素布尔求和的过程。本文采用向Solidworks输入临时体(一种按参数形成的body类型)的方式输入体素，再转换临时体为壳体(surface类型)，最后填充壳体获得实心圆柱体，完成体素输入。执行填充时设置merge为True，即可在输入体素的同时自动布尔求和，上述调用函数均如图3所示。

在2016版本后Solidworks不再限制多实体零件文件的实体数上限，此功能强力支持了多孔体的孔道结构设计，并且.NET环境所支持的语言如VB.NET，C#，C++都可以将每个体素的建立加入Try-Catch语句，增加程序的健壮性，避免某次体素建立失败导致程序崩溃。

3.2 仿真应用

以有限元或有限体积方法为例，多孔介质的渗流模拟通常需要耗费巨大的计算资源，且计算域复杂的几何形状会导致极其复杂的网格划分，又需要耗费人力进行网格调整和优化。因此，LBM因其易于编程部署，适用并行计算，前后处理难度低，适合低速流动分析的特点被广泛应用于微流动仿真分析领域。本文介绍一种通过图像处理方法将三维模型再次压缩为二维图形，可以达到继续简化计算规模且能得出定性结论的目的。如图4(a)，黑色区域为通过图像处理采集三维薄片得到的多孔介质实体部分，蓝色区域为流体的计算域，蓝色的深浅代表LBM运行4 000周期该处的无量纲流速，从而根据实际的雷诺数估计相应多孔介质的渗流性能。可见本案例中，高流速集中在大孔区域的喉部，根据泊肃叶定律层流压降正比于流速的估计，这与研究多孔介质压降的直观经验相符。

同时，压缩三维模型得到的二维图形同样可以应用于电化学仿真分析，在不考虑电解质流动和宏观离子浓度变化时，使用有限元或有限体积法进行电流密度计算相比流体力学仿真更加快速。如图4(b)所示，红色线代表电解质中的电流密度线，可见电流密度分布取决于计算域的几何形状。

本研究开发的多孔模型可应用于三种简化假设的电化学分析模型：

1) 考虑溶液整体不存在活性离子浓度梯度，电解液在恒稳电压下表现为电阻。此应用输出上述电流密度线和电势等势面，可用于优化电解池整体效率。

2) 考虑电极表面存在浓差极化和双电层电容，结合本研究模型，可以进行循环伏安或电化学阻抗谱等分析。例如可通过提高小孔生成强度，提升模型比表面积，影响双电层电容数值。

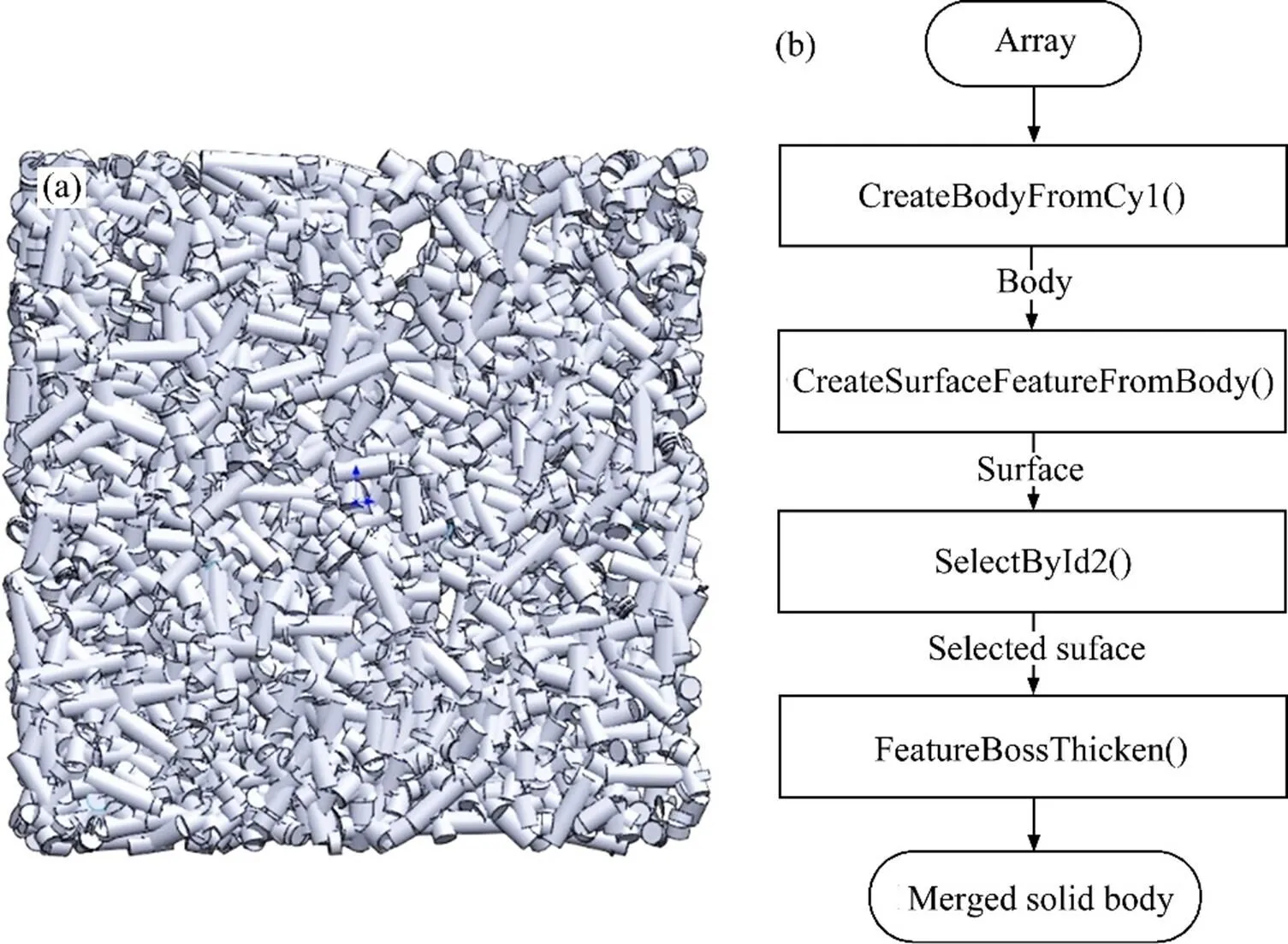
图3 一个3746体素的多实体SLDPRT型文件(a)及Solidworks内建函数调用流程(b)

图4 使用格子玻尔兹曼方法渗流分析(a)及电化学模拟电解质中多孔电极产生的电流密度分布(b)

3)考虑电解液存在流场，且存在非活性离子支持迁移电流，结合LBM在同一几何计算域的流速分布结论，可实现流体力学和活性离子物质传递的耦合，从而将电化学反应还原为浓度依赖动力学，实现在流动电解质中多孔电极的电化学仿真，即完整描述Nernst-Plank物质传递方程。

4 结论

1) 迭代PVT方法可实现双孔径模型的大孔和小孔的尺寸分布独立，同时保持空间分布均匀。通过控制每次迭代输入参数可输出具有期望孔隙度、分型维度、比表面积和间隙度的模型。

2) 使用Solidworks API可构建本研究模型的实体文件，且实体文件包含的体素数具有较复杂的规模。使用Matlab图形模块可以处理本研究模型的二维 投影。

3) 应用LBM方法可实现分析本研究模型的多孔介质渗流仿真。在ComsolMultiphysics环境中利用本研究模型可进行多孔电极表面电化学分析。后续研究可实现相同模型计算域在不同仿真环境和多种物理场条件下的耦合仿真。

[1] FOROOZESH J, KUMAR S. Nanoparticles behaviors in porous media: application to enhanced oil recovery[J]. Journal of Molecular Liquids, 2020: 113876.

[2] DIAO K K, ZHAO Y Y. Heat transfer performance of sintered Cu microchannelsproduced by a novel method[J]. International Journal of Heat and Mass Transfer, 2019, 139: 537−547.

[3] EGOROV V, O'DWYER C. Architected porous metals in electrochemical energy storage[J]. Current Opinion in Electrochemistry, 2020, 21: 201−208.

[4] WOOD S, HARRIS A T. Porous burners for lean-burn applications[J]. Progress in Energy & Combustion Science, 2008, 34(5): 667−684.

[5] NIE Z W, LIN Y Y, TONG Q B, et al. Numerical investigation of pressure drop and heat transfer through open cell foams with 3D Laguerre-Voronoi model[J]. International Journal of Heat & Mass Transfer, 2017, 42(2): 969−974.

[6] LOTFI N, FARAHANI T S, YAGHOUBINEZHAD Y, et al. Simulation and characterization of hydrogen evolution reaction on porous NiCu electrode using surface response methodology[J]. International Journal of Hydrogen Energy, 2019, 44(26): 13296−13309

[7] LIU R T, CHEN J, XIONG X. Influence of porogen type and copper powder morphology on property of sintering copper porous materials[J]. Journal of Central South University, 2018, 25(9): 2143−2149.

[8] TANGGARNJANAVALUKUL C, DONPHAI W, WITOON T, et al. Deactivation of nickel catalysts in methane cracking reaction: effect of bimodal meso–macropore structure of silica support[J]. Chemical Engineering Journal, 2015, 262:364−371.

[9] FU X W, LIU J J, DING C F, et al. Building bimodal Structures by a wettability difference-driven strategy for high- performance protein air-filters[J]. Journal of Hazardous Materials, 2021, 415(42): 125742.

[10] LI H, LIU R T, CHEN J, et al. Preparation of nickel porous materials by sintering nickel oxalate and sodium chloride after blending and reduction[J]. Journal of Materials Research and Technology, 2020, 9(3): 3149−3157.

[11] WANG Z B, CHEN J, LIU R T, et al. Preparation of an ultrafine nickel powder by solid-phase reduction with a NaCl separator agent[J]. Advanced Powder Technology, 2020, 31(8): 3433−3439.

[12] AL-KHARUSI A S, BLUNT M J. Network extraction from sandstone and carbonate pore space images[J]. Journal of Petroleum Science and Engineering, 2007, 56(4):219−231.

[13] SURI S. Handbooks in Operations Research and Management Science[M]. Amsterdam: IGI Global, 1995: 425−479.

[14] MEBATSION H K, VERBOVEN P, VERLINDEN B E, et al. Microscale modeling of fruit tissue using Voronoi tessellations[J]. Computers and Electronics in Agriculture, 2006, 52(1/2):36−48.

[15] HAN N, GUO R. Two new Voronoi cell finite element models for fracture simulation in porous material under inner pressure[J]. Engineering Fracture Mechanics, 2019,211:478−494.

[16] GATSONIS N A, SPIRKIN A. A three-dimensional electrostatic particle-in-cell methodology on unstructured Delaunay–Voronoi grids[J]. Journal of Computational Physics, 2009, 228(10): 3742−3761.

[17] MISTANI P, GUITTET A, POIGNARD C, et al. A parallel Voronoi-based approach for mesoscale simulations of cell aggregate electropermeabilization[J]. Journal of Computational Physics, 2019, 380: 48−64.

[18] SHIRRIFF K. Generating fractals from Voronoi diagrams[J]. Computers & Graphics, 1993, 17(2):165−167.

[19] XIAO F, YIN X L. Geometry models of porous media based on Voronoi tessellations and their porosity–permeability relations[J]. Computers & Mathematics with Applications, 2016, 72(2): 328− 348.

[20] CAO B W, WANG S L, WEI D, et al. Investigation of the filtration performance for fibrous media: coupling of a semi-analytical model with CFD on Voronoi-based microstructure-Science Direct[J]. Separation and Purification Technology, 2020, 251:117364.

[21] WEJRZANOWSKI T, SKIBINSKI J, SZUMBARSKI J, et al. Structure of foams modeled by Laguerre-Voronoi tessellations[J]. Computational Materials Science, 2013, 67: 216−221.

[22] NIE Z W, LIN Y Y, TONG Q B. Modeling structures of open cell foams[J]. Computational Materials Science, 2017, 131: 160− 169.

[23] KHALA M J, HARE C, WU C Y, et al. Density and size-induced mixing and segregation in the FT4 powder rheometer: an experimental and numerical investigation[J]. Powder Technology, 2021, 390: 126−142.

[24] LIU W, TANG G H, SHI Y. Apparent permeability study of rarefied gas transport properties through ultra-tight Voronoi porous media by discrete velocity method[J]. Journal of Natural Gas Science and Engineering, 2020, 74: 103100.

[25] LEI H Y, LI J R, XU Z J, et al. Parametric design of Voronoi-based lattice porous structures[J]. Materials & Design, 2020, 191:108607.

[26] UHLMANN M. Vorono tessellation analysis of sets of randomly placed finite-size spheres[J]. Physica A: Statistical Mechanics and its Applications, 2020, 555: 124618.

[27] HENDERSON N, BRÊTTASJC, SACCO W F. A three- parameter Kozeny–Carman generalized equation for fractal porous media[J]. Chemical Engineering Science, 2010, 65(15): 4432−4442.

[28] WEI W, CAI J C, XIAO J F, et al. Kozeny-Carman constant of porous media: insights from fractal-capillary imbibition theory[J]. Fuel, 2018, 234: 1373−1379.

[29] PINTO E P, PIRES M A, MATOS R S, et al. Lacunarity exponent and Moran index: acomplementary methodology to analyze AFM images and its application to chitosan films[J]. Physica A: Statistical Mechanics and its Applications, 2021, 581: 126192.

[30] XIA Y X, WEI W, LIU Y, et al. A fractal-based approach to evaluate the effect of microstructure on the permeability of two-dimensional porous media[J]. Applied Geochemistry, 2021, 131: 105013.

Parametric design of bimodal porosity structure based on Voronoi polygons and fractals

ZHANG Yu, LIU Rutie, CHEN Jie, XIONG Xiang, LI Hao, WANG Zhubo

(State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China)

This research proposed a bimodal porosity structure type providing the ability to individually form evenly distributed pores of two separated sizes. A method of generating structures parametrically was provided, and a process-oriented program was developed outputting diagrams and coordinates. Iterations of tessellation module, causing geometrical self-resemblance, were further discussed from porosity, fractal dimension, lacunarity and specific surface area aspects. Technical routes were introduced for building 3D model files of large complexity in common industrial software’s object-oriented application programming interface and applications in permeability or electrochemistry simulations.

Voronoi tessellation; fractal; bimodal porosity; porous structure; porous media; porous electrode

10.19976/j.cnki.43-1448/TF.2022007

TB113

A

1673-0224(2022)03-257-10

国家国际科技合作专项资助项目(2015DFR50580)

2022−03−23；

2022−04−20

刘如铁，教授，博士。电话：0731-88876566；E-mail: llrrtt@csu.edu.cn; 陈洁，副教授，博士。电话：0731-88876566；E-mail: chenjiecsu@163.com

(编辑 陈洁)