紧扣数学知识本质 促进学生深度学习

王火炬

深度学习区别于浅层学习，其培养目标指向培养学生的高阶思维，在情感维度方面，教师应更注重调动学生全身心参与;在具体实施策略上，教师应注重知识的系统化和结构化，采用多种手段呈现良好的课堂氛围。在数学教学中，教师要促发学生深度学习，除了根据上述两个维度实施相应的策略外，还应该紧紧扣住数学知识的本质，才能使深度学习更真切地发生，才能使数学教学不仅有效度，而且有深度和广度，最终促使学生真正获得数学知识、关键能力和核心素养。

一、引导“深究”，建构知识模型

“深究”就是要借助富有挑战性的问题情境，引导学生深入思考与探究，而在探究的过程中立足于数学思维，借助几何直观、动手操作等手段，帮助学生把生活经验抽象归纳成逻辑经验，完成从旧知识到新知识的转化，并建构知识模型。例如，在人教版三上“测量”这一单元的“厘米”相关内容的教学中，如果在课程的开始阶段就让学生拿出尺子，认识尺子上1厘米的长度，来帮助学生建立“厘米”的概念，这样的课程过于抽象和呆板，且没有抓住知识的本质。由于厘米和其他长度单位一样，本质是度量单位，因此在教学时，可以引导学生在经历度量的过程中体验和认识厘米。教师可以通过创设如下富有挑战性的问题情境形成问题串：“如下图，两条线段谁长、谁短？如何准确说出线段1比线段2长（或短）多少？你想用什么数量单位来表示这两条线段的长度？”在引导学生探索和解决一个个问题的过程中，帮助学生建立1厘米的概念。紧接着引导学生结合尺子认识2厘米、7厘米等其他长度，让学生说一说2厘米、7厘米等各表示几个1厘米，并让学生动手比划，完善“厘米”的认知。

在小学数学的课程教学中，教师应注重调动学生的多种感官，引导学生投入身心，充分体验。例如在人教版五下“质数和合数”的教学中，教师要紧紧抓住质数和合数的本质区别，借助几何直观，设置出如下具有一定挑战性的问题：“请你分别画出面积为2、3、4、5、6、7的所有长方形（边长均为整数），观察一下，说出自己的发现。”在学生动手操作和观察讨论后，引导他们归纳出结论：面积2、3、5、7的都只能画出一个长方形，它们的边长都为1和等于面积的数;4和6则不止画出一个，不仅能画出边长为1和等于面积数的长方形，还可以画出边长分别为2和2、2和3的长方形，所画出的长方形边长都是面积数的因数。随后，教师让学生再举出关于质数与合数的其他例子，进一步拓展建模，引导归纳出质数和合数的概念。如此教学，不仅渗透数形结合思想，同时紧扣知识本质，调动学生的多重感官，促进学生更好地探究知识的本质，最终形成质数和合数的概念。

二、把握“深化”，搭建知识体系

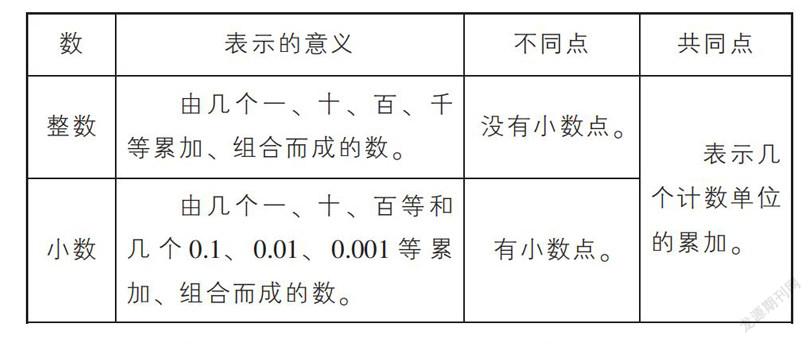
数学学科的知识之间存在着千丝万缕的联系，引导学生学习、体验知识结构，实际上是对知识学习的深化。教师应当寻找到知识间的内在联系，把相关联的知识结构化，形成知识体系，避免知识的碎片化、零散化、无序化。具体到教学中，在避免浅层建构的同时，深入挖掘知识的本质，这样搭建起的知识体系才能使学生对其理解得更加深刻。例如，在学习了人教版三下“小数的初步认识”之后，如果只是让学生认识到整数和小数的相同点都是数，不同点是小数有小数点、整数没有小数点，这样建构起来的联系未免显得浅薄。教师可以安排类似的课堂练习：“分别说出数23、456、0023、9、0.5、4.56表示几个几？请在认真思考后进行观察和分类，你有什么发现？”通过这样的练习，引导学生建立小数和整数的知识结构，即小数和整数一样，本质上都是几个计数单位的累加，最终与学生共同制成该知识结构的表格形式（如下表）。

三、指导“深解”，感悟知识的内涵外延

任何数学知识的存在都有其意义，数学知识的产生亦然。教师应注重引导学生运用最真切的感受将学到的数学知识、建构的数学模型，用于解决生活中的实际问题。在具体应用中，教师一定要抓住知识的本质，设计与知识相对应的问题让学生解决，并让其在解决过程中进一步理解和感受知识的内涵与外延，深化对知识模型的应用。如果解决问题的过程没有扣紧知识的本质，就会出现纯粹为了运用而运用或者简单套用公式的情形，使学生无法获得深刻的认知。例如，在人教版五上“植树问题”一课的教学中，笔者先引导学生通过课本中的情境建立解决植树问题的模型：总长度÷间距=间隔数，然后分三种类型建立数量关系：两端都种树用“棵数=间隔数+1”，只种一端用“棵数=间隔数”，两端都不种用“棵数=间隔数-1”。模型建立后一般要让学生运用所学模型解决实际问题，教学中如果只是按部就班地出示如下问题：“在长1千米的道路两边种树，每隔50米种一棵（两端都种），一共要种多少棵？”面对这样的问题，学生只需要机械地套用模型公式即可，并没有深入知识的本质。因此，笔者紧密结合生活实际设计出如下两道课堂练习。首先出示练习题：“在长1千米的大桥两侧安装路灯，每隔50米安装一盏，且两端都要安装，一共要准备多少盏路灯？请你说出该问题中与植树问题相对应的距离、间距、间隔数、棵树各是什么？该问题应该运用哪种植树类型？说说为什么。”待学生成功解答后，笔者接着安排另一道练习题：“木工师傅锯一段木料，锯4段用6分钟，锯成9段用时几分钟？请你尝试用植树问题的模型来解决，然后说出在该问题中与植树问题相对应的距离、间距、间隔数和植树类型。”植树问题的本质是棵数与间隔数的对应关系，教师在新课教学中应注重对该知识点的呈现，促使学生理解和掌握，在课后练习中也应进行专项训练，同时联系生活设计与生活相关的实际问题，让学生运用数学模型进行解决，从而达到举一反三的目的。又如，人教版三上“集合”一课中，其知识的本质是分类组合，特别要关注两边的类属关系，即重合部分，引导学生理解重合部分与总数之间的关系，并强调具体运用时不能重复计算。在教学进程中根据是否有重合的情况，教师可以在课件中呈现三种类型的集合图。建立集合图的模型就是要引导学生充分体验，厘清有没有重合，重合的部分是哪些。当帮助学生建立三种集合图的模型后，可以安排针对性的练习题进行课堂训练，让学生辨别可以运用哪一种集合图，说说为什么，重合的部分是什么，并说說解决问题时要注意些什么，让学生通过实际问题再次明确重合部分与总数之间的关系，以及重合部分不能重复计算的注意事项。

（作者单位：福建省厦门市同安区第一实验小学）