模拟月岩低作用力切削负载特性测试平台设计与试验验证

王祎卓，李 鹏，2，孙丽霞，李雪凇，宁宏阳

(1.北华大学机械工程学院，吉林 吉林 132021；2.燕山大学机械工程学院，河北 秦皇岛 066099)

深空探测技术是国家技术水平的综合体现.在星球探测领域，为了有效保留样品层信息，钻取采样是不可或缺的一种方式[1-4].与地质勘测相比，受真空、温度、辐射等因素限制，在月球表面钻取采样的钻进效率会大幅降低[5-8]；同时，受运载火箭能力和低重力环境的约束，月球环境下的钻进作用力较低[9-11].切削刃是破碎岩石的主要构件，切削刃破碎月岩产生的切削载荷是钻进负载的主要来源[12-13]，而切削载荷又与切削刃构型参数直接相关[14-15].因此，需要开展单个切削刃和模拟月岩力学特性研究，分析影响岩石破碎的切削刃构型参数和切削冲击参数，以便降低钻进负载，满足低作用力下月岩高效能钻进的要求.本文对单刃切削负载特性测试平台性能指标、总体方案和各个功能组件进行详细设计，研制模拟月岩低作用力切削负载特性测试平台，开展岩石单刃切削负载和冲击破碎特性试验，验证单刃与岩石相互作用力学模型和岩石冲击切削负载模型.

1 低作用力切削负载特性测试平台研制

1.1 测试平台总体方案和设计指标

模拟月岩低作用力切削负载特性测试平台的主要功能：1)开展不同切削刃参数下的切削负载试验；2)开展不同切削冲击参数下切削冲击负载试验验证.试验台三维模型及实物见图1.根据试验平台总体规划，结合月面钻进能力要求和地面钻进负载试验结果，规划模拟月岩低作用力切削负载特性测试平台设计指标，见表1.

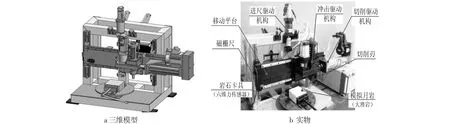
图1模拟月岩低作用力切削负载特性测试平台Fig.1Test platform for simulating low-force cutting load characteristics of lunar rock

表1 切削负载试验平台设计指标Tab.1 Design index of cutting load test platform

1.2 测试平台功能组件

模拟月岩低作用力切削负载特性测试平台组成及工作原理见图2.

切削驱动机构的功能是控制切削刃水平运动.电动缸功率Pe1=1 kW、额定负载F=1.7 kN、额定速度v1=500 mm/s、丝杠导程S1=10 mm、工作行程S2=250 mm.冲击驱动机构的功能是产生一定频率和能量的冲击力，由凸轮带动弹簧质量块提供能量.冲击驱动机构设计参数见表2.

图2模拟月岩低作用力切削负载特性测试平台组成及工作原理 Fig.2Composition and working principle of test platform for simulating low-force cutting load characteristics of lunar rock

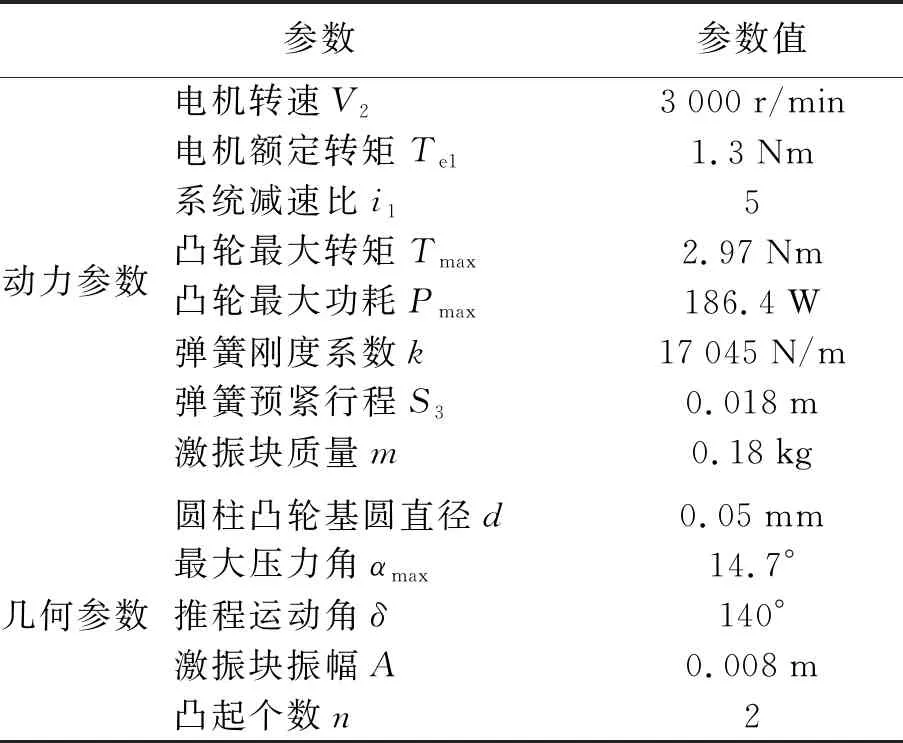
表2 模拟月岩切削负载特性试验平台冲击机构设计参数

根据表2中参数可获得冲击频率和单次冲击功：

进尺驱动机构的功能是驱动切削刃上下移动.伺服电机输出的回转运动经过滚珠丝杠副转化为直线运动，从而实现切削刃的进尺运动.进尺驱动电机额定功率Pe2=100 W，额定转速V2=3 000 r/min，丝杠导程S4=5 mm，减速器减速比i2=500∶1.

切削模拟月岩时最大进尺速度

因为切压力FPen不小于1 600 N，所以最大钻压下丝杠的回转驱动转矩

即得进尺驱动电机所需的额定转矩为

夹紧装置可以提供多切削工位.其中，六维力传感器安装在下方，x、y方向测量范围是0～±1 400 N，z轴方向测量范围是0～±3 400 N，3个方向转矩测量范围均为0～±60 Nm.

控制系统由硬件和软件两部分组成.试验过程中，数据采集卡将传感器实时采集到的运动和负载信号传输至下位机，再通过AO端口将控制指令传输给驱动器，进而控制伺服电机.上位机装有控制系统的软件部分，由MATLAB的xPC Target和Simulink控制模块实现，完成试验台各执行件的运动控制和数据采集.

图3破碎区域受力分析Fig.3Stress analysis of broken regions

2 单刃与岩石相互作用力学模型和冲击模型

2.1 单刃与岩石相互作用力学模型

2.1.1 岩石正交切削破碎模型

根据岩石切削破碎过程，将切削破碎区域划分为3个：1)剪切破碎区Ⅰ，切削力发挥主导作用，发生剪切和拉伸断裂；2)密实核压碎区Ⅱ，受切削力和切压力共同作用；3)过切削区Ⅲ，主要影响岩石切压力载荷[16].3个区域力学分析见图3.

由图3受力分析可得

其中：

对受压区域BDE进行静力平衡分析可得FT满足

上述各式参数取值见表3.

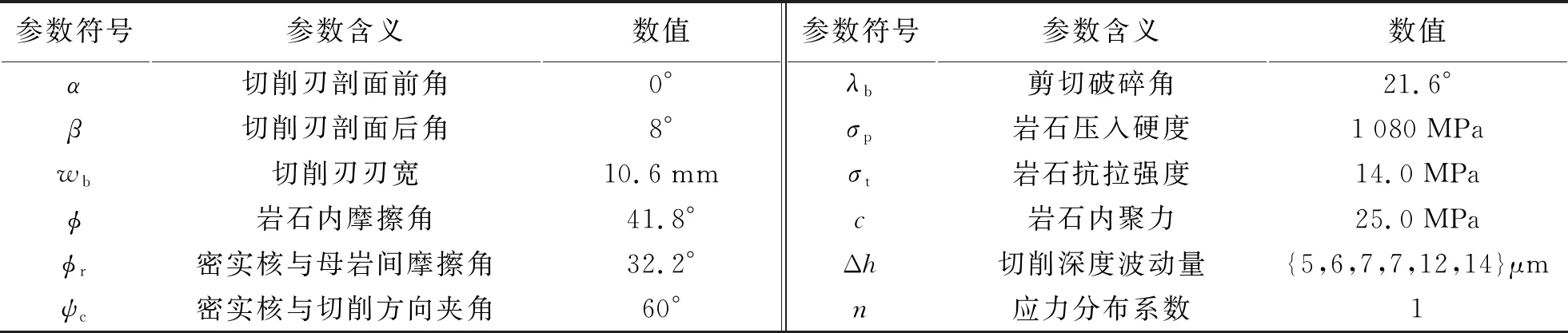
表3 切削过程中的试验参数Tab.3 Test constants in cutting process

图4模拟月岩低作用力切削负载特性随切削深度变化Fig.4Simulation of the low-force cutting load chara-cteristics of lunar rock with the change of cutting depth

将表3参数代入模型，得出切削力FCut、切压力FPen和切削深度的变化规律曲线，见图4.由图4可见，切削负载与切削深度正相关.因此，切削深度不宜过大，从而保证切削负载控制在合理范围内.

2.1.2 单切削刃负载模型

以上述模型为理论依据，考虑排屑方向后，剪切破碎剖面和切削方向不再垂直，引入破碎向量Q，并以{r，s，t}为绝对坐标，重新建立三维力学模型，经过推导可得单元切削刃的切削功率PCut为[17]

PCut=(FS+FT)·V=f(c，φ，hPen，Δh，wb，

γo，λs，V，σp，β，ψc，φre，φdn，φr；rc，η).

(1)

由式(1)可知，在单刃直线切削负载模型中，控制参数为模拟月岩内聚力c、内摩擦角φ、切削深度hPen、切削深度波动量Δh、切削刃刃宽wb、切削刃前角γo、切削刃刃倾角λs、切削速度V、岩石压入硬度σp、剖面切削后角β、密实核与切削方向夹角ψc、切削刃与岩体间当量摩擦角φre、切削刃与密实核间当量摩擦角φdn、密实核与岩体间摩擦角φr，而状态参数为破碎方向角η和岩屑破碎速比rc.根据最小能量耗散准则，当控制参数固定时，一定存在某一组状态参数{rc，η}，使切削功耗PCut最小[18].则切削力FCut和切压力FPen分别为[17]

其中：

FT=FT(cosφre·lβ-sinφre·mβ)，

式中：lβ为后刀面法向单位向量；mβ为后刀面内切削刃法向的单位向量.

2.2 岩石冲击切削破碎负载模型

在受到冲击作用后，模拟月岩将形成3个区域(图5)：OABC为压实破碎区，CDEF为冲击破碎屑，EFG为剪切破碎区.则受力方程可列为

图5冲击切削耦合条件下单元切削刃破碎模拟月岩受力分析Fig.5Force analysis of unit cutting edge crushing simulation moon rock under the coupling condition of impact cutting

式中：FS为作用在切削刃上的合力；Ftx为岩石对破碎区岩屑的合反力在水平方向上的分力；Fty为岩石对破碎区岩屑的合反力在竖直方向上的分力.

FP满足如下关系：

经推导，在冲击切削耦合作用下，单元切削刃破碎模拟月岩所需的切削力和切压力分别为[20]

3 模拟月岩切削负载特性试验

3.1 模拟月岩直线切削特性试验

为了研究切削刃构型参数对切削负载(FCut和FPen)的影响规律，需要在平台上开展直线切削负载试验.由模型(1)可知，切削刃构型参数包括切削刃前角、刃倾角和刃宽，综合考虑钻头的几何构型、切削刃的镶嵌角度以及切削刃的强度，可以确定三者的变动区间分别为-34.75°～23.35°、0°～34.7°、2～5.3 mm.

当切削深度hPen为0.1 mm、切削刃刃宽wb为4 mm、水平切削速度设为26 mm/s时，改变刃倾角，切削力FCut和切压力FPen随前角的变化趋势见图6.

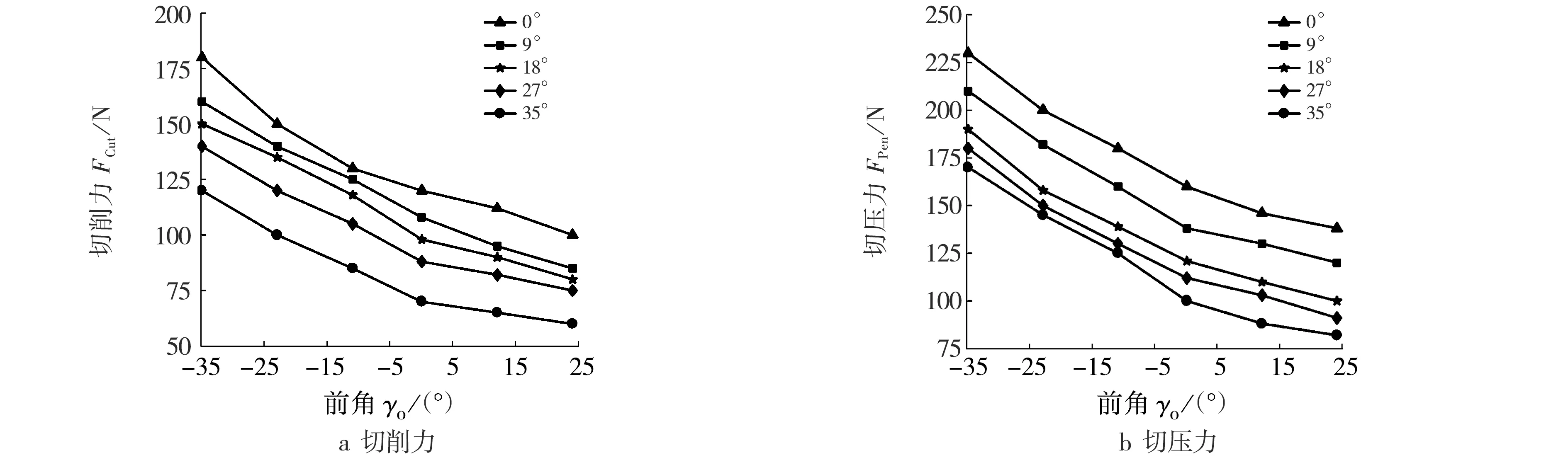
图6切削负载随刃倾角、前角变化Fig.6Variation of cutting load with the side rake angle and the rake

由图6可知：当切削深度和刃宽为固定值时，切削力和切压力均随着前角γo和刃倾角λs的增大而减小.切削负载的下降趋势在前角从-35°增大到0°左右时较为明显，但在前角从0°增大到24°左右时，下降趋势较为平缓.这是因为，当切削深度为固定值时，假设岩石沿着图3所示的破碎面断裂，破碎平面AC(与前刀面垂直)随着前角的增大将顺时针转动，剪切角变大，但是切削深度固定不变，所以会使破碎平面长度变短，切削负载的总体趋势也因此减小，其中，在前角为负的情况下，剪切破碎长度的减小趋势要明显大于正前角的情况.另外，随着刃倾角从0°增加到35°，岩石破碎面AC也开始偏转，且随着刃倾角的增大，岩屑脱离母岩的剪切破碎空间变大，岩屑的剪切破碎角也相应变大，从而使得剪切应力的作用距离变短，切削负载降低.

切削力和切压力随刃宽wb和切削深度hPen的变化趋势见图7.由图7可见：在不同的切削刃参数(前角和刃倾角)下，切削力、切压力随着切削深度、刃宽变大呈线性递增趋势，并且试验值和理论值变化趋势一致.切削刃参数见表4.

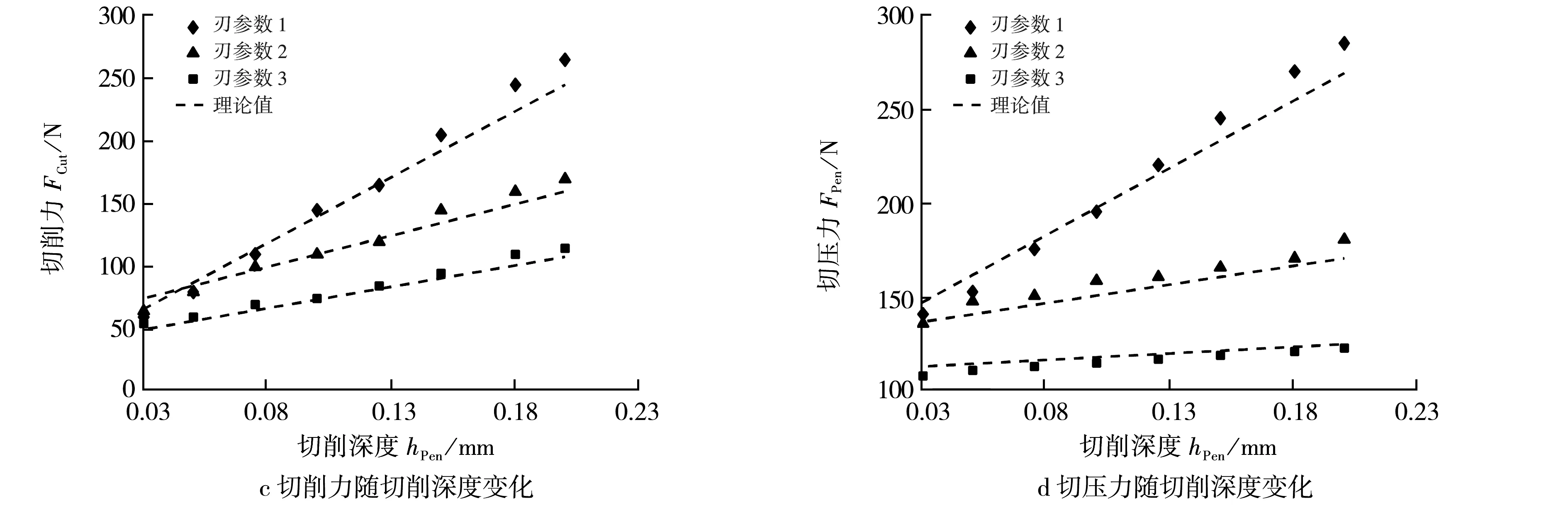
图7切削负载随切削深度、刃宽变化Fig.7Variation of cutting load with the cutting depth and blade width

表4 切削刃参数

3.2 模拟月岩切削冲击破碎负载特性试验

冲击驱动机构的工作原理是圆柱凸轮推动弹簧质量块往复运动提供冲击力.其过程可以分为3个阶段：1)切削冲击耦合阶段.2)力控切削阶段.这个阶段冲击作用时间短，消失后切削刃将受弹簧预紧力作用继续切削岩石，此时弹簧预紧力控制切削深度.3)位控切削阶段.这个阶段冲击锤进入下一个推程运动，弹簧预紧力开始消失，切削刃按照预设切削深度破碎岩石.

为分析切削冲击频率对切削破碎负载的影响规律，在测试平台上开展切削冲击破碎负载特性试验.考虑冲击力传递对切削刃构型参数不敏感，将切削刃参数设定为前角-13°、刃倾角0°、刃宽4 mm，切削速度为26.1 mm/s.在不同切削深度下，分别改变冲击频率，得到模拟月岩切削冲击平均负载，见图8.

图8冲击切削负载随冲击频率、切削深度变化Fig.8Variation of average load of impact cutting with the cut depth and percussion frequency

力控切削阶段模拟月岩切削力和切压力变化趋势见图8 a、b.由图8 a、b可以看出：在不同切削深度下，切削负载均与冲击频率成反比，这是因为在冲击切削耦合下，破碎负载所占比例随着冲击频率的增加而增加，且模拟月岩的剪切破碎长度变小，因此，平均负载逐渐降低.另外，切削负载在切削深度为0.1 mm处分成两个阶段，前一个阶段变化趋势较缓，是因为此时占主导作用的是弹簧预紧力，故只能形成0.1mm左右的切削深度；而在后一个阶段，由于切削深度的增加，破碎负载也急剧上升，进而取代弹簧预紧力占主导作用.

位控切削阶段模拟月岩负载变化趋势见图8 c、d.由图8 c、d可以看出：随着冲击频率的增加，月岩破碎负载在切削深度低于0.1 mm时会增加，在大于0.1 mm后，负载变化趋势不明显.

模拟月岩冲击切削平均负载随冲击频率、切削深度的变化趋势见图8 e、f.由图8 e、f可以看出：随着冲击频率的增加，月岩破碎负载会略有降低，但随着切削深度的增加，破碎负载会明显增加，同时试验值和理论值的变化趋势一致.

4 小 结

本文根据钻头钻进模拟月岩的过程，搭建了单刃直线切削负载特性试验平台，分别开展了岩石直线切削和冲击破碎负载特性试验，结果表明：1)切削刃的切削负载随前角和刃倾角的增加呈减小趋势，且减小趋势在负前角区域较为明显，随刃宽和切削深度的增加基本呈线性递增趋势；2)模拟月岩的切削破碎负载随着冲击频率的增加略有降低，但随着切削深度的增加会显著提高.因此，可以通过增大切削刃前角和刃倾角、提高冲击频率的方式降低模拟月岩的切削负载，这为月岩取心钻具在低作用力下实现高效能钻进作业参数设置提供了一定的参考依据.