半线性椭圆最优控制问题的两网格混合有限元方法

陈红波

(北华大学数学与统计学院，吉林 吉林 132013)

0 引 言

有限元方法广泛应用于偏微分方程支配的最优控制问题中[1-6].国内外学者研究了最优控制问题有限元方法逼近的先验误差估计、超收敛性和后验误差估计，如标准有限元方法[1-2]、混合有限元方法[3-6]，文献[7]系统阐述了最优控制问题的数学理论.

两网格算法是求解非对称、非定和非线性偏微分方程的一种高效离散方法.WU I和ALLEN M B[8]针对半线性反应扩散方程提出两网格扩张混合有限元算法；DAWSON C N等[9]应用两网格有限差分方法求解非线性抛物方程；BI C和GINTING V[10]给出两网格有限体积方法来求解线性和非线性椭圆方程，此外，他们还研究了拟线性椭圆问题[11].据我们所知，LIU H和WANG S[2]首次将两网格算法应用到最优控制问题；HOU T和LENG H[6]讨论了Stokes方程最优控制问题的伪应力-速度混合有限元方法的超收敛性并给出了两网格格式.

本文考虑下面的半线性椭圆最优控制问题

(1)

divp+φ(y)=f+u，p=-A(x)grady，x∈Ω，

(2)

y=0，x∈∂Ω，

(3)

.

(4)

假设对任意的R>0都有函数φ(·)∈W2，∞(-R，R)∩H3(-R，R)，对任意的y∈H1(Ω)满足φ′(y)∈L2(Ω)且φ′>0.系数矩阵A(x)=(aij(x))是一个对称的矩阵函数，其中aij(x)∈W1，∞(Ω)，并满足

1 最优控制问题的混合有限元方法

令V=H(div；Ω)={v∈(L2(Ω))2，divv∈L2(Ω)}，W=L2(Ω).问题(1)～(3)的弱形式为：找到(p，y，u)∈V×W×Uad，使得

(5)

(A-1p，v)-(y，divv)=0， ∀v∈V，

(6)

(divp，w)+(φ(y)，w)=(f+u，w)， ∀w∈W，

(7)

这里(·，·)表示L2(Ω)空间中的内积.

由文献[7]可知问题(5)～(7)有局部唯一解(p，y，u)，同时存在对偶状态(q，z)∈V×W使得(p，y，q，z，u)满足如下的最优性条件：

(A-1p，v)-(y，divv)=0， ∀v∈V，

(8)

(divp，w)+(φ(y)，w)=(f+u，w)， ∀w∈W，

(9)

(A-1q，v)-(z，divv)=-(p-pd，v)， ∀v∈V，

(10)

(divq，w)+(φ′(y)z，w)=(y-yd，w)， ∀w∈W，

(11)

(12)

由文献[5]可知，控制变量的表达式为

(13)

假设f、yd∈L2(Ω)，pd∈(H1(Ω))2，我们有u∈L∞(Ω).

令Th表示区域Ω上的拟一致三角剖分，hT表示单元T的直径且记h=maxhT.令Vh×Wh⊂V×W表示最低阶的Raviart-Thomas混合有限元空间(见文献[12])，定义为

这里Pm(T)表示单元T上次数不超过m的多项式集合，x=(x1，x2)表示一个向量，

给出混合有限元格式之前，我们先介绍两个算子.

定义标准的L2(Ω)正交投影Ph：W→Wh，对任意的φ∈W都满足

(Phφ-φ，Wh)=0， ∀wh∈Wh，

(14)

.

(15)

Fortin投影[12]Πh：V→Vh，对任意的q∈V都满足

(div(Πhq-q)，wh)=0， ∀wh∈Wh，

(16)

(17)

.

(18)

于是问题(5)～(7)的混合有限元离散格式如下：找到(ph，yh，uh)∈Vh×Wh×Uh使得

(19)

(A-1ph，vh)-(yh，divvh)=0， ∀vh∈Vh，

(20)

(divph，wh)+(φ(yh)，wh)=(f+uh，wh)， ∀wh∈Wh

.

(21)

类似地，如果(ph，yh，uh)为问题(19)～(21)的一个解，则存在离散对偶状态(qh，zh)∈Vh×Wh使得(ph，yh，qh，zh，uh)满足下面最优性条件：

(A-1ph，vh)-(yh，divvh)=0， ∀vh∈Vh，

(22)

(divph，wh)+(φ(yh)，wh)=(f+uh，wh)， ∀wh∈Wh，

(23)

(A-1qh，vh)-(zh，divvh)=-(ph-pd，vh)， ∀vh∈Vh，

(24)

(divqh，wh)+(φ′(yh)zh，wh)=(yh-yd，wh)， ∀wh∈Wh，

(25)

(26)

本文中，真解和数值解可以表示为

(p，y，q，z)=(p(u)，y(u)，q(u)，z(u))，

(ph，yh，qh，zh)=(ph(uh)，yh(uh)，qh(uh)，zh(Uh)).

下面，给出一个重要结果(文献[5]).

引理1令(p，y，q，z，u)∈(V×W)2×Uad和(ph，yh，qh，zh，uh)∈(Vh×Wh)2×Uh分别表示问题(8)～(12)和(22)～(26)的解.假设p、q∈(H2(Ω))2和u∈W1，∞(Ω)∩H2(Ω)，于是有

(27)

(28)

这里Gh表示修复算子，具体定义可见文献[1].

2 最优控制问题的两网格算法离散

两步两网格算法：

步1.找到(pH，yH，qH，zH，uH)∈(VH×WH)2×Uh满足

(A-1pH，vH)-(yH，divvH)=0， ∀vH∈VH，

(29)

(divpH，wH)+(φ(yH)，wH)=(f+uH，wH)， ∀wH∈WH

.

(30)

(A-1qH，vH)-(zH，divvH)=-(pH-pd，vH)， ∀vH∈VH，

(31)

(divqH，wH)+(φ′(yH)zH，wH)=(yH-yd，wH)， ∀wH∈WH，

(32)

(33)

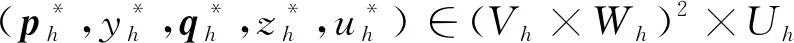
(34)

(35)

(36)

(37)

(38)

下面分析收敛性.

.

(39)

证明：由式(8)～(11)和式(34)～(37)，可得误差方程

(40)

(41)

(42)

(43)

将函数φ(y)在yh处泰勒展开得

(44)

结合式(14)、(16)和(44)，将式(40)～(43)整理为

其中

φ1(vh)=-(A-1(p-Πhp)，vh)，

因为φ1(vh)、φ2(vh)、ψ1(wh)和ψ2(wh)可以看作分别是定义在空间Vh和Wh上关于vh和wh的线性泛函，由文献[13]中的稳定性结果可知

(45)

.

(46)

利用逆估计、式(27)～(28)和式(15)，可推出

(47)

这里PH的定义与Ph类似.

根据Cauchy不等式、式(17)和关于矩阵A的假设，可知

(48)

.

(49)

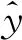
(50)

结合式(50)、Cauchy不等式、式(15)和函数φ的假设，可证

(51)

.

(52)

将式(48)～(49)和(51)～(52)代入到式(45)～(46)中并结合式(15)、(17)～(18)、(28)、(47)和三角不等式，即可完成定理证明.证毕.

.

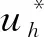
(53)

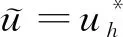
(54)

利用式(54)、(13)～(14)和Young’s不等式得

(55)

结合式(55)和(39)，可证式(53)成立.证毕.