半线性双曲积分微分方程的一个线性有限元格式及其收敛性分析

王 凯，徐长玲

(北华大学数学与统计学院，吉林 吉林 132013)

0 引 言

本文考虑下面的半线性双曲积分微分问题：

(1)

y(X，t)=0，X∈∂Ω，t∈J，

(2)

y(X，0)=y0(X)，X∈Ω，

(3)

yt(X，0)=y1(X)，X∈Ω，

(4)

a1rTr≤rTAr≤a2rTr

.

(5)

另外，假设B(t，s)=B(x，t，s)也是一个2×2阶矩阵，且存在正数M1和M2使得

(6)

.

(7)

双曲积分微分方程的初边值问题(1)～(4)出现在具有记忆性质材料的热传导、核反应堆中热交换等实际问题中，这类问题的研究在理论和应用方面均有一定的实际意义.有限元方法作为一种重要的数值方法，已经成功应用于求解这类问题.国内外学者针对问题(1)～(4)及其衍生模型问题的有限元逼近取得了很多先验误差估计和超收敛方面的结果[1-7].例如，文献[1]考虑了抛物和双曲积分微分方程有限元方法的先验误差估计；文献[2]给出了一类非线性双曲积分微分方程的全离散Crank-Nicolson有限元格式；文献[3]考虑了一类非线性双曲积分微分方程的半离散有限元逼近及误差分析；文献[4]研究了抛物和双曲积分微分方程有限元方法的超收敛性；文献[5]考虑了伪双曲积分微分方程的双线性元逼近并给出高精度分析.随着有限元方法的发展，非协调有限元方法也逐渐应用于求解双曲积分微分方程[6-7].

近几年，为了有效求解半线性问题(1)～(4)和强非线性双曲积分微分方程初边值问题，一些专家学者发展了两网格有限元方法.例如，文献[8]针对半线性问题(1)～(4)的向后欧拉有限元逼近设计了两网格算法；文献[9]构造了一类非线性双曲积分微分方程的全离散两网格有限元格式并给出最优误差估计.

受文献[8-9]中两网格格式细网格上的线性化思想启发，本文针对半线性问题(1)～(4)构造一个新的二阶线性有限元逼近格式并分析收敛性.

1 线性有限元逼近

(8)

这里(·，·)表示L2(Ω)空间中的内积.

变分问题(8)的解的存在性和唯一性参见文献[1-2].

这里Pm(κ)表示单元κ上总次数不超过m的多项式集合.

下面，引入Ritz-Volterra投影算子[11]Rh：V→Vh，满足：对任意y∈V，

.

(9)

同时，有下面的逼近性成立

.

(10)

(11)

(12)

(13)

这里ytt(X，0)=div(A▽y0(X))+f(y0(X)).

2 误差估计

利用Ritz-Volterra投影和对时间的离散导数转移技巧，可以推出下面的收敛性结果.

(14)

在式(14)中取vh=dtξn+1+dtξn，同时将两边乘以τ并对n从1到l求和，可推出

(15)

下面，分别估计K1～K7.对于K1，利用ξ0=0、式(6)、Cauchy-Schwarz不等式和Young’s不等式，可得

(16)

这里

类似于K1的估计，可证

(17)

(18)

.

(19)

利用Cauchy中值定理、Cauchy-Schwarz不等式、Young’s不等式和式(10)，可将K5估计为

(20)

对于K6，利用Cauchy中值定理、Cauchy-Schwarz不等式和Young’s不等式，易证

.

(21)

下面估计K7.由泰勒展开式

和Cauchy中值定理，可知

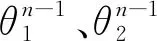
因此，利用Cauchy-Schwarz不等式、Young’s不等式、式(10)、式(7)和Poincaré不等式，可将K7估计为

.

(22)

将式(16)～(22)代入式(15)并利用式(5)和ξ0=0，可得

(23)

.

(24)

对于充分小的τ，将式(24)代入式(23)并应用离散的Gronwall’s不等式可推出

.

(25)

最后，利用式(24)～(25)、式 (10)、Poincaré不等式和三角不等式，即可完成定理证明.证毕.

注1定理1针对新的线性有限元格式(11)～(13)给出了详细的收敛性分析.本文的方法和定理1的证明技巧可以进一步推广到强非线性双曲积分微分方程的初边值问题中.