核心素养下小学数学渗透模型思想策略探究

陈　灵

核心素养下小学数学渗透模型思想策略探究

陈灵

（福建省泉州市鲤城区实验小学，福建泉州362000）

数学核心素养包括数学建模、数学运算、直观想象以及数据分析等内容，其中数学建模乃是核心素养的主要内容之一，是小学数学教学非常重要的任务，也是提高学生分析问题能力、解决问题能力，培养学生数学知识应用意识的重要内容。在新课改要求下，广大数学教师当重视学生建模能力培养。本文以小学数学教学为例，聚焦数学核心素养要求，探讨如何在小学数学中培养学生模型思想。

小学教育；数学教学；核心素养；模型思想

《义务教育数学课程标准》（2011年版）对模型思想进行了详细论述，强调模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。数学模型思想是学生在感知数学模型、建立数学模型、应用数学模型的过程中逐步形成的一种思维模式，是学生思维发展的直接体现，是需要学生在数学学习过程中观察、感知、探索、总结、归纳和应用的。在小学数学教学中融合数学模型思想旨在促进学生抽象思维发展，为提升学生数学核心素养奠定基础。基于此，数学教师也应当充分结合小学生认知水平、理解能力、思维发展规律以及小学数学教材大纲要求，创造性地将数学模型思想融合到数学教学过程中，以数学教学促进学生思维能力发展。

一、小学数学教学中加强学生模型思想培养的意义

（一）促进学生数学思维发展

数学思想融合到小学数学教学中的重要步骤是引导学生建立数学模型，而建模这一过程其实就是学生将抽象数学概念与实际问题建立联系并互相转化的过程，需要学生充分结合已有认知经验，合理应用数学变量、数学公式、数学概念。整个过程帮助学生实现了知识内化和吸收，让学生对数学知识的理解更透彻，逻辑思维和应用能力得到充分发展。因此，从这一角度而言，数学模型思想融合到小学数学教学中是有助于学生数学思维发展的。

（二）提高学生解决问题的能力

模型思想的本质在于将数学问题简化，其最终目的指向“问题解决”。将模型思想融合到小学数学教学之中也是为了引导学生建立数学模型，应用数学模型解决实际问题。当学生具有一定建模能力之后，自然能够将看似复杂的数学问题简单化，灵活机智地运用所学数学知识解决实际问题，从而提高自身解决问题的效率。

（三）增强学生运用知识的意识

学以致用是学习的最终落脚点，培养学生应用意识也是数学新课标以及数学核心素养对广大教师提出的根本要求。将数学模型思想融合到小学数学教学之中无疑是迎合了新课标和核心素养发展趋势，有利于引导学生将生活实际问题与数学知识高度关联。比如《图形与几何》教学中，教师引导学生将拱形原理与“赵州桥”联系；学习多种几何图形时，可引导学生联系楼盘开放商建立的“沙盘模型”……通过关联生活的教学让学生发现数学知识在生活中的实际应用，也促使学生主动到生活中探寻数学的“影子”，唤起学生主动学习和应用数学知识的意识。

二、基于模型思想的小学数学教学策略

（一）立足于数学教材，引导学生认识数学模型

培养学生数学建模能力的前提是学生对模型有初步了解，认识多种数学模型。所以，在小学数学教学中，数学教师首先应引导学生体验数学模型思想，思索和分析各种不同类型的数学模型，为学生主动搭建和应用数学模型打下坚实基础。结合笔者对小学生认知水平、理解能力、思维发展现状的了解来看，当前小学数学教学中可重点引导学生认识如下几种数学模型：

一是公式模型。数学教材中所有公式的本质都是一种数学模型，比如，路程=时间×速度；总价=单价×数量；矩形的面积=长×宽，长方体的体积=长×宽×高=底面积×高……可以说公式模型是最基础和简单的模型，也是学生可以直接运用的一种数学模型。这种模型能够帮助学生快速解决实际问题，提高学生解决问题的效率。在小学数学新知教学中，数学教师当有意识地渗透公式模型思想，引导学生认识多种公式模型。

二是方程模型。方程模型在小学高年级数学教材中体现较多，其本质是学生结合实际问题列出方程，并解决实际问题。方程模型中引出了未知数，能够帮助学生顺向推导和分析问题，快速找到隐藏在数学问题中的未知量和已知量的数学关系，从而搭建出完整的数学模型。这种数学模型广泛应用于应用问题中，搭建和应用这种模型有助于培养学生数学阅读能力、信息收集与整合能力、数据分析与处理能力。

三是几何模型。几何模型是用几何概念描述数学物体形状的一种模型，是小学数学教材中广泛应用的一种模型。几何模型的建立过程是运用数学概念、定理、公式将实际问题抽象成简单几何图形的过程，充分体现了数形结合思想，也有利于学生对数学抽象、概括思维发展。

（二）重视过程教学，引导学生开展数学建模活动

让学生经历建模过程是培养学生模型思想必不可少的环节。数学新课标明确强调了学生自主体验的重要性，要求广大教师重视“过程教学”，尽可能给学生提供一个发现、探索、总结知识的过程，让学生在亲历中发现规律，总结结论，解决问题。因此，数学教师应重视教学过程，引导学生开展数学建模活动。具体如何操作呢？数学新课标也给教师们指明了方向：“问题情境——建立模型——求解验证”，借助这三大环节开展建模探究活动，让学生能够对数学模型有更深层次理解。当然，在这一过程中，数学教师也应该扮演好学生的引导者、帮助者角色，注意提醒和点拨学生，引导学生自主思考、合作探究、交流分享，让学生真正在过程中实现思维碰撞，在过程中发现规律，在过程中解决问题，在过程中获得模型思想的本质感悟。文章以小学六年级下册《自行车里的数学》这一内容为例，进行了如下尝试：

环节一：问题情境

教师谈话导入情境：我国是一个自行车大国，每天来回穿梭在街头的自行车不计其数，同学们有没有发现自行车里也有很多数学知识呢？你从自行车里了解到了哪些数学知识？鼓励学生结合自身日常观察，说一说自行车相关知识。比如，启发学生从自行车的种类（普通自行车、变速自行车、山地自行车等）角度谈论；也可以鼓励学生将自信车的前后轮与“圆”这一知识建立联系，引导学生按照车轮直径分类；还可以启发学生按照使用对象分类：男车、女车、童车。待激活学生学习热情后，教师进一步设置问题：自行车是怎样前行的呢？鼓励学生联系个人生活经验以及所学数学知识，小组内互相说一说，然后总结结论。为进一步激活学生数学思维，教师继续追问：蹬一圈车轮就转一圈，走的路即是车后轮的一周周长，你认为对吗？前齿轮转一圈，后齿轮转多少圈呢？引导学生合作完成下表（表1）。

表1

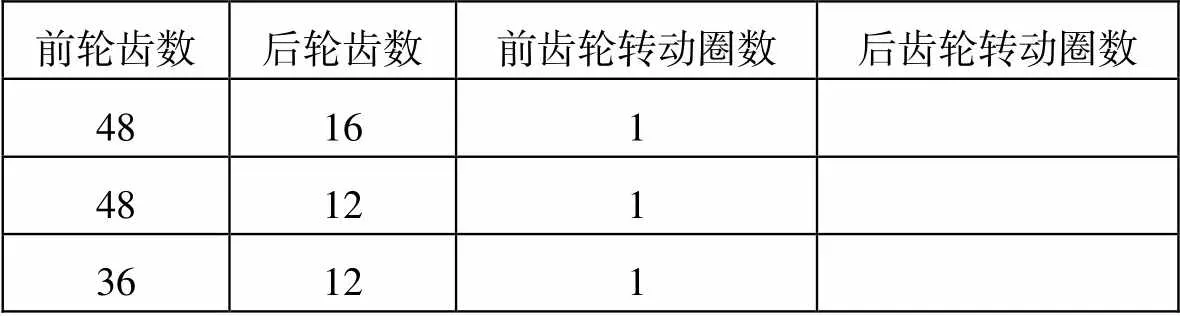
前轮齿数后轮齿数前齿轮转动圈数后齿轮转动圈数 48161 48121 36121

环节二：建立模型

建立模型是最关键的一步。在引导学生探究数学模型的过程中，数学教师应走出传统“灌输式”教学模式的束缚，避免直接告诉学生数学规律、数学答案。相反，教师更应该引导学生主动探索数学规律，建立数学模型。所以，在学生针对上述问题情境有进一步探究之后，数学教师要有意识地引导学生将实际问题与数学知识建立直接联系。

首先教师追问学生：从上述表格数据可以发现什么？启发学生将实际问题转化为已经学习过的数学知识，引导学生将实际问题转化为“圆”“比例”“排列组合”等数学知识，建立如下数学模型：

其次教师提出新的问题：蹬一圈，自行车能走多远？请学生谈一谈自己解决这一问题的方法和发现。

借助已有知识经验，学生很容易找到解决问题的方法：测量（差距较大）和计算。

在这一环节中，教师充分尊重学生的主体地位，将探索知识的主动弃教给学生，让学生主动从数学的角度分析生活问题，建立数学模型，让学生真正发现“蹬同样多的圈数，自行车走的距离与车轮（半）直径、前后齿轮齿数的比值有关”。

环节三：求解验证

建立数学模型之后，最重要的一步就是引导学生利用数学思想、数学知识、数学模型解决实际问题，帮助学生逐步形成一套完整的解题思路。这是培养学生数学建模素养的本质。因此，广大数学教师在引导学生初步建立数学模型后，就需要教给学生利用模型解题的方法，其中数形结合思想乃是笔者在教学过程中最常采用的方法之一，也是利用模型解决问题最重要的方法之一。因此，为了进一步加深学生对数学模型的理解，在学生完成上述探究活动之后，还可以增设“探究变速自行车中的数学问题”活动，出示如下记录单（表2）。

求解问题一：一个变速自行车有两个前齿轮和6个后齿轮，能变化出多少种速度？从表中数据可以发现有两个比的比值相等，所以6×2－1＝11（种）速度。

表2

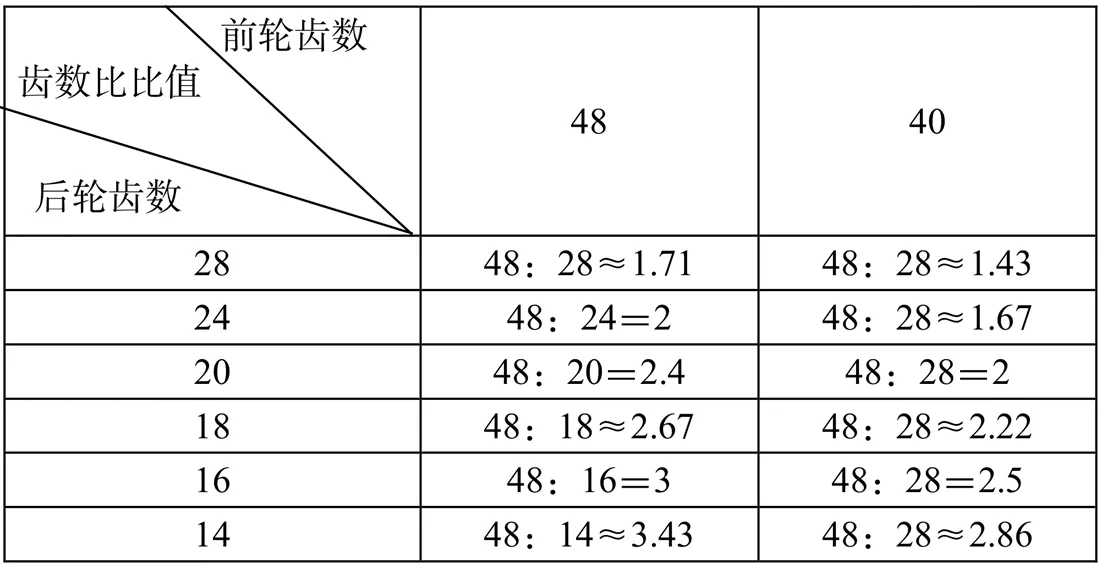
求解问题二：蹬同样的圈数，哪种组合使自行车走得最远？

教师先让学生分析上述表单数据，然后鼓励学生合作交流，最后师生共同总结结论：①前后齿轮齿数相差(比值)越大，后轮的转动圈数就越多；②前、后齿轮齿数相差(比值)大的，比值就大，这种组合走得就远；③前、后齿轮齿数相差(比值)少时，车速较慢。引导学生自己建立模型的基础上，进一步解释和验证规律将变速自行车里的数学问题转化为“比例”知识。

整个教学过程推进了数学模型的建立，让学生在学习过程中了解了数学知识与生活的广泛联系，引导学生主动建立了普通自行车的速度与其内在结构关系的数学模型，帮助学生在“过程学习”中获得了运用数学知识解决实际问题的思考方法——建立数学模型，也进一步加深了学生对所学知识的理解。

（三）加强拓展运用，提升学生建模素养

培养学生建模素养有利于提高学生数学知识应用能力。而从“教”之角度而言，数学建模其实是一种教学手段，但从学生“学”的角度而言，数学建模就是一种能力，一种学习策略，一种解决问题的技巧和方法。故此，要想通过数学教学培养学生建模素养，提高学生数学知识应用能力，数学教师还需要在教会学生建立模型和以模型解决问题之后，引导学生反复利用模型，并且将模型进行归纳整理，从而达到举一反三、迁移运用的教学目的。同样以《自行车里的数学》这一内容为例，在课堂接近尾声时，不妨给学生来一个拓展延伸，设置如下当堂练习题：

习题1：一辆自行车的前齿轮齿数是32，后齿轮数是16，前后车轮的直径为66cm，①请你算一算蹬一圈，自行车行驶多远？②小明家和学校的距离大约有500米，如果蹬自行车上学，他要蹬多少圈？

习题2：一辆变速自行车的前齿轮数是2，分别有46和38个齿，后齿轮数是4，分别有20、16、14、12个齿，车轮的直径66cm。自行车运动员在赛车时会经历顺风和爬坡两种路段，请你为运动员在不同的路况下选择前后齿轮。

联系当堂教学内容设计习题，既可以帮助学生实现“堂堂清”，也能够进一步引导学生运用数学模型解决实际问题，进一步促进学生数学模型思想发展，逐步提升学生数学建模素养。

三、结束语

综上所述，学习知识的最终目的是运用知识解决问题，而解决大部分数学相关问题都涉及不同数学模型。广大数学教师当重视学生建模能力培养，在课堂教学中充分给予学生探究活动空间，密切联系学生实际生活，引导学生运用已有知识和生活经验开展观察、操作、推理等活动，让学生真正感知数学模型，主动建立数学模型，应用数学模型，提高学生解决问题能力，促进学生核心素养发展。

[1] 李建卿.核心素养背景下初中数学渗透模型思想的策略[J].数学大世界(上旬),2019(08).

[2] 严苏娟.以数学建模思想培养学生数学核心素养的教学实践[J].考试周刊,2018(11).

[3] 沈国酰.将数学建模思想落到实处——以“解决问题的策略”为例[J].数学教学通讯,2017(01).

[4] 郭守贵.数学建模思想在小学数学教学中的应用分析[J].青海教育,2017(01).

[5] 王明会.在小学数学教学中融入数学建模思想的策略研究[J].天天爱科学(教育前沿),2021(05).

G622

A

1002-7661(2022)14-0150-03

本文系福建省科学“十三五”规划2020年度课题《在小学数学教学中渗透模型思想的研究》课题成果，课题编号FJJKXB20-1045。