分形与压缩感知理论相结合的图像编码算法研究

李高平

(西南民族大学数学学院，四川成都 610041)

图像作为蕴涵信息量最大的媒体，它占有的海量数据量给图像数据的储存与传输带来极大困难，成为图像技术应用的瓶颈.如何高效、实时地压缩图像，以较少的空间储存大量图像是解决数据有效储存与传输的关键问题，是信息化社会所依赖的主要技术基础之一.

分形图像编码作为一种全新的图像编码方法，对信源的先验知识要求极少，更多地利用图像的自相似性及比例特性.它虽然具有压缩原理新颖、高压缩比、解码效果好、抗干扰能力强等优点，但它与主流采用的编码方法相比还没有明显优势，是一种编码过程特别耗时而其解码过程快的不对称编码技术.目前很多研究工作都是以 Jacquin 提出的分形块编码为基础[1]，在基本理论、编码方案改进、应用扩展等方面进行探索[2-9].

压缩感知是将压缩和采样两个过程一并进行的，若信号在某一个正交空间具有稀疏性，就能在原始信号投影到更低维信号空间时，以远低于奈奎斯特采样频率来采样该信号，并可能以高概率重建该信号，但它存在图像尺寸太大时，因计算量大而实时性差的问题.压缩感知的关键要素包括稀疏表示方法[10-11]、测量矩阵的选择[12-14]和重构算法的设计[15-17].

尽管分形图像编码、图像压缩感等新一代编码技术有各自公认的显著优点，但纯粹基于分形理论的编码方法存在编码时间长、实时性差的问题.同样，纯粹基于图像压缩感知理论的编码方法存在图像重建时耗时很长，与目前广泛使用的编码方法相比，还缺乏竞争力，离完全实用还有相当距离.因此，本文将分形图像编码与图像压缩感知两种编码方法结合起来，扬二者之长，避二者之短(即分形法是编码过程长、解码过程快，压缩感知恰好相反)，研究性能更优的混合编码算法，以全搜索分形图像编码算法为基本框架，融入压缩感知图像编码算法中的观测矩阵.首先将原始图像分成大小相等的图像子块，对每个图像子块采用高斯随机矩阵来采样它的观测值，然后求出其均值与标准差，据此定义每个子块的均标积特征值，最后在编码阶段的值域R 块与码书D 块的匹配过程中，以该特征值为依据设置剔除条件，搜索最佳匹配D 块的范围远小于全局搜索范围. 实验结果表明，本文提出的混合编码算法与全搜索分形算法、压缩感知编码算法相比，以PSNR 度量的重建图像质量分别降低约0.8 dB、2.58 dB 的情况下，编码时间平均分别减少了90 %、80 %以上，其主观质量评价指标SSIM 值几乎无变化.

1 分形与压缩感知结合的图像编码算法

1.1 基本分形图像编码流程图

基本分形图像编码[1]过程流程图如图1 所示.

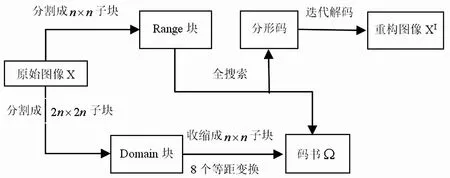
图1 基本分形图像编码过程流程图Fig.1 The basic fractal image coding process flow chart

1.2 压缩感知图像编码流程图

压缩感知图像编码方法流程图如图2 所示.

图2 压缩感知图像编码流程图Fig.2 The flow chart of compressive sensing image encoding

1.3 分形与压缩感知相结合的图像编码算法流程图

将分形与压缩感知相结合的图像编码算法流程图如图3 所示.

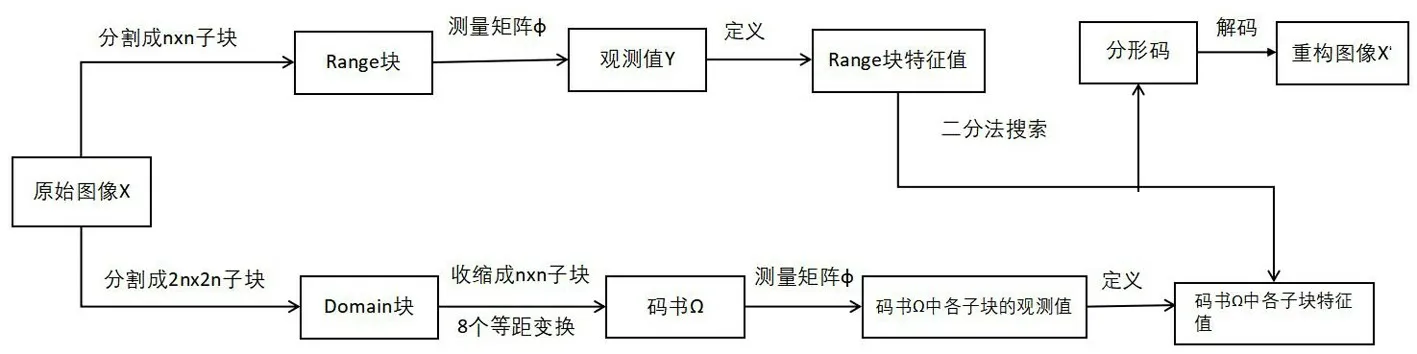
图3 分形与压缩感知结合的图像编码算法流程图Fig.3 The flow chart of image coding algorithm combining fractal andcompressive sensing

具体步骤为:

Step1:将原始图像分割成n×n大小的待编码Range 块，以及 2n×2n大小的 domain 块(收缩成n×n大小后，用作码书Ω 中的子块)；

Step2:用设计的观测矩阵采样待编码Range 块与码书Ω 中每个子块的测量值；

Step3:根据测量值定义待编码Range 块与码书Ω中每个子块的均标积特征值，并将码书Ω 中的子块按其特征值进行升序排列；

Step4:对每个待编码Range 块，用二分法在码书Ω 中找到与其均标积特征值最接近的子块，按照剔除条件寻找其最佳匹配块，并记录它的分形码；

Step5:按照Step4 找出的所有待编码Range 块的分形码的集合，就构成了原始图像的分形码. 重建图像时，就用该分形码按照分形编码的解码迭代算法来生成.

1.4 算法的理论基础

本文中测量矩阵Ф 选取的是高斯随机矩阵，在依据子块测量值定义子块的特征值时，既要消除对比度因子的影响，又要满足特征提取简单可行，且具有代表性.否则，在邻域内找到的局部匹配块就不是全局匹配块，导致用局部匹配块代替全局最优匹配块的数量太多，造成解码图像质量下降很大.

式中μ(Y)为图像子块X的测量值Y的均值，σ(Y)为图像子块X的测量值Y的标准差.

在自仿射变换下，讨论R 块与码书中D 块的均标积特征满足什么条件，才有可能成为最优匹配块对.找寻每个待编码R 块的最优匹配块时，通过遍历码书Ω 来得到自仿射变换w下均方根误差最小的D块作为最优匹配块.鉴于均标积特征在自仿射变换w下具有不变性，所以，应有下式成立:

从上式可以看出，D 块能成为R 块的最佳匹配块，在均标积特征意义下，也应该是近邻.

1.5 快速编码算法方案

图像分割出的待编码R 块数量、码书Ω 容量以及搜索最佳匹配块的方式这三个关键因素是设计快速编码过程方案时需要重点考虑的.前面2 个因素由分割图像方案决定，在此只讨论何种搜索方式才能在码书Ω 中快速找到待编码R 块的最佳匹配D 块，依据上式(2)可知，R 块和D 块能组成匹配对，要求D块的T(D)值应该与R 块的T(R)值接近，也就是说在均标积特征意义下，R 块的最优匹配Dm块应位于那些D 块均标积特征值与R 块均标积特征值比较接近的D 块子集中.所以，在设计搜索方案时，首先按照码书Ω 中的全体D 块的均标积特征值进行升序排列，即T(Di)≤T(Di＋1)，然后，在升序码书 Ω 中采用二分法搜索与编码R 块均标积特征值T(R)相差最小的初始匹配块D 块:

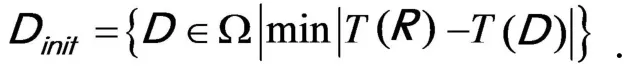
如果记R 块与初始匹配块Dinit间的误差Einit为

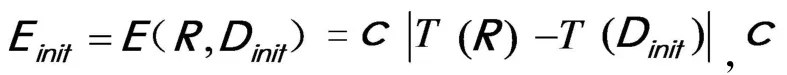
为常数.

按照上述建立的剔除条件，在码书Ω 中搜寻与R块匹配误差满足式(3)所对应的D 块后，记录其位置序号m、自仿射变换中的量化参数及等距变换的序号t，它们就构成该R 块的分形码. 待编码图像的所有R 块的分形码集合就构成了该幅图像的分形码.

2 仿真实验结果

实验的测试对象为4 幅复杂性各异的图像Lena、Boat、Peppers 和 polar bear(512 × 512，8bit 量化)，采用固定方块分割图像，R 块、D 块大小分别为8 ×8、16 ×16，码书步长为 8. 此时，待编码 R 块总数量为4 096，码书Ω 的容量为3 969，采样率p=0.5，仿真实验平台为PC 机 (Intel(R) Core(TM) i5-8500 CPU ＠3.00 GHz 3.00 GHz).

2.1 均标积特征的有效性验证

本文依据图像子块测量值定义的均标积特征，是否刻画了图像子块中的自相似性，下面通过仿真实验测出编码R 块在全搜索中得到的最优匹配D 块，与在均标积特征意义下按照剔除条件得到的匹配D 块，其距离表明了均标积特征的有效性.

表1 中数据表明，4 幅测试图像在均标积特征意义下所做的邻域搜索得到的匹配块的位置与全搜索中得到的最优匹配块所在位置完全一样的比例平均为8.5 %、相距10 的比例平均为17.6 %、相距50 的比例平均为87.2 %.这说明在均标积特征意义下，大多数的待编码R 块的最优匹配块就在较小邻域半径的邻域内，验证了它的有效性.

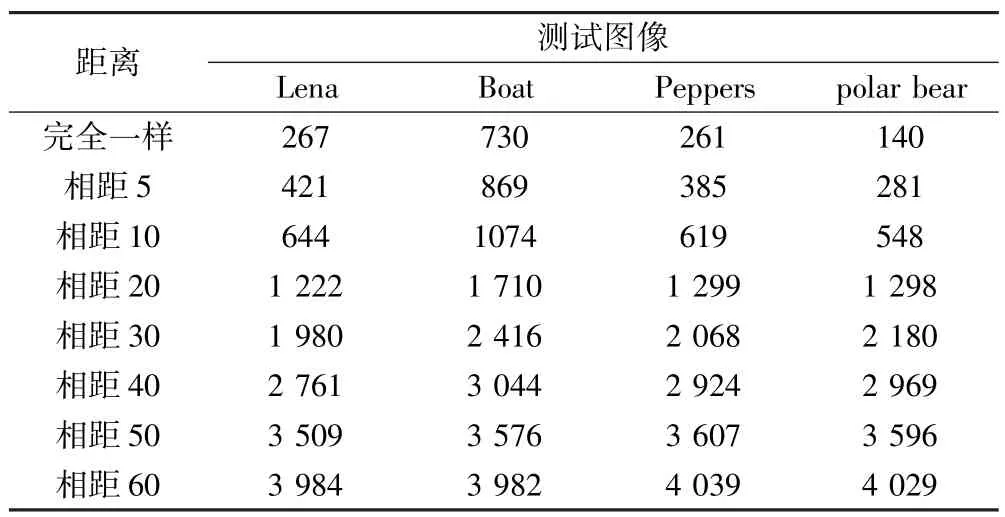
表1 邻域搜索得到的匹配块距离最优匹配块的距离统计Table 1 The distance statistics of the optimal matching block vs.the matching block by neighborhood search

2.2 混合编码算法的有效性验证

为了验证分形与压缩感知相结合的图像混合编码算法的有效性，选编码时间(秒)、峰值信噪比PSNR(dB)和结构相似性SSIM(structural similarity)为测试性能参数来做仿真对比实验.本文算法(p=0.5，观测矩阵采用高斯随机矩阵)与基本分形编码算法的对比实验结果见表2.

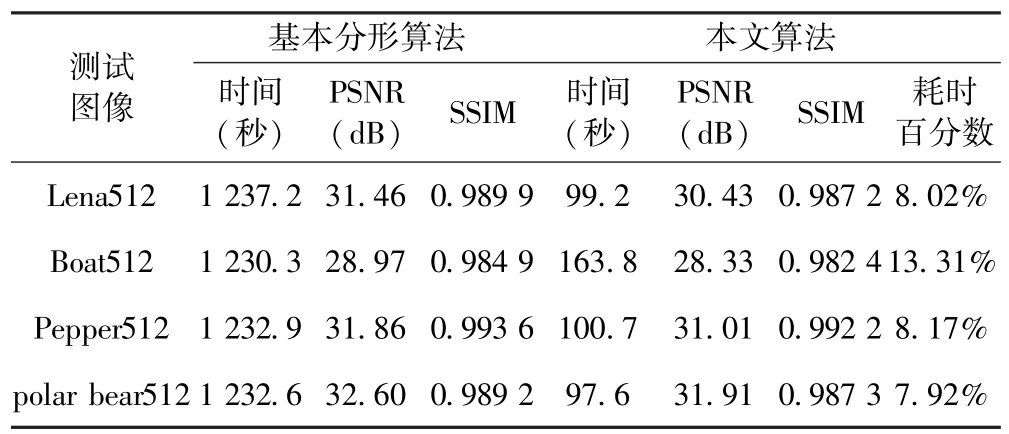
表2 本文算法与基本分形算法对比结果Table 2 The comparison between the proposed algorithm and the basic fractal algorithm

从表2 数据可知，本文所提混合算法加快编码过程的速度是相当明显的，若降低重建图像质量约0.8 dB，则编码过程平均耗时仅为基本分形算法所需时间的9.36 %左右.若考虑到人眼的视觉特性，采用衡量两幅图像相似度的SSIM 指标来评价图像感知质量，该指标值仅平均下降约0.002 1，表明本文算法的重建图像的主观质量几乎无变化，但编码时间比基本分形算法平均减少了90 %以上.

本文算法与压缩感知图像编码算法(图像分块大小为16 ×16，p=0.5，稀疏矩阵采用离散余弦变换矩阵，观测矩阵采用高斯随机矩阵，重构算法采用正交匹配追踪算法)的对比实验结果列于表3.

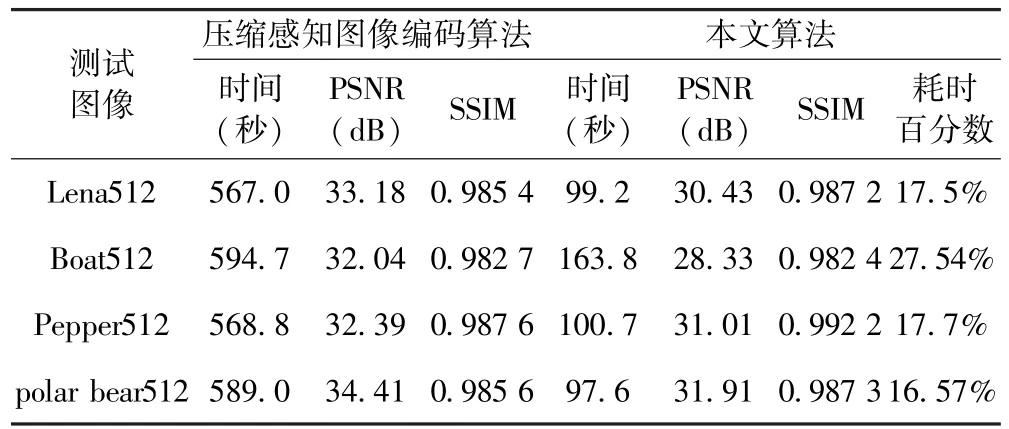
表3 本文算法与压缩感知图像编码算法对比结果Table 3 The comparison between the proposed algorithm and the compressive sensing image encoding algorithm

同样从表3 数据可以看出，对所给4 幅测试对象，本文所提算法与压缩感知图像编码算法从时间指标上看，提速效果也是相当明显的，在重建图像质量降低约2.58 dB 的情况下，编码过程耗时仅为全搜索算法所需时间的19.83 %左右，且它们的主观质量指标SSIM 值平均增加约0.002. 这充分说明本文所提混合编码算法的重建图像在主观质量不降低的情况下，编码时间平均减少了80 %以上.

仿真实验所用的4 幅测试图像在基本分形算法、压缩感知图像编码算法与本文所提出的分形与传感压缩相结合的图像混合编码算法的重建图像分列于 下图4，从主观质量上看几乎无差别.

图4 三种图像编码算法的重建图像对比Fig.4 Thereconstruction image comparison of three image coding algorithms

3 结论

把压缩感知理论中的测量矩阵引入到分形图像编码算法中，提取图像子块的有效信息，去除冗余信息还是有效的.在编码过程中，依据图像子块测量值定义的均标积特征来设置剔除条件，把与R 块不太可能组成匹配对的D 块排除，就把消费时间最多的R块与码书Ω 中D 块的匹配全搜索过程转化为邻域搜索过程，搜索范围大大降低，节约了编码时间.通过4幅测试图像的仿真实验数据，验证了大多数的待编码R 块的最优匹配D 块位于较小邻域半径的邻域内，表明了编码过程的全搜索被邻域搜索取代是可行的.本文据此所提混合分形编码算法与基本分形算法、压缩感知图像编码算法相比，在主观质量评价指标SSIM值几乎没有变化、以PSNR 度量的重建图像质量分别降低约0.8 dB、2.58 dB 的情况下，所需时间平均分别为相应算法的9.36 %与19.83 %，提高速度的效果非常明显，为分形图像编码算法提供了一个好的候选算法.