基于包络法的冗余机器人运动可靠性研究

2022-07-05丁力谷加辉周金宇康绍鹏陈逸飞李子依

兵工学报 2022年6期

丁力，谷加辉，周金宇，康绍鹏，陈逸飞，李子依

(1.江苏理工学院机械工程学院，江苏常州 213001；2.金陵科技学院机电工程学院，江苏南京 211169)

0 引言

机器替人是未来制造业的发展趋势，是实现工业智能化、数字化和自动化的保障。其中，工业机器人是智能制造的重要基石，它能显著提高生产效率、降低劳动成本[1]。实际生产中，机器人的制造、装配、疲劳磨损等因素会给本体带来几何误差[2]，从而导致末端执行器的实际轨迹与预定轨迹存在误差。另外，关节摩擦间隙、测量噪声及恶劣的服役工况也会进一步放大上述轨迹跟踪误差，从而降低机器人作业精度。机器人运动可靠性能够定量评估末端执行器实际位姿满足定位精度要求的程度，为评价机器人质量和修复机器人性能提供理论依据。

不确定性的描述方法主要包括概率法、区间数理论及模糊理论[3-4]。王伟等[5]考虑了尺寸误差和间隙误差对机器人运动轨迹的影响，基于4阶矩估计法得到了PUMA560机器人的位置可靠性，结果表明该算法比一次2阶矩估计法快了3～4倍，但结果精度易受样本数量的影响。潘敬锋等[6]综合了链传动、杆长和关节角3种误差因素，分别采用大数据法和试验法统计了随机变量分布特征，对喷涂机器人4种不同轨迹进行了可靠性分析，发现试验与仿真联合分析法具有更高的分析精度，缺点是只考虑失效概率密度最大点的误差，忽略了轨迹其他点造成的影响。文瑞桥等[7]将连杆长度、连杆转角和关节转角作为变量，利用包络法计算出了末端轨迹在3个位置上的时变可靠性，但没有分析不同误差精度对可靠性的影响。Wu等[8]采用稀疏网格数值积分法和鞍点逼近法，评估了工业机器人单坐标、单点、多点和轨迹精度的可靠性，通过4个仿真实例验证了该方法在精度和效率上的综合优势，不足之处在于该方法只适用于一些特殊的误差模型。张春宜等[9]等以柔性机器人为例，提出了基于智能算法的先进极值响应面法，研究了机器人动态可靠性，克服了极值响应面法求解可靠性效率慢的缺点，同时还保证了该算法在精度上与蒙特卡洛模拟(MCS)法相一致。

本文针对上述问题，采用包络法来分析机器人末端执行器的运动可靠性，并给出了评价综合位姿运动可靠度的指标。以7轴冗余机器人为例，分析连杆长度、连杆偏距和关节角对机器人末端轨迹的影响，采用1阶泰勒公式对误差函数近似处理，基于概率法获得末端失效模型，然后采用包络法将时变运动可靠性问题转换成时不变运动可靠性问题，通过多维正态积分计算出可靠性评价数值。通过仿真算例，验证了包络法计算机器人运动可靠性的可行性。

1 机器人运动学

本文研究的7轴冗余机器人虚拟样机如图1所示。图1中，X0、Z0为基坐标系，Xi、Zi(i=1～7)为第i关节的坐标系，X8、Z8为末端坐标系(机械手长度100 mm)，dj(j=2～7)为Xi-1移动到Xi的距离，a3为Z3移动到Z4的距离，a4为Z4移动到Z5的距离。

图1 7轴冗余机器人三维模型图Fig.1 Schematic diagram of 7-DOF redundant robot

采用改进的D-H参数法[10]获得机器人的结构参数，如表1所示。

表1 7轴冗余机器人的改进D-H参数Tab.1 Improved D-H parameters of 7-DOF redundant robot

表1中：θmax和θmin分别为关节角转动上限和下限，关节8为虚拟轴，实际上并不转动(θ8=0°)，其作用是更加快捷地得到机械手的位姿，从而便于实际操作。

相邻关节i-1到i的位姿变化可由齐次变换矩阵描述，即

(1)

根据正向运动学[11]可得机器人末端位姿矩阵为

(2)

式中：R为姿态矩阵；P为位置向量；x、y、z为机器人末端位置；rm1、rm2、rm3(m=1，2，3)分别为X8、Y8、Z8在基坐标系中的投影(Y8可根据右手准则建立)，代表机器人的姿态。

(3)

2 误差函数以及运动可靠性模型

2.1 误差函数

机器人运动可靠性可定义为其末端执行器在指定区间内实际输出的轨迹落在许用误差范围内的概率[12]。如图2所示：若机器人末端执行器轨迹(如青色曲线)控制在许用误差边界内则有效；若有超出误差带的情况(如红色曲线)则失效。

图2 机器人末端运动轨迹图Fig.2 Kinematic trajectory of robot end-effector

一般而言，几何误差是影响末端精度的主要因素，故本文借鉴文献[13-14]的研究成果，假设连杆长度、连杆偏距和关节转角存在几何误差，并且都服从正态分布，变量之间也相互独立，则末端执行器位姿误差描述为

gj(X,θ)=ψj(X,θ)-ψj(θ)

(4)

由于随机变量标准差的量级远小于各变量均值的量级，故误差函数可以通过1阶泰勒式[15]在X的均值μ处展开

gj(X,θ)≈aj0(θ)+aj(θ)·(μ-X)

(5)

将服从正态分布的X转化为服从标准正态分布的U，即

(6)

则(5)式可改写为

gj(U,θ)≈Lj(U,θ)=bj0(θ)+bj(θ)·U

(7)

式中：bj0(θ)=aj0(θ)；bj(θ)=(aji(θ)σi)n×1，aji为aj的第i个元素，σi为Xi的标准差。

2.2 运动可靠性模型

工程实际中，机器人的关节变量是与时间相关的，故可以将(4)式中的末端执行器位姿误差转换成与时间相关的函数。以末端执行器的x位置为例来阐述运动可靠性模型的推导过程。当运动时间t∈[to,te]时，设置运动的起始和终止时间分别为to和te，并指定运动公差为ε。当t∈[to,te]时，可定义x位置的运动可靠性模型为

Rx(to,te)=Pr{|g1(X,t)|≤ε,∀t∈[to,te]}

(8)

则其对应的失效概率模型可表示成

Pfa(to,te)=1-R1(to,te)=
Pr{|g1(X,t)|>ε,∀t∈[to,te]}

(9)

同理，可得机器人末端执行器的综合位姿可靠性模型为

(10)

机器人末端执行器的综合位姿失效概率模型为

(11)

3 包络法

3.1 包络方程

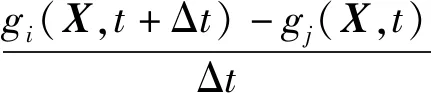
(12)

当Δt→0时，有

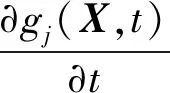
(13)

(14)

从(14)式第2个等式中，可得

(15)

将(15)式代入(14)式的第1个等式，可得

(16)

(17)

(18)

(19)

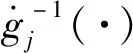
(20)

图3 Lj(U,t)=ε在的展开点Fig.3 Expanded points of Lj(U,t)=ε at

U可以改写成

(21)

式中：c为1个常数。将其代入(20)式的第1个等式，得

(22)

从而解得c为

(23)

(20)式的第2个等式变成

(24)

(25)

同理，G-(U)=0的表达式为

(26)

展开点为

(27)

(28)

为了使得可靠性模型更加精确，还要考虑to和te两个端点，则最终的运动可靠性模型为

(29)

(30)

3.2 可靠性评估

根据L(U,t)服从正态分布的特性，可靠性数值可以通过计算展开点的均值μL和协方差矩阵Σ得到：

R(to,te)=Φ(ε,μL,Σ)

(31)

式中：Φ(·)为标准正态分布函数；μL的计算公式为

μL=(s(tu)μL(tu))1×v=(s(tu)bjo(tu))1×v

(32)

协方差矩阵Σ的第c行第d列元素为

σcd=s(tc)s(td)b(tc)b(td)

(33)

需要说明的是，协方差矩阵Σ必须是正定的，并且行列式不能太庞大，否则不利于直接积分。当协方差矩阵Σ不满足上述条件时，可通过排除失效概率较小的冗余点使矩阵达到满秩状态[17]。失效概率的计算公式为

(34)

(35)

新的协方差矩阵Σ′的第c行第d列元素为

σ′cd=s(t′c)s(t′d)b(t′c)b(t′d)

(36)

最后，机器人末端执行器运动可靠性计算公式为

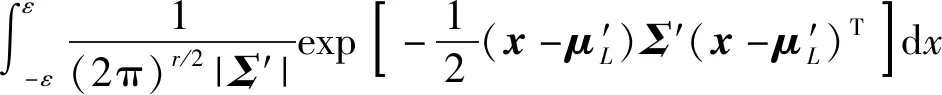
(37)

4 仿真算例分析

4.1 仿真条件

以7轴冗余机器人为例，模拟汽车天窗的装配任务，假设机器人起始位姿分别为Po=[525 mm，172 mm，-34 mm]T和Ao=[-121°,-31°,-21°]T，终止位姿分别为Pe=[611 mm，-93 mm，143 mm]T和Ae=[-174°，-69°，-16°]T，采用雅克比伪逆法[18]计算出起始和终止关节角分别为θo=[-150，229°，7°，134°，-121°，109°，37°]和θe=[-174°，195°，-11°，124°，-97°，84°，-2°]。进而利用5次多项式规划出2 s内的机器人关节角运动轨迹，并通过正向运动学获得机器人末端执行器从起始点到终止点的运动轨迹，如图4所示。

图4 机器人目标轨迹Fig.4 Robot target trajectory

为计算该轨迹的运动可靠性，需要结合冗余机器人3种变量的均值及其标准差，如表2所示。

表2 误差变量的均值和标准差Tab.2 Mean and standard deviation of error variables

以MCS法的计算结果为基准，引入等效极值法[19]与包络法比较，测试两种算法获得机器人运动可靠度的能力。仿真中，设定误差半径为1.4 mm，通过MCS法模拟2×105条末端执行器随机运动轨迹，并在图5中给出第2 s时刻的末端执行器位置误差图。从图5中可以看出，只有216个三维末端随机点落在了误差球外，表明所选取的误差半径较为合理。这里需要指出的是，通过这种方法可以获得合适的误差半径来确定仿真的初始条件。

图5 随机的末端点Fig.5 Random end points

4.2 运动可靠性验证

图6为3种算法获得的机器人末端执行器位置可靠度。从图6中可以看出，包络法与MCS法的求解结果基本吻合，而等效极值法相对其他两种方法精度略低，导致这种现象的原因是等效极值法只考虑了失效概率密度最大的点，忽略了轨迹其他点的失效情况。

图6 末端执行器位置可靠度Fig.6 Reliability of robot position

表3统计了3种算法在参考精度分别为0.2 mm、0.4 mm和0.6 mm时获得的机器人末端执行器位置可靠度。从表3中可以看出，随着参考精度的增大，3种算法获得的失效率降低，但包络法获得的失效率明显比等效极值法更接近MCS法的结果；当机器人末端位置方向上的参考精度为0.6 mm时，包络法较于MCS法的相对误差分别为1.2%、1.8%、0.4%，而等效极值法较于MCS法的相对误差分别24.0%、26.7%、29.4%。以上结果表明包络法在计算位置可靠度方面具有较高的准确性。

表3 位置可靠度Tab.3 Reliability of position

图7给出了包络法获得的机器人末端执行器运动失效率与对应MCS法获得失效率的差值。从图7中可以看出，包络法与MCS法的差值整体上随着位置参考精度的增加而变小，其中80%左右的数据都集中在±4×10-3区域，表明包络法的鲁棒性较好。

图7 包络法相对于MCS法的位置可靠度误差Fig.7 Position reliability error of envelop method

利用3种算法评估机器人末端执行器姿态运动可靠度，仿真结果如图8所示。从图8中可以看出，包络法获得的失效率曲线与MCS法基本一致，在参考精度为0°～0.06°范围内，包络法的求解精度要明显优于等效极值法。这可能是因为等效极值法在处理姿态运动可靠性时没有考虑点与点之间的相关性，从而导致了全局求解精度的下降。

图8 机器人姿态角可靠度Fig.8 Reliability of robot attitude

表4给出了3种算法在参考精度分别为0.02°、0.04°和0.06°时的姿态角失效率。数据显示各算法的失效率均随着参考精度的增长而降低，当参考精度为0.02°时，以MCS法的计算结果为基准，包络法获得姿态角失效率的相对误差比等效极值法分别低了3.9%、29.6%和10.1%。进一步说明相对于等效极值法，包络法具有较好的求解精度。

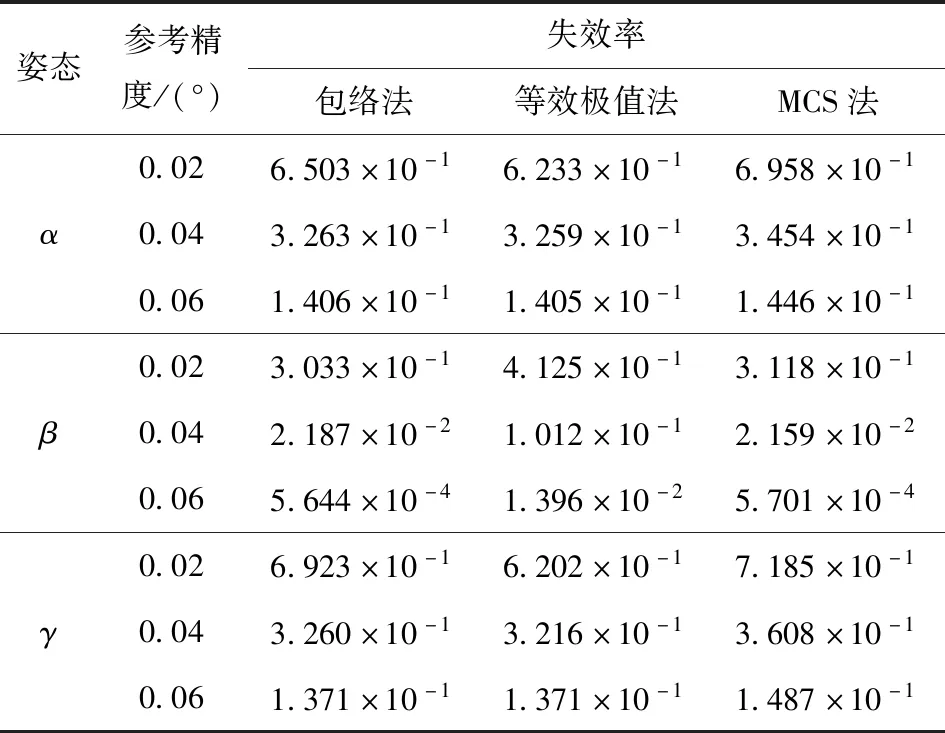
表4 姿态可靠度Tab.4 Reliability of attitude

图9为包络法与MCS法在参考精度为0.00°～0.14°范围内时获得的姿态运动失效率差值。图9中曲线表明，当参考精度为0.05°～0.12°时，包络法与MCS法的最大差值可达-4.5×10-2，但其余部分的差值都集中在-2×10-2～0内，表明了包络法具有较好的鲁棒性。

图9 包络法相对于MCS的姿态可靠度误差Fig.9 Attitude reliability error envelop method

另外，在评估机器人末端执行器运动可靠性时，MCS法所需计算时间为4 657 s，包络法所需计算时间为1 543 s，等效极值法所需计算时间为1 526 s。由此可以看出，包络法的计算效率虽不及等效极值法，但也与它接近，故在综合考虑计算效率和求解精度的前提下，使用包络法来评估机器人运动可靠性是较为合适的。

最后，用上述包络法求得关于时间的末端轨迹展开点来计算综合位姿可靠度。需要指出的是，姿态误差对综合位姿误差影响远不及位置误差，故接下来只分析综合位置可靠度。由于综合位置误差函数不服从正态分布，难以靠多维正态积分求得可靠性结果，故将包络法获得的位置展开点近似为综合位置误差的展开点，进而可通过(37)式计算出综合位置失效率。由于综合位置误差对应的协方差矩阵维度较高，采用直接积分法效率较低，故换用改进条件边缘乘积(I-PCM)算法[20]来提高运算速度，结果如图10所示。从图10中可以看出：在失效率大于0.4时，包络法与MCS法的差值随着失效率的降低而减小，而等效极值法与MCS法的差值随着失效率的降低而增长；在失效率小于0.4时，包络法与MCS法的差值为0～0.03，相对误差率为1%～42%，而等效极值法与MCS法的误差为0～0.15，其相对于MCS法的误差为39%～78%。以上结果表明等效极值法在求解综合位置误差上的精度远不如包络法。另外，尽管包络法在高失效率区与MCS法存在一定的偏差，但它在低失效率区内能表现出较高的求解精度。