基于复杂约束条件的欠驱动AUV三维路径规划

2022-07-05张家闻房浩霖李家旺

兵工学报 2022年6期

张家闻，房浩霖，李家旺

(宁波大学海运学院，浙江宁波 315211)

0 引言

海洋资源合理开发与国家经济发展关联密切，释放我国海洋产业发展动力和潜力的呼声持续高涨。自主水下航行器(AUV)作为海洋勘探的前沿载体，其系统平台的智能化已发展到新的高度。路径规划的技术水平可以表征AUV智能化程度。其定义是实时作业的AUV根据负载探测模块(侧扫声呐、前视避碰声呐等)及导航定位系统反馈的海洋环境信息，搜索出避绕水下障碍、连接始末点的全局路径。

现阶段，国内外AUV路径规划与自主避障技术研究持续发展。目前，AUV路径规划方法可归纳为如下三类：环境建模法(可视图法、维诺图法等)、智能化仿生学搜索法(粒子群优化算法、蚁群算法等)以及传统路径搜索法(A算法、人工势场法)。刘贵杰等基于水动力学建立AUV在海洋环境中移动时的受力模型，以最优能耗计算模型为评价因子改进传统蚁群算法，在兼顾收敛速度的同时保障了AUV自主规划避障路径。姚鹏等在区域洋流恒定的条件下，基于传统人工势场法提出一种导航向量场法，引入修正矩阵对初始导航向量场进行修正，量化海洋环境中障碍物对向量场的影响同时得到修正导航向量场，结合AUV运动速度模型解决避碰动静态障碍物的问题。张楠楠等在传统蚁群算法的基础上加以改进，将并联路径能耗与路径光滑度作为指标设计评价函数，对种群适应度进行评价。但算法运行时疏于考虑路径曲率连续问题，导致路径跟踪存在困难。Raheem等在算法规划行驶路径的基础上，筛选路径控制节点结合样条曲线理论拟合路径，在保留路径形状特性的前提下得到曲率连续的路径曲线。然而工作环境停留在二维范畴，未将三维环境的复杂性与航行器内外约束因素联合分析。

本文选择障碍物有限的海洋浅水区域进行研究，考虑AUV实时作业的特殊性，并忽略海流对AUV的影响，基于欠驱动AUV约束条件进行分析。然而，传统智能化仿生学算法与欠驱动AUV路径规划存在适配度低、可行性差的技术问题。为有效解决算法适配问题，本文基于两个方面创新改进。针对运动约束，确定规划路径方法中需要引入的影响因子，从逼近程度、崎岖程度及垂直面安全域3个范畴改进传统蚁群算法，提高寻径搜索能力，同时避免局部路径最优及规划失效。针对终端约束，本文提出速度回转球相切方法重规划路径末端区域，在保留原路径轨迹信息的同时，限定末端曲线轨迹以满足终端速度矢量约束。联合B样条曲线理论对路径点拟合处理，得到曲率连续的全局路径。最后将算法在模拟海域环境中仿真，证明了算法有效性与鲁棒性。

1 问题描述

欠驱动AUV在进行空间路径规划时，由于航行器自身运动能力及海底环境结构的特殊性，致使在设计寻径算法之前，应先分析约束因素及空间环境建模。

1.1 运动约束

由于驱动装置的舵轮和推进器直接控制欠驱动AUV的运动位置和姿态，欠驱动AUV在横移和潜浮两个自由度的运动没有直接驱动力，导致AUV的位置控制困难，因此路径规划时需要考虑AUV运动及操作特性，增强路径的可跟踪性。

全局路径轨迹生成受到AUV最小回转半径与潜浮角的限制，约束条件如下：

(1)

式中：()为路径点的回转半径，为路径节点；()为潜浮角变化函数；为相应物理量求得的最小回转半径；为最大潜浮角。

1.2 终端约束

由于航行器抵达终端目标点时触发回收指令或衔接次级工作任务，AUV的姿态角度也是规划终端目标点时考虑的因素。本文假设欠驱动AUV以特定的速度矢量进入终端目标点，引出终端速度约束，约束条件表达式如下：

()=

(2)

式中：()为AUV到达目标点时的速度矢量，为路径终端目标点；为特定速度矢量。

1.3 空间海域建模

为合理处理数据信息集以确保路径规划可行性，需要对已知海域进行环境建模。运用栅格法以定精度对已知海域环境空间划分，将地质障碍物信息数字化抽象模型，以便于计算机操作，得到等间距栅格地图，如图1所示，其中为工作空间的原点，轴、轴、轴分别为横向、纵向及垂直方向。

图1 空间区域栅格划分Fig.1 Grid division of space region

将面按照给定精度分隔出×个栅格，与分别代表轴、轴方向的划分精度值。各栅格的顶点代表AUV作业时能够抵达的空间路径点。将面的栅格点沿着轴方向延伸并贯穿整个工作空间，得到×个长方体。基于海底地质形态的空间坐标值，各长方体沿轴方向能够实现任意精度下垂直方向无碰撞的路径搜索。基于海域环境模型与路径生成约束因素，设计算法完成全局路径规划。

2 路径规划算法

传统蚁群算法的并行正反馈特性赋能算法具有寻优能力强、鲁棒性高的优势，但面对大体量问题时，算法迭代时间长、精度低，容易陷入局部最优。因此，改进算法模型及参数是适配欠驱动AUV路径规划的关键。

2.1 算法函数设计

211 安全域设计

由于障碍物的位置可能位于栅格相邻节点之间，如图2所示法平面的障碍物界面位置。

图2 Oyz截面的障碍物局部轮廓Fig.2 Local contour of obstacle in Oyz

按照定步长规划的全局路径将会造成垂直方面避碰冗量过大、能耗增加，甚至潜浮角超过约束极限，导致路径无法有效跟踪。为解决上述问题，本文提出垂直方向的变步长路径搜索规则，如(3)式所示：

=(,)+Δ

(3)

式中：为垂直方向的步长；(,)为障碍物高度值；(,)为备选路径节点在面的坐标值；Δ=12代表安全域值，为AUV艇体长度。垂直面的变步长设定提高了寻径时的避碰精度，使规划出的路径具有高平缓度、低偏离性的特性，工程中具有增加航行器使用寿命、节约成本的经济价值，有效满足AUV勘探信息的作业目的。

212 启发函数改进

传统蚁群算法进行路径规划时，算法迭代过程中的启发值与采样点的距离有关。启发函数影响因素过少，将导致状态选择条件局限，造成路径陷入局部最优甚至寻径失效，因此本文的启发函数设计如下：

(4)

式中：(,,)为算法启发函数；、、分别为距离影响因子、逼近度影响因子、崎岖度影响因子；、、为相应影响因子的权重系数。

距离影响因子表示当前点与备选点之间距离对转移概率的影响，

(5)

式中：‖,‖为点到点向量,的二范数。越大，蚂蚁越倾向于选择距离短的目标点。相比于二维情况，规划三维路径时蚂蚁可选择的目标点更多，情况更复杂，仅考虑距离影响因子将导致搜索路径偏离终点。因此引入逼近度影响因子(,,)来限制路径偏移，

(6)

式中：Δ=-表示终点的纵坐标与备选点的纵坐标的差值，体现了蚂蚁由横向顺次选择目标点时纵向上目标节点与终点的逼近程度，以保证规划路径的平滑性。

为减少AUV舵轮的转动次数与幅值，构建崎岖度影响因子(,,)以保证路径的平滑性，具体形式如下：

(,,)=2-05(〈(,),(-1,)〉+
〈(,),(-1,)〉)

(7)

式中：(,)与(,)分别表示路径节点向量,在水平面与垂直面的投影向量；〈,〉表示向量间夹角的弧度值。

213 信息素更新

信息素修正启发值来引导单个蚂蚁在循环中寻找更优路径节点，传统蚁群算法中信息素仅在单次循环后进行全局更新，一定程度上割裂了蚂蚁之间的启发交流，弱化了单个蚂蚁的全局搜索能力。为解决寻径缺陷，信息素的更新方式如下：

(8)

式中：为迭代次数；为当前迭代中的蚂蚁编号；为全局信息素衰减系数，决定了每次循环后各路径上信息素的衰减量，∈[0，1]；表示每代蚂蚁未经过的路径点上的信息素衰减量，其数值决定算法收敛速度，值越大，算法收敛越快，易陷入局部最优解，反之强化蚂蚁的搜索能力；Δ为最优个体信息素释放量，

(9)

为单个蚂蚁信息素浓度值，min(())表示截止到第代循环，完成路径搜索的蚂蚁最小适应度函数值，适应度函数的性能指标为路径长度与平滑度的结合，用以判断单个蚂蚁规划路径的优劣，评价是否满足潜浮角约束限制。

由于蚂蚁在垂直面方向以变步长寻径，本文将单位栅格体垂向棱边上任意一点(上端点除外)的信息素设为等值，以满足蚂蚁垂向搜索特性。

3 路径生成规则

经过蚁群算法迭代计算后搜索出一系列路径点集合，连接路径点(∈)得到直线段可行路径。由于直线段路径曲率不连续，跟踪实现困难。因此，需要基于AUV运动及姿态约束对路径控制点进行拟合优化，使其具有更高合理性。

3.1 终端速度限制

为满足AUV进入路径终点的速度约束以衔接其他工作任务，需要对路径点集合的末端区域(，)进行重规划(为终点前一路径点)。由于目标点速度矢量特定，周围零障碍物空间有限，AUV回收进坞的直线衔接技术存在局限性，本文提出速度回转球相切的方法，收缩AUV运动空间，以降低碰撞危险系数。

假设路径点集末端两点(，)的空间连线为AUV驶向目标点的速度矢量，=(0,||,0)为AUV经过终端目标点时的速度矢量方向。经过速度矢量的任意平面能够确定两个相切球，半径为最小回转半径。两个速度矢量确定4个切球，两两相切有4种位置情况。为保证AUV在两相切球面上回转连续性，两球心应在同一平面内。

(10)

AUV以速度进入相切球曲线轨迹开始回转时，速度与回转球的切点为AUV行进的中间辅助点。两切球球心、的连线为2倍回转半径，通过空间几何运算，联立球心半径2的空间球方程解出中间辅助点=(,,)。经过环绕两相切球行迹，按预置速度到达终端点，具体实现如图3所示。

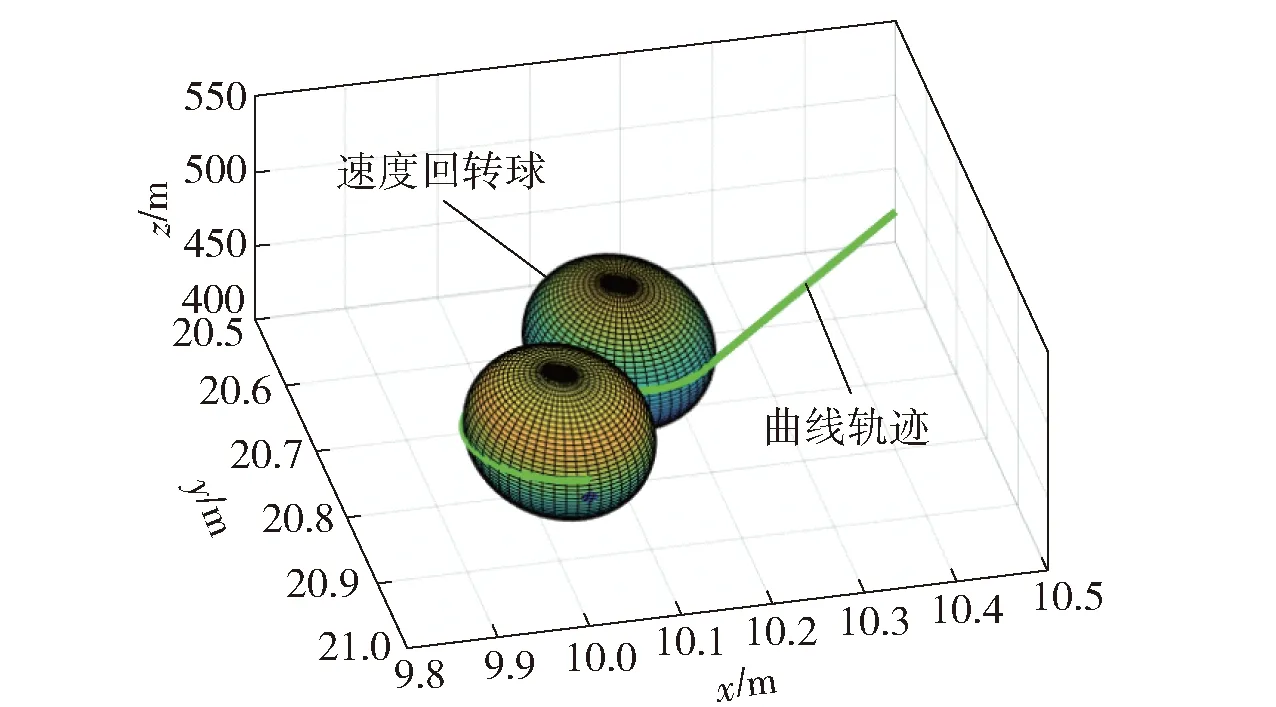
图3 回转半径球相切轨迹Fig.3 Tangent trajectory of two balls at turning radius

3.2 B样条曲线拟合规则

利用3次B样条曲线方法拟合全局路径，其曲线局部性满足改变中间型值点仅变更局部曲线形状，不影响整体拟合曲线轨迹，匹配AUV局部动态避障的要求，如图4所示。

图4 改变中间型值点的B样条曲线拟合Fig.4 B-spline curve fitting with changed points

拟合路径由有限分段曲线顺次首尾拼接而成，限定拟合路径的曲线形状，确保路径同时满足曲率连续及约束因素。B样条曲线的方程如下：

(11)

式中：()为B样条曲线的分段形式；()表示B样条曲线的基函数；,为第段曲线的第个控制点。

每段样条曲线由4个控制点与基函数根据自变量区间结合运算生成。路径点集合的起始点与目标点分别为、，路径曲线在空间中的轨迹需要经过指定控制节点，以引导AUV按照预设速度矢量经过目标终点。利用B样条曲线的固有特性，采取三重点方法对与中间辅助点加以控制。

(12)

综上所述，路径点集提供B样条曲线拟合的型值点，衔接样条曲线与切球轨迹以完成路径规划的所有步骤。

3.3 算法实现流程

结合改进蚁群算法的参数设计与B样条曲线的拟合特性，路径规划算法实现整体实现流程图如图5所示。

图5 算法具体流程Fig.5 Flow chart of algorithm

根据算法框架及思路，改进蚁群及B样条拟合算法实现的伪代码结构如下：

:environment_data

:optimal_path

Phase Ⅰ Initialization

1 # 初始化参数

2 load environment_data

3 popnumber ← population of ant

4 pher_ant ← initial pheromone；

5 iter_max ← max iteration

6 delta_x ← step length indirection

7 delta_y ← step length indirection

Phase Ⅱ Path planning based Advanced ACO

8 # 改进蚁群算法寻找最优路径

9 for== 1:iter_max

10 function search_path(parameters)；

11 function cacufit(parameters);

12 function update(parameters);

13 if== 1

14 [path，pher_ant]=search_path(paramters);

15 fitness=cacu_fit()；

16 [bestfitness，best_index]=min(fitness)；

17 bestpath=path(bestindex,:)；

18 BestFitness=[BestFitness；bestfitness]；

19 else

20 repeat

21 end

22 end

23 # 信息素更新

24 for== 1:size(path)

25 pher_ant=update(pher_ant)

26 end

Phase Ⅲ Path re-planning and trajectory fitting

27 #路径末端区域重规划，得到相应几何参数

28 function re_plan(parameters)；

29 function curve_fit(parameters)；

30 [，，，sphere_core1，sphere_core2，tangency，

31 control_point] = re_plan(parameters)

32 #路径控制点的曲线拟合

33 for== 1 :size(control_point)

34 fitting_path = curve_fit (parameters)

35 end

4 仿真

为验证本文算法的有效性，选取某型AUV(艇体长度=12 m，最小回转半径=25 m，最大潜浮角=0.223 rad)对其进行仿真。首先导入某海域海底空间结构，通过障碍物相对高度及轮廓峰值结合自然插值法获得数值点集，栅格划分AUV工作空间。初始化起始点和目标点，设计预置算法参数值如表1所示。

根据表1中的参数编辑算法运行仿真，仿真结果与文献[6]算法及传统蚁群算法运行结果进行对比，如图6(a)所示，在3种算法均有效规划路径的前提下，可以看出本文算法成功地规划出了一条光滑的曲线路径，连接起始点与目标点，规避了曲率不连续、转角过大的问题。

表1 路径规划算法参数取值Tab.1 Parameter values in path planning algorithm

图6 路径规划对比图Fig.6 Comparison chart of path planning

对比路径局部图6(b)可知：本文算法规划出的路径在精确经过目标点的同时保证了AUV终端速度()==(0，1，0)，符合终端约束条件；文献[6]算法速度矢量与的偏差值为0611 rad。同时对比潜浮角可知，本文算法规划出的路径的潜浮角始终保持在=0.223 rad的极限范围内(见图6(c))，确保了实际工作中AUV路径跟踪的可实现性。图6(d)展示了本文算法迭代过程中适应度函数的收敛情况，在算法迭代计算初期，适应度值下降速率快，具体数值由适应度函数结合算法参数值计算得出，中期不断替换最优种群个体参数，更新适应度值，在第26次迭代中找到了全局最小适应度值，完成收敛。

表2为3种算法在路径距离及转角的数据对比。由表2可见，本文算法所规划的路径总距离为27.43 km、总转角值为18.76 rad，相比文献[6]算法与传统蚁群算法，在算法性能方面均有提升。