基于概率密度演化方法的火炮输弹过程不确定性分析
2022-07-05王明明钱林方陈光宋刘太素
王明明,钱林方,2,陈光宋,刘太素
(1.南京理工大学 机械工程学院,江苏 南京 210094;2.西北机电工程研究所,陕西 咸阳 712099;3.南京工程学院,江苏 南京 211167)
0 引言
输弹机是大口径火炮的重要组成部分,其作用是将弹丸从输弹出发位置沿炮膛轴线方向快速、可靠地推送到炮膛内。输弹过程包括强制输弹过程和惯性输弹过程,强制输弹过程是指弹丸在推弹板强制推动下沿炮膛轴线方向向前运动,直至弹丸底部脱离推弹板;惯性输弹过程是指弹丸底部与推弹板脱离,在惯性作用下卡进坡膛。由于输弹系统中存在输弹机齿间间隙、推弹板速度、弹丸惯量等大量随机因素,导致输弹结束时弹丸速度和姿态存在不确定性,影响弹丸的卡膛一致性,进而通过火炮发射过程的传播影响射击精度。因此,对输弹过程进行误差传递分析,开展输弹过程参数不确定性对输弹一致性的影响研究,对进一步提高输弹一致性、提升火炮射击精度有着重要意义。
随着火炮自动化的发展,国内相关学者对输弹过程进行了研究。赵森等以试验为基础,分析研究了恒定输弹力对初速的影响,提出了改进措施。薛百文等通过弹丸受力分析建立运动方程,研究了底盘运动状态对弹丸在惯性输弹段的影响。刘朋展等针对弹丸姿态影响输弹可靠性与一致性问题,分析了影响弹丸姿态的因素。近年来,学者们开始更多地关注参数不确定性对输弹结果的影响。李伟等考虑随机参数漂移,探讨了供输弹系统的动作可靠性问题。高学星等提出了一种间接提高弹药协调器定位精度可靠性的优化方法,具有较好的优化效果和较高的计算效率。刘太素等考虑输弹协调机构中的众多不确定性参数,提出了基于稀疏多项式混沌展开(SPCE)- 高维模型表示(HDMR)的稳健优化方法,实用有效。林通等基于ADAMS软件建立考虑参数随机性的输弹过程动力学模型,进行了输弹机稳健优化设计研究。张弘钧等基于区间参数的不确定性分析方法对某大口径火炮输弹一致性进行研究,认为影响输弹一致性的主要因素为惯性阶段的参数不确定性。相关研究结果为分析参数不确定性对输弹过程一致性的影响提供了重要参考。然而,如何考虑更多的参数以及提高分析的计算精度是需要进一步研究的热点问题。针对不确定性参数数量众多、计算效率低下的问题,发展一种考虑高维不确定性参数的输弹不确定性分析方法,有助于进一步量化不确定性参数对输弹过程的影响,也可为提高卡膛一致性研究提供良好的基础。
输弹过程的不确定性分析在理论上属于不确定性传播问题,常采用概率类不确定性分析方法进行研究,其数学理论较为完善且不确定性量化和传递的推导也更加准确便捷。概率方法通过随机变量对不确定性进行描述分析,最经典的即蒙特卡洛(MC)方法,具有精度高、适用范围广的优点,但其计算量庞大,一般仅用于验证结果的准确性。实际上,大多概率类方法如代理模型、函数展开、降维积分等都是基于系统响应的统计矩计算其概率密度函数,随着参数数量的增加,将面临计算量庞大、高阶矩计算精度不足、概率分布拟合不准确等问题。概率密度演化方法(PDEM)通过引入扩展状态向量构造复合系统随机动力学方程,建立系统响应的概率密度演化方程,直接积分求解系统响应的概率分布,精度高且对样本量需求小,可以有效避免“维度灾难”的发生。实际中,输弹过程涉及到的不确定性参数较多,基于概率密度演化方法对其进行不确定性分析是较好的选择。
本文通过分析某火炮输弹机的结构与原理,利用ADAMS软件建立输弹机动力学模型,推导了输弹响应的概率密度演化方程,进而通过Lax-Wendroff格式的有限差分法进行求解。将仿真结果与文献[20]试验结果对比,验证了模型的准确性;将PDEM与MC方法进行对比,验证了PDEM的适用性;对不同工况下的输弹过程不确定性传播进行了分析。
1 输弹过程动力学建模
本文以某中大口径火炮齿轮- 齿条式输弹机为研究对象,对其进行动力学建模。
1.1 基本假设
为便于建立输弹机动力学模型,分析输弹过程,做如下假设:
1)在输弹过程中弹丸不变形,可将其简化成6自由度刚体;
2)将弹丸与托弹板、炮尾以及身管的碰撞考虑为弹性接触碰撞;
3)协调到位后无其他外部激励,输弹机与身管相对于地面保持固定。
1.2 输弹过程动力学建模
输弹机包含协调油缸、输弹油缸、齿轮、托弹板、推弹板、协调臂箱体等机构,具体结构如图1所示。协调臂的一端安装在耳轴上,协调油缸筒端与架体相连,协调油缸杆端与协调臂相连,三处连接均可旋转;箱体固定在协调臂上,输弹油缸整体安装在箱体内,油缸筒端固定在箱体上,油缸杆与齿轮轴固连;齿轮通过轴承与齿轮轴连接,同时与上下两根齿条啮合,上齿条固连在托弹板上,下齿条与箱体固接;托弹板上有抱锁装置,用于防止弹丸掉落。

图1 输弹机结构图Fig.1 Structural view of ammunition ramming mechanism
根据输弹机结构以及各部件之间的约束关系,可分析得到输弹机拓扑关系如图2所示。
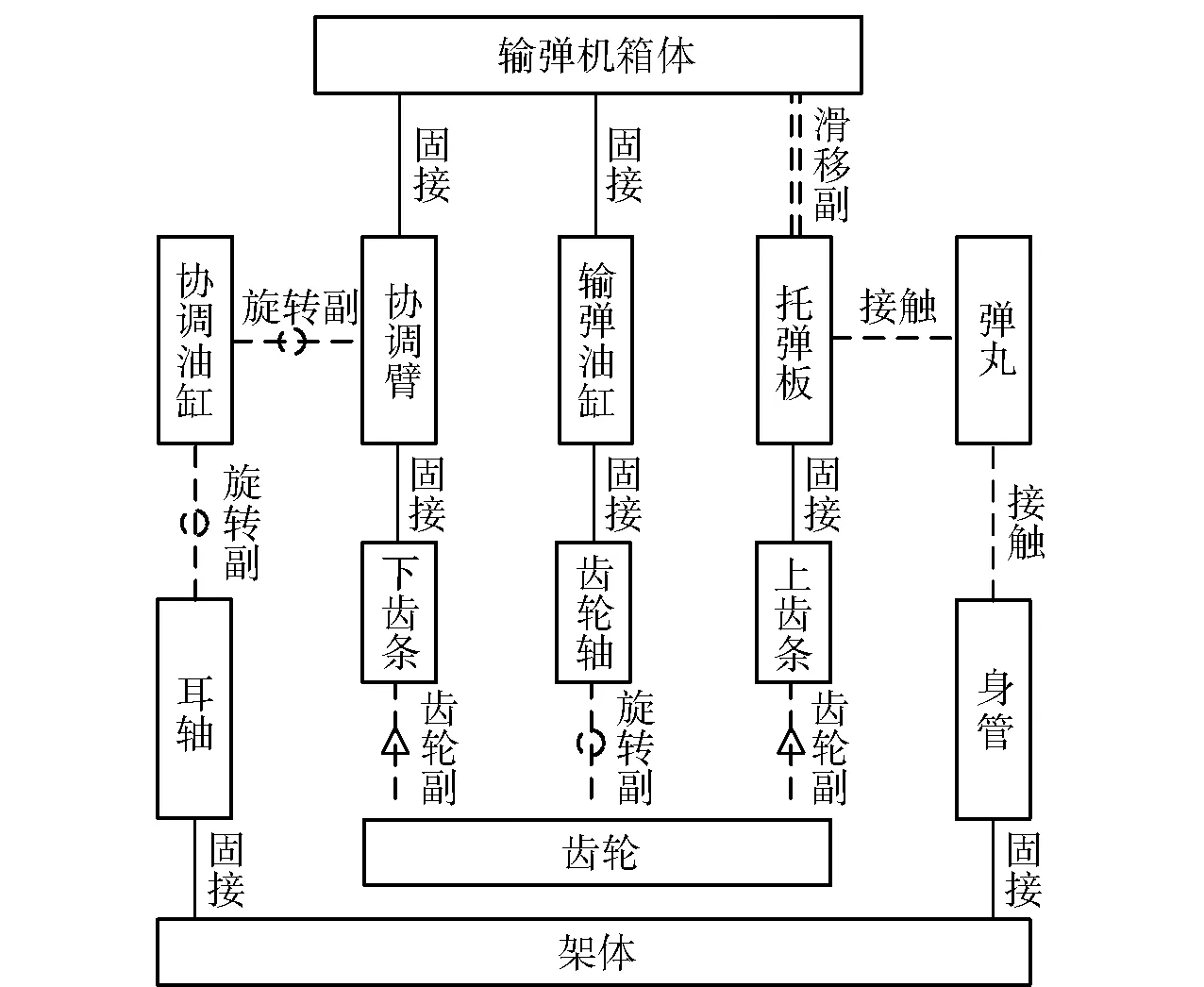
图2 输弹机拓扑结构Fig.2 Topological structure of ammunition ramming mechanism
输弹机原理如下:通过电控输弹油缸推动齿轮轴向身管方向平移,由于与齿轮啮合的上下齿条分别固连在输弹机箱体和托弹板上,而输弹机箱体相对于地面固定不动,故此时承载着弹丸的托弹板向前平移运动。具体过程又分为强制输弹和惯性输弹两部分,强制输弹是指弹丸在托弹板的推动下向前加速平移运动达到最大速度的过程,惯性输弹是指弹丸不再受到托弹板的推力作用,而仅靠惯性向前运动直至与托弹板分离,继而飞入炮膛完成卡膛的过程。其中,强制过程中弹丸与托弹板相对静止,是一个简单加速运动过程;惯性过程中首先是弹丸在托弹板摩擦力与重力作用下作半约束惯性运动,其次是仅受重力作用的惯性飞行阶段,最后是重力、炮膛摩擦力以及坡膛碰撞力作用下的膛内运动阶段。
当弹丸与托弹板、身管坡膛发生摩擦时,摩擦力以滑动摩擦为主。考虑到输弹过程中的弹丸速度一般不超过5 m/s,属低速摩擦,符合如下摩擦力经典公式:
=
(1)
式中:为摩擦力;为接触正压力;为摩擦系数,可以直接按照黄铜- 钢的摩擦系数设定弹带与托弹板、身管坡膛的摩擦系数,按照钢- 钢的摩擦系数设定弹丸定心部与托弹板、身管坡膛的摩擦系数。
当弹丸与托弹板以及坡膛发生接触碰撞时,按照弹性碰撞假设可直接引用Hertz接触定律计算其接触刚度

(2)
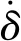

(3)
、分别为两个物体在接触点的曲率半径;、为两种材料的泊松比;、为两种材料的弹性模量。
输弹开始时,弹丸在重力作用下静止在托弹板上,弹底与推弹板接触,弹带、定心部与托弹板接触;然后通过输弹油缸施加载荷压力,推动齿轮- 齿条运动,进而带动托弹板、弹丸向前运动,直至弹丸抵达卡膛起始位置。参考基本假设,本文根据某型中大口径火炮输弹机构尺寸利用ADAMS软件建立输弹过程动力学模型如图3所示,该系统可输出弹丸的位移、速度和加速度曲线等。
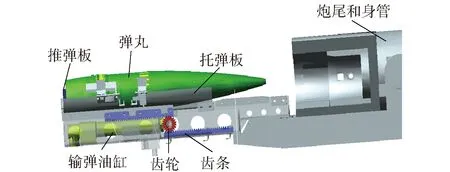
图3 输弹机ADAMS模型Fig.3 ADAMS model of ammunition ramming mechanism
2 输弹过程概率密度演化方程及求解
2.1 输弹过程概率密度演化方程
实际工程中影响输弹精度的不确定性因素众多,为方便建模分析,可将输弹过程涉及到的不确定性因素简单分为2类:系统随机参数和输入随机参数。由于本文研究对象是一种弹射式输弹机,故系统随机参数主要指弹丸和输弹机的物理、几何参数,具体包括弹丸的质量、质心位置、3个方向的转动惯量、前定心部半径、前定心部与托弹板间的摩擦系数、弹带半径、弹带与托弹板间的摩擦系数、托弹板半径、托弹板轴线与身管轴线的倾角以及竖直距离,共12个参数;输入随机参数即输弹油缸的压力参数,主要包含最大加载压力、最大压力时刻、最小加载压力、最小压力时刻,共4个参数。
考虑上述不确定性参数,可将输弹随机动力学方程表示成如下形式

(4)

令=[,],记其联合概率密度函数为(),可见同时包含了输弹过程中的16个随机参数,则弹丸响应可表示如下:
=(,)=[(,),(,),…,(,)]
(5)
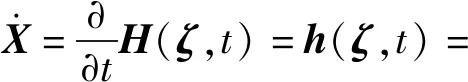
(6)

由(4)式可知,上述输弹随机动力学方程包含了输弹过程中的所有随机因素,可以看作一个保守的随机系统,符合概率密度守恒原理的描述。因此,输弹过程中的弹丸随机响应与随机变量的联合概率密度函数(,,)应满足广义概率密度演化方程,可写成如下形式:

(7)
即输弹过程广义概率密度演化方程。
2.2 方程求解
常用的边界条件为
(,,)|→±∞=0,=1,2,…,6
(8)
初始条件为
(,,)|=0=(-)()
(9)
式中:(·)为狄拉克函数;为初始时刻的弹丸状态变量值,即弹丸在托弹板上达到静平衡时的位姿参数。由于弹丸静置在托弹板上时仅弹底与托弹板接触、前定心部和弹带与托弹板接触,故可以根据弹丸、托弹板尺寸直接计算。若以托弹板轴线与推弹板交点为坐标原点,弹丸前进方向为轴方向,轴方向垂直轴向上,轴方向由右手法则确定,则=[0344 3,-0588 3,0,0,-1004,0]。
求解(7)式可得到的概率密度函数:

(10)
式中:为随机变量的参数空间。
特别地,当只关心第个响应时,对(,,)求除以外的多重积分,得到如下边缘概率密度
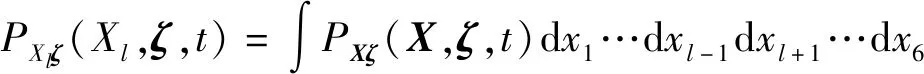
(11)
同理,对(7)式进行多重积分,得

(12)
由此可见,当考察的物理量为某单一响应时,其与随机参数的联合概率密度函数(,,)关于时间的变化率与关于空间的变化率呈正比,比例系数由该项位移响应的瞬时速度决定,体现了输弹过程中概率演化与物理演化之间的内在规律。
(12)式是1阶偏微分方程,由于无法给出显式的表达式,只能通过数值算法进行求解。对随机参数进行采样后获得一系列确定值,此时(12)式可以写成

(13)
(13)式符合1阶偏微分方程的一般形式

(14)
式中:(,)看作(13)式中的联合概率密度函数;()为速度项;为位移项。此时可直接采用有限差分法对其进行求解。
首先对状态空间域和时间域进行离散化,
=·Δ;=0,±1,±2,…
(15)
=·Δ;=0,1,2,…
(16)
式中:Δ、Δ分别表示空间离散步长和时间离散步长;为第步的空间坐标;为第步的时间坐标,不同的离散化格式对应不同的差分格式。
本文采用如下基于中心差分格式的Lax-Wendroff格式:

(17)

同时,为了计算的收敛性和稳定性,空间以及时间离散步长的选取还需始终满足
0<|()|≤1
(18)
这样才能保证数值计算的传播始终收敛,即著名的Courant-Friedrichs-Lewy(CFL)条件。
综上,本文采用基于Lax-Wendroff格式的有限差分算法计算输弹过程弹丸响应分布情况,具体步骤如下:
在输弹过程随机变量的参数空间内选取样本点。根据各随机变量的分布类型及统计信息,利用拉丁超立方采样选取个离散代表点集={,,…,,…,},并计算每个代表点的概率权重,又称赋得概率。

建立时空差分网络,利用基于Lax-Wendroff格式的有限差分法求解(12)式,得到第个弹丸响应的第(=1,2,…,)条轨迹的边缘概率密度函数,(,,)。
累计求和,将步骤3中的边缘概率密度函数累加,得到第个弹丸响应随时间演化的概率密度函数

(19)
3 输弹过程不确定性分析
3.1 输弹模型验证
通过试验测量某大口径车载火炮在30°射角时的输弹油缸压力随时间变化的曲线,结果如图4(a)所示,油缸压力变化大体分成两个阶段,即首次加载- 卸载阶段以及二次加载- 稳定阶段。实际输弹过程中,弹丸往往在油缸首次加载- 卸载阶段即获得最大速度,之后伴随着托弹板减速,弹丸底部与推弹板分离,进入惯性输弹阶段。

图4 30°角输弹压力曲线Fig.4 Pressure curve of ammunition ramming at 30°
为方便研究与建模加载,本文将输弹压力简化为线性加载过程,如图4(b)所示,、分别为首次加载、卸载的结束时间,、分别为首次加载、卸载结束时的压力值,这4个参数就是4个输入不确定参数。
为验证输弹机模型的准确性,将图4(b)中的简化油缸压力曲线加载到ADAMS模型中,输出弹丸轴向位移随时间变化的曲线,并与试验测试结果进行对比,结果如图5所示。测试结果仅包含弹丸在1 m以内的变化曲线,主要是由于试验中所用到的激光位移传感器量程有限;尽管如此,图5中的弹丸仿真位移曲线与试验结果在有限范围内还是非常吻合的,这也恰好验证了输弹机ADAMS模型的准确性。

图5 30°偏角输弹时的弹丸轴向位移仿真与试验结果对比Fig.5 Comparison between simulated and test results of projectile axial displacement at 30°
3.2 方法适用性验证
在输弹过程的系统随机参数中选取12个代表性参数作为本文的研究重点,其统计信息相对更加容易获取,对输弹结果的影响相对也更为显著。具体的参数统计信息如表1所示。

表1 输弹过程中的系统参数不确定性Tab.1 Uncertainty of system parameters during ammunition ramming
此外,由于输弹与卡膛过程是火炮发射的前两个连续阶段,没有明确的界面,本文设置弹丸轴向位移达到坡膛前的某一点时输弹仿真结束,认为此时的弹丸状态变量值即输弹动力学模型的输出,同时也是后续卡膛过程的输入。
考虑到输弹过程,尤其是惯性输弹阶段弹丸进入内膛后的运动状态参数难以测量,这里选择与蒙特卡洛方法的计算结果对比来验证上述方法的有效性。以0°输弹角为例,仿照图4中的简化方法,根据0°角输弹压力测试得到系统输入的参数不确定性如表2所示。

表2 0°角输弹时的输入参数不确定性Tab.2 Uncertainty of input parameters in ammunition ramming process at 0°
同时考虑这16个系统随机变量和输入随机变量,分别通过MC方法和PDEM计算输弹结束时的弹丸概率密度函数。其中,MC方法通过拉丁超立方抽样方法直接采样10 000组进行仿真计算,对结果统计得到弹丸响应的概率密度函数;PDEM则按照3.2节的步骤,利用概率密度演化的方法采样500组样本点,同样可以计算获得弹丸响应的概率密度函数。以弹丸轴、轴方向的位移和自转角为对象,分别计算其概率密度函数,结果如图6~图8所示。

图6 拟合概率密度- 弹丸y轴方向位移曲线Fig.6 Projectile displacement in y direction
由图6、图7可以看出:0°角输弹时的弹丸轴方向位移明显偏大,这是重力作用的结果;但轴、轴方向位移的波动范围是接近的,其概率密度函数均为单峰分布,而通过PDEM拟合的概率密度函数曲线与MC方法统计结果几乎一致,仅在边缘以及峰部存在微小误差。图8所示为拟合概率密度函数- 弹丸轴方向偏角曲线。由图8可见,0°角输弹时弹丸自转角的概率密度函数是双峰分布,PDEM较为准确地拟合出双峰趋势,曲线也基本吻合。

图7 拟合概率密度- 弹丸z轴方向位移曲线Fig.7 Projectile displacement in z direction

图8 拟合概率密度- 弹丸x轴方向偏角曲线Fig.8 Spin angle of projectile in x direction
获得概率密度函数,不仅可以直观判断弹丸响应的具体分布情况,还可以进一步分析其统计特性。根据概率密度函数计算弹丸响应的前2阶原点矩如下:

(20)

(21)
式中:E(·)表示期望。进而有
=E()
(22)
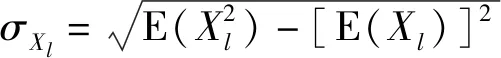
(23)
式中:为的均值;为的均方差。弹丸响应统计特性结果如表3所示。

表3 弹丸响应统计特性Tab.3 Statistical characteristics of projectile response
概率密度演化方法仅通过500组样本即可准确地拟合出输弹响应概率密度函数的趋势,无论是单峰还是多峰,这是通过低阶矩拟合概率密度函数的方法无法比拟的,表明其对于输弹过程高维不确定性分析问题的适用性。另一方面,表3对比了该方法的计算精度,仅需500组样本点即可获得误差不超过5%的均值、均方差,在保证高效率的同时又满足了工程实际需求。
3.3 输弹过程的概率密度演化
为更加全面地分析参数不确定性对输弹过程系统响应的影响,以0°、30°以及51°输弹角为例,直接通过概率密度演化方法拟合弹丸响应的概率密度函数,进行不确定性分析。系统参数统计特性仍见表1,0°输弹角时的输入参数不确定性见表2。表4、表5分别给出了30°、51°输弹角时的输入参数不确定性。

表4 30°角输弹时的输入参数不确定性Tab.4 Uncertainty of input parameters in ramming process at 30°

表5 51°角输弹时的输入参数不确定性Tab.5 Uncertainty of input parameters in ramming process at 51°
影响弹丸卡膛的主要因素是弹丸的位置、姿态以及卡膛速度,故本节以弹丸在轴、轴方向的位移、偏角以及轴方向的速度为对象,拟合的概率密度函数如图9~图13所示。

图9 拟合概率密度- 弹丸y轴方向位移曲线Fig.9 Projectile displacement in y direction

图10 拟合概率密度- 弹丸z轴方向位移曲线Fig.10 Projectile displacement in z direction

图11 拟合概率密度- 弹丸y轴方向偏角曲线Fig.11 Deflection angle of projectile in y direction

图12 拟合概率密度- 弹丸z轴方向偏角曲线Fig.12 Deflection Angle of projectile in z direction

图13 拟合概率密度- 弹丸x轴方向速度曲线Fig.13 Velocity of projectile in x direction
与16个不确定性参数相似的是,对应3种输弹角的弹丸响应分布都是对称的,都属于单峰类正态分布。图9~图12表明,随着输弹角的增大,弹丸位置、姿态的波动愈大,弹丸轴线与身管轴线的偏差增加,卡膛一致性变差。图13表明,弹丸在轴方向的速度最低接近2 m/s,与卡膛速度要求的3 m/s相差较大。
表6所示为由(23)式计算的不同输弹角下的弹丸响应均方差。对比表6中的数据可以发现:随着输弹角的增大,响应的均方差几乎成倍递增;在给定的参数不确定性条件下,轴方向的位移均方差明显大于轴方向,最大可达62 mm;偏角均方差相差无几,均不超过0.08°,卡膛速度均方差最大可达0.4 m/s。
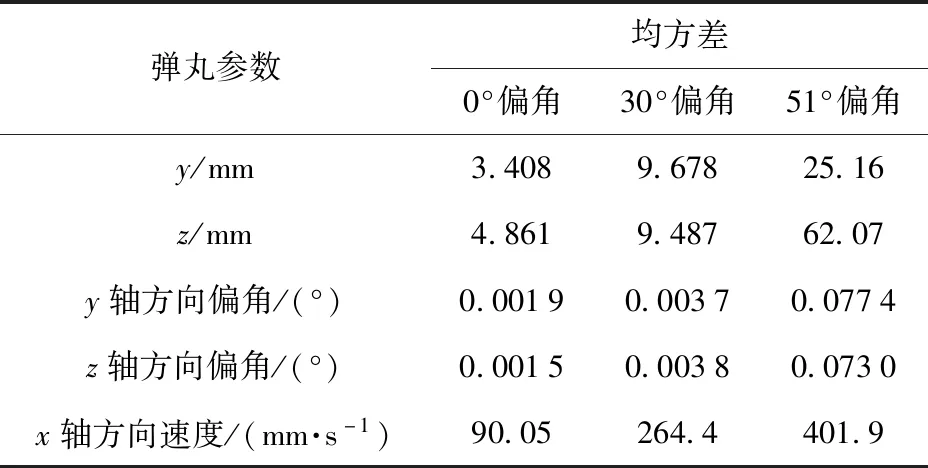
表6 不同工况下的响应散布Tab.6 Dispersion of response under different working conditions
考虑到系统参数的误差几乎不变,为减小弹丸响应的波动,提高卡膛一致性,避免卡膛失败,需要进一步减小输入载荷的误差。
4 结论
本文通过分析某火炮输弹机的结构与原理,建立了输弹机ADAMS仿真模型,基于概率密度演化理论推导了输弹过程概率密度演化方程,并通过有限差分法对其进行求解;分析了不同工况下参数不确定性对输弹响应的影响。得到如下主要结论:
1)通过仿真结果与试验结果的对比,验证了该火炮输弹机动力学仿真模型的准确性。
2)在相同参数条件下,通过PDEM与MC方法的对比,验证了本文方法对涉及高维不确定性参数的输弹过程不确定性分析的适用性。
3)基于不同输弹角的载荷条件拟合弹丸响应的概率密度函数,输弹角越大,弹丸响应的波动越明显,卡膛一致性越差。
4)在本文给定的参数不确定性条件下,输弹结束时弹丸的位移均方差最大可达60 mm,卡膛速度均方差最大可达0.4 m/s。
