飞行器结构布局与尺寸混合优化方法
2022-07-04胡嘉欣芮姝高瑞朝苟建军龚春林
胡嘉欣,芮姝,高瑞朝,苟建军,龚春林,*
1. 西北工业大学 航天学院,陕西省空天飞行器设计重点实验室,西安 710072
2. 北京空天技术研究所,北京 100074
轻量化是飞行器结构设计的重要目标,其本质是实现材料的高效利用,而结构优化技术是实现这一目标的主要手段,根据设计变量的类型,一般分为3个层面:拓扑优化、形状优化、尺寸优化。随着优化技术的发展,优化工具逐渐融入了产品的整个设计流程,对于飞行器设计,一般在初步设计阶段通过拓扑优化技术确定其布局形式,在详细设计阶段通过尺寸和形状优化技术获得更合理的结构形式。
然而,飞行器布局和尺寸的优化设计之间存在较强的相关性,拓扑设计需要考虑结构部件的承载能力,而这正是由部件的尺寸所决定的,因此有必要对二者的混合优化问题展开研究。
针对包含布局与尺寸设计变量的混合优化问题,工程上主要有分级优化策略、整体求解方法2种处理方法。分级优化策略将2种变量分离求解,在布局优化设计的基础上完成位置和尺寸优化,但对于2种变量的耦合关系考虑不足,会导致结构陷入局部最优,精度较低;整体求解方法可以得到优化问题的全局最优解,但在处理多种变量时,不易收敛且耗时较多。
Stanford研究了气动弹性约束下翼盒的形状、尺寸与拓扑优化,使用了一种两级嵌套优化策略,对连续变量使用基于梯度的优化方法,对离散的拓扑变量使用贝叶斯填充方法,并通过代理模型提升计算效率。Qin等以混合动力履带车辆为对象,提出了一种拓扑、能量管理和参数匹配相结合的协同优化方法,并使用了递进迭代方法进行求解,其研究对象与传统结构优化不同,但均包含了拓扑和尺寸设计的概念。An和Huang针对框架式结构的拓扑和尺寸优化问题,提出了一种两级多点逼近策略,首先采用遗传算法对离散变量进行优化,在计算适应度时,使用对偶法求解二级近似问题,完成对梁的截面优化。
Savsani等针对桁架结构在静力和动力约束下的拓扑和尺寸同时优化问题,对比了4类元启发式算法的优化结果,并提出了一种基于随机变异的改进元启发式算法。Assimi和Jamali提出了一种混合遗传规划算法,用于解决包含动静约束的拓扑和尺寸优化问题,并引入了Nelder-Mead局部搜索算子,以提高收敛速度。Fernandez等利用水平集函数描述结构的形状与拓扑信息,并考虑了材料属性的影响,提出了一种形状、拓扑和材料同时优化方法。
虽然分层优化策略通过将结构优化分解为不同层次的优化问题,降低了问题的复杂程度,但是对布局和尺寸变量间的耦合性考虑不足,导致结构优化的可行域减小,降低了优化效果,且层次达到三级或以上时,计算量也会大幅提升。因此,建立结构布局与尺寸混合优化方法对进一步提升结构优化效果、提高结构承载效率具有重要意义。
本文提出一种结构布局与尺寸混合优化方法,在基结构法(Ground Structure Method)的基础上引入尺寸变量,选用遗传算法进行寻优,并在优化过程中使用神经网络代理模型以提高混合优化的效率。
1 结构布局与尺寸混合优化模型
结构布局和尺寸对结构质量有着重要的影响,且二者在结构设计与优化中存在一定的相关性,因此将二者单独进行优化显然是不合适的,而目前常用的分层优化策略对二者的耦合关系考虑得不够充分,可能导致优化的可行域减小。为提升结构优化效果,本文建立结构布局与尺寸混合优化模型,综合考虑二者之间的耦合关系对优化结果的影响。
拓扑优化是确定结构布局的主要优化手段,主要分为连续体拓扑优化和离散体拓扑优化。连续体拓扑优化结果通常为边界不光滑的结构,很难与尺寸优化结合;而离散体拓扑优化以结构部件为基本单元,如Herbert等于1964年提出的基结构法,主要应用于桁架结构的优化设计,其优化结果更接近工程应用方案,且容易与尺寸优化相结合。
基结构法在飞行器设计领域有较多应用,Sleesongsom和Wang等基于部分拓扑优化方法,分别以变体飞行器机翼的方形翼盒和蒙皮骨架式机翼为研究对象,完成了结构布局的优化。
本文按照基结构法的思路,用0-1型离散变量表示结构部件是否保留,变量值为0时表示相应的部件被删除,1则表示部件被保留;用连续的实数变量表示结构部件的尺寸,则结构布局与尺寸的混合优化数学模型可以表示为
find,
min(,)
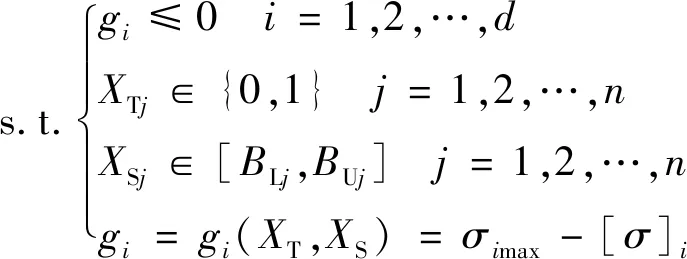
(1)
式中:为结构部件的拓扑变量,取值为0或1;为结构部件的尺寸变量,维数与相同;(,)为飞行器结构质量;为结构优化的约束条件;为当前模型中有效的部件数量;为基结构模型中总的部件数量;、分别为结构尺寸变量的下界和上界。本文只考虑结构强度约束条件,即=max-[],max为第个部件上的最大米塞斯应力,[]为其许用应力。
式(1)中优化变量有拓扑变量和尺寸变量两部分,取值为0或1,为连续的实数变量,因此,该优化问题为混合优化问题。另外,式(1)中与同时作为优化变量,导致优化问题的维数较大,形成了高维优化问题。
对于该混合优化问题,优化变量的类型包括连续变量和离散变量,难点在于离散变量的处理。离散变量的优化问题属于组合优化问题,当优化变量过多时,会出现NP(Non-deterministic Polynomial)难题,导致问题无法求解。目前解决混合优化问题的算法主要有圆整法、分支定界法、启发类的算法(如遗传算法、模拟退火算法)等。其中遗传算法原理相对简单、易于针对具体的问题做出相应的改进,因此,本文采用遗传算法求解式(1) 的混合优化问题。为提高优化效率,本文还使用神经网络代理模型,最终建立相对高效的结构布局与尺寸混合优化流程。
2 基于遗传算法的高效混合优化方法
2.1 针对混合优化问题的遗传算法改进
遗传算法一般包括5大关键因素:① 染色体编码;② 种群初始化;③ 适应度函数设计;④ 遗传算子操作;⑤ 控制参数设定。本文根据混合优化问题的特点,对染色体编码和遗传算子操作方式进行改进,并完成原问题的去约束化和适应度函数的设计。
2.1.1 染色体编码方式改进
将染色体分为拓扑变量部分和尺寸变量部分,使用二进制数串表示,见式(2),并且拓扑变量与尺寸变量一一对应,即T、S分别为第个结构部件的拓扑取值、尺寸取值。拓扑变量的取值为0或1,在计算目标函数和约束函数时,不必对拓扑变量部分进行相应的解码;而尺寸变量部分则需要对相应的二进制数串进行解码,获得实际尺寸数值。
,,…,T|,,…,S
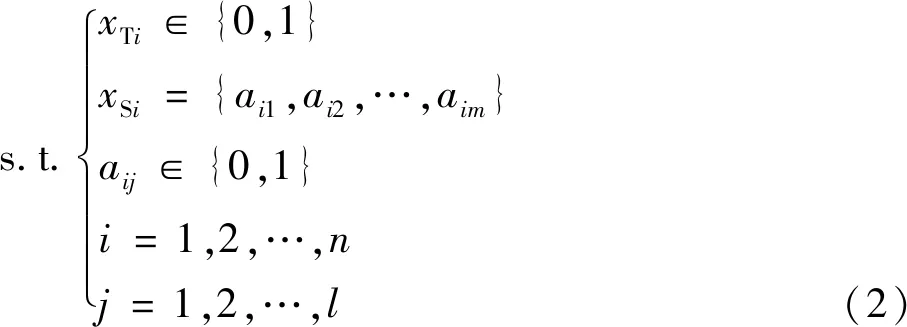
式中:T为结构部件的拓扑变量,取值为0或1;S为结构部件的尺寸,其形式为组成的二进制数串;为结构部件数;为S的编码宽度。
陈秀等在使用遗传算法进行混合优化设计时,直接将同一部件所对应的离散和连续变量配对编码,并未改变其表达形式。而本文则将连续变量转换为了二进制数串,统一了表达形式,提升了后续的遗传算子操作效率。在遗传算法的优化过程中,自然二进制码在连续整数间可能出现较大的Hamming距离,对于高精度问题表现不稳定,局部搜索能力差。格雷码对二进制编码进行了改进,使连续的2个整数所对应的编码值之间只有一个码位不同,方便交叉和变异,提升了算法的局部搜索能力,因此本文采用格雷码对染色体进行编码。
2.1.2 遗传算子操作方式改进
遗传算法的操作算子主要有选择、杂交、变异,在优化过程中通过对个体染色体的改变,淘汰种群中的劣势个体,保留优良的基因。
本文设计的混合优化流程中,染色体分为拓扑变量和尺寸变量两部分,为避免两者相互干扰,对染色体的拓扑变量和尺寸变量部分采用单点杂交(Single-point Crossover)方式。具体的杂交过程如图1所示。
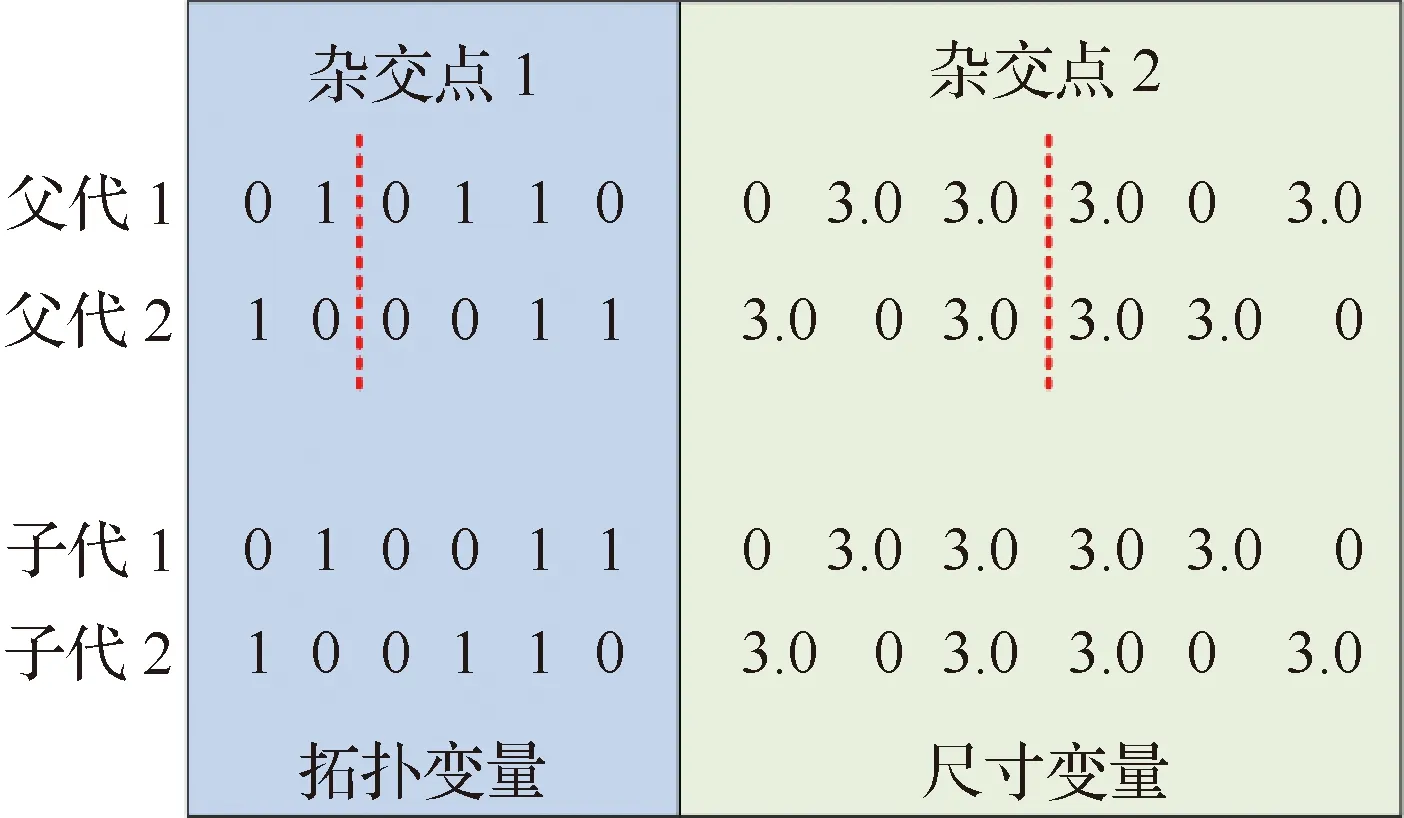
图1 杂交算子操作过程Fig.1 Genetic crossover operator
上述杂交算子不仅实现了杂交算子重新生成子代染色体的过程,还避免了在运用交叉算子过程中破坏染色体的构成。
而遗传算法中变异算子和选择算子与染色体的构成无关,因此选择常用的基本位变异法(Simple Mutation)和随机遍历采样法(Stochastic Universal Sampling)。
2.1.3 基于罚函数法的去约束化设计
结构布局与尺寸混合优化问题为约束优化问题,用遗传算法处理前需要去约束化,一般可使用外罚函数法,对于式(1)的混合优化问题,可构造含惩罚项的增广目标函数
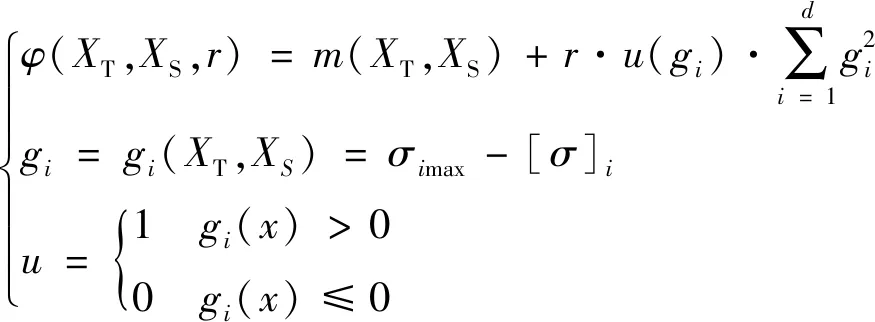
(3)
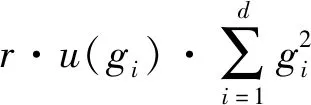
为了减少约束的计算次数,提高遗传算法的优化效率,将式(3)改写为

(4)
在计算(,)时,需要根据、的取值建立相应结构的有限元模型,例如部件数为6时,解码后的染色体如图2所示。
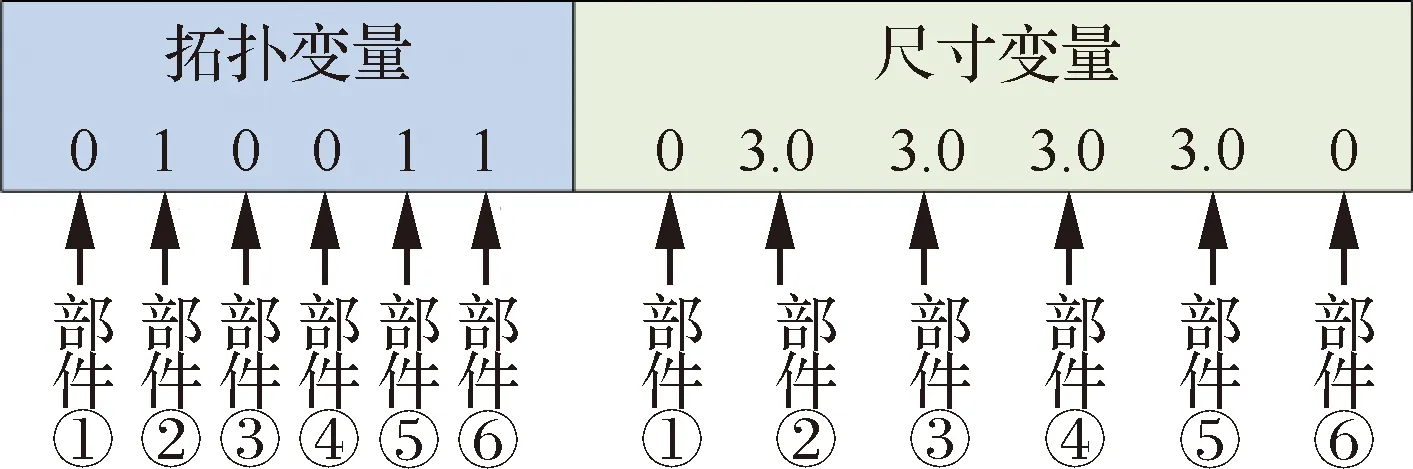
图2 染色体解码Fig.2 Genetic decoding
根据图2,拓扑变量与尺寸变量的相应关系,可以分为下列4种情况:
拓扑变量取1,尺寸变量不为0的情况,如部件 ②。
拓扑变量取0,尺寸变量不为0的情况,如部件 ③。
拓扑变量取1,尺寸变量为0的情况,如部件 ⑥。
拓扑变量取0,尺寸变量为0的情况,如部件 ①。
情况2、3所对应的结构布局是不存在的,因此需要将情况2、3所对应的结构部件从基结构中移除,并建立相应的有限元模型,计算时直接将相应的拓扑变量和尺寸变量相乘即可。
2.1.4 适应度函数设计
适应度函数是评价种群个体的主要指标,将直接影响个体被选择的概率和收敛速度。辛馡和朱鳌鑫对适应度函数进行了研究,提出了5种选取原则:① 规范性;② 单值、连续;③ 合理性;④ 计算量;⑤ 通用性。适应度函数可通过将目标函数映射成求最大值的形式获得,最简单的形式即为目标函数本身(求最大值问题)或其相反数(求最小值问题),也可使用比例化等方法,构造较为复杂的映射。
由于本文的优化目标是最小化结构质量,则适应度函数应是与目标负相关的形式。使用基于排序的适应度分配,相比于直接对目标函数进行缩放映射,排序的方法可通过选择压力(Selective Pressure, SP)参数控制种群多样性,避免“超级个体”导致种群早熟的问题。
本文基于Whitley和Chipperfield等的相关研究,对计算得到的目标函数值进行降序排列,获得个体的排序位置后,构造值域为[0, 2]的适应度函数
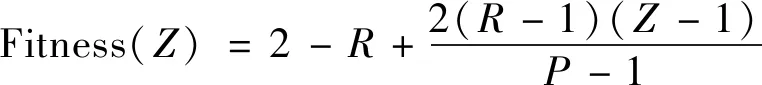
(5)
式中:为选择压力,取值范围为[1, 2];为降序排列下个体的位置序号;为种群内个体数。其中,= 1时选择压力最小,每个个体适应度均为1;= 2时选择压力最大,最优个体适应度为2,最差个体适应度为0。
该适应度函数显然满足辛馡和朱鳌鑫提出的选择原则前3条,此外仅进行排序操作,没有复杂的缩放映射,计算量较少,并具有通用性。
2.2 代理模型在优化流程中的应用
结构布局与尺寸混合优化问题十分复杂且求解非常耗时,对于高维问题更是难以求解,在工程应用中,常使用代理模型技术进行简化。目前,应用最为广泛的代理模型为多项式响应面模型、Kriging模型和神经网络模型等。Adeli和Yeh率先将神经网络近似技术应用到结构设计领域中,为结构设计提供了一种新的智能分析方法。王伟、周丹发等分别使用神经网络模型和响应面模型完成了机翼结构的优化设计,在提高求解效率的同时获得了较好的优化结果。
2.2.1 插值径向基神经网络代理模型
本文利用代理模型预先评估种群个体的优劣,删除一定比例的劣势种群个体以减少种群规模,之后采用精确模型计算剩余优势种群个体的适应度,以减少精确模型的计算次数,提高优化效率。
神经网络代理模型对真实模型的变量维数不太敏感,对于高维优化问题的近似,具有精度较高、计算速度较快的优点。因此,本文采用插值型径向基神经网络,对结构布局与尺寸优化问题进行近似模拟。
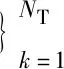
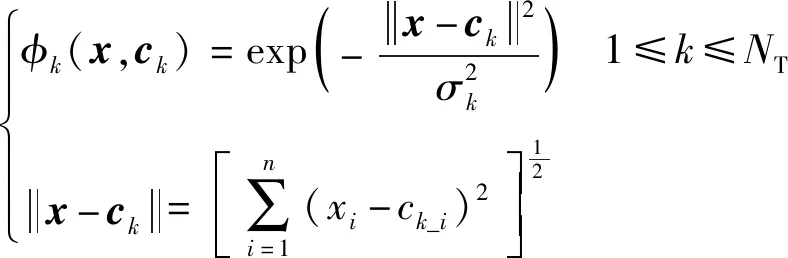
(6)
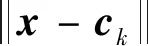
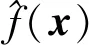
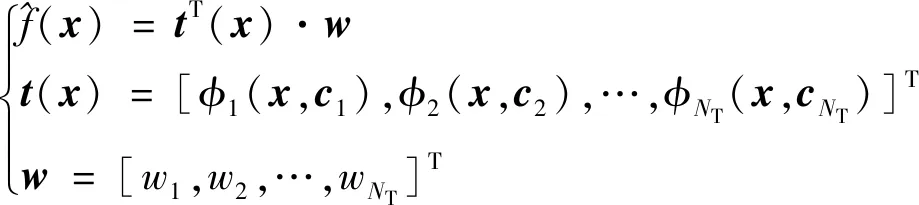
(7)
对于给定的个样本点,插值径向基神经网络模型即表示为
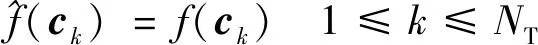
(8)
将式(7)和式(8)联立,并写成如式(9)的矩阵形式:
·=[(),(),…,()]
(9)
式中:
=
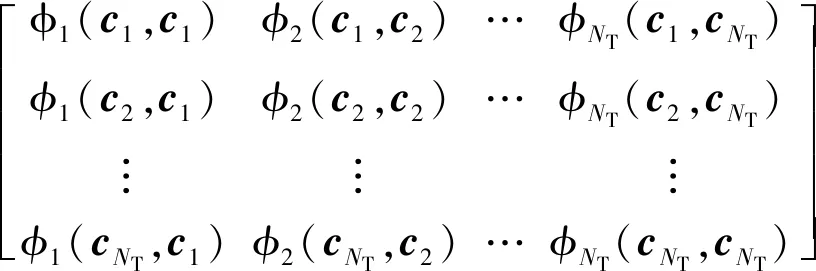
(10)
对于一组给定的形状参数(1≤≤),式(9)为一个线性方程组。若神经元的径向基函数中心点互不相同,则系数矩阵正定可逆,权重系数向量可由式(9)求得。
2.2.2 种群规模的缩减
采用神经网络代理模型代替真实模型计算子代种群的适应度函数,并以近似适应度函数预先评估种群个体的优劣,淘汰适应度函数较差的个体,以达到缩减种群规模的目的。
假定父代种群和子代种群分别为
={,,…,}
(11)
={,,…,}
(12)
式中:为父代个体;为子代个体;为每代种群的个体数。
为了快速计算子代个体的适应度函数,本文先通过试验设计产生初始样本点,并利用神经网络建立代理模型:
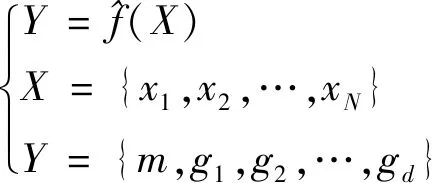
(13)
式中:为优化变量;为种群个体近似适应度。
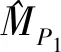
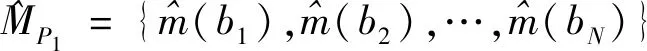
(14)
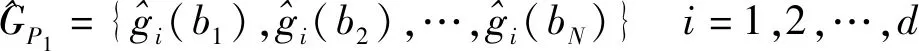
(15)
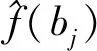
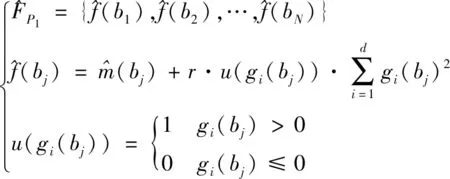
(16)
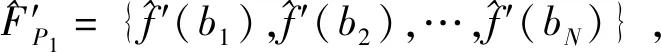
′={,,…,-}
(17)
至此,种群规模的缩减已完成。之后将父代种群与子代种群合并,而原父代个体的精确适应度函数已在上一轮计算过,因此只对′中的个体计算精确的适应度函数值,再通过选择算子选择出个适应度函数较优的个体,形成新的种群,进行后续的操作。
2.3 结构布局与尺寸混合优化流程
结构模型在结构布局与尺寸混合优化过程中不断发生变化,采用固定的结构模型或利用解析方法求解是不现实的。为此,本文提出了如图3所示的结构布局与尺寸混合优化流程。
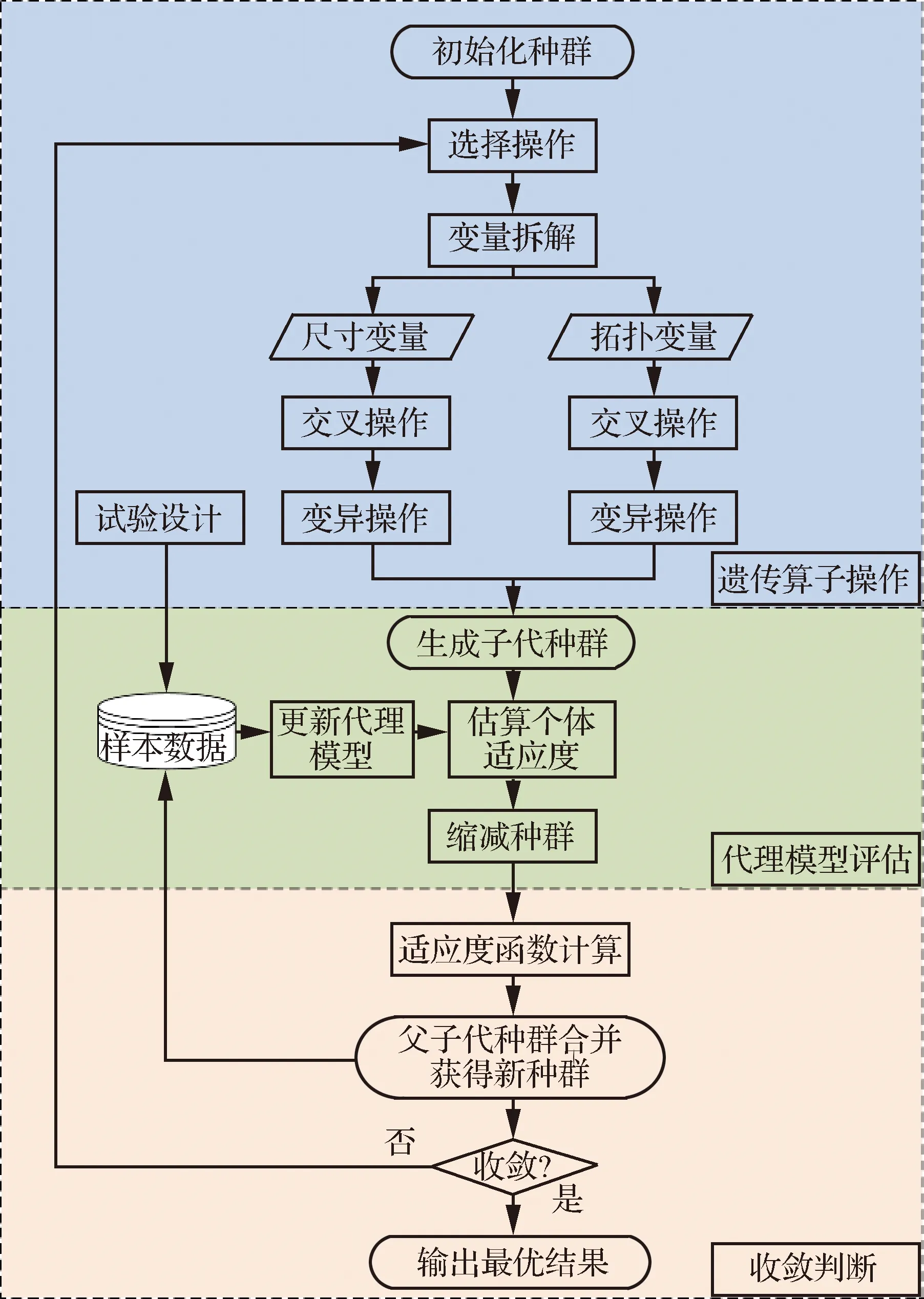
图3 结构布局与尺寸混合优化流程Fig.3 Flow chart of hybrid layout-size optimization
该优化流程主要分为3部分:
1) 遗传算子操作:初始化种群个体,将个体染色体拆分成拓扑变量和尺寸变量,并使用遗传算子分别进行操作,产生子代个体。同时,在遗传算子操作阶段,通过试验设计产生代理模型的初始样本点。
2) 代理模型评估:根据初始样本点建立关于适应度函数的代理模型,以代理模型估算子代个体的近似适应度函数值,“淘汰”适应度较低的个体,缩减种群规模。
3) 收敛判断:使用精确模型计算缩减后的子代种群的适应度函数值,并将之与父代种群按适应度合并形成新一代种群,再判断是否收敛。从新一代种群中选择出适应度函数值近似误差最大的个体,将其加入到样本点数据库后更新代理模型,以获得更为精确的估算结果。
3 算例分析
针对飞行器机翼等相对成熟的结构,基结构的形式容易预先给定,而拓扑优化后的结构布局形式相对简单,易与尺寸优化结合,进行布局与尺寸的混合优化,最终获得更好的优化效果。因此,以某型高超声速飞行器的机翼为研究对象,进行结构布局与尺寸混合优化,具体的建模和仿真分析使用脚本控制Hypermesh和MSC.Nastran软件自动进行。
3.1 机翼的数值及优化模型
图4为机翼的几何模型,采用菱形翼以提高超声速气动性能,由于机翼相对厚度较小,采用平行多腹板式结构布局形式。结构材料为铝合金,其弹性模量=73.1 GPa,泊松比=0.324,密度=2 760 kg/m,强度极限约360 MPa。机翼载荷选择飞行器在30 km、马赫数为4、3°攻角状态下飞行时所受的气动载荷,最大压强在前缘处,约40 kPa,机翼大面积区域压强约20 kPa。
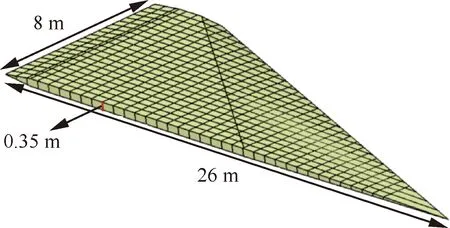
图4 机翼的几何模型Fig.4 Geometry model of wing
机翼基结构布局如图5所示,其平面形状为直角梯形,沿展向布置20根翼肋、沿弦向布置35根翼梁。对于工字梁等复杂截面梁,设计变量较多,而本算例仅用于验证方法,故以最简单的矩形梁为研究对象,其尺寸变量一般包括厚度、高度、长度,针对本文研究的机翼模型,当基结构的分布确定后,梁的高度和厚度由机翼外形所决定,则尺寸变量仅剩下了一维的厚度值。
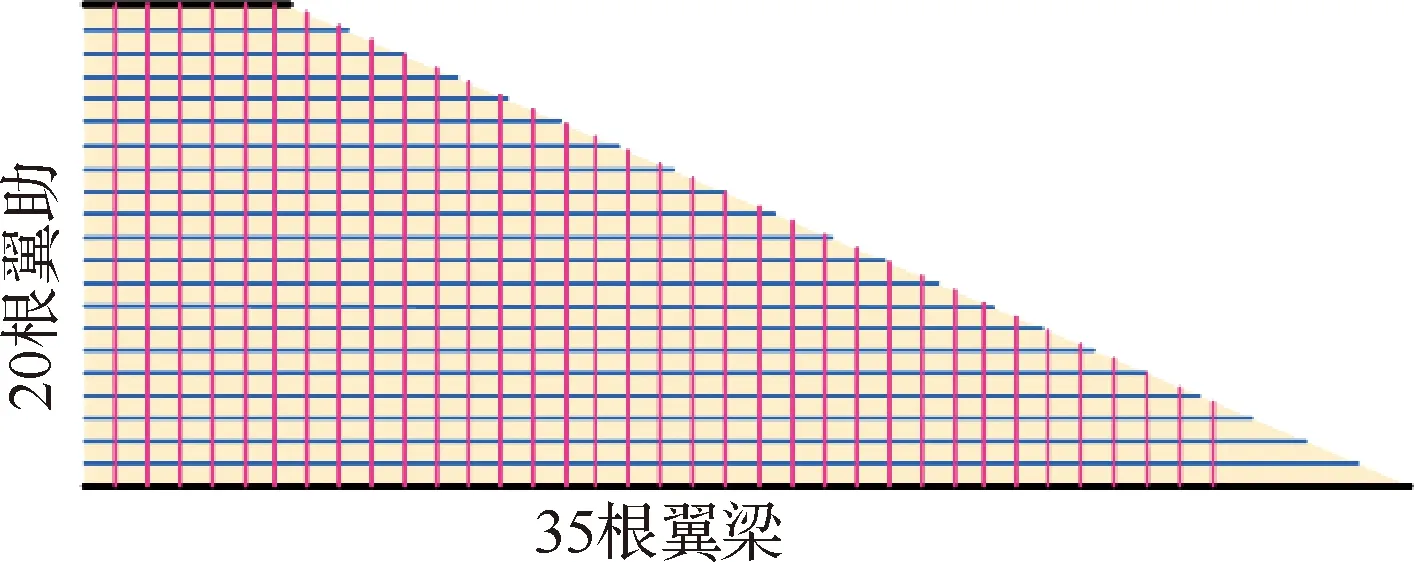
图5 机翼的基结构布局Fig.5 Ground structure of wing
构建有限元模型时,蒙皮、翼梁和翼肋均采用壳单元模拟,单元总数约为2万;蒙皮厚度为3 mm,且与翼肋、翼梁固连;在翼梁的根部位置施加固支边界条件,即忽略机身弹性的影响。
根据机翼的数值模型,建立布局与尺寸混合优化的数学模型:
find,,,
min(,,,)

式中:、为翼肋、翼梁的布局变量,取值为0或1;、分别为翼梁和翼肋的厚度,为结构部件的尺寸变量,mm。
3.2 混合优化方法可行性验证
利用本文所提出的结构布局与尺寸混合优化方法求解式(18),为比较种群规模对优化结果的影响,将遗传算法的种群规模分别设置为30、50、70、90,并将交叉概率和变异概率均设为0.7,进化代数设置为60代。得到机翼结构质量与应力约束随种群代数的变化曲线如图6所示。可以发现,当种群规模大于70时,优化效果几乎不随着种群规模的增大而得到改善。经过30代的进化后,结构质量逐渐收敛,最优值为5.765 t,机翼结构应力约束值在35代后收敛于-0.050 MPa,并且趋于0,表明机翼结构应力接近材料的强度极限,即提高了材料的利用效率。
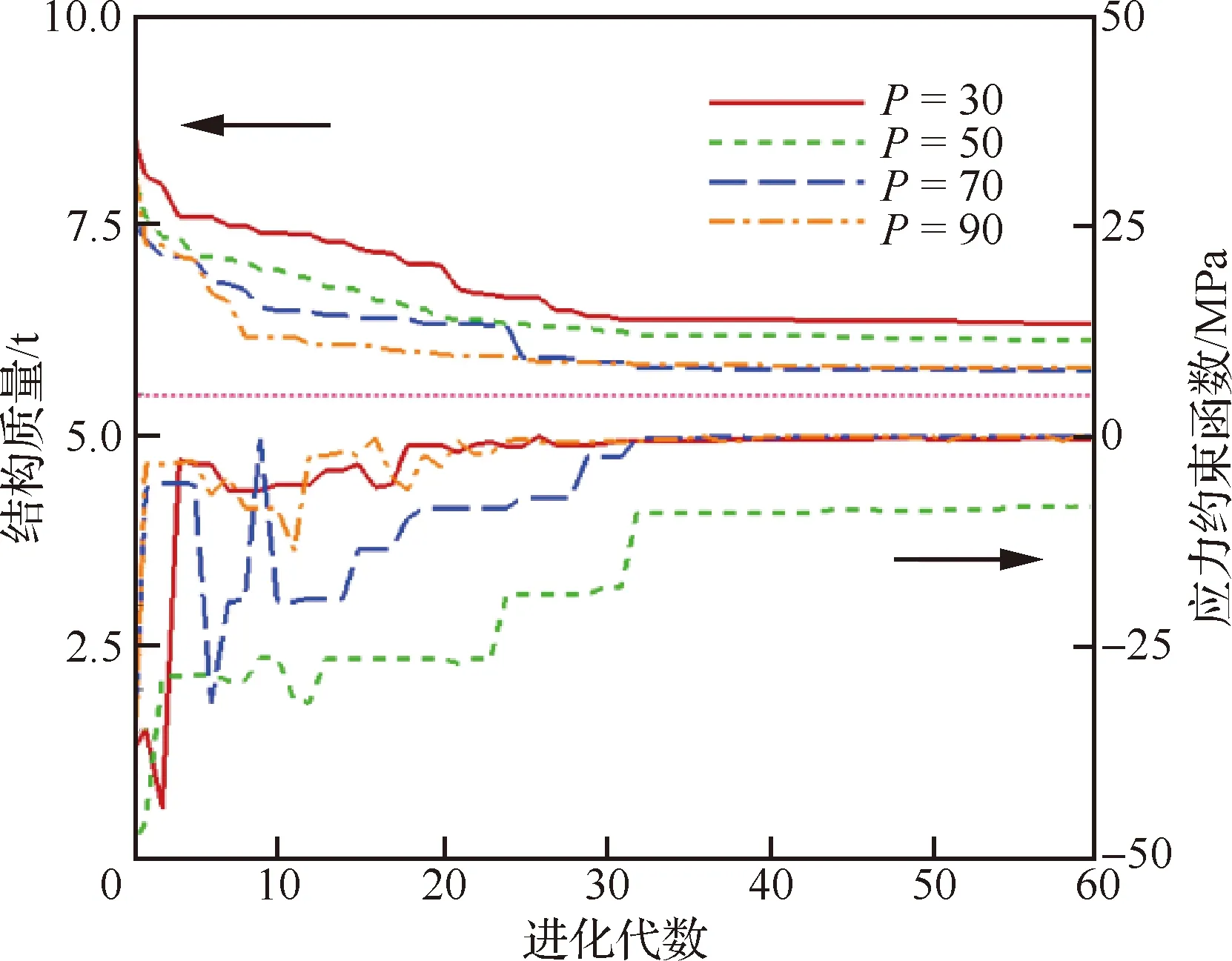
图6 结构质量和应力约束迭代历史Fig.6 Objective and constraint iteration histories
当种群规模=70,进化代数=1, 20, 40, 60时的结构布局如图7所示。对优化前后的机翼结构进行静力分析,结果如图8所示。优化前后,机翼结构最大米塞斯应力分别为94.1、218.0 MPa。从应力的空间分布可以看出,结构优化以减少翼梁或翼肋的数量和改变机翼结构尺寸的方式,提高了机翼结构的整体应力水平,使其逼近结构材料的许用强度,提高了结构的承载效率。
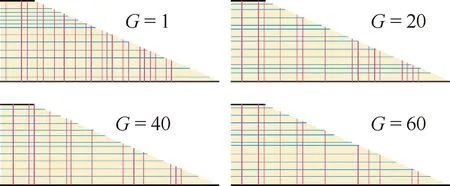
图7 G=1,20,40,60时的结构布局Fig.7 Structural layouts in different generations (G=1,20,40,60)
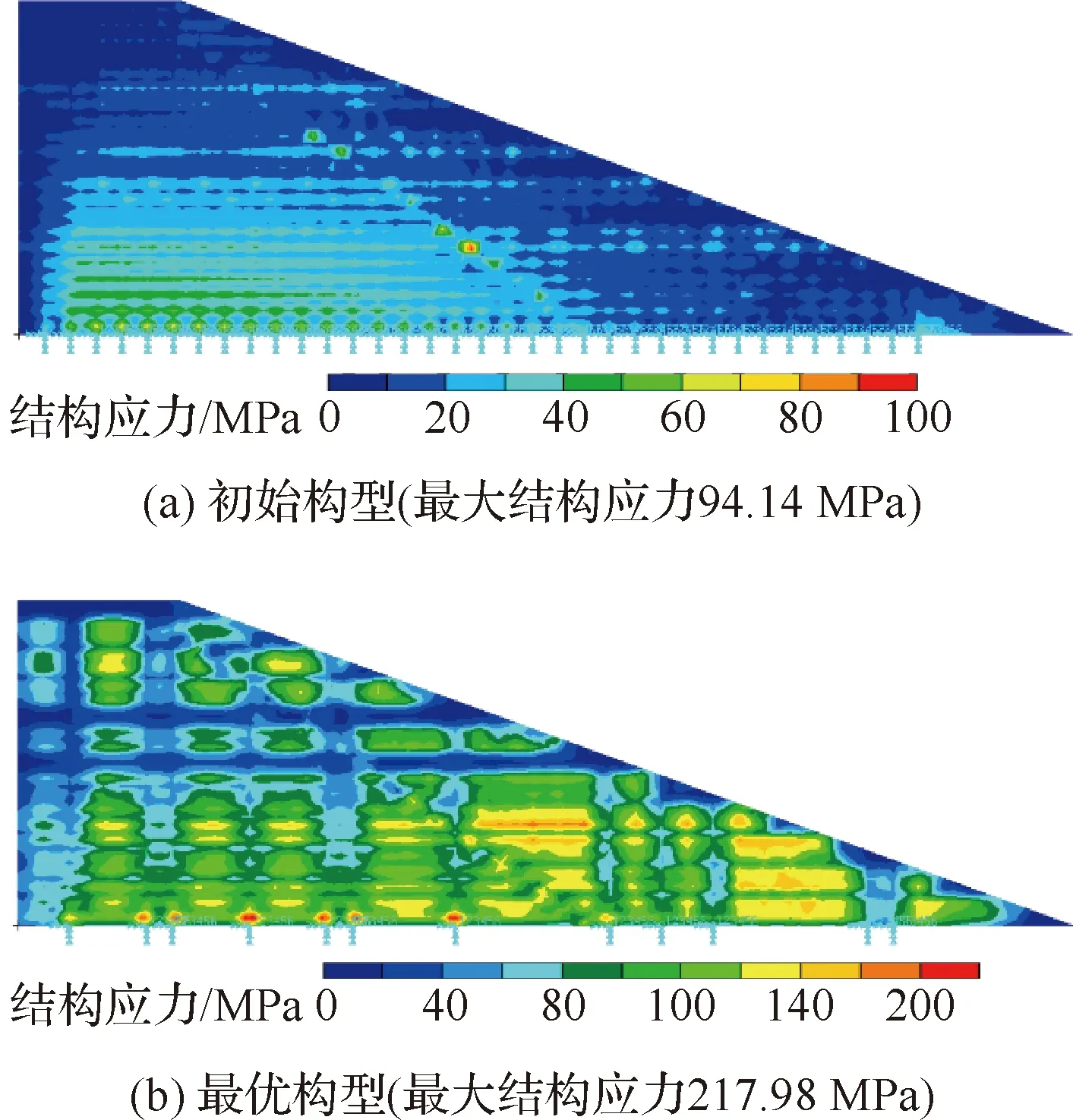
图8 优化前后机翼结构应力分布Fig.8 Stress distributions of initial and optimal wings
结构布局与尺寸的混合优化与单纯的结构布局优化相比,由于考虑了布局与尺寸的耦合,得到的优化结果一般更好。为说明这一点,对上述机翼结构利用基结构法进行布局优化,而机翼翼梁和翼肋的厚度尺寸均取为30 mm,优化结果如图9 所示。
不考虑尺寸参数时,结构布局优化的结构质量为6.637 t,而结构布局与尺寸混合优化的结构质量为5.765 t,相对减少了13.1%。对比图7、图9可以看出,结构尺寸对结构布局具有明显的影响:只进行布局拓扑优化时,机翼翼梁的数目为15根,进行布局与尺寸混合优化时则为12根;此外,2种优化结果中翼梁和翼肋的位置具有较大的差别。由此可以看出尺寸参数对机翼结构布局优化有一定的影响,且布局与尺寸混合优化得到的结果更优。
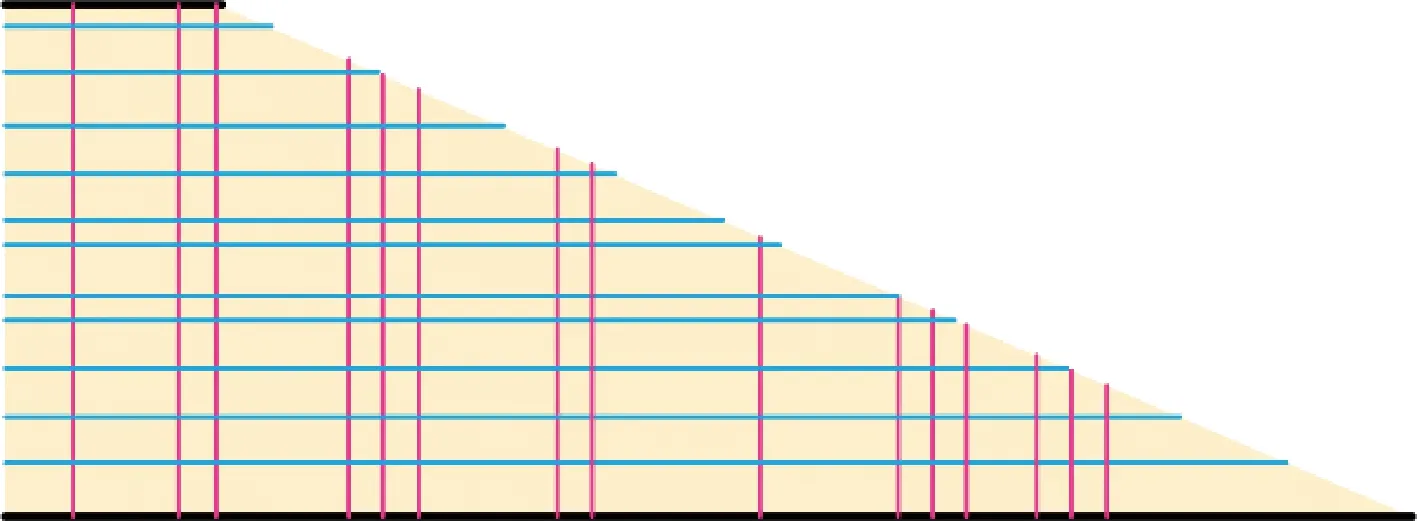
图9 仅使用基结构法的优化结果Fig.9 Optimization result of ground structure method
3.3 代理模型对优化效率的影响
3.2节的分析证明了布局与尺寸混合优化方法的可行性,而本文在2.2节提出了一种使用神经网络代理模型缩减种群规模,提高优化效率的方法,为了研究代理模型的具体影响,构造了3个算例进行对比分析。
算例1即为3.2节中种群规模=70的情况,仅使用真实模型(即有限元模型),作为原始组;算例3根据图3的流程构造,同时使用真实模型和代理模型,作为实验组;算例2仅使用真实模型,计算次数与算例1相同,进化代数与算例3相同,作为对照组,排除种群规模和代数的影响。具体设计参数如表1所示。
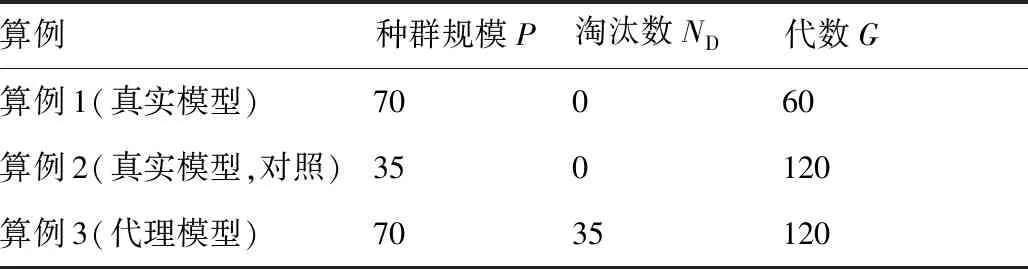
表1 设计参数对比Table 1 Comparison of design parameters
算例3中淘汰数=35指每代使用代理模型估算适应度函数后,删除掉35个表现较差的个体,并与原父代个体合并选择70个个体组成新的种群。
相比于真实模型,代理模型的计算成本很低,在比较优化效率时可以忽略,则计算成本可由(-)来近似表示。具体的优化结果如表2所示,结构质量和应力约束的优化历史如图10所示。
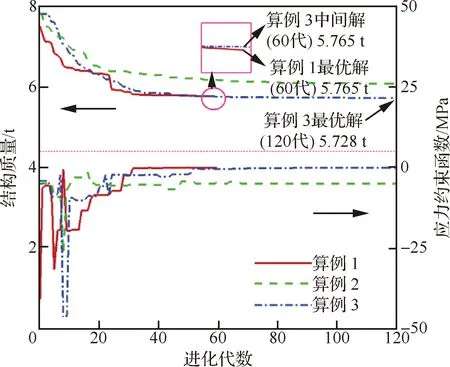
图10 结构质量和应力约束优化历史Fig.10 Objective and constraint optimization histories

表2 优化结果对比Table 2 Comparison of optimization results
可以发现,在计算成本相同的情况下,算例3得到的结果总是最优的。另一方面,算例3中结构质量在第60代就优化到了5.765 t,此时计算成本为2 100次,仅为算例1中结构质量达到5.765 t 时所需计算成本(4 200次)的1/2。
对比算例1、2,在计算成本相同的情况下,算例1种群规模例更大,算例2的进化代数更多,而算例1得到的结果更好,可见,优化结果对种群规模更加敏感;对比算例2、3,也可证明,在优化代数相同的情况下,引入代理模型增加种群规模后,可获得更好的优化效果。因此,通过代理模型增大种群规模是获得更好优化结果的关键。
以上对比分析说明,使用代理模型的优化流程与原始流程相比,在相同的计算成本下,可以得到更优的结果;且在获得相同的优化结果时,代理模型大约节省了50%的计算成本。
4 结 论
针对飞行器轻量化设计中,结构布局与尺寸因相互耦合而导致优化效果较差的问题,本文提出了一种高效的布局与尺寸混合优化方法,在传统基结构优化方法中引入尺寸变量,建立了结构布局与尺寸混合优化模型,并设计了基于遗传算法的求解流程,此外引入了神经网络代理模型以提高计算效率。最终得到了以下结论:
1) 飞行器结构优化设计中,离散型布局变量和连续型尺寸变量可以通过合理设计染色体编码形式来统一描述,进而使用遗传算法完成结构布局变量与尺寸变量的混合优化。
2) 结构的尺寸参数对布局设计有一定影响,进行混合优化可以得到更好的结果,对于本文算例,混合优化方法比单一基结构法更有效,优化结果进一步减重约13%。
3) 代理模型的引入提升了优化效率,在计算成本相同的情况下,包含代理模型的优化流程可以更快地获得良好的优化结果;获得相同优化结果时,代理模型的引入节省了约50%的计算成本。
4) 相比于传统的飞行器结构优化设计方法,本文提出的布局与尺寸混合优化方法设计效率更高,获得的结构质量更轻。
