基于吸引域与二元极值理论的结冰飞机飞行风险量化评估

伍强，徐浩军，裴彬彬,*，魏扬，张杨

1. 空军工程大学 航空工程学院，西安 710038

2. 中国人民解放军 95633部队，成都 611530

在一定气象条件下，大气中的过冷水滴与飞机迎风撞击就有可能导致飞机表面结冰，波音公司统计结果表明，飞机结冰是诱发飞行失控(Loss of Control, LOC)严重事故的3大因素之一，飞机结冰问题长期以来一直受到人们的高度关注。2004年11月21日，东方航空公司一架CRJ-200飞机由于停放后除冰不彻底导致起飞过程中坠毁，机上55人全部遇难。2006年6月3日，某型飞机在多次穿越云层后结冰导致飞机失控，机上40人全部遇难。因此，有必要深入研究结冰条件下的飞机飞行风险，探索结冰对飞机飞行安全的威胁程度，从而制定合理的结冰风险规避策略。

研究结冰飞行风险问题必然涉及到飞行风险评估方法，传统的飞行风险评估方法以定性分析为主，定量分析也仅依据静态安全性指标。Mohaghegh等将系统动力学理论、贝叶斯网络、事件图和故障树等理论应用于飞行风险管控中，提出了航空维修系统风险分析方法。Brooker将马尔科夫链、故障树、事件树等方法成功应用于飞行风险评估中。传统的飞行风险分析方法主要针对元部件故障或人为失误等静态因素，无法研究飞机飞行过程中的动态飞行风险，因此国内外已经将研究重点放在运用仿真手段开展复杂外部条件下飞行风险量化评估，de Mendonça等提出了基于飞行模拟仿真的飞机安全性分析方法，并证明了运用飞行模拟开展飞行安全保障工作的必要性。Blum等讨论了基于蒙特卡罗模拟开展飞机安全性分析的可行性。蒙特卡罗法是在已知随机变量分布规律的条件下，依据变量概率分布随机提取变量样本数据。该方法能够有效模拟随机变量的动态变化过程，准确反映随机变量的参数分布规律，解决复杂系统中的随机性问题，适用于提取飞行仿真中随机变量参数样本。飞行安全关键参数极值样本均具有明显的厚尾分布特性，这种分布形式在低频高危风险事件(如金融风险、自然灾害等)中较为常见。武朋玮等基于可达集方法和极值理论对结冰条件下的飞机着陆风险进行了量化评估，其研究对于指导飞行员操纵具有一定的应用参考价值，但是其采用的是一元极值分布模型，没有考虑各个参数之间相关性。多元极值理论与Copula函数模型快速发展，已经成为研究高危低频风险事件的有力研究工具，李哲、魏扬构建了适用于飞行风险量化评估的多元极值Copula模型，其选择的飞行参数主要包括速度、迎角和滚转角，对于飞机的姿态角及相应的角速度之间的相关性没有进行深入的研究。

运用蒙特卡罗方法和极值理论进行复杂条件下飞行风险量化评估的前提和关键是要设定准确的事故发生判定条件。目前的飞行风险判定标准主要针对某一飞行参数是否超过其极限值，由于各飞行参数极限值是依据经验和试飞得到一维数据，没有考虑到各个飞行参数之间具有的强烈相关性，仅仅根据一维极限值作为判断标准开展飞行风险评估，难以全面有效的描述飞行安全特性。而吸引域方法可用于计算非线性系统的吸引域及稳定边界，进而作为飞行风险判定条件进行飞行风险的定量计算。

本文首先建立了典型运输类飞机纵向动力学模型和结冰影响模型，基于吸引域方法得到了不同结冰程度条件下的飞机基于迎角和俯仰角速率参数的二维吸引域及稳定边界。建立了典型的人-机-环系统模型，运用蒙特卡罗仿真方法，以典型的驾驶员操纵——升降舵脉冲作为输入得到了迎角和俯仰角速率等关键参数极值。根据极值理论，建立了适用于飞行风险量化评估的二元极值Copula模型，通过遗传算法辨识模型参数，根据多种拟合优度检验方法确定了最优分布模型，以飞行状态超出稳定边界作为发生飞行事故的判定条件，计算不同结冰严重程度下的风险概率，进而根据结冰风险概率对驾驶员操纵提出指导。本文创新地提出利用吸引域和二元极值理论评估结冰风险，所得风险评估结果对于研究结冰引起的飞行安全和适航性问题具有重要意义。

1 模型建立

1.1 飞机纵向动力学模型

飞机纵向非线性动力学模型可表示为

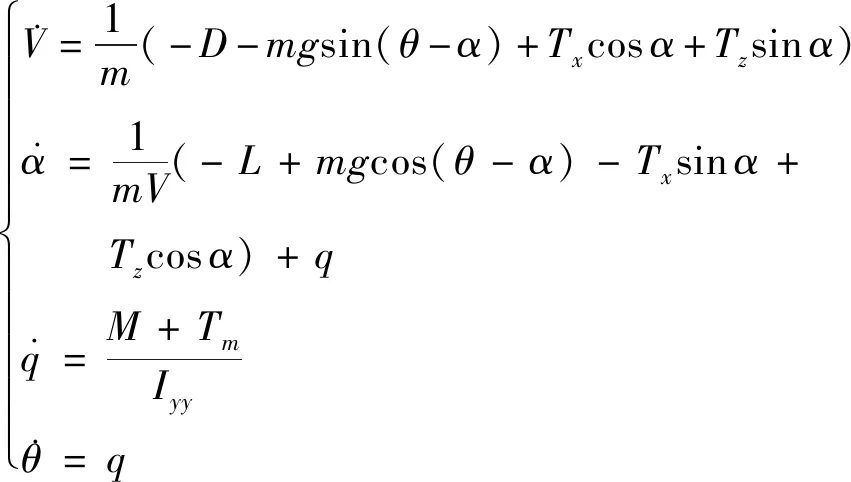
(1)

式中：、、、分别表示空速、迎角、机体俯仰角、俯仰角速率；、分别为推力在机体坐标系、轴上的投影；是由推力产生的俯仰力矩；表示飞机的转动惯量；、、分别表示飞机受到的升力、阻力与俯仰力矩，其计算方式为

(2)

1.2 结冰影响模型

由于开展结冰飞行试验难度大、成本高，本文通过建立结冰影响模型来分析结冰后气动参数的变化。Hui等利用最大似然法获取飞机结冰前后的气动参数，初步建立了结冰外界环境无量纲参数与退化系数相关的结冰影响模型， Lampton与Valasek提出了一种基于试飞数据定义每个气动参数对应的退化因子的简化方法，进而对不同结冰严重程度及结冰分布的动力学响应进行分析；此外，他们还研究了非对称结冰影响模型，用于分析除冰系统单侧故障时的动力学特性，当前常用的是Bragg等提出的结冰参量影响模型，模型可表示为

=(1+)

(3)

式中：与分别表示任意结冰前后飞机的性能、稳定性与控制参数或其导数；表示结冰对飞机气动参数的影响参数，它与飞机自身尺寸、飞行状态或与飞机受结冰影响的敏感性相关；为飞机结冰程度参数，只与气象条件有关。

1.3 飞机本体模型

飞机本体非线性动力学模型可表示为

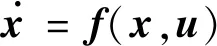
(4)

式中：为状态向量，包含飞行速度、迎角、侧滑角、四元数、俯仰角速率、滚转角速率、偏航角速率和空间位置参数，即

=[,,,,,,,,,,,,]

(5)

为控制向量，包括油门偏度指令、升降舵偏度指令、副翼偏度指令和方向舵偏度指令，即

=[,,,]

(6)

运用四元数法构建飞机动力学模型具体过程见附录A。

1.4 驾驶员操纵模型

进行蒙特卡罗仿真时，需要将驾驶员操纵作为输入，考虑到驾驶员操纵的随机性，认为驾驶员的随机性操纵参数服从参数为的瑞利分布：

(7)

式中：(-)为单位阶跃函数;为操纵量初始值。

2 非线性动力学系统吸引域分析

2.1 基于平方和理论的多项式非线性系统吸引域及稳定边界估计

考虑多项式非线性自治动力学系统：

(8)

式中：()为状态向量。

假定=是系统的局部渐近稳定平衡点，那么平衡点附近的吸引域(Region of Attraction)定义为

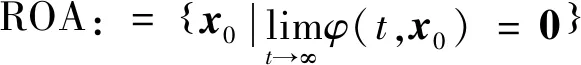
(9)

式中：(,)为初始状态为时动力学系统的解。所有初始状态位于吸引域内的点最终都将收敛于平衡点。

若存在一个连续可微的函数：→使得

1)()=0且∀≠,()>0。

2):={∈|()≤}有界。

3)⊂{∈|▽()()<0}∪{}。

则对于所有的∈，方程(1)的解存在且满足lim()∈。从而，是方程(1)吸引域的子集。

满足定理1的函数称作李亚普诺夫函数(Lyapunov Function)，而可作为吸引域的一个估计。为最大化，可定义一个可变区域()，在约束∈的条件下最大化。

:={∈|()≤}

(10)

式中：是大于零的值；()为正定多项式。利用代数几何中的Positivstellensatz定理，可将该最优化问题转化成下面的平方和规划(Sum-of-Squares Programming, SOSP)问题：

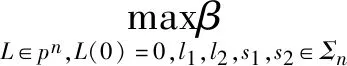
(11)

式中：为所有个变量的多项式集合；表示个变量的平方和多项式集合。结合-迭代算法，可对上述最优化问题进行优化求解，即可估计出多项式非线性动力学系统的吸引域，吸引域的边界也就是该动力学系统的稳定边界：

:={∈|()=}

(12)

在进行估算时，可假定吸引域为一椭球体，对于二维问题，可假设：

()=N=()+()

(13)

式中：=diag(,)为形状函数。

利用SOS理论对非线性动力学系统吸引域求解的前提是建立动力学系统的多项式模型。为此，首先要在合理的区间范围内将飞行动力学模型转化为多项式模型，然后在此基础上计算飞机在平衡点附近的稳定域。

非线性动力学系统吸引域的计算过程如下：

利用多项式拟合对每一项气动系数、推力特性、状态变量的逆等建立起相应的多项式模型。

将建立起的各多项式模型代入常规动力学模型中，进而推导出飞机动力学模型的多项式表达式。

为便于计算，通过坐标变换将飞机多项式动力学模型的平衡点移动到原点，并去除不必要的项(系数很小或阶数很高)。

基于SOS理论计算出飞机在原点附近的吸引域。

通过坐标反变换将计算出来的吸引域映射到以原平衡点为中心点的区域，该区域即为飞机状态参数的局部渐近稳定区域,即吸引域。

2.2 飞机纵向多项式动力学模型

进行非线性动力学系统吸引域的计算时，首先需要将常规的飞机非线性动力学模型转化为多项式模型。常规的飞机非线性动力学模型表达式中存在着一些非多项式项，主要包括三角函数项、气动力(矩)系数、速度的逆等。在转换为多项式的过程中，多项式的阶数越高，计算精度也就越高，但同时会带来计算量的增加。因此，需要确立合适的多项式阶数。

对于三角函数的转化可采用泰勒级数展开方法，一般展开至三阶即可。在[(45°,45°]的范围内，sin函数与cos函数的误差都比较小，例如30°时，sin函数与cos函数估算值与实际值之间的误差分别为0.065%与0.35%

常规的飞机非线性动力学模型(如式(1)所示)中含速度的逆，即1/。由于理想情况下，动力学系统的多项式模型不应该含有指数为负的项,为此，在合适的速度区间上用二次多项式来拟合速度的逆，从而得到近似的多项式表达式：

=++

(14)

式中：、、为待定常系数，通过曲线拟合来计算。飞机结冰一般在速度较低的情形下发生，考虑到飞机的最小平飞速度限制，在对速度进行拟合时，拟合区间选定为80～150 m/s，在此区间内，拟合误差均在10数量级，例如当速度为100 m/s 时，误差为0.791%，拟合结果为

=7153 1×10-

2447 4×10+0027 4

(15)

在飞机动力学模型中，空气动力(矩)以及发动机的推力与飞机状态参数、操纵参数有关，一般用插值算法对气动参数表进行计算。本文以通用运输类模型(Generic Transport Model, GTM)风洞试验得出的数据为基准，经过相似准则变换后形成TCM(Transport Class Model)模型进行分析计算。为便于开展吸引域分析，本文基于最小二乘拟合算法来计算气动参数(包括升力系数、阻力系数、俯仰力矩系数)的多项式表达式。这里以背景飞机在干净构型下的升力系数为例进行说明，升力系数可分解为

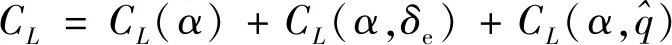
(16)

式中：()是只与迎角有关的基本气动参数，选用一元四阶多项式进行拟合，得到其多项式表达形式为

()=-0791 6+4388 6-7790 9+

5137 2+0068 9

(17)

(,)是与迎角和升降舵操纵量有关的项，这里选定用二元二阶多项式进行拟合，得到其多项式表达形式为

0034 6+0454 7+0002 5

(18)

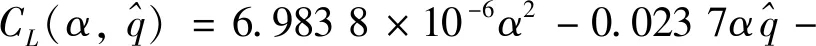
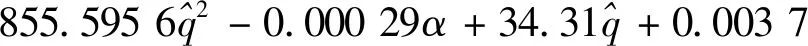
(19)

升力系数各项的多项式拟合结果与真实值之间的对比如图1所示。

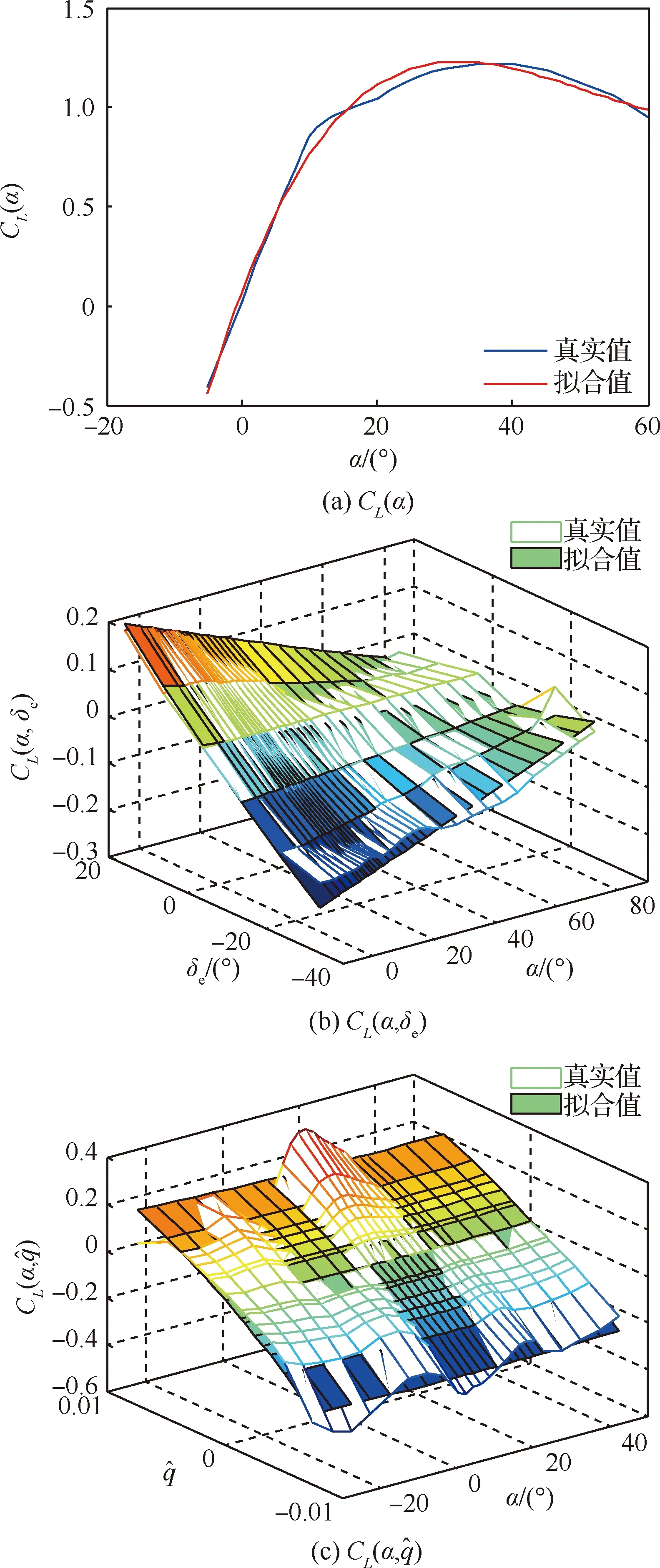
图1 升力系数各项拟合值与真实值之间的对比Fig.1 Comparison between fitted and true values of lift coefficient

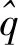
10-2316 4×10-

0000 6+5587 4×10+

0000 9+0080 5-0022 5+

0022 9-0097 7-4415 1-

0016 7+2464 7+0003 7

(20)

将式(17)、式(18)、式(20)代入式(16)便可得到升力系数的多项式表达式。利用同样的方法，可得到阻力系数、俯仰力矩系数的多项式表达式。在进行拟合计算时，非线性动力学模型中各角度均以(°)为单位。同时，需要指出的是，该多项式表达式成立的参数范围需满足飞机气动参数插值表中给出的插值范围限制。对于该型飞机而言，各参数的有效范围为：∈[-10°, 60°],∈[-30, 30](°)/s,∈[-30°, 20°]，∈[80,150] m/s。

在进行飞机稳定性分析时，通常不考虑发动机推力的变化，而是把发动机的推力维持在配平状态，这里发动机的推力采用简化的推力模型进行计算，认为发动机的推力只与油门偏度有关，油门偏度的取值范围为0～100%。根据发动机推力值与油门偏度之间的差值数据，同样可用多项式拟合的方法，得到发动机推力的多项式模型：

(21)

通过上述对常规动力学模型中非线性项的多项式转化，可将常规的飞机纵向非线性动力学模型转化为多项式形式的微分方程组。

2.3 基于SOS理论的吸引域计算

2.3.1 多项式动力学模型简化

飞机纵向扰动有两种典型的模态：长周期模态与短周期模态。飞机受到扰动后，首先是短周期模态参数、的变化较为迅速，一旦发散对飞行安全造成很大影响；长周期模态参数、的变化较为缓慢，在短时间内可视为不变，并且驾驶员具有较长的时间对其进行修正。因此，短周期多项式模型与全量多项式模型在短时间内的动态响应差别不大，其主要的区别在于扰动后飞行轨迹趋于平衡点阶段，短周期模型能很快地趋于平衡点，而全量模型由于其中长周期模态的存在，状态参数趋于平衡点过程中存在着低频小幅震荡，这些差别对于吸引域的计算影响不大。同时考虑到状态变量增多引起的计算量增大的问题，本文在计算过程中将、视为定值(即配平值)，将全量多项式模型简化为只含有短周期模态参数、的多项式短周期模型。

基于上述思想，飞机的初始飞行状态设定为在=2 000 m高度上以=120 m/s的速度做水平直线飞行，多项式动力学模型的平衡点为：=120 m/s，=626°，=0 (°)/s，此时的输入变量为：=2225，=049°。将全量多项式模型中的、、、分别替换为它们各自的配平值，便可得到代表飞机短周期模态的多项式模型。按照吸引域的定义，在进行多项式系统的吸引域估计时，平衡点为零点。为满足这一条件，将模型的平衡点移动至原点，可以通过将、分别替换为+、+来进行计算。同时，为简化计算，可略去系数小于10的项。

最终将常规的飞机非线性动力学模型(式(1))按照上述方法转化得到的多项式短周期动力学模型为

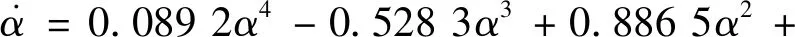
0004 3+0056 5-0537 8+0891 2

(22)

1423 2-0783 5

(23)

需要再次指出的是，上述转化的多项式动力学模型的有效范围同样必须满足2.2节中多项式模型推导过程中的约束条件：对于迎角而言，其有效范围为∈[-10°,45°]，俯仰角速率有效范围为∈[-30,30] (°)/s，升降舵偏角有效范围为∈[-30°,20°]，飞行速度有效范围为∈[80,150] m/s。

2.3.2 吸引域及稳定边界计算

将式(13)中的形状函数定义为：=diag(20°,30(°)/s)，便可得到正定多项式：

()=8207+3647 6

(24)

基于SOS理论，利用-迭代算法，便可得到飞机在原点附近的吸引域：

′={,∈|0603 6-0279 7+

0538 9≤0580 5}

(25)

相应的稳定边界为

′={,∈|0603 6-0279 7+

0538 9=0580 5}

(26)

上述计算吸引域的过程中，需要将平衡点从配平状态点移至坐标原点，所以在获得原点附近的吸引域′后，将吸引域中心平移至原配平状态点，即可得到飞机在配平状态点附近的吸引域：

={,∈|0603 6(-0109 3)-

0279 7(-0109 3)+0538 9≤0580 5}

(27)

吸引域的物理意义为：当飞机受到阵风或其他不利扰动后，只要其状态参数位于吸引域内，飞机就能回到原来的平衡状态。

多项式模型转化过程中拟合函数的误差会导致多项式模型的动态响应与常规的非线性动力学模型的响应存在误差，进而会导致基于SOS理论计算得到的吸引域与飞机实际的稳定域存在一定的出入。为验证多项式模型转化及SOS理论计算吸引域方法的有效性，将背景飞机常规动力学模型中的短周期模态参数在各个初始状态点上的动态响应投影到-相平面上,与所计算出的吸引域进行对比分析，如图2所示。每一条相轨迹始于平面内设定的初始状态点矩阵，红色曲线表示初始状态点最终演化至发散的轨迹，蓝色曲线表示初始状态点最终演化至平衡点的轨,绿色曲线围成的区域为计算出的吸引域。显然，吸引域位于平衡点附近的稳定范围内且占据了稳定范围大部分的面积，始于吸引域内每一个状态点均能回到平衡点，说明采用SOS理论计算得出的稳定边界虽然偏于保守，不能完全包含整个稳定范围，但基本上能够反映出飞机在平衡点附近的稳定范围。

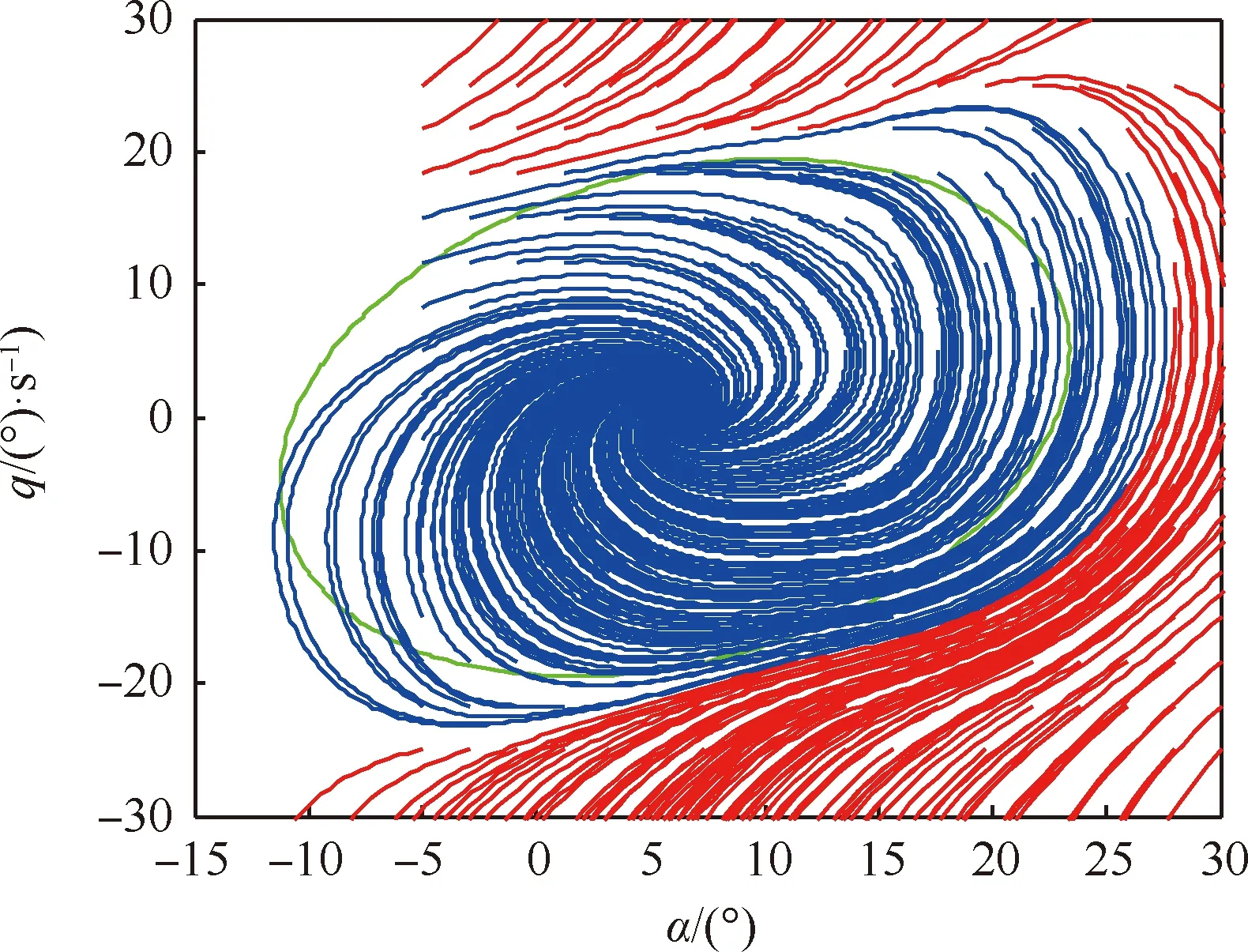
图2 干净外形时α-q的相平面图Fig.2 Phase plane plot of α-q in clean shape

3 基于极值理论的飞行安全关键参数分布模型

3.1 一维极值分布模型

一维极值分布模型能够有效地描述结冰情形下飞行安全关键参数极值样本的概率分布情况和样本数据边际概率分布尾部特征。当前，其他高危低频事件中应用最为广泛的一维极值分布模型是广义极值分布模型(GEV)。GEV模型由Fisher-Tippett定理推导所得，推导过程见附录B。

3.2 一维飞行安全关键参数分布模型

针对飞行安全关键参数具有的厚尾特性，选取能够有效描述尾部分布规律的5种分布模型，分别是极值理论中的极值分布(EV)、广义极值分布(GEV)以及能够描述尾部分布特性的对数正态分布(Logn)、指数分布(Exp)和威布尔分布(Wei)，同时选择正态分布(Norm)用做对比分析。上述模型的分布函数分别为

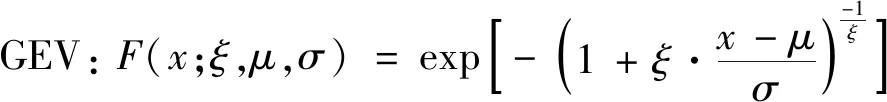
(28)

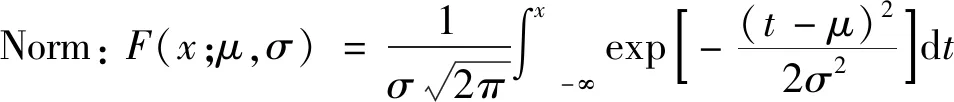
(29)

(30)

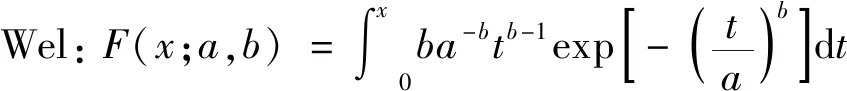
(31)

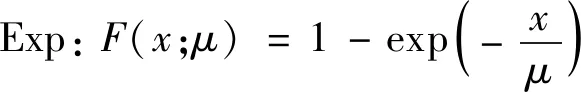
(32)

(33)

在运用蒙特卡罗仿真方法获取迎角及俯仰角速率极值样本(见附录C)的基础上，通过遗传算法辨识上述模型中的未知参数变量，辨识结果如表1所示。

表1 一维极值模型参数辨识结果Table 1 Parameter identification results of one-dimensional extreme value model

首先通过QQ图检验法初步判定6种分布的拟合精度。在已知分布函数的未知参数取值后，可依据原样本极值参数绘制QQ图。从理论角度分析，极值参数的分布函数为(;,,…,)时，QQ图中的图像应近似为一条直线，若图形偏离直线较大，则认为该种形式的分布不满足样本观测值分布特性。上述目标样本分布模型的QQ图如图3所示。

由图3(a)可知，对于迎角极值，GEV分布模型的QQ图最接近于直线，而其他分布模型的QQ图均不同程度的有偏离趋势，其中，Exp和Logn分布模型的偏离程度较低，而Norm、Wei和EV分布模型偏离较为严重。同理，由图3(b)可知，对于俯仰角速率极值，GEV分布模型的线性程度最高。

图3 QQ检验图Fig.3 QQ inspection chart

表2 迎角极值拟合优度检验Table 2 Goodness-of-fit test for extreme angle of attack

表3 俯仰角速率角极值拟合优度检验Table 3 Goodness-of-fit test for extreme pitch rate

3.3 二元飞行安全关键参数Copula模型

通过Sklar定理可以看出，Copula函数能够有效地分析多维联合分布(详见附录D)。常见的二元Copula模型主要有Gumbel Copula模型(Gum)、Frank Copula模型(Frank)、Clayton Copula模型(Clay)及Joe Copula模型(Joe)。上述模型的分布函数分别为

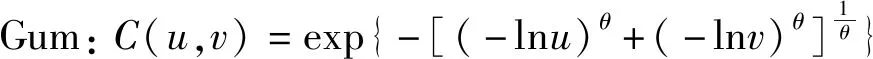
(34)

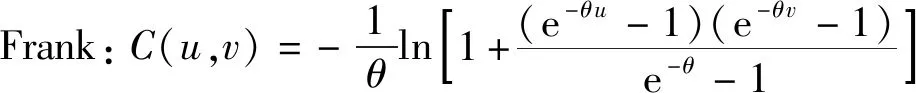
(35)

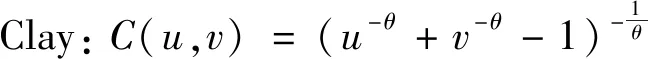
(36)

Joe:(,)=1-[(1-)+(1-)-

(37)

式中：、分别为迎角极值和俯仰角速率极值的边缘分布。

=()

(38)

=()

(39)

相应的概率密度函数(,)可表示为

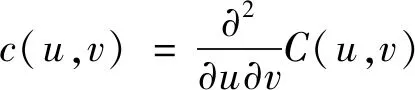
(40)

通过遗传算法辨识上述模型中的未知参数，辨识结果如表4所示。

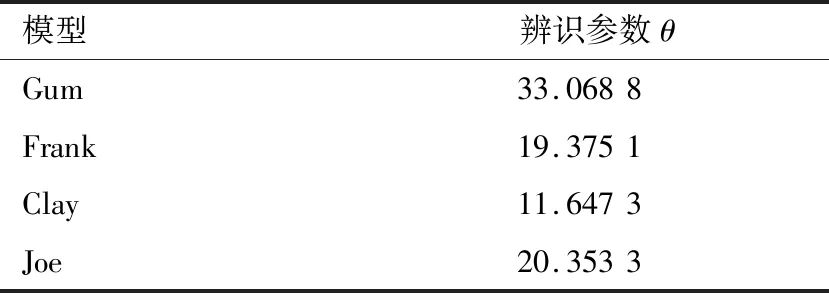
表4 Copula模型参数辨识结果Table 4 Parameter identification results of Copula model

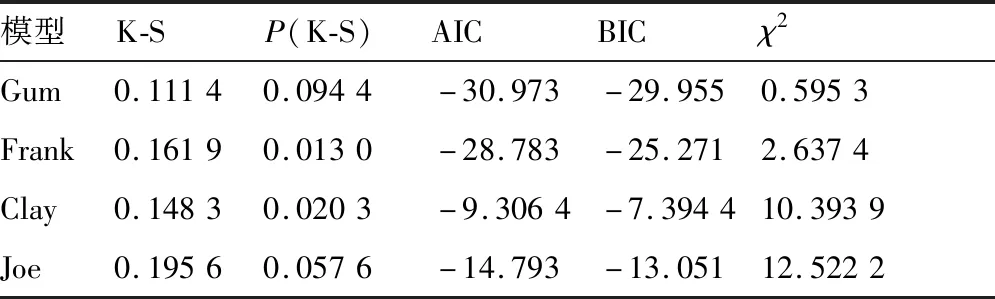
表5 Copula函数拟合优度检验Table 5 Goodness-of-fit test for Copula function

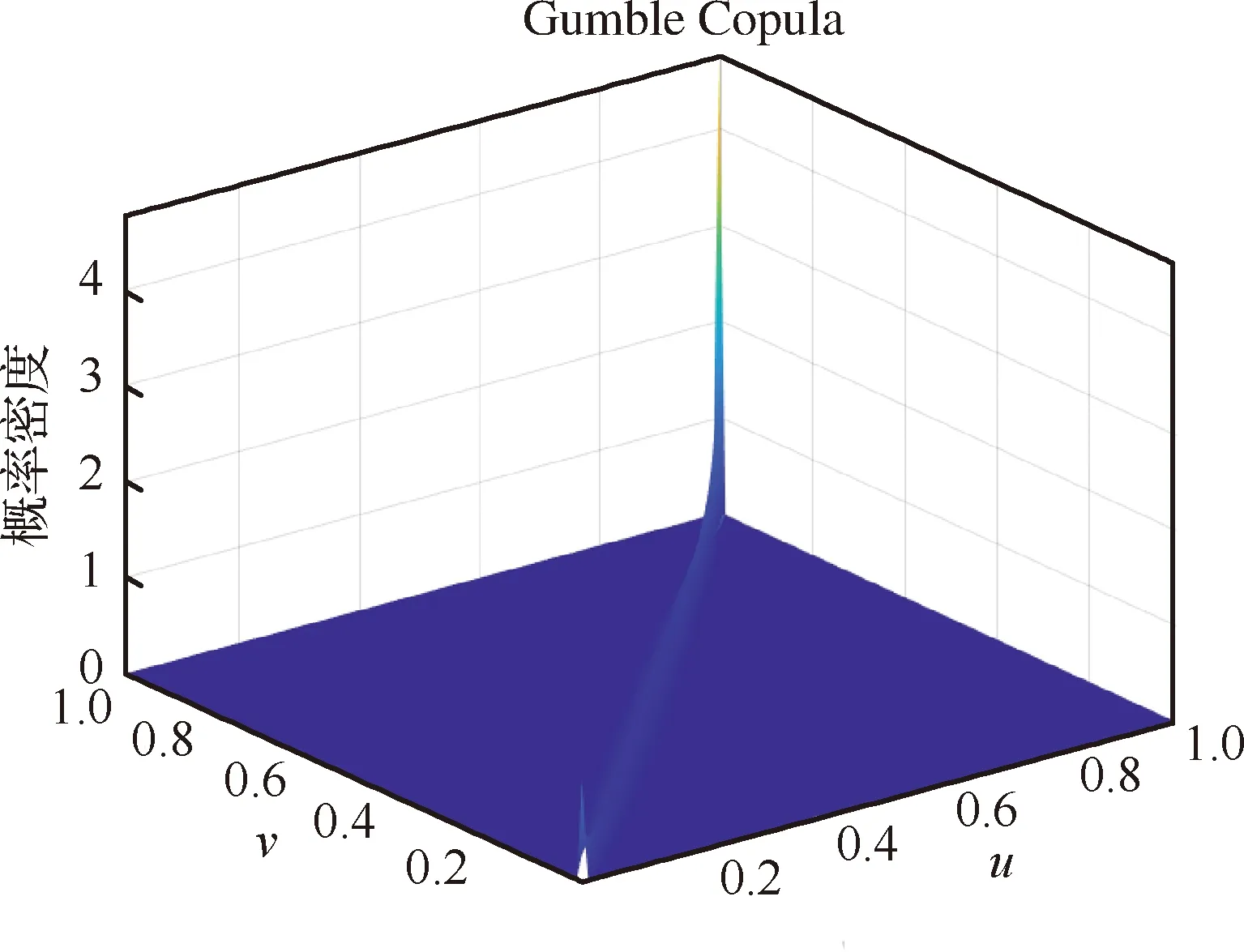
图4 Gumbel Copula模型概率密度Fig.4 Probability density of Gumbel Copula model

将式(38)和式(39)代入到式(40)中，便可得到迎角极值和俯仰角速率极值联合分布概率密度函数(,)。

4 基于吸引域理论和二元极值Copula模型的飞行风险概率计算

综上所述，背景飞机结冰条件下飞行风险量化评估流程如图5所示。

图5 结冰条件下飞行风险量化评估流程Fig.5 Process of flight risk quantitative assessment under icing conditions

4.1 典型飞行想定

结冰相关安全关键飞行参数有迎角与飞行速度等，当驾驶员没有意识到结冰的严重程度时，一旦操纵不当导致这些运动参数超过其安全边界，便有可能发生飞行事故。将所有可能的结冰致灾因素考虑到风险评估中会提高风险预测的准确性，然而这会使工作变得异常繁琐，而且没有必要。考虑到迎角通常是边界保护问题研究中首要考虑的因素，本文在纵向通道上，以典型的驾驶员操纵——升降舵脉冲作为输入，将飞行风险事件的发生定义为飞机状态超出基于迎角和俯仰角速率的二维稳定边界，以此为基准，对结冰后的飞行动力学仿真结果进行分析评估。

之所以选择升降舵脉冲，一方面该操纵被广泛用于结冰后的参数辨识中，能够充分激发飞机的动力学响应,另一方面在驾驶员意识到飞机因结冰高度降低时，由于操纵者对结冰带来的飞行包线萎缩并没有充分的认识，很可能会采用近似于升降舵脉冲的操纵方式来修正高度。

4.2 不同结冰严重程度下的飞行风险概率

以飞行状态超出稳定边界为飞行风险判定条件，采用Gumbel Copula模型计算结冰条件下的飞行风险概率：

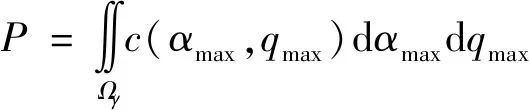
(41)

对于背景飞机，假定飞机以=2 000 m，=120 m/s的初始状态保持水平直线飞行，当结冰严重程度因子=0.1时，吸引域1为

1={,∈|0621 8(-0119 7)-

0274 4(-0119 7)+0608 9≤0046}

(42)

将1及背景飞机常规动力学模型的稳定与不稳定相轨迹投影到-相平面图上，如图6所示。辨识Gumbel Copula模型中的未知参数，结果如表6所示。

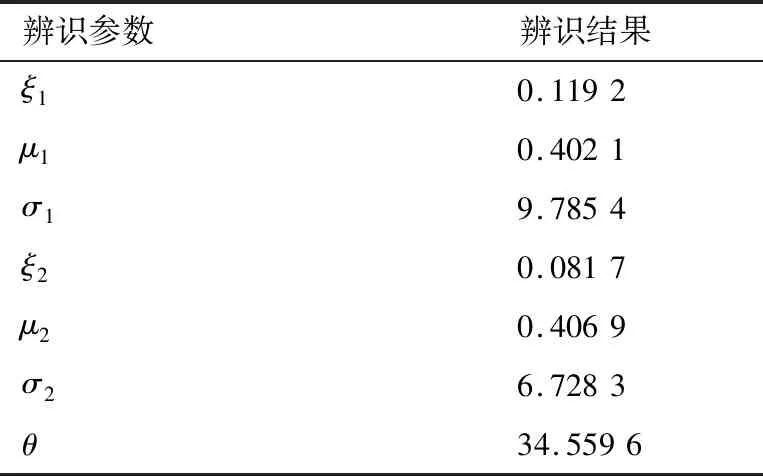
表6 结冰严重程度η=0.1时Gumbel模型参数辨识结果Table 6 Parameter identification results of Gumbel model when icing severity η=0.1

图6 结冰严重程度η=0.1时α-q相平面图与吸引域Fig.6 Phase plane plot of α-q and region of attraction when icing severity η=0.1

将式(42)代入式(41)中，计算出当前结冰严重程度条件下的飞行风险概率为

=887×10

(43)

该飞机处于弱结冰(Trace)状态，按照航空信息手册中的说明，除非飞机暴露于结冰区中较长时间(大于1 h)，驾驶员在穿越结冰区时无需开启防/除冰设备。

当结冰严重程度因子=0.2时，吸引域2为

2={,∈|0601 2(-0127 9)-

0301 7(-0127 9)+0638 3≤0028 2}

(44)

同样，将2及背景飞机常规动力学模型的稳定与不稳定相轨迹投影到-相平面图上，如图7所示。辨识Gumbel Copula模型中的未知参数，结果如表7所示。

图7 结冰严重程度η=0.2时α-q相平面图与吸引域Fig.7 Phase plane plot of α-q and region of attraction when icing severity η=0.2

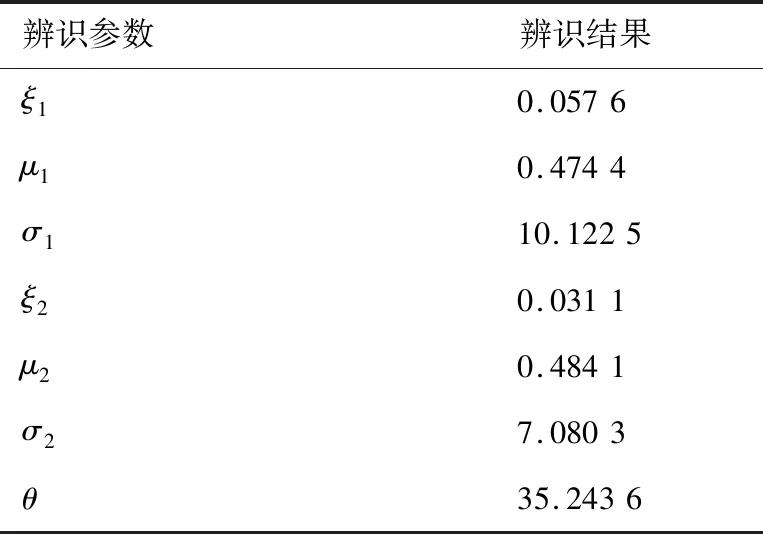
表7 结冰严重程度η=0.2时Gumbel模型参数辨识结果Table 7 Parameter identification results of Gumbel model when icing severity η=0.2

当前结冰严重程度下的飞行风险概率为

=126×10

(45)

该飞机处于轻度结冰(Light)状态，按照航空信息手册中的说明，飞机长时间在目标航迹区遭遇该严重程度的结冰时，驾驶员需要间歇开启防/除冰设备。

当结冰严重程度因子=0.3时，吸引域3为

3={,∈|0542 1(-0147 9)-

0252 7(-0147 9)+0857 8≤0014 4}

(46)

同样，将3及背景飞机常规动力学模型的稳定与不稳定相轨迹投影到-相平面图上，如图8所示。辨识Gumbel Copula模型中的未知参数，结果如表8所示。

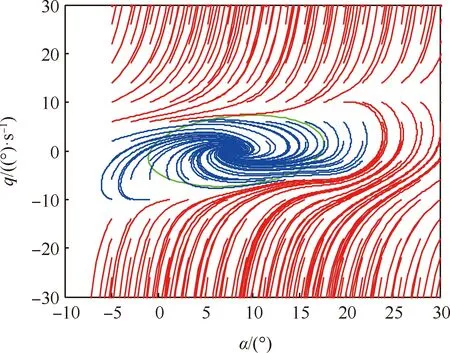
图8 结冰严重程度η=0.3时α-q相平面图与吸引域Fig.8 Phase plane plot of α-q and region of attraction when icing severity η=0.3

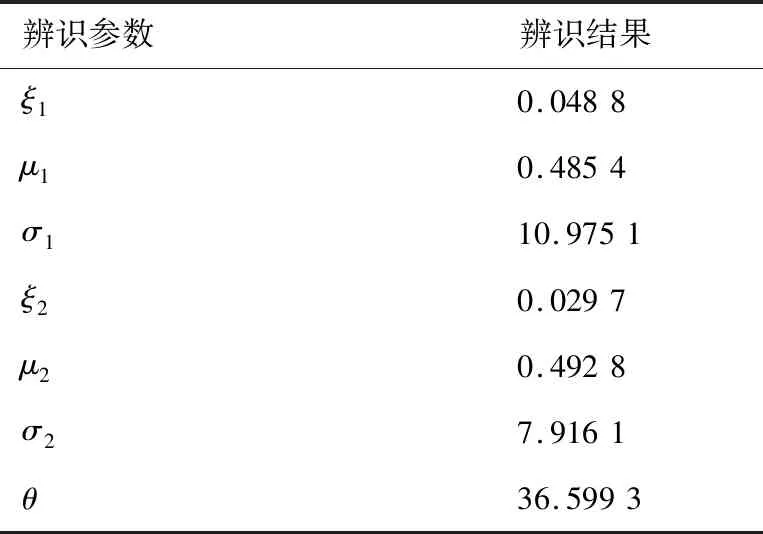
表8 结冰严重程度η=0.3时Gumbel模型参数辨识结果Table 8 Parameter identification results of Gumbel model when icing severity η=0.3

当前结冰严重程度条件下的飞行风险概率为

=742×10

(47)

该飞机处于中度结冰(Moderate)状态，按照航空信息手册中的说明，飞机一旦在目标航迹区遭遇该严重程度的结冰，发生飞行风险的可能性较高，在运行过程中，驾驶员必须一直开启防/除冰设备或者改变路线驶离结冰区域。

由于在进行多项式拟合、风险概率计算的每一步都会引入误差，最终的计算结果很难用一个准确的误差范围去衡量,本文通过对每一步计算结果的检验来进行误差控制。误差的引入主要有以下两个方面：

1) 多项式拟合带来的误差。虽然多项式模型转化过程中引入了误差，但图2所示的相平面对比图说明误差对结果影响不大，究其原因，基于平方和理论的吸引域计算方法是一种偏保守的方法，存在一定的安全裕度，该方法在解决F/A-18飞机控制器对落叶飘模态敏感性分析上得到了应用，验证了该方法的有效性。

2) 应用极值理论带来的误差。虽然极值参数分布的随机性带来的误差不可避免，但只要通过文中所述的检验方法，即可认为误差是可接受的。

5 结 论

本文首先建立了飞机纵向动力学模型和结冰影响模型，基于吸引域理论，得到了不同结冰程度条件下的飞机二维吸引域及稳定边界；建立典型的人-机-环系统模型，运用蒙特卡罗仿真方法，得到了迎角极值和俯仰角速率极值；根据极值理论，建立并确定了适用于结冰条件下飞行风险量化评估的二元极值Copula模型，计算了不同结冰严重程度下的风险概率并对驾驶员操纵提出指导，主要结论如下：

1) 吸引域方法适用于计算飞机飞行的稳定边界，计算结果直观明了。随着结冰严重程度的增加，飞行的稳定边界缩小，导致发生飞行事故的风险增加。

2) 基于吸引域和二元极值理论的结冰飞机飞行风险量化评估方法，能够用来定量地计算不同结冰严重程度下的飞行风险，进而指导驾驶员进行合理的操纵，从而规避飞行危险。

附录A

运用四元数法构建飞机动力学模型：

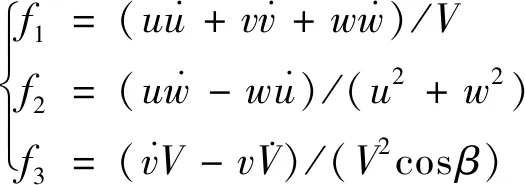
(A1)

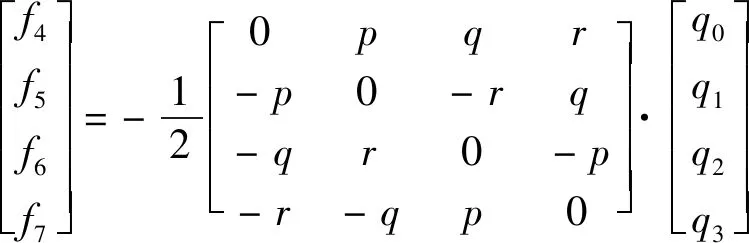
(A2)

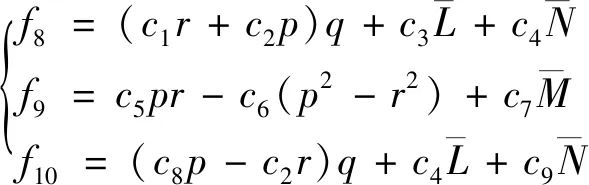
(A3)

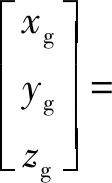
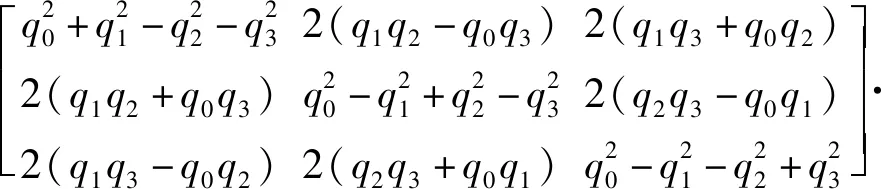
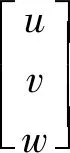
(A4)

同时：

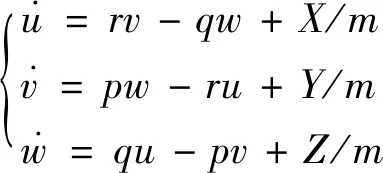
(A5)

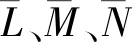
(A6)

(A7)

采用四元数法求解运动方程，能够有效避免出现奇点，同时能够减少三角函数的计算，提高运行效率。四元数满足平方和为1，但其物理意义不够明确，可依据四元数计算出欧拉角，飞机姿态角、、可通过式(A8)～式(A10)计算。在反求欧拉角的过程中，可能出现分母为零的情况，可以通过巧妙编程解决，不影响运动方程求解连续性，同时为减小迭代计算产生的累积误差，每步仿真均将四元数进行归一化处理。

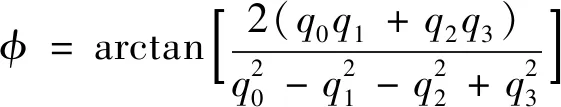
(A8)

=arcsin[2(-)]

(A9)

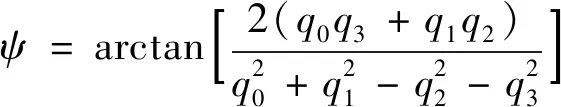
(A10)

附录B

-设序列,,…,为独立同分布的随机变量，当存在常数列{>0}、{}时，满足：

(B1)

则()是非退化分布函数，且()必属于下列3种类型分布之一：

1)Ⅰ型分布

()=exp(-e-) -∞<<+∞

(B2)

2) Ⅱ型分布

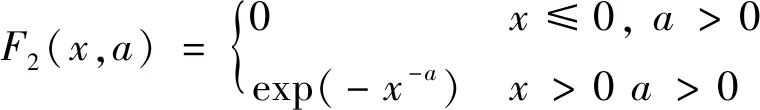
(B3)

3) Ⅲ型分布

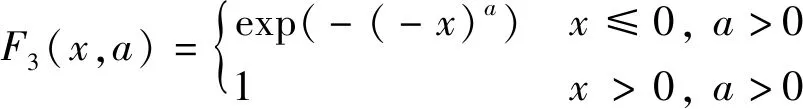
(B4)

上述3种分布分别称为Gumbel分布、Frechet分布、Weibull分布，可统称为极值分布,和称为规范化常数。当=1时，(,1)和(,1)分别称为标准Frechet分布和标准Weibull分布。

进一步引入位置参数和尺度参数，则可以将上述3种类型的极值分布形式统一为

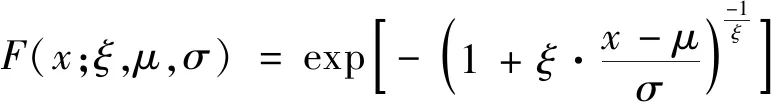
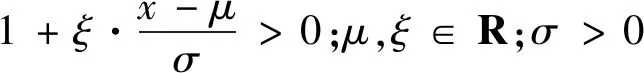
(B5)

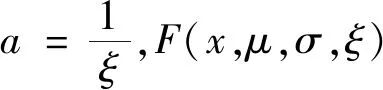
附录C

表C1 迎角极值样本
Table C1 Sample of extreme angle of attack (°)

序号样本值1-58.7788.8948.9888.9979.0186-109.0219.0399.0589.0829.09311-159.1199.1539.1829.2019.22816-209.2519.2729.3059.3179.33221-259.3339.3349.3419.3469.35626-309.3629.3889.4039.4329.45031-359.4749.4989.5279.6019.64336-409.6829.7019.7239.8329.89541-459.96210.00810.05910.16510.19746-5010.23110.38910.41810.48310.532

表C2 俯仰角极值样本
Table C2 Sample of extreme pitch angle (°)

序号样本值1-55.7965.8065.9045.9485.9776-105.9815.9856.0116.0176.02511-156.0466.0756.1056.1516.16316-206.2216.2256.2346.2416.25721-256.2596.2606.2666.2856.29126-306.3176.3306.3726.3746.39831-356.4336.4886.5136.5966.60136-406.6236.6896.7116.7936.84241-456.9086.9717.1327.1747.19846-507.2557.3497.3567.4677.896

附录D

假设联合分布函数具有边缘分布函数()，()，…，()，则∃-Copula函数，满足：

(,,…,)=((),(),…,())

(D1)

若()，()，…，()连续，则唯一确定。