不同承载阶段行星滚柱丝杠副的变形研究*

刘子博，邓 攀，祖 莉，王 凯，黄鸿坤，黄强强

(1.南京理工大学机械工程学院，南京 210094;2.上海船舶设备研究所，上海 200031)

0 引言

行星滚柱丝杠副是一种可实现旋转运动与直线运动之间相互转化的高精密传动机构，具有运动精度高、承载能力强、运行速度高等性能特点，目前可广泛应用于航空航天、军工火炮等极端恶劣的工作环境下，如空间太阳能电池板的展开控制系统，这就要求行星滚柱丝杠副在短时间内承受数倍于额定静载荷的压力下正常运行。因此，对行星滚柱丝杠副承受重载和高过载能力的研究急需深入。

近年来，国内外学者对行星滚柱丝杠副的承载特性开展了深入研究。ZHANG等[1]基于螺距变动量对载荷分布进行理论建模，并通过试验验证了模型的正确性；郑正鼎等[2]比较系统地得出了相关结构参数对行星滚柱丝杠副载荷分布的影响规律；张文杰等[4]基于螺纹牙闭环内变形协调条件，建立了载荷分布矩阵方程，并研究各类误差对载荷分布的影响；ABEVI、JONES等[3,5]分别采用非线性模型法、直接刚度法建立行星滚柱丝杠副轴向刚度模型，并计算其轴向静刚度。综上所述，行星滚柱丝杠副轻载弹性阶段的相关研究已经较为成熟，但仍缺少基于螺纹牙受载不均对轴向刚度分析方面的研究。此外，针对行星滚柱丝杠副塑性阶段的研究较为缺乏，且无行星滚柱丝杠副承载能力的界定分析。

本文基于螺纹牙受载不均现象建立行星滚柱丝杠副轴向刚度模型，引入加工精度系数推导出额定静载荷公式，并采用有限元法对行星滚柱丝杠进行仿真建模，分析在额定静载荷和高过载工况下塑性变形情况；最终通过承载试验，对模型进行验证，进一步获得行星滚柱丝杠副的轴向刚度、塑性变形及承载极限情况。

1 轻载弹性阶段轴向刚度模型建立

行星滚柱丝杠副由丝杠、滚柱、螺母、内齿圈、保持架组成，其中滚柱牙型为圆弧面，丝杠与螺母牙型为三角形。当行星滚柱丝杠副受到轴向载荷时，其产生赫兹接触变形，轴段之间的轴向压缩变形，以及各元件相邻螺纹牙变形。本节综合上述三种弹性形变情况，对行星滚柱丝杠副轴向刚度进行建模，如图1所示，该轴向刚度模型建立于以下假设：

图1 行星滚柱丝杠副轴向刚度模型

滚柱-丝杠侧的载荷分布与滚柱-螺母侧的载荷分布相同；行星滚柱丝杠副每个滚柱受载相同；不存在任何加工误差、装配误差。

由赫兹变形接触公式[6]可知：

(1)

式中，δ为弹性变形量；Q为法向接触力；K(e)为椭圆积分；μ1、μ2为泊松比；E1、E2为弹性模量；∑ρ为曲率和。

由文献[7]可知，当行星滚柱丝杠副受载时，每个螺纹牙受载不均，其载荷分布模型如下：

(2)

式中，P为螺距；N为滚柱个数；Z为单个滚柱螺纹接触数；j为单个滚柱螺纹牙序列号；As为丝杠等效圆柱的横截面积；An为螺母等效圆柱的横截面积。且丝杠和螺母滚道都会与滚柱接触发生弹性形变，其中滚柱i的丝杠-滚柱侧第j对螺纹牙或螺母-滚柱侧第j对螺纹牙产生的轴向接触变形为：

lxij=δxij/sinβ/cosα

(3)

式中，x分别为s、n，代指丝杠-滚柱侧、螺母-滚柱侧；i为滚柱序列；β为接触角；α为螺旋升角。

则滚柱i丝杠-滚柱侧第j对螺纹牙或螺母-滚柱侧第j对螺纹牙的轴向接触刚度为：

(4)

式中，Fxij=Qxijsinβcosα，其为图1中滚柱i第j个螺纹牙受到的轴向力；Kx为丝杠-滚柱侧或螺母-滚柱侧的接触系数。

当行星滚柱丝杠副承受载荷后，受力的每个螺纹牙会发生5种螺纹牙轴向变形[8]：①因弯曲导致的变形δ1；②因剪力导致的变形δ2；③因牙根倾斜导致的变形δ3；④因牙根剪切导致的变形δ4；⑤因径向分力导致的变形δ5。各螺纹牙变形的计算公式如下：

(5)

式中，a为螺纹牙底厚度；b为螺纹中径牙厚；c为螺纹牙顶厚度；δ5y为外螺纹导致的变形；y为s和r；δ5n为内螺纹导致的变形；d0为外螺纹等效直径；D0n为螺母等效圆柱体外径；dpn为螺母等效圆柱体内径；P为螺距；δT为单个螺纹牙总轴向变形。

则丝杠-滚柱侧和滚柱-螺母侧滚柱i的第j对轴向螺纹牙刚度为：

(6)

式中，y为s、n和r，代表丝杠、螺母和滚柱。

行星滚柱丝杠副受载后，相邻承载螺纹牙之间会发生轴向压缩变形，每个压缩单元的长度都为丝杠的螺距，则丝杠、螺母、滚柱的单元轴段刚度为：

(7)

式中，As、An、Ar为等效圆柱横截面积；d0s为丝杠等效圆柱直径；d0r为滚柱等效圆柱直径。

其余丝杠无接触螺纹段可视为圆柱压缩变形，则无接触螺纹段刚度为：

(8)

式中，L为无螺纹接触段理论计算长度。

因此，行星滚柱丝杠副轴向刚度数学模型为：

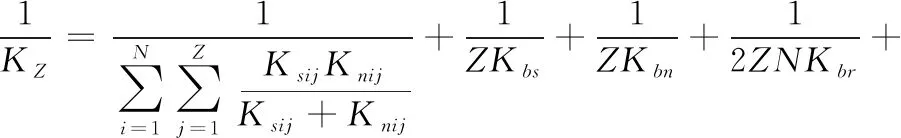
(9)

2 重载及高过载塑性阶段分析

2.1 额定静载荷计算

由于行星滚柱丝杠副与滚珠丝杠副的接触方式、运动特征具有相似性，因此考虑加工精度因素，将精度系数fa引入到轴向刚度公式中，反求出实际承载螺纹牙个数，最终依据ISO-3408-5[9]滚珠丝杠副额定静载荷计算方法求出行星滚柱丝杠副的额定静载荷。

在实际接触过程中，赫兹接触产生的变形占总变形的98%[7]，因此在计算轴向刚度时可忽略螺纹牙变形和轴段变形，最终简化后的轴向刚度Kzj为：

(10)

式中，M为载荷不均匀系数。

参考ISO-3408-4[10]，将精度系数fa引用到式(10)，得到修正后的轴向刚度为：

Kzd=faKzj

(11)

式中，fa取值参照表1。

表1 精度等级表

将Kzd替代简化后的轴向刚度Kzj，可得到单个滚柱等效承载螺纹牙个数Zd：

(12)

通过等效承载螺纹牙个数，求出行星滚柱丝杠副轴向额定静载荷计算公式为：

(13)

2.2 额定静载荷灵敏度分析

为提高行星滚柱丝杠副额定静载荷及静态承载能力,需要进行相关参数的额定静载荷敏感性分析,定量评价结构参数、精度等级等变化对额定静载荷的影响程度。

设额定静载荷的函数表达式[11]为：

Coad=F(X1,X2,X3,X4,X5)=F(fa,Z,N,β,α)

(14)

各参数的初始值依次为0.5、28、11、45、4.67，各参数区间范围为[Xmin,Xmax]，依据控制变量法，控制一个参数在区间范围变化，其余参数均为初始值。

则额定静载荷的数值范围为：

Coad=[Cmin,Cmax]

(15)

式中，Cmin为单一参数变换后额定静载荷最小值；Cmax为单一参数变换后额定静载荷最大值。

行星滚柱丝杠副的额定静载荷的相对灵敏度r为：

(16)

依据式(16)可得到各参数对行星滚柱丝杠副额定静载荷的灵敏度如表2所示。

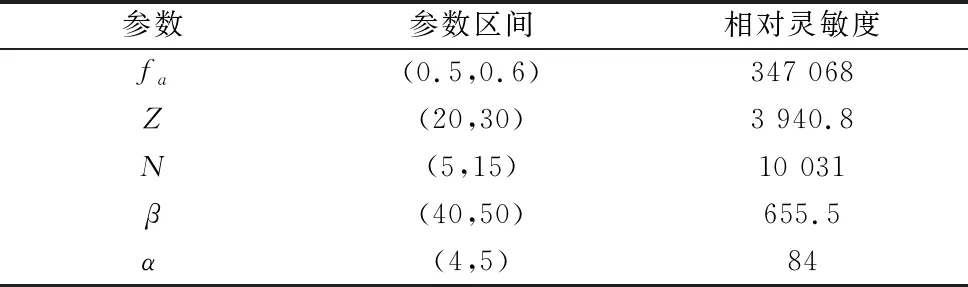
表2 额定静载荷参数灵敏度表

从表2可以得出，精度等级对额定静载荷的影响最大，其次为滚柱数目，影响最小的为导程角，因此对影响程度最大的两个参数进行额定静载荷数值仿真，如图2所示，加工精度等级越高，滚柱数目越多，行星滚柱丝杠副的额定静载荷就越大。

图2 仿真结果图

2.3 有限元塑性仿真

本文选用某公司生产制造的规格为20×5×5的行星滚柱丝杠副，具体参数如表3所示。

表3 行星滚柱丝杠副参数表

由式(13)可求出该型号行星滚柱丝杠副的额定静载荷C0a为100 kN。

通过Workbench软件对行星滚柱丝杠进行塑性仿真分析，研究其轴向力为100%C0a和285%C0a时，行星滚柱丝杠的塑性变形情况。其仿真步骤如下：

(1)将简化模型导入Workbench中，并进行处理；

(2)材料赋予：添加密度、弹性模量和塑性模块；

(3)接触设置：接触对的接触方式均为Frictionless，初始接触均为Adjust to touch，接触行为为Asymmetric，并且每步迭代都更新接触刚度值；

(4)网格划分：对模型进行Body sizing六面体网格划分，再对接触面进行细化网格；

(5)边界条件创建：如图3所示，在丝杠-滚柱模型中，对丝杠添加displacement约束，对滚柱施加固定副；在滚柱-螺母模型中，对滚柱添加displacement约束，对螺母施加固定副；

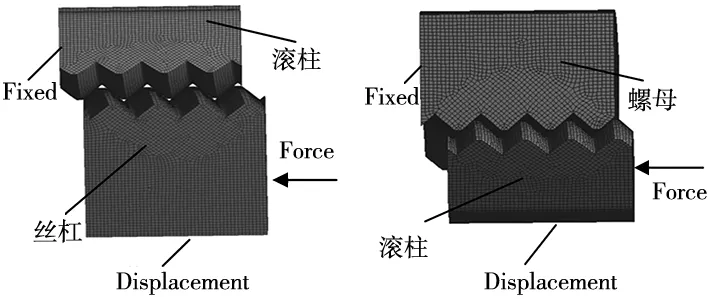
(a) 丝杠-滚柱侧 (b) 滚柱-螺母侧

(6)载荷步施加：设置多个载荷步，通过载荷子步控制每个载荷步，实现加载-卸载过程；

(7)结果查看：添加接触对的位移图，观察每个螺纹牙产生塑性变形的情况。

2.4 仿真结果分析

图4为当轴向载荷为100%C0a时，丝杠-滚柱侧和滚柱-螺母侧的塑性变形情况。图4a～图4b中丝杠-滚柱侧丝杠和滚柱螺纹牙产生的最大塑性变形量分别为4.137 μm、3.745 8 μm；图4c～图4d中滚柱-螺母侧滚柱和螺母螺纹牙产生的最大塑性变形量分别为2.115 μm、1.954 5 μm。因此在100%C0a轴向载荷下，行星滚柱丝杠副产生11.952 3 μm的塑性变形。

(a) 丝杠-滚柱侧丝杠变形图 (b)丝杠-滚柱侧滚柱变形图

图5为轴向载荷为285%C0a时，螺纹牙的变形情况，可以清晰地看出，每个螺纹牙靠近牙顶部分出现严重压痕，且最左侧螺纹牙塑性变形最大。

图5 轴向载荷为285%C0a的丝杠变形图

3 承载测试

为了研究行星滚柱丝杠副承载的3个阶段，即轻载弹性阶段、重载塑性阶段以及高过载塑性阶段。本文利用了一种垂直加载试验台，如图6所示。

1.状态监控模块 2.加载横梁 3.600 kN压力传感器 4.丝杠防转装置 5.压盘 6.被测丝杠副 7.接触式位移传感器 8.丝杠夹具盘 9.螺母基准盘 10.工作台

通过上述行星滚柱丝杠副垂直加载试验台，得到轻载弹性阶段的试验刚度、重载塑性阶段及高过载塑性阶段的轴向载荷-轴向变形量曲线和塑性变形量，其具体试验步骤如下：

(1)载荷初始值为8 kN、试验加载的最大载荷为Fa、最大加载步进值为5%C0a，则Fa的计算公式如下：

Fa=F0+(i-1)5%C0a

(17)

式中，F0为初始最大载荷20 kN；i为测试次数。

(2)通过驱动伺服电机，使加载横梁以0.2 mm/min速度向下移动，产生轴向力并通过数据采集卡实时采集压力传感器的轴向力数值。

(3)加载到最大载荷Fa时，进行卸载，驱动加载横梁向上移动，当载荷卸载到8 kN时，伺服电机停止驱动，并记录完全卸载后位移传感器的值li。

(4)对采集到的数据点进行轴向载荷-轴向变形量曲线拟合，得出加载、卸载刚度值，则第i次试验发生的累积塑性变形量Si的计算公式如下：

(18)

(5)将位移传感器初始化处理，使位移传感器初始值为0，令i=i+1，返回(2)。

(6)若试验过程中出现曲线在某点处发生急剧变化，或试验刚度发生大的波动，则停止试验，检查丝杠是否良好，如发生严重卡滞、丝杠形貌有严重压痕，则结束试验；若无上述情况发生，则继续试验。

4 结果与分析

依据上节的试验流程对该行星滚柱丝杠副进行承载测试试验，获得在不同轴向载荷下加载过程和卸载过程的轴向载荷-轴向变形量曲线，如图7、图9和图10所示。图7是最大轴向载荷为 45 kN(45%C0a)时的曲线图，从中可以看出，在最大轴向载荷处于未超过45 kN情况下，当轴向载荷完全卸载完成后，其轴向载荷-轴向变形量曲线可以回到原点，由此可以判断，在轴向载荷未超过45 kN时，该型号行星滚柱丝杠副仅处于轻载弹性阶段。因此，将20 kN～45 kN的刚性实验值与理论值进行对比，由图8所示，通过理论刚度与试验刚度之间的相对误差在6%以内，进而验证行星滚柱丝杠副轴向刚度模型的正确性。

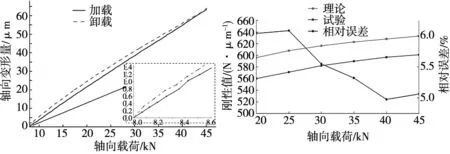
图7 载荷-变形量曲线(Fa=45%C0a) 图8 轻载弹性阶段刚性对比曲线(20 kN～45 kN)

从图9a可以看出，在最大轴向载荷达到50 kN(50%C0a)后，当轴向载荷完全卸载后，其轴向载荷-轴向变形量曲线并没有回到原点，这表明轴向载荷达到50%C0a时，该样件已经发生了屈服，进入了塑性变形阶段，产生的塑性变形量为0.65 μm。当继续增加轴向载荷时，单次试验的塑性变形量也在逐渐增大，从图9b可以看出，当最大轴向载荷达到额定静载荷(100%C0a)时，其产生的塑性变形量达到了1.42 μm，累积塑性变形量达到了12.77 μm，与仿真结果11.952 3 μm之间的相对误差为6.84%，存在相对误差的原因：由于加工误差的存在，导致有些螺纹牙并未受载，而仿真是按照每个螺纹牙均接触受力进行分析。

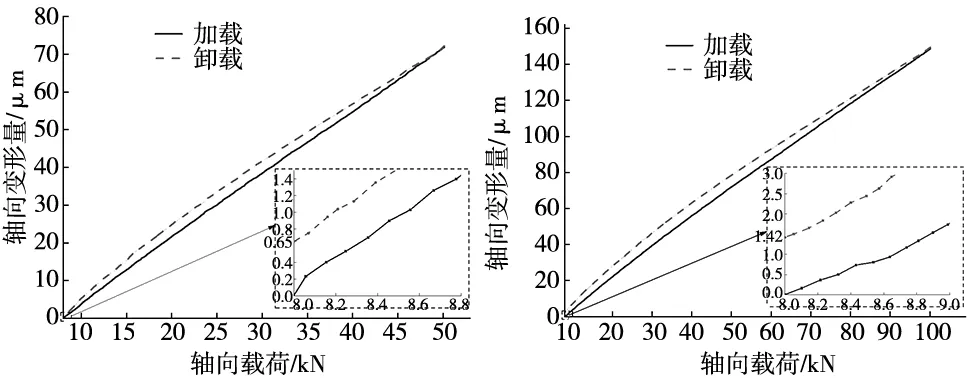
(a) 载荷-变形量曲线(Fa=50%C0a) (b) 载荷-变形量曲线(Fa=100%C0a)

图10a、图10b分别是最大轴向载荷为245 kN(245%C0a)、285 kN(285%C0a)时的曲线图，从中可以看出，当轴向载荷达到233 kN(233%C0a)时，其加载过程的载荷-变形量曲线不再按照之前的趋势变化，而是出现了一个受力变形曲线转折点，转折点之后的曲线斜率在不断变大，即单位轴向载荷对应下的单位轴向变形量在不断变大，但其卸载状态依旧为弹性卸载状态。当轴向载荷达到285%C0a时，加载的轴向载荷-轴向变形量曲线的斜率接近无限大，即应力不再增加，应变持续增加。

(a) 载荷-变形量曲线(Fa=245%C0a) (b) 载荷-变形量曲线(Fa=285%C0a)

图11a为最大轴向载荷增至100 kN(100%C0a)，卸载后的丝杠滚道形貌，可以观察到其丝杠滚道形貌无明显压痕，用手盘动螺母，其传动情况良好，有轻微卡滞现象；当轴向载荷增至285 kN(285%C0a)，卸载后的行星滚柱丝杠副出现严重的卡滞现象，其传动功能基本完全丧失，且观察图11b丝杠滚道形貌，可以看到螺纹牙靠近牙顶部分出现严重压痕，且从最右侧滚道至最左侧滚道，压痕在不断变大，与仿真得到的相邻螺纹牙塑性变形趋势一致。因此可说明在承载过程中，滚柱的螺纹牙承受的载荷不均，且丝杠与滚柱接触位置靠近牙顶侧。此时，行星滚柱丝杠副出现严重的卡滞现象，其传动功能完全丧失。由此可认为型号为20×5×5的行星滚柱丝杠副可承受的极限载荷为285 kN(285%C0a)。

(a) 100 kN卸载后的丝杠滚道形貌 (b) 285 kN卸载后的丝杠滚道形貌

5 结论

本文在不同承载工况下对行星滚柱丝杠副进行变形及承载极限研究，在轻载弹性阶段，基于载荷分布理论建立行星滚柱丝杠副轴向刚度模型；在重载和高过载塑性阶段，基于等效承载螺纹牙数推导出额定静载荷公式，研究其相关设计参数对额定静载荷的影响程度。随后，基于有限元法对行星滚柱丝杠副进行仿真建模，研究了其受重载和高过载时塑性变形情况；最终，通过承载试验对轴向刚度理论和有限元模型进行验证，其理论、仿真及试验结果表明：

(1)由丝杠滚道形貌及仿真结果看出，其相邻螺纹牙的塑性变形情况并不相同，验证了螺纹牙受载不均，且在轻载弹性阶段内，理论刚度与试验刚度之间的相对误差小于6%，因此验证了理论刚度模型的正确性。

(2)加工精度等级对额定静载荷影响最大，其次依次为滚柱数目、螺纹牙数、接触角、导程角。

(3)在额定静载荷100%C0a下，理论仿真得到的塑性变形量与试验测到的塑性变形量之间的相对误差值为6.84%，验证理论塑性仿真模型的正确性。

(4)在高过载塑性阶段，当轴向载荷-轴向变形量曲线出现转折点后，且其斜率趋于无穷大时，即最大轴向载荷为285 kN(285%C0a)时，行星滚柱丝杠副的传动性能已完全丧失，其滚道形貌出现严重压痕且与仿真结果吻合，此时可认为行星滚柱丝杠副其可承受的极限载荷为285 kN。