基于模糊规则的数据异常检测系统
2022-06-29周爱平陈为高杨彦飞杜垣江贾子熙
周爱平,常 俊,陈为高,杨彦飞,杜垣江,贾子熙
(1.国家能源集团煤炭运输部,北京 100011;2.胜利能源公司工程部,沈阳 110000;3.中国神华煤炭管理部综合处,北京 100011;4.中煤科工集团沈阳设计研究院有限公司,沈阳 110000;5.东北大学机器人科学与工程学院,沈阳 110819)
0 引言
异常检测(anomaly detection)是指利用数学概率计算或深度学习等机器学习的方法识别数据中的“异常点”。常用的异常检测算法有:基于统计模型、基于距离、基于密度、基于聚类[1]的方法。但是这些方法通常只适用于低维空间的异常检测,对于高维空间的异常检测,通常表现较差。
在异常检测方面,丁小欧等[2]针对多维时间序列数据,提出了一种基于序列相关性分析的多维时间序列异常检测方法;王伟等[3]针对工业数据的异常检测,提出了一种基于PU学习的工业控制系统异常检测方法;李超等[4]对工业控制系统中的基于单类支持向量机异常检测方法作了深入的研究。张仁斌等[5]对传统k均值算法作了改进,将改进后的K-均值算法与传统自回归模型结合,对异常数据进行检测。
针对传统机械生产领域中各种基础设备的异常数据检测及异常预警,本文提出了一种基于模糊规则的数据异常检测系统框架,分为检测和预测两部分。对于异常检测,预期效果是准确率达到80%以上;对于异常预测,主要是在理论上进行探索,尝试根据历史数据,以下一时刻的样本标签为预期输出,对数据进行训练,尝试发现数据中存在的异常趋势特征。整个系统框架具有良好的可扩展性和交互性,可方便实现不同模型之间的切换和结果的可视化。
1 异常快速检测模块
1.1 数据异常处理模型
在异常处理模型中,本文嵌入整合了支持向量机、决策树、随机森林、Logistic回归等基本模型。其中,支持向量机模型准确率高、训练速度较慢,适用于中小型数据量的场景;决策树模型训练速度快、泛化性能较差,适用于单一场景的异常处理;随机森林模型训练快、泛化性强,易受到强噪声样本影响;逻辑回归模型训练快,无法解决非线性问题,准确率相对较低。当数据量较大且数据噪声样本较少时,建议选择随机森林模型。
对于异常检测,SVM的输出为标准的无阈值输出:
f(x)=h(x)+b
(1)
式中,f(x)为模型输出;b为偏置;h(x)的计算公式如下:
(2)
式中,yi为模型输出的第i个分量;ai为模型的第i个权重系数;k(xi,x)为核函数;xi为样本第i个分量;x为原始样本。
利用sigmoid-fitting方法[6]将标准SVM的输出结果进行处理,转换成后验概率为:
(3)
式中,A、B为待拟合的参数;f为样本x的无阈值输出。sigmoid-fitting方法的优点在于保持SVM稀疏性的同时,可以良好的估计后验概率[7]。在进行异常检测及预警时,可以据此计算异常程度值。
在应用决策树模型时,样本的类别概率是叶子中相同类别的样本的分数,据此可以对样本的异常程度值进行计算。例如,测试样本数据对应的叶子节点中有7个正常样本及3个异常样本,那么这个样本的异常程度值为0.3。
随机森林是一个包含多个决策树的分类器。在应用随机森林进行异常检测时,样本的异常程度值为森林中树木输出的异常程度值的平均值。
Logistic回归是一种广义线性回归,常用于分类问题。其计算公式如下(Sigmoid函数):
(4)
式中,w为权重;x为样本;b为偏置;y为模型输出,其取值范围为[0,1]。在异常检测时,y表示异常程度值,0表示“正常”,1表示“异常”。
1.2 模糊规则
模糊规则,本质是定义X与Y的二元模糊关系R。模糊规则的一般形式为:“IfxisAthenyisB”。 “xisA”称为前提,“yisB”称为结论。
传统的分类模型如随机森林等,往往直接输出样本的类别(即样本是否异常)。在应用模糊规则时,首先根据基本模型,计算出样本数据的异常程度值p。然后将异常程度划分为四个级别:非常小、较小、较大、非常大。同时,将异常等级分为0级和1级(0级表示正常,1级表示异常),并且定义如下规则:
①异常程度值非常小,异常等级为0级;
②异常程度值较小,异常等级为0级;
③异常程度值较大,异常等级为1级;
④异常程度值非常大,异常等级为1级。
对于不同的异常程度级别,定义隶属度如表1所示。

表1 模糊规则隶属度表
对于p=0.2,其满足p<0.3,由规则①~规则④,计算出异常概率L1如下:
L1=0.7×0+0.2×0+0.1×1+0×1=0.1
则相应的正常概率L2为:
L2=1-L1=0.9
由于正常概率较大,因而将此数据记为正常。同理可以对其他数据进行判断。
1.3 数据异常检测及异常预警
在实际工业生产过程中,真正具有实用价值和研究意义的是对于异常发生的预警,通过合理的预警可以更早更及时的做出调整,以减少因为异常而带来整条生产线停工的损失。
对于大规模数据的异常检测,在经过预处理后,将数据输入到异常检测模型中,可实现异常数据的快速检测;对于异常预警,本文创新性的提出了使用已有的数据和数据标签,将异常发生之前的数据进行标注。具体来说,首先统计真实异常发生前一段时间内的数据特征最大值,作为新的特征,然后将真实异常数据的标签作为预期输出,进行模型训练工作。对于异常预警,首先对数据做如上标注,然后利用决策树算法计算异常程度值,之后结合模糊规则,以实现对下一时刻异常发生的预测,即实现预警功能。
2 异常概率计算模块
对于数据拟合预测,主要思路是利用数据在时间序列上的规律,实现对数据特征取值的预测,尤其是对缺失特征值的预测。数据拟合预测分为两种:一种是根据时间序列的规律,进行下一时刻数据的拟合预测;另一种是根据多维数据之间的内在联系,对缺失的特征数据进行预测。在数据拟合预测模块,本文嵌入了循环神经网络(RNN)、长短期记忆网络(LSTM)、多层感知机(MLP)等模型,对时间序列数据进行拟合预测。
RNN是一类用于处理序列数据的神经网络,易出现梯度消失问题;LSTM是对普通RNN模型的改进,解决了梯度消失问题,即对于较长的时间长度序列,LSTM拟合效果较好;MLP是一种前馈人工神经网络模型,训练速度快,但是当数据量特别大时,易出现过拟合问题。当数据量较大且时间跨度较长时,建议选择LSTM模型。
3 实验方法和过程
为了验证本文方法的通用性,在多个数据集上进行了实验,这些数据源自于不同背景,在数据量及数据特征维度上差异较大,能够对本文方法进行更为合理的检验与评价。
3.1 实验数据集
为了尽可能符合实际工业生产领域数据的特征,共选择了5组真实数据。前三组数据含有标签,用于异常检测及预警;第四组数据不含标签,用于拟合预测;最后一组数据为真实的电机运行数据,记录了异常发生前电流、电压等指标的变化情况,用于进行模型验证,验证模型的异常预警效果。各数据背景来源如下:
(1)第一组数据(data_01)来源于一个存储系统,共20列。其中Timestamp为时间戳,Labels表示是否异常,其他列表示4条短传送带及2条导轨对应的3个传感器的数据,数据记录了包裹运行时传感器到机器边缘的距离;
(2)第二组数据(data_02)是从一个零件生产线获取的多个零件温度数据。在这些零件的生产过程中,零件温度对合格程度有着较大影响。数据共38列,其中Timestamp列为时间戳,Labels表示零件是否异常(Labels=1表示异常),其余列表示各零件温度;
(3)第三组数据(data_03)记录了煤矿生产时的机器设备温度。当机器设备发生故障时,设备温度往往高于正常值。数据共3列,Timestamp列为时间戳;var_1表示机器设备温度,取值范围为[20,120];Labels表示设备是否异常(Labels=1表示异常);
(4)第四组数据(data_04)为单维度数据,记录了工业生产中相对湿度的变化情况。数据共2列,Timestamp列为时间戳,var_1表示相对湿度;
(5)第五组数据(data_05)为电机运行状态真实数据,其中记录了电机转速、电压数据、电流数据在真实异常前的变化趋势。
各个数据集的主要信息汇总如表2所示。
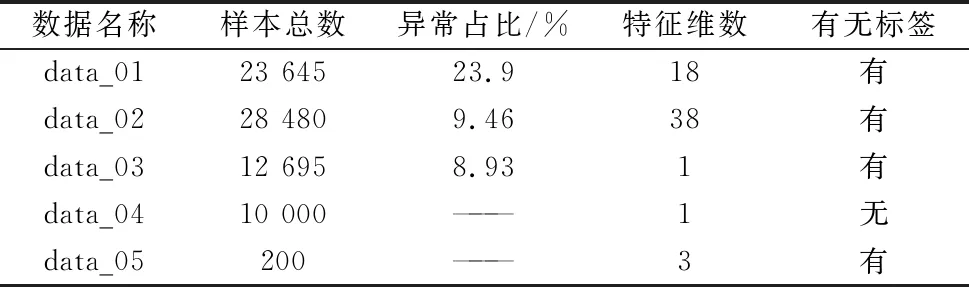
表2 数据集基本信息
3.2 参数设置
在异常处理模块,对于每组数据,我们每次都会随机选择其中的75%作为训练集,然后我们将余下的其他数据作为测试集,这样可以更为客观的验证模型的效果。接下来我们将训练次数根据模型不同分别设置为{10,100,10,100},损失函数为二分类交叉损熵,评价指标为准确率。此外,考虑到实际需求,加入了召回率这一指标。评价指标计算公式如下:
(5)
(6)
式中,TP为True Positive;FP为False Positive ;FN为False Negative。在计算过程中,为了更加有效的反映出异常的检测准确率和召回率,所有的计算均是按单纯异常的数据进行计算。
在数据拟合预测模块,我们将滑动窗口长度设置为5,即将(t-5,t-4,...,t-1)的特征数据作为输入,将t时刻的数据作为期望输出;训练集比例设为75%,迭代次数设为10。同时选取R2评分函数作为模型的评价指标。R2评分函数计算如下:
(7)
4 实验结果及分析
4.1 数据异常检测结果及分析
表3为data_01、data_02和data_03数据集在不同检测模型下的准确率和召回率结果。
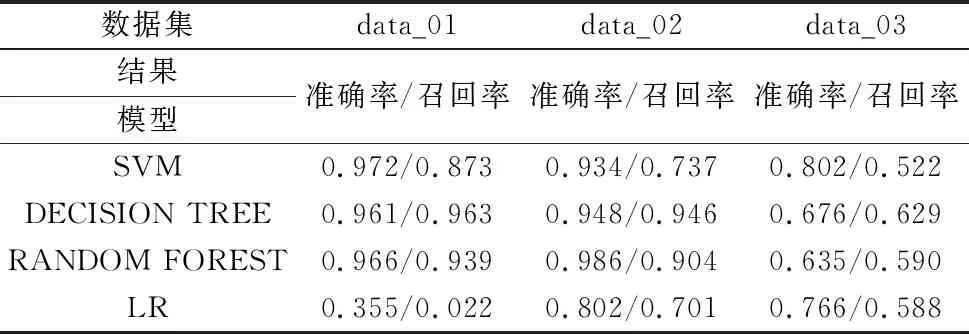
表3 异常检测准确率召回率
可以看出,对于采用任意一种模型进行单纯的异常检测而言,数据的维度对于检测的准确率起到了非常重要的影响。可以看出,决策树和随机森林算法对于多维度的数据的检测更加高效准确,而逻辑回归算法则更适用于单维度的数据检测,支持向量机算法则由于其核函数的存在,在低维数据和高维数据中都能够获得相对均衡额效果,这是由其本身的模型结构所决定的。多数据维度能够更加真实的反映实际工业生产过程中多变量因素的情况。
对于传统的不加模糊规则的方法在理论上更加适用于单维度或者少维度数据的异常检测,但是实际工业生产中一件设备的异常发生往往是由多个因素共同作用的结果,而从多参数的高维数据空间进行数据的检测往往不能取得很好的结果,为此提出了加入了模糊规则,将得到的异常程度值进行状态模糊化,可以更好的对应标签的属性,能够得到更好的准确率和召回率。
4.2 数据异常预警结果及分析
理论上在异常发生之前数据会呈现出一定的变化趋势,通过捕获这种变化趋势可以在一定程度上实现异常发生的预测。按照这种思路,可以将实际的正常异常标签进行预测报警状态的扩充成为三种或者更多种状态,但是实际数据中的异常往往是异常集中在一起较难处理,所以常常无法取得较为理想的效果。
为此采用基于决策树的算法,将原始数据进行预处理之后,在固定的时间步长中取出每一维度数据中最大值作为新的特征值,取时间步长之外下一时刻的状态作为标签,然后进行回归计算和模糊规则映射,通过深入挖掘在异常发生之前的趋势,可以在动态数据产生的过程中,通过捕获当前数据并结合前几个时刻的数据,得到下一时刻可能的状态值,从而实现下一时刻异常的预测预警。表4为三个带标签的数据集按照异常预测模式[8]进行测试后的异常预警准确率和异常预警召回率。分析下述实验结果可知,在进行数据异常预警时,维度特征高的数据表现更佳。

表4 异常发生预警准确率
同时对比了在固定时间步长中对同一维度的数据使用max(最大值)和mean(平均值)两种不同的操作,其结果如表5所示。

表5 不同处理方式下的准确率/召回率
采用最大化的处理方式在特征维度较低时可以获得略好的结果,而当特征维度较高时,两种方法的性能相当。这主要是两种方式对于不同的因素会学习到不同的权重,在维度较高时其权重相对分散,造成其结果并没有太大的差距。
4.3 数据拟合结果及分析
本文介绍了两种不同数据拟合的方式:未缺失数据的拟合预测和缺失数据的拟合预测;前者是根据原始数据对目标数据进行拟合预测,后者是指多维度数据中的某一维度数据是缺失的,这对于数据的拟合预测而言有一定的难度。对于缺失数据的拟合预测,通过分析其他维度的数据与该维度的数据关系,然后进行拟合预测,这对于实际工业现场因故障造成数据丢失的数据获取具有重要意义。
对于数据拟合预测效果的评估,使用R2得分来衡量拟合的效果。表6和表7是对不同数据集按照两种拟合方式进行预测的效果和R2得分的表现。

表6 缺失数据拟合R2得分

表7 未缺失数据拟合R2得分
通过上述结果可以明显看出未缺失数据拟合的效果要远好于缺失数据的拟合效果。图1为缺失数据拟合预测时在LSTM网络按照时间步长为5,迭代次数为10的效果图。图2为未缺失数据在LSTM网络按照时间步长为5,迭代次数为10的拟合预测效果图。

图1 缺失数据拟合效果示意图 图2 未缺失数据拟合效果示意图
同时,为了更加有效地说明问题,将data_04设置为标准的正弦波变化规律的数据,然后进行拟合,如图3所示。

图3 规律数据拟合效果示意图
可以看出,在数据预测方面,RNN、LSTM、MLP在两个数据集上的表现相近,LSTM模型预测的效果最佳。同时经过实验发现,对于数据的拟合在很大程度取决于预测的形式,对于未缺失数据的预测,相较于原来的数据变化趋势会存在一种滞后的现象;而对于缺失数据的预测效果,则在很大程度上取决于数据形式,对于变化极不规律的数据无法做到精准的拟合预测,这两个结果也从侧面表明了对于时序数据的拟合无法做到完全的预测,只能近似得到其变化趋势和数值。
4.4 异常预警模型验证
为了验证本文模型的异常预警效果,针对第5组数据进行了模型验证,数据整体情况如图4所示。

图4 电机运行状态变化趋势图
其中曲线1表示电压变化趋势,曲线2和3分别表示电流、电机转速变化趋势。曲线的终点处为故障点,即此时的机器发生故障。由于数据量相对较少,选取全部数据对模型进行训练,效果如图5所示。

图5 异常程度变化趋势图
图5中曲线为模型预测的异常程度变化趋势。对应图4可以看出,当电流急剧增加时,异常程度也显著增加;从时间上看,异常程度的趋势稍稍滞后于电流变化趋势。这也在一定程度上说明,对数据中的异常点进行准确预测,在理论上存在很大难度。通过对机器运行数据的分析,在真实异常发生前进行预警,是一种值得尝试的研究思路。
5 结论
本文提出了一个基于模糊规则的异常数据检测系统框架,该框架不但能实现对异常数据的高效检测,同时在数据异常预警方面具有良好的表现。在兼具良好数据检测模型和算法,创新性的提出了使用决策树算法结合模糊规则实现了对下一时刻异常状态的预测算法,对异常预测进行了一定的探讨与尝试。
