基于改进D*算法的巡检机器人路径规划

2022-06-29黄晓华马东明翁亚华

组合机床与自动化加工技术 2022年6期

秦旭，黄晓华，马东明，翁亚华

(南京理工大学机械工程学院，南京 210014)

0 引言

巡检机器人需要在工作场景中规划出一条从初始位置到目标位置的路径[1-2]，该路径应满足路程短、效率高、安全性好等一系列要求，并且必须能够避开沿途的静态和随机动态障碍物[3]，路径规划的好坏直接决定了巡检任务是否能够顺利完成。因此，路径规划对于巡检机器人的任务完成起到举足轻重的作用。

目前较为常用的路径规划算法有Dijkstra算法、A*算法。Dijkstra算法可以在实际环境中搜索一个节点到其他任意节点的最短路径[4]，属于贪心算法的一种；A*算法是在Dijkstra算法基础上进行改进，融合了贪心思想和启发思想，使用启发信息来引导搜索方向，故又称启发式算法[5]，并可以添加安全约束[6]。然而，Dijkstra算法与A*算法在遇到动态障碍物时，只能进行重复规划，效率较低；而在巡检机器人实际工作过程中，可能会出现动态障碍，于是就产生了D*算法[7]，D*算法又称动态A*(dynamic A*)算法，与A*算法类似，不同在于是从终点到起点进行反向搜索。

但是D*算法也存在着一些问题，D*算法以长度优先，并且向周围8个子节点进行扩展搜索，生成的路径会产生一些不必要的转弯，会增加巡检机器人的功耗和时间；长度优先的准则也导致生成的路径某些时候会从两个障碍物之间穿过，并未考虑到机器人本身的外形尺寸[8]。对此，许多学者对D*算法也做出了一些改进，张贺等[9]基于动态窗口法，将 A*算法与D*算法结合，最大程度确保了路径精度。刘晓涛等[10]提出了一种基于支持向量机的D*改进算法，规划出较为平滑的动态路径。史久根等[11]针对D*算法搜索空间较大的问题,引入了抽象分层思想,将环境结构化为层次图，分段搜索，提高了搜索效率。

上述文献中的方法均在一定程度上改进了D*算法，但依然存在一些弊端：①所得路径与障碍物之间具有相对较近的距离，现实生活中，机器人应时刻与障碍物留有相对适中的距离；②为了保证路径规划时的效率从而增加了路径的拐点数，未做到两者间的平衡。

因此，本文提出一定的优化方案，优化代价估计函数并引入平滑度函数，在降低所得路径拐点数目的同时又提高了算法效率；控制了路径与障碍物之间的距离，考虑到了实际应用过程中追求的低功耗和安全性，这些在制造行业的运维过程中都是十分必要的。

1 问题描述

1.1 地图建模

在进行路径规划前，首先要对巡检机器人所处的真实环境进行地图建模，常用的地图主要有栅格地图、拓扑地图、语义地图等。其中栅格地图数据结构简单、能有效表达空间的可变性[12]。故本文采用栅格法对巡检机器人的工作环境进行二维模型搭建。

为了验证最终算法的通用性，用randi函数随机生成静态和动态障碍物(生成的栅格地图见后续仿真图)。

不同类型的栅格区域的含义如表1所示。

表1 栅格类型含义

1.2 D*算法

1.2.1 D*算法简介

D*算法又称动态A*算法，是一种动态逆向扇形搜索算法，逆向的搜索机制保留了地图成本，避免了回溯的高计算成本，这也是D*算法最大的优点。相比于A*算法，D*算法在某些动态环境下搜索效率更高，与另一些启发式算法相比，D*算法计算量小，实现起来比较简单，所以D*算法在路径规划和人工智能等方面得到了广泛的应用。

首先，D*算法的核心思想之一就是路径优劣评价公式，表达式如下：

f(n)=g(n)+h(n)

(1)

式中，n为当前状态；f(n)为从初始状态经由状态n到目标状态的代价估计；g(n)为初始状态到状态n的实际代价；h(n)为状态n到目标状态的代价估计，又称启发函数。

对于两个状态之间的代价，在实际应用过程中，通常以距离作为代价值；对于二维空间内的两个点(x1,y1)、(x2,y2)，又有几种不同的计算机制作为距离的度量，主要有欧氏距离、曼哈顿距离，这些度量机制相应的表达式分别如下：

(2)

dManhattan=|x2-x1|+|y2-y1|

(3)

在D*算法中，常用的是欧式距离作为代价值。

其次，与A*算法类似，D*算法同样定义了两个列表合集：openList与closeList；openList表由待考察的节点组成，closeList表由已经考察过的节点组成，类似于Dijkstra算法中的U集合和S集合，当closeList表中出现目标节点时，程序停止。

对于上文提到的启发函数h，在D*算法中，若Y为X的父节点，设两个节点X，Y之间的代价为C(X,Y)，则有h(X)=h(Y)+C(X,Y)；当X状态发生变化后(如前进过程中原有自由空间遭遇动态障碍物)，那么h(X)会发生改变，设k(X)取变化前后最小的值。

最后，在D*算法的流程中，还定义了两个非常重要的状态：Lower态和Raise态；Lower态代表在机器人行进过程中并未发生突发情况，地图信息如同初始规划一样，即h(X)=k(X)；若在原始规划的路径上的一个或多个节点变为了动态障碍物，如图2所示，则可知此时C(X,Y)=∞，此时h(X)>k(X)，称为Raise态。此外，算法将每一个节点的状态分为3类：未被遍历到的节点为new；在openList表中的为open；被移入到closeList表中的为closed。

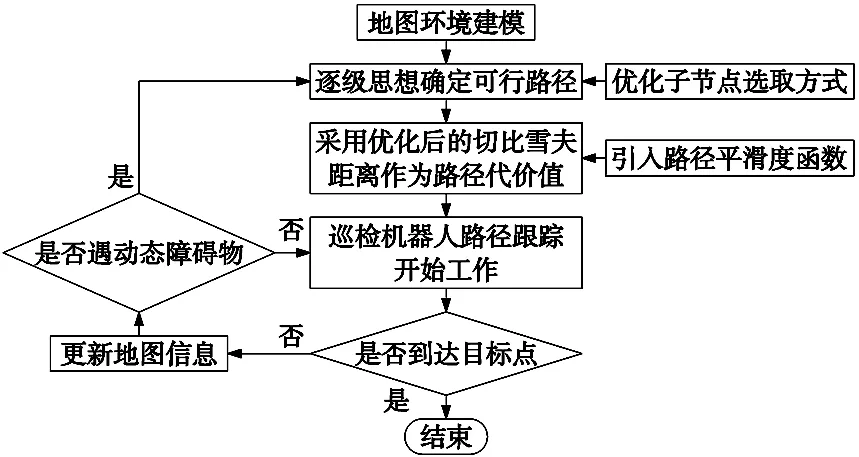
图2 改进D*算法流程图

1.2.2 D*算法流程

D*算法主要分为两个部分，第一部分为Process_state，是基于A*算法从目标点往起始点搜索，主要用于环境信息已知，障碍物为静态的路径规划；第二部分为Modify_cost，主要用于修正出现动态障碍物时导致代价值发生变化时的节点信息，属于动态避障搜索阶段。D*算法仿真结果如图1所示，图1a表示当障碍物为静态时，地图信息如同初始规划一样，即h(X)=k(X)；若在路径中遭遇动态障碍物为黑色栅格时，节点状态变为Raise态，灰色栅格为再规划路线，可以看到未受影响的节点仍在再规划路径中。

(a) 原始路径 (b) 遭遇动态障碍物时的路径

在图1中可以直观的看出，D*算法仅仅需要重新计算从当前节点到绕过动态障碍物的新路径，避免了回溯的高计算成本。然而D*算法是向周围8个子节点进行扩展搜索，忽略了动态障碍物导致最终路径存在的非必要转弯问题；使用欧式距离指标进行评价，在长度优先的前提下，会从两个障碍物之间穿过，对巡检过程中的安全性产生了一定的威胁。

2 D*算法改进

针对上述问题，本文对传统D*算法进行了改进：优化了子节点的选取方式，以局部环境关键节点为主，舍弃无用节点和危险节点；又改进了代价估计函数，针对传统的欧式距离作为代价值进行了修正，新增了平滑度函数对规划路线偏离理想路径的程度进行惩罚，避免巡检机器人在小范围区域内较高的转弯频率，以增加路径的平滑度。

2.1 节点选取的改进

在D*算法中，是以当前节点为基准，选择其8个邻近子节点完成扩展操作，由于使用欧氏距离作为代价的评估，易知在斜方向上代价值较低，这也就间接导致了路径会在两个障碍物之间穿过的情形，本文将子节点的选取分为两个级别：高级子节点和低级子节点，为避免穿过障碍物之间的狭缝，将如图3所示的水平竖直方向上的标识为(2,4,6,8)的子节点作为高级子节点，斜方向上的标识为(1,3,5,7)的子节点作为低级子节点；选用高级子节点作为首选扩展方向，并按照以下准则选用低级子节点：

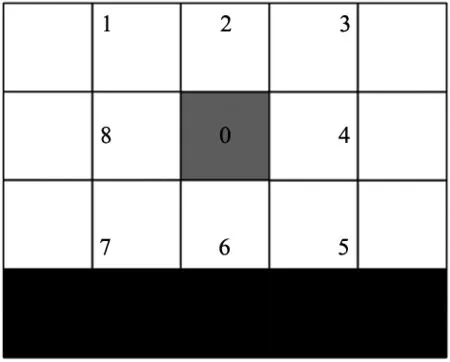
图3 子节点扩展

(1)若2为障碍物，禁选节点1、3。即不生成0-1、0-3路径。

(2)若4为障碍物，禁选节点3、5。即不生成0-3、0-5路径。

(3)若6为障碍物，禁选节点5、7。即不生成0-5、0-7路径。

(4)若8为障碍物，禁选节点7、1。即不生成0-7、0-1路径。

2.2 代价估计函数的改进

上文中提到，D*算法常用欧氏距离作为代价值。由式(2)可知，需要进行开方处理，降低了程序的运行速度，并且欧氏距离即为二维空间下两点间的直线距离，并未考虑到巡检机器人在运行过程中的角度信息，故而最终会规划出多次转弯的路径。

因此，本文首先对代价估计函数中代价值的选取做出优化，选用切比雪夫距离取代欧氏距离，在二维空间内，两个点(x1,y1)、(x2,y2)之间的切比雪夫距离的表达式如下：

dChebyshev=max||x2-x1|，|y2-y1||

(4)

本文在研究中设置垂直水平方向的代价值为10，对角线方向的代价值为14，对于使得路径产生不利拐角的最优节点，既人为增加其启发值，使得其变为次最优节点；又避免了开方运算，从而提高算法速度。此外，令：

hdiagonal=min(|x2-x1|,|y2-y1|)

(5)

hstraight=||x2-x1|-|y2-y1||

(6)

将代价值带入，可得到优化后的代价估计函数为：

h(n)=14min(|x2-x1|，|y2-y1|)+10||x2-x1|-|y2-y1||

(7)

2.3 平滑度函数的引入

本文在改进代价估计函数的基础上再引入平滑度函数f(θ)对规划路径偏离理想路径(初始点与目标点的直线)的程度进行惩罚，筛选出每一次扩展时偏移程度相对较小的路径，从而最大可能性上避免移动机器人的无效转弯。定义路径平滑度函数[12]如下：

(8)

式中，θ为待定子节点与父节点之间形成的路径与理想路径之间的夹角；μ为环境因子。

2.3.1 平滑度函数的分段

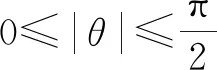
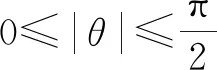
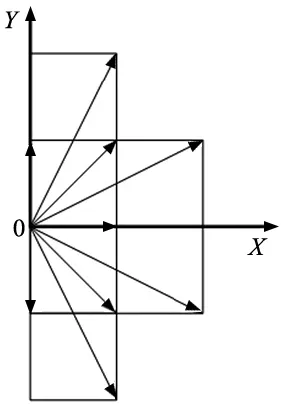
图4 路径移动方向

由图4可知，当路径为两个栅格的对角线时，存在4个代价值相同的子节点且关于X轴对称，因此须将X轴上2个子节点和X轴下2个子节点分开即可，故将θ平均分为3段。

2.3.2μ值的选取

μ值描述不同环境下障碍物对环境的影响，与障碍物所占环境地图面积比率直接相关[12]。在MATLAB代码中，随机生成的障碍物概率为20%～30%，结合实验与实践，本文取μ=2。

3 仿真结果与分析

3.1 仿真环境与测试对象

为了对改进后的D*算法的性能进行验证，对于传统的D*算法与改进后的D*算法进行对比仿真，算法代码在MATLAB R2019a平台进行编译。

建立不同尺寸的栅格地图模型，为了保证仿真实验结果的普遍性，避免特定环境带来的影响，采用不同数据在同一台计算机上分别进行多次仿真，分别建立不同尺寸的栅格地图，并随机生成静态和动态障碍物，并选取不同的障碍物覆盖率进行多次对比。

在实际仿真中，对同一障碍物覆盖率下的路径规划进行多次仿真，由于篇幅限制，本文只附上10×20的栅格地图环境下20%、25%、30%的障碍物覆盖率时的各一份对比仿真图。分别如图5～图7所示。

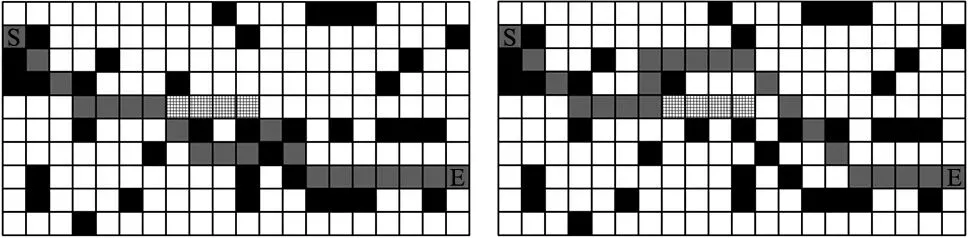
(a) 传统D*算法 (b) 改进D*算法

3.2 仿真结果分析

对于每种栅格地图，采用不同的障碍物覆盖率和障碍物分布，进行数十次的仿真并记录下所得路径的平均拐点数和算法平均规划时间，所得结果如表2和表3所示。

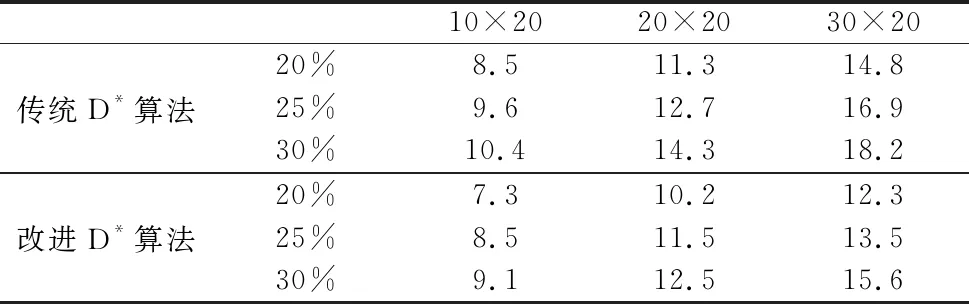
表2 不同环境下拐点数目

表3 不同环境下规划时间

由上述表格可知，改进后的D*算法相较于传统D*算法所规划的路径拐点数量更少，减少了约30%；可以在较小的迭代次数内获得最优解，从而使得规划时间更少，时间节约了约20%；在地图环境越复杂时，越能体现该算法的优越性。因此，本文建立的改进D*算法可有效地避免传统D*算法的转弯次数多的缺陷，并且提高了算法效率，规划所得路径也具有更高的安全性，有效提升了路径质量。