基于FAMVEMD和改进CYCBD的滚动轴承微弱故障诊断*

唐贵基，丁 傲,，王晓龙，张 晔，姜 超，李海明

(1.华北电力大学机械工程系，保定 071003；2.国网长春供电公司，长春 130021)

0 引言

滚动轴承广泛应用于工业生产领域，但其工作环境恶劣，易发生故障，为保证设备及人员安全，对滚动轴承进行早期故障诊断意义重大[1]。然而实际运行中所测早期故障信号非平稳、非线性、周期性冲击成分微弱，因此强噪声下提取轴承微弱故障特征一直是该领域的研究热点和难点[2]。

目前，常见的快速傅里叶变换、功率谱密度、经验模态分解、小波变换等特征提取算法均针对单变量信号，对多测点信号同步分析无能为力。多元经验模态分解(MVEMD)[3]可实现多元信息联合分解，但存在多通道相互干扰、各模态层间不连续等问题[4]。为此，基于阶数统计滤波器的快速自适应多元经验模态分解(FAMVEMD)被提出，目前该算法已应用于检测心脏瓣膜病变[5]，尚未在机械故障诊断领域应用。鉴于FAMVEMD的抗干扰能力强、计算速度快等优势，在此尝试将其应用于滚动轴承故障特征提取。

解卷积利用构造逆滤波器增强信号的冲击特征。最小熵解卷积(MED)采用峭度作为逆滤波器的目标函数，但其对周期性脉冲不敏感。最大相关峭度解卷积(MCKD)采用相关峭度度量周期性脉冲，然而强背景噪声下易引起相关峭度估计偏差，分析效果欠佳[6]。近年来，BUZZONI等[7]提出了循环平稳盲解卷积(CYCBD)，该算法以最大二阶循环平稳指标(ICS2)为目标函数，周期性故障特征提取能力优于MED和MCKD。目前CYCBD已用于诊断轴承、齿轮的故障损伤[8-10]，但存在以下不足：①ICS2仅对特定周期进行解卷积，循环频率设置的准确性严重影响解卷积效果；②滤波长度设置不当会影响故障特征增强的效果。针对该问题，本文提出基于多点峭度和自相关能量的改进CYCBD，可自适应选取循环频率和滤波长度，获得最佳解卷积分析结果。

鉴于上述分析，本文提出一种FAMVEMD和改进CYCBD相融合的故障诊断方法，对实验数据进行分析，可实现故障特征的精确提取。

1 基于FAMVEMD的多通道信号重构

1.1 FAMVEMD算法简介

Y(t)为一组p元信号，FAMVEMD算法步骤如下：

步骤3：找到投影信号pθk(t)的最大值和最小值；

步骤4：根据极值间距离，确定滤波器窗口大小；

步骤5：计算最大包络emax,i(t)、最小包络emin,i(t)和平均包络mi(t)，对各通道使用具有相同窗口大小的最大和最小阶数统计过滤器进行滤波处理；

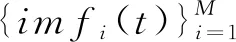
1.2 最优分量选择及多通道信号重构

在筛选最优IMF分量进行信号重构方面，互相关系数-峭度指标应用广泛[11]，但互相关系数的阈值依赖经验且易受噪声影响，而峭度指标易忽略幅值较大且具有分散分布的IMF[12]。为此，本文提出基于自相关能量-线性峭度的最优分量筛选和多通道信号重构。

(1)计算各IMFs归一化自相关能量。自相关函数具有优良的周期性成分检测能力和随机噪声消除能力，将自相关能量(AE)作为衡量周期性成分的新指标：

(1)

式中，Rimf(n)为IMF的自相关信号；AEimf为Rimf(n)的能量值。当IMF的时域波形中蕴涵的周期性冲击成分越多，则其自相关信号的能量值AEimf越大。

按照式(1)计算第j个通道的各IMFs的自相关能量AEj,i，则j通道归一化自相关能量G-AEj,i：

(2)

(2)计算各IMFs归一化线性峭度。线性峭度(L-kurtosis)可实现采样值线性组合的无偏估计，抗干扰能力和鲁棒性更强[13]。r阶随机变量X的线性矩为[14]：

(3)

式中，任意随机变量Xr-k:r的数学期望E[Xr-k:r]表示为：

(4)

线性峭度定义为2阶线性矩与4阶线性矩的比值：

(5)

按照式(5)计算第j个通道的各IMFs线性峭度指标Lkuj,i及本通道内线性峭度最大值maxLkuj和最小值minLkuj，得到归一化线性峭度G-Lkuj,i：

(6)

(3)计算各IMF分量的加权指标。将归一化线性峭度G-Lkuj,i和归一化自相关能量G-AEj,i相乘，得到第j个通道的各IMFs加权指标：

Wj,i=G-AEj,i·G-Lkuj,i

(7)

(4)筛选各通道最优分量。筛选出第j个通道的加权指标最大分量作为该通道的最优分量，记为IMFj,best。

(5)多通道信号重构。各通道最优分量携带的冲击特征的相对重要性存在差异，采用线性峭度作为权重指标衡量各分量的重要程度，进一步强化故障特征信息。p通道的最优分量在信号重构中的权重值为：

(8)

按照权重值得到重构信号为：

(9)

2 改进循环平稳盲解卷积算法

2.1 CYCBD算法简介

s为源信号，CYCBD通过构造逆滤波器h提取具有循环平稳特性的冲击成分，从观测信号x获得目标源信号s0。ICS2被定义为：

(10)

式中，H为矩阵的共轭转置；RXWX为加权相关矩阵；RXX为相关矩阵；U为加权矩阵，可表示为：

(11)

(12)

(13)

式中，N为源信号长度；L为滤波长度；k为样本数；Ts为故障周期。循环频率定义为a=k/Ts，fs为采样频率，tN-1为第N-1个数据对应的时间，则k(N-1)/Ts可改写为kfstN-1/Ts，当k=fs时，循环频率为故障特征频率。

2.2 基于多点峭度和自相关能量的CYCBD改进策略

CYCBD解卷积效果受循环频率a和滤波长度L影响，本文采用多点峭度选取a，应用自相关能量对L进行设置，实现CYCBD算法的改进，具体步骤如下：

步骤1：故障周期范围设定。根据轴承参数计算内圈、外圈、滚动体理论故障特征频率，由于实验及工程数据中测得转速存在误差，故将故障周期范围扩展为：

Trange.m=[Tfm-5,Tfm+5]

(14)

式中，Tfm=fs/fm为故障特征理论周期；fs为采样频率；fm为不同类型故障的理论故障特征频率，其中fi、fo、fb分别为内圈、外圈、滚动体的故障特征频率。

步骤2：循环频率选取。多点峭度定义如下：

(15)

式中，y为冲击信号；t为目标矢量，是一个以解卷积周期为间隔的脉冲序列向量，解卷积周期T=fs/fm；Ns为输入信号长度；步长设为0.1，在故障周期搜索范围内，计算输入信号多点峭度值，多点峭度最大值对应最优解卷积周期Tm，从而确定最优循环频率a=fs/Tm。

步骤3：滤波长度设置。滤波长度的寻优范围文献[15]设置为[20～200]，步长设置为1，计算不同L时的解卷积信号的自相关能量值，使用自相关能量作为衡量输出信号是否为具有周期冲击特性的判别依据，自相关能量最大时对应的L值作为最优滤波长度。

3 滚动轴承故障诊断流程

强噪声下轴承故障诊断多为单通道信号分析，易造成故障信息丢失，为此本文利用FAMVEMD和加权指标对多通道信号进行分解和重构，有效剔除噪声。将改进CYCBD作为后处理环节，自适应选取循环频率和滤波长度，进一步增强故障特征，诊断流程如图1所示，具体步骤如下：

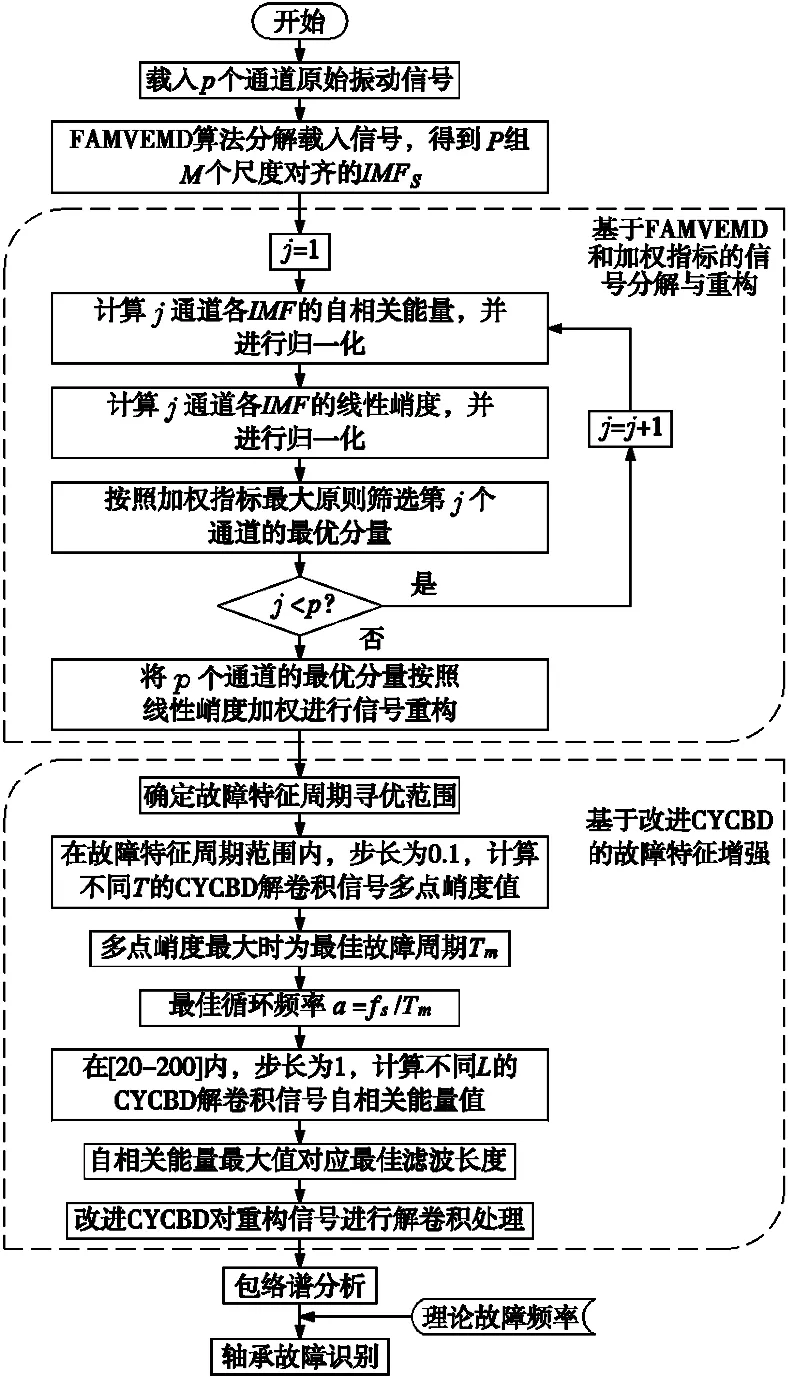
图1 滚动轴承故障诊断流程图

(1)应用FAMVEMD算法将p(p=1,2,…,j)个通道的故障振动信号分解为p组M个尺度对齐的IMFs；

(2)计算第j个通道内各IMF的自相关能量和线性峭度并进行归一化处理；

(3)按照式(7)计算各IMF的加权指标，按照加权指标最大原则筛选第j个通道的最优分量；

(4)将各通道最优分量作为源信号，按式(8)计算各最优分量权重，得到线性峭度加权的重构信号；

(5)根据滚动轴承理论故障特征频率计算故障特征寻优周期范围；

(6)在故障特征周期范围内，步长设为0.1，计算不同故障周期时的CYCBD解卷积信号的多点峭度值，多点峭度最大时的周期为最佳故障周期Tm，则最优循环频率a=fs/Tm；

(7)将重构信号作为CYCBD的输入信号，在[20～200]范围内，按步长为1，计算不同滤波长度时的自相关能量，自相关能量最大值对应最优滤波长度；

(8)根据寻优结果设置CYCBD参数，对重构信号进行解卷积处理，并计算解卷积信号的包络谱；

(9)滚动轴承理论故障特征频率值与包络谱中峰值明显的谱线进行对照，诊断故障类型。

4 实验验证

4.1 实验平台简介

采用如图2所示的旋转机械振动及故障模拟实验平台进行数据实测，使用SKF6025型轴承，轴承节径39.04 mm，滚动体直径7.94 mm，滚动体个数9个，接触角0°，局部微弱损伤深1.53 mm、宽0.2 m。主轴转速为1470 r/min，利用压电式加速度传感器同步采集3个通道数据，采样频率fs=12 800 Hz，转频fr=24.5 Hz。分析点数Ns=8192，外圈、内圈、滚动体的理论故障特征频率分别为fo=87.83 Hz、fi=132.67 Hz、fb=115.48 Hz。

图2 旋转机械实验平台

图3为实验信号波形及频谱，通道1和3的波形中存在明显冲击，但相邻冲击间隔非任障特征频率的倒数，通道2中仅有个别高幅值冲击，各通道包络谱中均未获取故障特征，传统包络分析无法甄别该轴承运行状态。

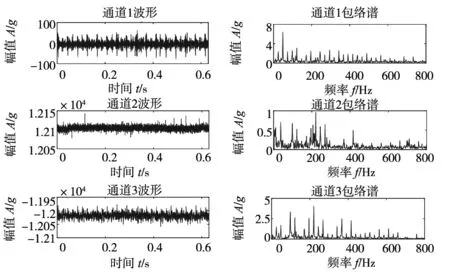
图3 各通道的实验信号时域波形及包络谱

4.2 实验信号分析

使用FAMVEMD对各通道信号进行分析处理，1、2、3通道各IMF的加权指标计算结果如图4a所示，选取1通道IMF2、2通道IMF4、3通道IMF4作为最优分量。将最优分量进行线性峭度加权，得到重构信号的波形如图4b所示。根据不同故障的理论特征频率，将理论周期搜寻区间设为：[140.7,150.7]、[91.5,101.5]、[105.8,115.8]。由图4c所示的多点峭度值随故障周期变化曲线可知，最优故障周期Tm为111.0，则CYCBD的循环频率a=fs/Tm=115.32。令a为115.32，不同L时的CYCBD解卷积信号自相关能量计算结果如图4d所示，可知最优滤波长度为105。使用改进CYCBD处理重构信号，如图4e的解卷积信号时域波形中可见脉冲峰值间隔约为0.08 s，与故障周期吻合。解卷积信号包络谱如图4f所示，图中fb及其2～6倍频处波形峰值突出，谱图清晰，干扰成分被有效剔除。由此表明：FAMVEMD与改进CYCBD相结合的方法能够准确提取故障特征，从而判断故障类型为滚动体故障。

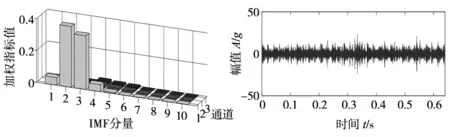
(a) 各通道IMFs加权指标值 (b) FAMVEMD重构信号的时域波形

4.3 算法对比分析

分别采用EEMD+CYCBD、FAMVEMD+快速谱峭度及FAMVEMD+MCKD等3种方法进行对比研究。

采用EEMD信号重构方法[16]处理多通道信号，使用CYCBD算法(a=115.32,L=105)分析重构信号，得到解卷积信号包络谱如图5a所示，可识别出fb和2倍频，幅值分别为0.113和0.084 1，未见3～6倍故障频率，杂频幅值较高，无法准确判断故障类型。

对FAMVEMD重构信号进行快速谱峭度分析，按分解级数为3.5、中心频率为800 Hz、带宽为533.33 Hz设定带通滤波器参数，所得滤波信号包络谱如图5b所示，fb及2倍频可被提取，但幅值较低，周边杂频生成较多。

采用MCKD对FAMVEMD重构信号进行解卷积处理，MCKD参数设置与改进CYCBD保持一致，解卷积信号包络谱如图5c所示，基频特征频率较为清晰，仍存在幅值较高的杂频，故障频率的倍频未见，且其基频幅值仅为本文所提方法拾取的基频幅值的37%。

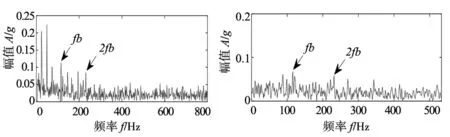
(a) EEMD+CYCBD (b) FAMVMED+快速谱峭度

综上所述，本文信号重构方法可有效提取故障信息，改进CYCBD在特征提取上优于快速谱峭度和MCKD。

5 结论

针对滚动轴承微弱故障识别问题，本文提出了基于FAMVEMD和改进CYCBD的诊断新方法，并通过实验信号进行验证，得到如下结论：

(1)采用自相关能量-线性峭度准则对多通道振动信号进行最佳本征模态分量筛选及信号重构，可有效实现干扰噪声剔除，对后续解卷积分析具有促进作用。

(2)按照多点峭度和自相关能量最大原则可自适应设置CYCBD循环频率及滤波长度参数，避免人为主观设置存在的弊端。应用改进CYCBD对多元重构信号进行解卷积处理，可实现轴承周期性冲击特征的进一步强化放大。

(3)实验信号的多方法对比验证结果表明，本文所提方法有更强的噪声抑制能力，在轴承微弱故障特征提取方面优势明显。