基于误差分离样本优化的主轴热误差建模研究*

张 蕾，黄美发，陈 琳

(1.玉林师范学院物理与电子信息学院，玉林 537000；2.桂林电子科技大学机电工程学院，桂林 541004；3.广西大学机械工程学院，南宁 530004)

0 引言

在加工过程中，数控机床的总误差主要由几何误差、力误差和热误差等组成，而因发热造成的热误差占比达70%左右[1]。在关键测温点优化方面，谢飞等[2]利用系统聚类和灰度关联对温度测点的优化进行了研究，使测量的温度变化值能有效地体现主轴热变化量。在热误差建模方面，先后建立了多种人工智能和机器学习预测模型，比如支持向量机(SVM)、模糊神经网络、深度学习、最小二乘支持向量机等[3-8]，有效利用机器学习的“黑箱”特性建立温度变化与热误差之间非线性的联系，但在变化的环境温度、工况条件和主轴转速下的建模研究较少，使得热误差补偿技术在实际加工中对误差的预测精度不高，泛化和推广能力较差。

针对不同转速对热误差的影响，提出一种基于误差分离样本优化的热误差建模方法，根据造成车床热误差变化的各项因素进行热误差分离，并将数据样本通过聚类分组和特征提取以进行优化，并以优化后的样本进行热误差建模。实验结果表明，经样本优化的热误差模型具有较好的预测精度。

1 机床热误差测量方案

以某型号数控车床作研究对象，其最大转速为1600 r/min。首先通过对数控车床进行热分析，并将10个关键测温点分别布置在车床主轴、电机和变速箱等位置，具体测温点布置如表1所示。将测量的温度数据，利用系统聚类的方法[2]优化测温点，并以测温点3、5、10的温度变化量θ3、θ5、θ10作为热误差建模的三个输入量。

表1 温度传感器布置

以主轴Z方向为例，实验采用电涡流位移传感器对主轴Z方向进行热变形采集，其分辨率为0.01 μm。设置电涡流位移传感器如图1所示。

图1 设置电涡流位移传感器

根据表2进行采集实验，从车床冷态分别以主轴转速从400 r/min～1400 r/min间隔200 r/min依次进行测量，每次系统采集热误差和温度值的时间间隔为2 min，采集时间为2 h，达到当前转速热平衡，共测到6组数据样本，数据样本的热误差变化如图2所示。为分析模型的预测性能，再测一组测试样本数据，由车床开机以转速500 r/min运行1 h再以1500 r/min运行1 h，得到K7样本数据。

表2 不同主轴转速和初始环境温度

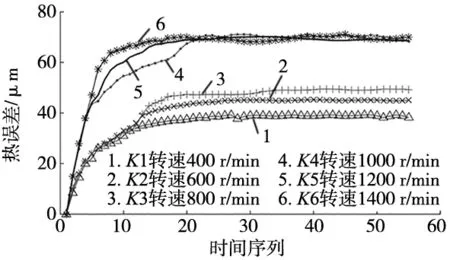
图2 6种不同转速的主轴热误差

由实验测量结果可以看出，该车床主轴转速在1000 r/min以下时，热平衡时的热变形因转速影响温度上升而上升。在1000 r/min以上时，车床达到最大转速热平衡，最大热变形维持在70 μm左右。

2 热误差分离及样本的优化

2.1 热误差分离

在实际加工过程中，除了主轴部件(电机、变速箱、主轴等)温升对机床热误差起主导作用外，环境温差、不同的主轴转速和机床工作状况等因素都会对热误差造成一定的影响，这里将主轴部件温升作为产生热误差的主要因素，环境温度、工作状况、转速等方面作为热误差的影响因素。而正是这些影响因素使得在温升作用下的热变形趋势产生一定波动，也是造成热误差模型的实际预测精度不高的原因之一。而在相对恒温的环境和单一工作状况下(环境温度变化在5 ℃内，即环境温度因素尽量减小的情况)，机床热变形的波动主要由转速的改变所影响。在此将热误差进行分离，随时序变化的热误差E(t)可以表示为：

E(t)=T(t)+S(t)+A(t)

(1)

式中，T(t)为由温升所引起的误差；S(t)为不同主轴转速所引起的误差；A(t)为其他因素引起的误差(包括环境温度变化等因素)。

由式(1)可知，当解得T(t)、S(t)和A(t)即可求得E(t)。而温升与主轴热误差的时序函数关系T(t)可通过线性回归或机器学习等方法建模拟合，主轴转速所引起的误差S(t)可通过多次测量不同主轴转速下温升与热误差的数值，将S(t)所造成的热误差波动通过机器学习“黑箱”模型进行反映。在本次实验中，A(t)已通过营造恒温环境和主轴空载等将其影响降低最小，同时特定条件下的其他因素A(t)也在热误差建模中通过训练样本进行了一定的反映。

数控机床在实际的生产与检测中，测量出全段主轴转速的温度与热误差数据是需要大量的人力物力以及时间成本的，也很难测量完成，比如为了更好提取不同转速的波动特征，设置测量转速间隔为50 r/min，则需要测量的样本批数为32批，样本量为1760个，数据量较大。而且测得的数据样本太多会在训练热误差模型环节造成一定影响，比如不同的机器学习建模所需的数据样本量有要求，有的只适合小样本学习，比如支持向量机。而可全样本建模的神经网络等方法也会因为样本特征不够明显，容易对一般样本细节过多的学习以致过拟合。所以，样本的优化与特征提取对模型的建立有重要作用。而对不同转速数据样本的波动特征进行提取，并以波动较明显的数据样本进行建模训练，使得训练后的模型在充分学习T(t)的情况下又包含S(t)的波动特征，也可避免出现过拟合现象。

2.2 样本优化

为使优化的样本特征更具典型化，将样本K1～K6中的热误差曲线进行聚类分析，并分为两组，分组如表3所示。

表3 样本聚类分组结果

优化数据样本，就是对S(t)影响较大的样本进行特征提取。假设T(t)为一条能反映温升与热误差变化趋势的光滑曲线，即T(t)可表示由温升所影响热误差的变化速率、滞后和最大值等，将K1～K6的样本点统一到相同坐标轴，采用多项式对每个样本数据进行拟合，即提取T(t)中热误差的变化趋势。其中，确定系数R2是以范围0～1的数据来表示拟合程度，R2越靠近1则说明拟合越好，这里将所有样本拟合结果的R2控制在0.98以上，最后计算出拟合曲线与实际数据误差的均方根，结果如表4所示。

表4 样本拟合确定系数与均方根误差

数据样本中均方根误差越大则说明样本受S(t)波动影响越大，由表4可知，K3、K4和K6的均方根误差大于1，而根据对样本聚类分组的结果，取第一组和第二组中均方根误差最大的样本，即样本K3和K4。

3 热误差的建模和比较分析

3.1 主轴热误差模型的选择

为更好地比较模型预测的性能，现测试单个训练样本下模型的预测能力，以K4作为训练样本，K3、K5作为测试样本，对小样本泛化能力较好的支持向量机(SVM)、高斯过程回归(GPR)、可用于大样本学习的BP神经网络(BP-NN)以及多元线性回归(MLR)进行建模比较。预测结果如图3、图4和表5所示。

(a) 预测值 (b) 预测残差

(a) 预测值 (b) 预测残差

表5 4种模型的均方根误差 (μm)

从图3、图4和表5可知，4种模型在以K4为训练样本进行建模后，对K5的测试样本的预测都表现良好，均方根误差都在2.5 μm以下，这是由于机床在1000 r/min和1200 r/min达到热平衡状态的最大热误差基本都在70 μm左右。而以K3作为测试样本时，机床800 r/min热平衡的最大热误差仅在45 μm左右，只有SVM和BP-NN模型可有效预测，均方根误差在3 μm左右，说明SVM和BP-NN可通过自身的“黑箱”特质很好地反映由温升所引起的误差T(t)。而高斯过程回归(GPR)和多元线性回归(MLR)的预测效果不理想，均方根误差分别达到8.00 μm和7.48 μm，对T(t)反映得不够。

在此，选择SVM和BP-NN对不同转速所造成的误差波动特征进行学习。

3.2 样本优化的热误差模型建立与预测结果分析

鉴于SVM的泛化能力较强，但不适合大样本学习，所以将SVM进行样本优化的建模，即以K3、K4作为训练样本进行建模。为了更好地比较模型预测效果，针对BP-NN可以对大样本进行学习使得样本中的各种特征均能得到一定反映的特点，将BP-NN进行全样本建模，即以K1、K2、K3、K4、K5、K6为训练样本进行建模。再以K4为单一训练样本的SVM模型作为比较，3个模型均以K7为测试样本，预测结果如图5、表6所示。

(a) 预测值 (b) 预测残差

表6 均方根误差与最大残差 (μm)

由图5和表6可得，单样本SVM只依靠自身的泛化能力，将K4单一主轴转速的数据进行学习预测，对不同主轴转速的波动特征缺少学习，使得预测精度略低。全样本的BP神经网络虽然可以学习所有样本的波动特征，但因样本特征不够典型，造成过多学习一般样本细节，而导致预测结果不理想，最大残差达到9.51 μm。而经样本优化的SVM即能在一定程度上学习不同转速波动特征，又可避免样本过多而导致模型复杂失效，预测结果的均方根误差2.89 μm，最大残差5.29 μm，具有较高的预测精度。

4 结论

以某种通用的数控车床进行热误差补偿研究，通过实验采集7种不同主轴转速的温度与热变形量，并对样本数据进行误差分离与样本优化，建立样本优化的主轴热误差模型，经实验对比，得到如下结论：

(1)不同转速影响下的机床热源造成温升的不同，而通过测温点对温升的测量，再结合神经网络或机器学习自身的“黑箱”特质，可使建立的模型对由温度变化所引起的热误差T(t)进行有效地反映。

(2)除了优化机器学习自身性能的建模方法外，对数据样本的特征提取和优化也具有提高热误差模型预测精度的作用。

(3)针对不同主轴转速所造成的热误差波动S(t)，通过对数据样本的聚类分组、特征提取和样本优化，建立经样本优化的SVM热误差模型，并测试样本K7。预测结果为均方根误差2.89 μm，最大残差为5.29 μm，优于单样本SVM和全样本BP-NN。说明样本优化的SVM热误差模型在不同的主轴转速中具有较好的预测精度。