强力剐齿主轴变形对加工精度的影响分析*

赵彬彬，陈复兴，洪荣晶

(南京工业大学a.机械与动力工程学院;b.江苏省工业装备数字制造及控制技术重点实验室，南京 211800)

0 引言

强力剐齿又叫强力刮齿、车齿，是一种新的圆柱齿轮加工方法，可用于非贯通、无退刀槽内齿轮以及外齿轮加工[1]。这种方法基于齿轮啮合原理，结合了滚齿和插齿运动，可实现高速、高精度的切齿加工[2]。在刮齿领域，国内外学者在刮齿加工原理、数学模型建立、切屑成型机理、刮齿刀设计等方面取得了一些突破性进展，但对刮齿误差分析及补偿方面的研究有所欠缺。GUO等[3-4]分析了刮齿刀固有误差、刀具刃磨次数及刀具偏心误差对齿形精度的影响。郭二廓等[5-9]探索了刮齿加工切削机理，建立了强力刮齿的数学模型，研究了机床调整参数误差对齿形误差的影响，使用误差敏感系数矩阵进行误差补偿，并分析了加工工艺参数对齿向误差的影响，以及刀具和工件位姿误差对齿形精度的影响。杨亚蒙等[10]分析了各项几何位姿误差对法向齿廓误差的影响，并基于实际逆向运动学方法对误差进行了修正。吴震宇等[11]分析了轴交角误差对内齿轮刮齿加工精度的影响。以上学者主要研究了刀具和机床几何误差对刮齿加工精度的影响，但对强力剐齿力致变形误差方面研究较少。强力剐齿是多切削刃同时高速切削，切削力形成复杂，力致变形误差不容忽视，因此研究切削力致变形误差对剐齿加工精度的影响具有重要意义。

力致误差分析大多应用在车削、铣削及滚齿等传统加工工艺。YUE等[12]研究了由切削力引起的刀具偏转导致角铣削过程中的尺寸不精确和轮廓误差，并对误差进行了补偿。WANG等[13]研究了滚削力对主轴变形的影响。朱朝宽等[14]计算了滚削力，并研究了滚齿刀具变形对齿轮加工误差的影响。孙守利[15]研究了滚齿切削力对齿轮几何误差的影响，使用改进的粒子群算法优化了工艺参数。DENG等[16]提出了一种适用于高速干式滚齿机的力致误差模型，并对齿轮齿厚误差进行了补偿。

为分析力致变形误差对剐齿加工精度的影响，本文对切削力导致的主轴变形进行研究，建立主轴剐削变形模型，分析了主轴变形对中心距误差和轴交角误差的影响。基于齐次坐标变换理论和剐齿加工原理，建立强力剐齿的直接力致误差模型和齿轮法向齿廓误差模型。分析了中心距误差、轴交角误差和主轴变形方向对齿轮法向齿廓误差的影响。

1 剐齿加工运动学模型

根据强力剐齿加工原理，建立如图1所示的剐齿加工坐标系。

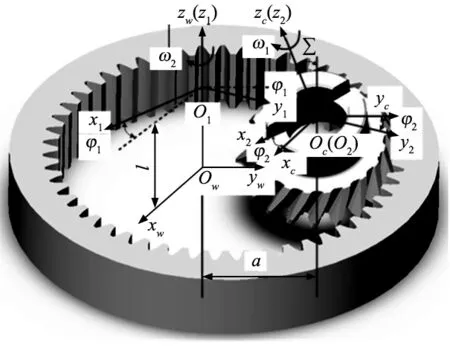
图1 剐齿加工坐标系

图中Sc(oc-xcyczc)和Sw(ow-xwywzw)分别为刀具固定坐标系和工件固定坐标系，xc轴和xw轴重合，两坐标原点的距离等于中心距a，zc轴和zw轴之间的夹角为∑。S1(o1-x1y1z1)和S2(o2-x2y2z2)分别固连于工件和刀具，随着工件和刀具的运动而变化，它们的初始位置分别于Sw和Sc重合。刀具的角速度为ω1，并且绕zc轴旋转φ2，轴向进给速度为v1。工件的角速度为ω2，绕zw轴旋转φ1，同时以速度v2沿着zw轴移动l。

图中，∑为轴交角，即刀具轴线与工件轴线的夹角。

∑=|β1±β2|

(1)

式中，β1为刀具的螺旋角；β2为工件的螺旋角。当剐削内齿轮时，“+”用于刀具与工件的旋向相反，“-”用于旋向相同；剐削外齿轮时，“+”用于刀具与工件旋向相同，“-”用于旋向相反。

刀具与工件之间的中心距a为：

(2)

式中，mn为工件的法向模数；z1为刀具齿数；z2为工件齿数；“+”用于剐削外齿轮；“-”用于剐削内齿轮。

剐齿加工过程可分为两个旋转运动和一个直线进给运动。轴向进给速度打破了刀具与工件成比例的运动关系，为保证齿形的正确加工，需要在刀具或工件原有转动的基础上添加附加转动。

当刀具附加转动时，附加的转动变化量为：

(3)

则附加转动后刀具的角速度为：

(4)

工件附加转动时，附加的转动变化量为：

(5)

则附加转动后工件的角速度为：

(6)

2 剐齿加工主轴变形分析

2.1 剐齿切削力计算

基于剐齿加工原理，LI、胡覃等[17-18]提出了一种剐齿微段刃模型。当刀齿逆时针旋转时，用Ⅰ表示切入刃，Ⅱ表示顶刃，Ⅲ表示切出刃。分别把切入刃、顶刃和切出刃分成m个微段刃，微段刃模型如图2所示。

图2 微段刃模型

根据金属切削原理，基于能量法得到剐齿加工切削力的计算方法为：

(7)

2.2 剐齿加工主轴变形模型

切削力导致工艺系统发生变形，最终影响剐齿加工精度。如图3所示为剐齿加工示意图。

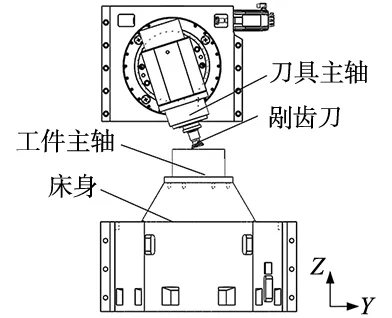
图3 剐齿加工示意图

根据刀具主轴和工件主轴在加工时的受力特点，将其简化成直线轴悬臂梁，如图4所示。

(a) 工件主轴 (b) 刀具主轴

图4a为刀具主轴简化示意图，l1为刀具主轴下端A到主轴固定端B的距离。以X方向受力为例，根据材料力学中梁弯曲变形理论，可以得到刀具主轴受到X方向切削力Fxt时的最大弯曲变形为：

(8)

式中，E1为刀具主轴材料弹性模量，N/mm2；d1为刀具主轴直径，mm。

同样的，如图4b所示，根据材料力学中梁弯曲变形理论，可以得到工件主轴受到X方向切削力Fxw时的最大弯曲变形为：

(9)

式中，E2为工件主轴材料弹性模量，N/mm2；d2为工件主轴直径，mm。

在剐齿加工过程中，刀具主轴和工件主轴的弯曲变形会使中心距发生变化，主轴中心距作为剐齿加工中的重要参数，将直接影响加工精度。作用在剐齿刀上的切削力Fxt和工件上的切削力Fxw是一对作用力与反作用力，在剐削外齿轮时，刀具主轴沿X正方向弯曲，工件主轴沿X负方向弯曲，如图5a所示，最终导致中心距增大；而剐削内齿轮时，刀具主轴沿X负方向弯曲，工件主轴沿X正方向弯曲，最终导致中心距减小，如图5b所示。则主轴中心距的变化量为：

(a) 剐削外齿轮 (b) 剐削内齿轮

Δa=|Δl1max|+|Δl2max|

(10)

则实际中心距为：

a′=a±Δa

(11)

式中，“+”用于外齿轮剐齿加工；“-”用于内齿轮剐齿加工。

刀具主轴和工件主轴的受力变形，还会引起轴交角的变化。如图6a所示，刀具主轴在受到Z方向切削力Fzt和Y方向切削力Fyt作用时，使A端产生转角误差Δ∑t，根据材料力学中梁弯曲变形理论，刀具主轴A端产生的最大转角为：

(12)

同理，如图6b所示，工件主轴受到Y方向切削力Fyw，则工件主轴C端产生的最大转角为：

(13)

如图6c所示，则轴交角误差为：

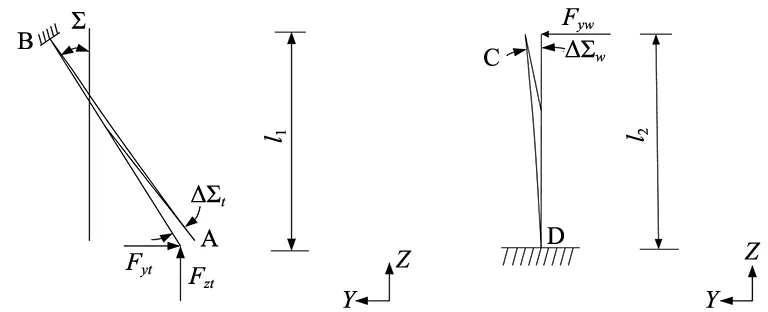
(a) 刀具主轴转角误差 (b) 工件主轴转角误差

Δ∑=Δ∑t-Δ∑w

(14)

则实际轴交角为：

∑′=∑+Δ∑=∑+(Δ∑t-Δ∑w)

(15)

通过剐齿切削力计算方法和主轴变形模型，得到中心距误差和轴交角误差与进给量、背吃刀量的关系，分别如图7和图8所示。

图7 中心距误差与进给量、背吃刀量关系 图8 轴交角误差与进给量、背吃刀量关系

从图7可知，中心距误差随着背吃刀量和进给量的增大而增大，但进给量对于中心距误差的影响要大于背吃刀量。由图8可知，轴交角误差随着进给量和背吃刀量的增大而增大，但轴交角误差对背吃刀量的变化较为敏感，随其增大而显著增大，而对进给量的变化不敏感。

3 主轴变形对加工精度的影响分析

3.1 力致误差模型

根据多体系统运动学理论，刚体Bi与相邻的刚体Bj之间的位置关系可以用齐次坐标变换矩阵表示。如图9所示，分别在刚体Bi与刚体Bj上建立笛卡尔坐标系，其中α、β和γ分别为绕x、y和z轴的旋转角；dx、dy和dz分别代表沿x、y和z轴的位移，因此，刚体Bj到刚体Bi的齐次坐标变换矩阵可表示为：

图9 相邻体相对运动示意图 图10 剐齿机床示意图

(16)

式中，Tx、Ty、Tz分别为沿x、y和z轴的平移运动变换矩阵；Rx、Ry、Rz分别为绕x、y和z轴的旋转运动变换阵。

图10为剐齿机床示意图，以床身为参考，将机床分为刀具端运动链‘0-1-2-3-4-5-6’和工件端运动链‘0-8-7’。

如图11所示为机床无误差运动传动链，利用齐次坐标变换理论，分析刀具端运动链和工件端运动链之间的位置和方向关系。

图11 剐齿机床无误差运动传动链

建立剐齿刀与工件的位置和方向关系，在坐标系6中，剐齿刀上的切削点定义为H6=(x6,y6,z6,1)T，而工件上的切削点在坐标系7中表示为P7=(x7,y7,z7,1)T。那么，在固定参考坐标系0中H6和P7的坐标可表示为：

H0=M06H6=Tx(X)Tz(Z)Ty(Y)
Ty(L)Rx(A)Ry(B)Ty(-L)H6

(17)

P0=M07P7=Rz(C)P7

(18)

式中，X、Y、Z、A、B、C分别为对应轴的运动量；L为刀具坐标系原点与A轴坐标系原点之间的距离。

因此，由工件坐标系到刀具坐标系的齐次坐标变换矩阵为：

M76=(Rz(C))-1Tx(X)Tz(Z)Ty(Y)
Ty(L)Rx(A)Ry(B)Ty(-L)

(19)

在剐齿加工过程中，切削力致工艺系统的变形会使各部件发生位姿偏差，因此，相邻部件之间位姿偏差变换矩阵为：

(20)

式中，Δα、Δβ和Δγ分别为绕x、y和z轴的旋转角误差；Δdx、Δdy和Δdz分别为沿x、y和z轴的直线位移误差。

剐齿切削力使各部件位姿发生偏差，最终导致刀具和工件的位姿发生改变，影响加工精度。因此建立一种直接力致误差模型，该模型考虑由力致变形最终导致的刀具位姿偏差和工件位姿偏差。如图12所示为有误差运动传动链，则在固定参考坐标系0中H6和P7的实际坐标分别为：

图12 剐齿机床有误差运动传动链 图13 法向齿廓误差模型

H0′=E06M06H6=EtTx(X)Tz(Z)Ty(Y)
Ty(L)Rx(A)Ry(B)Ty(-L)H6

(21)

P0′=E07M07P7=EgRz(C)P7

(22)

那么，由工件坐标系到刀具坐标系的实际齐次坐标变换矩阵为：

M76′=(E07M07)-1E06M06=(EgRz(C))-1EtTx(X)

Tz(Z)Ty(Y)Ty(L)Rx(A)Ry(B)Ty(-L)

(23)

式中，Et、Eg分别为刀具和工件的误差坐标变换矩阵。

设在刀具坐标系S2下的剐齿刀齿形方程为：

r(1)(u,θ)=x1(u,θ)i+y1(u,θ)j

(24)

式中，x1、y1为刀具齿形上的坐标点；u、θ为齿形的两个参数。

则工件的实际齿形方程为：

r(2)(u2,θ2)=M76′r(1)(u1,θ1)

(25)

剐齿切削力致工艺系统变形导致刀具和工件的位姿发生改变，使加工出的齿廓偏离理论齿廓，影响加工精度。为了分析力致变形误差对齿轮法向齿廓误差的影响，建立法向齿廓误差模型，如图13所示。

图13中，Q′为实际齿廓上的一点，过点Q′做基圆的切线，交于点T，Q点为理论齿廓上一点；u为渐开线展角；rb为基圆半径；σ0为基圆齿槽半角；QT为渐开线的展开长度；x′、y′为Q′点的坐标；f为齿廓任意一点处的法向误差值，则法向误差f为：

(26)

3.2 力致变形误差分析

基于剐齿加工原理和力致误差模型，以圆柱内齿轮剐齿加工为例。具体参数如下：刀具模数为3 mm，齿数为23，螺旋角为20°，工件齿数为63，压力角为20°，齿宽为50 mm，轴交角为20°，得到剐齿刀包络出的内齿齿形，如图14所示。提取包络出的齿形，根据法向齿廓误差模型，进一步得到中心距误差为0.1 mm的实际齿形和轴交角误差为0.01°的实际齿形，如图15所示。从图15中可以看出，中心距误差导致切削加工中齿轮左右齿廓欠切，而轴交角误差导致切削加工中齿轮左齿廓过切，右齿廓欠切。如图16所示为中心距误差和轴交角误差导致的法向误差，从图中可以看出，中心距误差导致左右齿廓的法向误差相同，而轴交角误差导致右齿廓的法向误差大于左齿廓。如图17所示为最大法向误差与中心距误差、轴交角误差的关系，由图中可知，左右齿廓的最大法向误差分别随中心距误差和轴交角误差的增大而增大。

图14 包络出的内齿齿形

(a) 中心距误差 (b) 轴交角误差

(a) 中心距误差 (b) 轴交角误差

(a) 中心距误差 (b) 轴交角误差

进一步分析不同方向力致主轴变形对剐齿加工精度的影响，以切削力为2193 N(背吃刀量为0.2 mm，进给量为0.1 mm/r)为例，如图18所示。从图中可以看出，X方向变形对法向齿廓误差的影响要大于Y方向。X方向变形导致中心距变化，因此X方向变形引起的左右齿廓的法向误差相同。Y方向变形对法向误差的影响很小。另外可以看出，Z方向变形导致的法向误差与理论误差相同，因此可知，Z方向变形不影响法向齿廓误差。

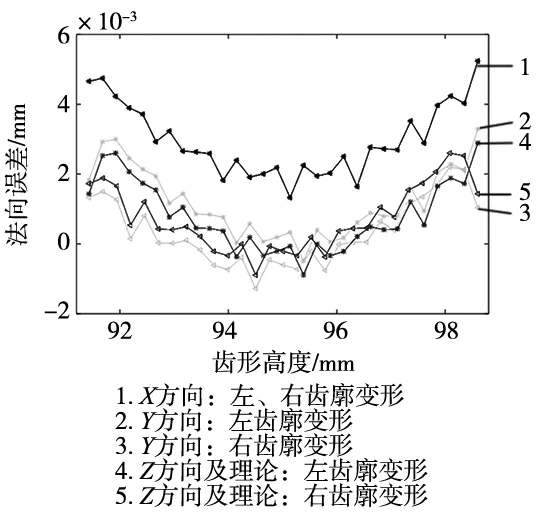
图18 不同方向变形对法向误差的影响

4 结论

(1)通过建立剐齿加工主轴变形模型，分析了主轴变形对中心距和轴交角的影响情况。其中轴角随主轴的变形而增大，中心距在剐削外齿时随主轴的变形而增大，在剐削内齿时减小。

(2)根据剐齿切削力计算方法和主轴变形模型的分析可知，中心距误差和轴交角误差随着背吃刀量和进给量的增大而增大。其中，中心距误差对进给量的变化更为敏感，轴交角误差对背吃刀量的变化更为敏感。

(3)通过建立力致误差模型和齿轮法向齿廓误差模型，分析了法向误差与中心距误差、轴交角误差及主轴不同方向变形的关系。其中，中心距误差会导致齿轮左右齿廓欠切，左右齿廓的法向误差相同；轴交角误差会导致左齿廓过切，右齿廓欠切，右齿廓的法向误差大于左齿廓。主轴X方向变形对法向误差的影响要大于Y方向，主轴Z方向变形对法向误差没有影响。