分数阶Lorenz系统和SIR传染病模型的数值模拟

雷俊磊，徐 玲，曾昌玺，高方启

（贵州师范大学数学科学学院,贵阳 550025）

混沌现象是E.N.Lorenz在简单数学模型中发现的，其既非周期又不收敛，并且具有一定的初值敏感性。对混沌系统现象理论进行研究可以通过Lorenz系统入手，目前在国内已有许多专家学者对其理论进行了深入研究，使其在许多相关学科包括数学、经济学、生物学等领域中都已经得到了广泛的应用。另一方面，传染病模型研究对于各类传染病的有效防控有着重要意义，已有许多学者对其性质、稳定性做了分析，而SIR模型是传染病模型中最经典的模型，适用于研究患者康复后不再被感染的传染病。

在众多学者中，周围[1]等详细分析了基于Grünwald-Letnikov定义的分数阶简化 Lorenz系统的FPGA实现结构，徐宝春[2]给出了提前和延迟管控隔离对香港SARS疫情的总体影响分析，徐英、杨娟[3]等分析了HIV/AIDS传播的动力学模型，霍静静[4]基于分数阶微分方程对两类分数阶模型的动力学行为特性进行研究，徐鸿鹏等[5]给出了一个新型的五维超混沌类Lorenz系统及其特性，并利用数值模拟进行了验证，刘向虎等[6]分析了一类带有不确定扰动的分数阶P型迭代算法。但他们都没有对整数阶到分数阶变化的Lorenz系统以及SIR模型进行分析，为探寻阶数变化对系统所带来的影响，本文借鉴了程全发等[7-9]对一类分数阶微分方程的算法分析，主要是对三维分数阶Lorenz系统和SIR传染病模型做了较为详细的分析。

1 预备知识

2.1 简化Lorenz分数阶混沌系统及其吸引子

取 h=0.001s，a=5，初值为(1，2，3)时，由模型(12)可以得到该系统的吸引子轨线相图如图1所示。

图1 分别为Lorenz系统的吸引子及其在各平面的投影图.

可以得出此时系统是混沌的。

2.2 q对系统的影响

由于当a=5，q=0.98时该系统能够产生混沌现象，现为探讨阶数q能否影响系统混沌现象的产生，取定 a=5，取阶数 q=0.50、0.65、0.80、0.90、0.93、1 时系统在x-z平面轨线的相图如图2所示。

图2 系统在不同阶数下x-z平面轨线的相图

由图2知，在(0，1]范围内，系统产生混沌的趋势随阶数增加逐渐明显，且阶数在(0.90，0.93]范围内存在一个使系统产生混沌的界点。

进一步探索该系统产生混沌时阶数的确定取值。同样取定参数a=5，取阶数q=0.90、0.91、0.92、0.95、0.98、1时系统在x-z平面轨线的相图如图3所示。

图3 系统在不同阶数下x-z平面轨线的相图

由图3可以得出当q=0.92时该系统开始产生混沌现象，若q=0.92是混沌产生的界点，可以通过Lyapounov指数去刻画，限于篇幅，本文不作详细论述。

3 SIR模型

图5 SIR模型

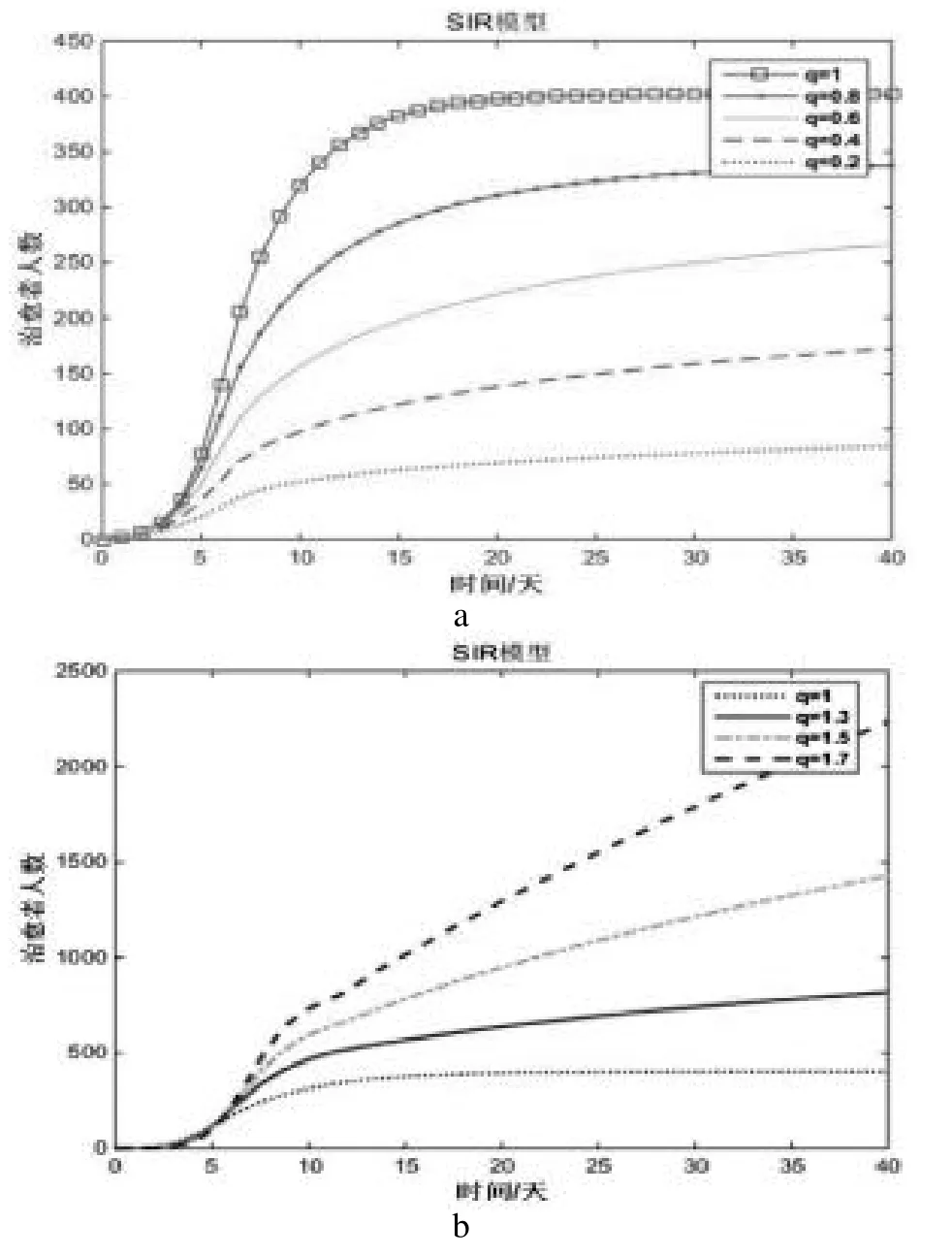
图6 阶数变化时治愈者人数的轨线图a;b

通过数值模拟发现阶数从 q=1均匀递减过程中，治愈者人数明显不断降低，并逐步趋向于平衡，当q=0.2时，在40天内治愈者人数始终低于100人，死亡率较高，传染病难以控制；阶数从q=1均匀递增的过程中，治愈者人数显著增加，在q=1.7时，治愈者人数随时间的增加近似呈直线增长，且增长速度较快，在40天内治愈者人数已超过2000人，利于传染病的控制。

4 结论

针对简化Lorenz分数阶混沌系统，通过MATLAB仿真分析了系统阶数变化对系统产生的影响，发现阶数的选取对系统混沌现象的产生有着重要作用。此外，本文对SIR传染病模型进行从整数阶到分数阶变化的研究发现，在一定范围内治愈者人数会随阶数的增加而增加，这对医学上更好地修正治疗方法或者方案进行对传染病的防治具有一定的启示意义。