管内插板后稳动态流动规律研究

2022-06-24刘阳陈杰黄国平

机械制造与自动化 2022年3期

刘阳，陈杰，黄国平

(南京航空航天大学能源与动力学院，江苏南京 210016)

0 引言

进气道与发动机相容性评定是现代喷气式发动机研制的一项重要科目，其中必要的内容之一是发动机的稳定性测试。在发动机实际使用过程中，飞机的机动、进气道内流动分离和地面涡吸入等原因会导致发动机和进气道的气动交界面(aerodynamic interface plane，AIP)处流动参数分布不均匀，而管道截面上的总压分布不均匀会对发动机运行的稳定裕度产生明显影响[1-2]，进而影响飞行安全。所以，在发动机地面试车时，会使用畸变发生装置模拟飞行条件下所存在的总压分布不均匀的畸变来流以测试发动机稳定性[3-4]。

插板式畸变发生器作为一种标准畸变发生装置[5]，广泛用于军用和民用喷气发动机的稳定性测试。插板式畸变发生器是利用管道内的挡板在其下游产生局部的总压损失，以便在管道截面生成类似于实际情况的稳态不均匀总压分布，并且管内的钝体绕流还会使得总压产生随时间的快速变化，这也是发动机实际使用中会面临的总压动态畸变。

在使用过程中插板高度和进气流量变化都会对AIP截面的稳动态畸变指数产生明显影响。为了更有效地预测畸变指数就需要详细了解插板后的流动结构，使用数值计算方法能获得丰富的流场信息，更详细地了解管道内插板绕流的流动结构。

现阶段有多种有效的数值模拟方法，RANS方法应用非常广泛，但对钝体绕流的流动情况预测不够准确，故本文使用一种混合RANS/LES方法对管道内插板绕流进行数值模拟。在混合RANS/LES模型中，通过使用RANS方法求解附面层和小分离区，降低LES模型中附面层位置的网格要求，并增大求解时间步长，以减少计算资源消耗。目前常用的分离涡模拟(DES)中附面层网格细化导致附面层计算域过早地由RANS方法切换到LES方法，进而产生网格诱导分离问题[6]，随后发展的延迟分离涡模拟(DDES)一定程度上解决了上述问题[7-8]，由MENTER F[9]提出的应力混合涡模拟(SBES)，对附面层RANS计算域有较强保护，并且能够更快地在不同计算域之间进行切换。

本文将使用混合RANS/LES的SBES方法对不同插板高度的管道几何模型内流动进行数值仿真，以探究插板后流动结构的沿程发展规律以及插板高度、进口马赫数对插板后沿程稳动态畸变发展的影响规律。

1 数值仿真方法及畸变指数

1.1 数值计算方法验证

本文所研究的流道结构示意图如图1所示。管道直径为D=905 mm。为保证插板前管道内边界层充分发展，设计插板前至管道进口的长度为2D；在实际实验设备中插板与发动机进口的轴向距离通常为3～4倍管径以保证发动机进口在回流区之后，故仿真中设计插板后至管道出口的长度为3.5D，并在出口后外接长度为2.5D的延长段以提高计算的稳定性。计算域全局采用结构化网格，如图2(a)所示，插板前后管道区使用碟形网格结构；如图2(b)所示，插板附近区域使用C型结构划分，以便于进行边界层加密，总网格数约为600万。

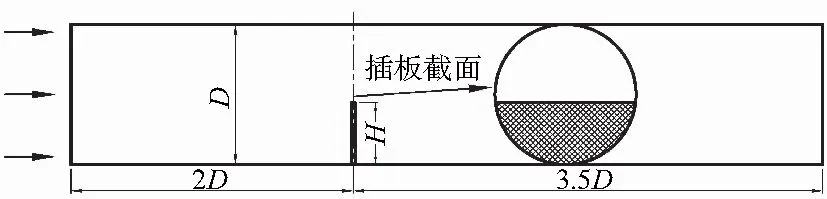
图1 计算模型

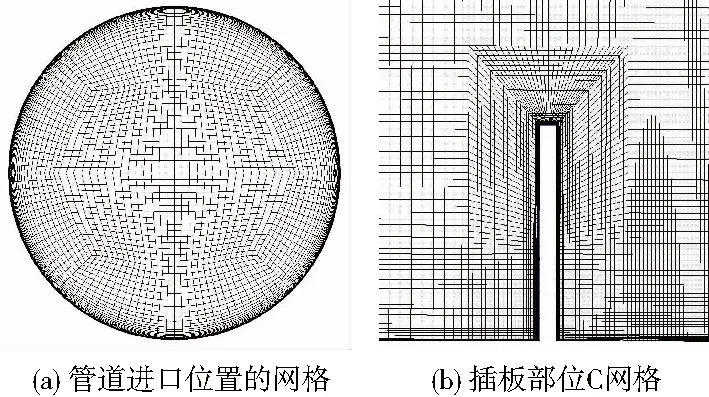
图2 插板网格划分

本文采用Ansys CFX进行流场的数值模拟，计算工质为理想空气，进口给定总温T*=288.15 K，总压P*=101 325 Pa；出口给定静压，通过调节出口静压实现不同进口马赫数工况的计算；对流项采用有界中心差分格式。定义气流通过时间为T=l/v，其中l为计算域长度，v为平均进口流速；计算时使用定常计算结果作为初场，经过2.5～3.5T后开始统计流场数据，统计时间约为10T。设置非定常时间步长时，保证CFL约为1。

江勇等[10]对插板式畸变发生器进行了实验研究，实验中使用了实际发动机在管道出口进行抽吸，通过调节发动机转速来调整管道内空气流量，使用总压耙测量了距离插板为3D位置的发动机进口处时均总压。为验证数值仿真的准确性，本文提取了与实验相同测点位置的仿真总压数据，并将二者数据进行了对比。

图3为数值模拟所得低压区平均总压与面平均总压的比值与实验数据对比；插板相对高度H是实际高度与管道直径的比值，折合流量由小到大依次对应的插板相对高度分别为36%、28%、20%。可以发现计算结果与实验测量值的变化趋势基本吻合，可以认为本研究中的网格划分方法以及计算设置满足研究要求。但计算与实验结果的误差有随着插板高度增加逐渐增大的趋势，最大误差约为5.8%。这可能是由于实验中测量面与发动机风扇距离较近，随着插板高度增加发动机对测量面影响逐渐增强而导致的。

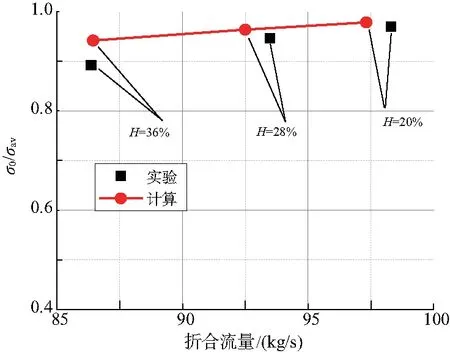
图3 计算结果与实验值对比

1.2 畸变指数定义

分析插板后流动的畸变程度时，常用的稳态周向畸变指数Δσ0作为稳态畸变指数，面平均紊流度εav作为动态畸变指数。

(1)

式中：σ0为低压区平均总压恢复系数；σav为测量面平均总压恢复系数。总压恢复系数是当地总压与管道进口平均总压的比值。

截面单个测点的紊流度为

(2)

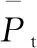
2 计算结果及分析

2.1 插板后主要流动结构分析

不同插板高度和进口马赫数工况下，插板前后流动结构基本相同，本文使用图4中进口马赫数Main=0.347、H=36%时管道对称面的时均马赫数云图和面流线图进行说明。可以看到由于插板存在对上游气流的影响，插板前有效流通面积会逐渐减小，气流逐渐加速。气流在插板上游表面形成滞止点，滞止点上部气流向上流动绕过插板，滞止点下部气流在插板与管壁交界的角区形成旋涡结构。气流在绕过插板时会产生向上的速度分量，流过插板后仍将继续有向上速度分量，导致流通面积最小处并不在插板位置，而在更下游的位置。

图4 管道对称面时均马赫数云图和流线图(Main=0.347，H=36%)

插板下游气流可以分为插板上部的高速区和插板后低速区两部分，两区之间存在有较大速度梯度的过渡区。低速区上部气体由于受到过渡区内剪切力作用，导致插板后形成了一个较大的回流区。观察经过插板上边缘位置流线可以看到，插板下游高速区的流通面积有先减小后逐渐增大的变化过程，即插板下游存在气动喉道，这就使得在进口马赫数足够大时，插板下游能够存在超声速区。

图5为进口马赫数Main=0.347、H=36%时插板下游沿程过流截面上的面流线及法向速度云图，4个截面与插板轴向距离依次为0.5D、1.5D、2.5D和3.5D。其中可以看到图4中插板前涡区的三维结构，插板前滞止点下部气流向下运动在角区形成涡结构，涡沿着插板前表面与管壁形成的圆弧角区向两侧运动，并在插板上表面与管壁形成的角区后产生两个较大的角涡，其影响距离较远，能够一直延伸到管道出口位置；同时每个角涡下部会形成一个方向相反的次涡。插板下游的角涡以及其下部的次涡构成了板后二次流的主要流动结构，由于涡结构的存在，导致管道中间部位的流体会从高速区向低速区流动，靠近管道壁面位置的流体会从低速区向高速区流动。

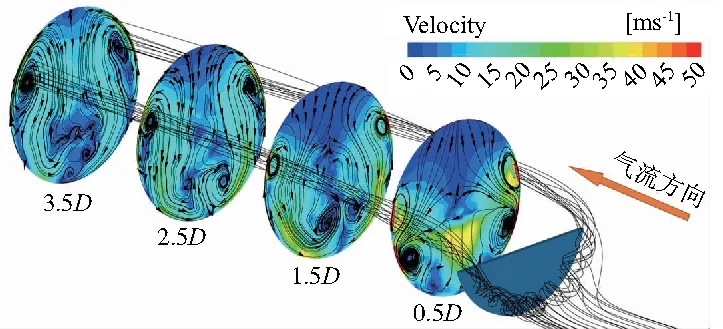
图5 插板下游面流线及其法向速度云图(Main=0.347，H=36%)

由图5中面流线可以看到插板下游存在下洗气流，这会导致低速区中的次涡向下运动，在此过程中由于受到圆形管壁的作用，次涡会逐渐向管道对称面运动。由于两个次涡的旋向相反所以在相遇后会逐渐掺混消失，管道出口位置已经没有明显的次涡结构。

2.2 插板下游紊流度沿程发展规律

图6为插板下游沿程紊流度云图，4个截面与插板轴向距离依次为0.5D、1.5D、2.5D和3.5D。可以看到插板下游紊流度的主要来源是速度梯度较高的过渡区，插板的角涡区和下部低速区也对紊流度的产生有一定贡献，但作用较小；插板上部的高速区由于未受到扰动，对紊流度的产生几乎没有任何贡献。板下游距离较近位置由于回流区影响明显，低速区内靠近对称面位置紊流度较大，两个次涡对应位置的紊流度较低。插板下游距离较近位置紊流度分布集中，随着流动发展会逐渐掺混扩散，管道中部高紊流度区逐渐向上发展，管道两侧角涡区和过渡区会逐渐掺混。在板下游1.5D距离后，会形成管道上部和下部两个低紊流度区；板下游约2.5D位置，会在管道中间形成“W”型的高紊流度区。在管道出口位置紊流度的分布已经较为均匀，没有过于明显的高紊流度区。

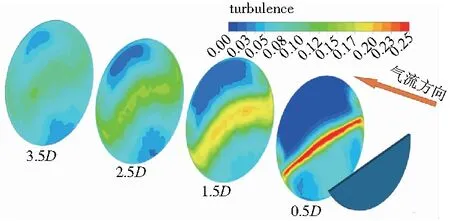
图6 插板下游沿程紊流度分布云图(Main=0.347，H=36%)

图7为不同插板高度和进口马赫数工况下插板下游面平均紊流度的沿程变化情况，横坐标为截面与插板后缘面的无量纲轴向距离，即实际距离与管道直径的比值。可以发现不同情况下紊流度的沿程发展规律基本相同，存在一个先增大后减小的过程；进口马赫数和插板高度对靠近插板位置的紊流度几乎没有影响，插板下游会出现紊流度快速增长，随后会有一个较小的平缓变化段，平缓变化段后紊流度会随距离增加呈线性下降。紊流度最大值的位置随进口马赫数或插板高度增加均会逐渐向下游移动。

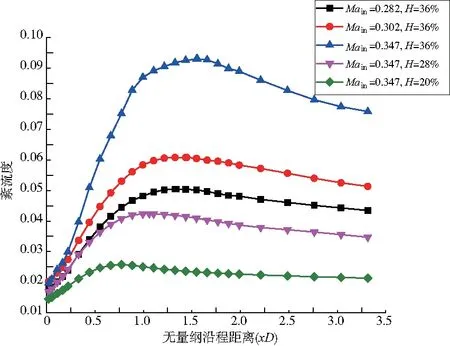
图7 插板下游面平均紊流度沿程变化

图8为不同插板高度和进口马赫数时管道对称面马赫数云图和紊流度等值线，轴向长度只取到了板下游约1.65D位置，图中黑线表示平均紊流度最大的截面。从图中可以看到插板下游较近位置的紊流度主要分布在过渡区，对比图7中紊流度沿程发展过程可以发现，紊流度快速增长区对应了过渡区前部有较大法向速度梯度的位置，随着高速区和低速区气流掺混，过渡区的速度梯度逐渐减小进而不再对紊流度的生成有贡献。

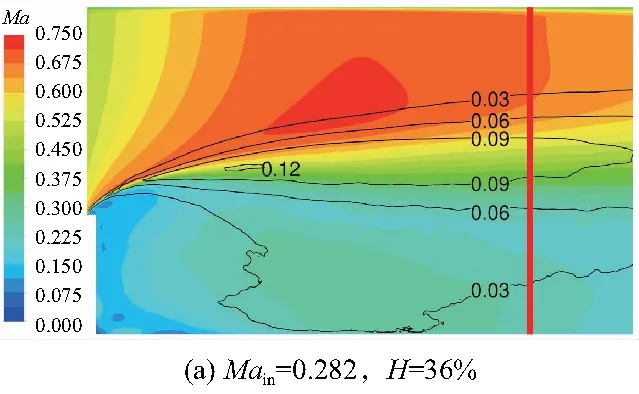
图8 管道对称面马赫数云图和紊流度分布等值线

2.3 插板下游总压恢复系数沿程发展规律

图9为插板下游各截面的总压恢复系数云图。可以发现插板下游总压损失主要由插板下游的回流区产生；插板的角涡区也会产生一定的总压损失，但对截面总压损失贡献较小，在出口位置对总压分布已经没有明显影响。插板下游0.5D位置，上部流通区和下部低速区有很明显的分界线；随后两区气流会逐渐掺混，在管道出口截面上部和下部会分别出现高总压区和低总压区，两区之间的总压近似呈线性变化。

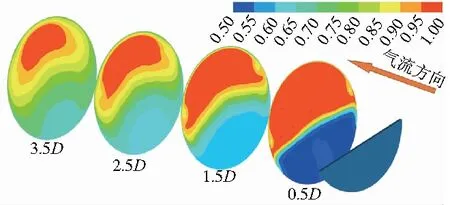
图9 插板下游总压恢复系数沿程分布云图(Main=0.347，H=36%)

图10为插板下游总压恢复系数沿程变化曲线图，可以看到面平均总压恢复系数随着轴向距离增加会先经历一个总压快速下降过程，然后总压降低速度逐渐减小；但是在进口马赫数0.347，插板高度为36%时，插板下游1.5D～2D位置会出现总压突然降低的情况。

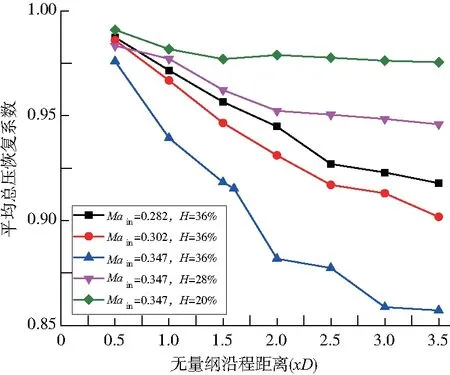
图10 插板下游面平均总压恢复系数沿程变化

对比图11中管道对称面的总压恢复系数云图和流线图可以发现，总压快速下降的距离与插板下游回流区的长度有一定的对应关系；在回流区下游，管道内气流的掺混强度减弱，使得总压降低梯度减缓。在插板高度较高、进口马赫数较大时，主回流区后还会产生一个较小的回流区，小回流区的轴向位置与上文所述的总压突降位置基本重合，可能是造成总压突降的原因。

图11 管道对称面总压恢复系数云图和流线图

对比图11中各情况，可以发现回流区的长度主要受插板高度的影响，进口马赫数对此几乎没有影响；在圆管的三维流动中，插板高度降低会对板下游回流区大小产生显著的影响，所以插板高度变化对总压变化的影响更明显。图11(c)中没有看到插板上部超声速区后由于激波产生的总压损失，这可能是由于插板下游管道中气流有较大的径向速度，高低速区之间的气流掺混使得超声速气流逐渐减速，并未在超声速区之后产生较强的激波。