某工程车轴箱轴承内圈装反对轴承寿命的影响分析
2022-06-24雷亚南黄志辉秦晓特郑志伟穆云飞何建明
雷亚南,黄志辉,秦晓特,郑志伟,穆云飞,何建明
(西南交通大学 牵引动力国家重点实验室,四川 成都 610031)
0 引言
轴箱轴承作为转向架重要部件,不仅要承受车辆较大的径向载荷,还要传递轴向载荷,其性能优劣将直接影响寿命以及车辆的运行安全。在轴承实际安装过程中,由于工人操作失误,轴承内圈出现装反的情况,导致滚子部分区域处于悬空状态,影响了轴承的载荷分布情况及寿命,所以有必要对内圈装反的轴承进行受力分析与寿命评估。
1 双列圆柱滚子轴承接触应力计算
1.1 轴承参数
轴承采用双列圆柱滚子轴承,由NJP 2228Q1/C4S0型号轴承以及NJ2228Q1/C4S0型号轴承组合而成。此轴承具有结构紧凑、承载能力大及受负荷后变形小等优点,一般用于工程车上。双列圆柱滚子轴承三维模型及部分剖面图如图1-图2所示,轴承参数如表1所示。

图1 双列圆柱滚子轴承三维模型

图2 双列圆柱滚子轴承部分剖面图

表1 轴承参数
1.2 轴承径向载荷分布情况
根据轴承的受载特点与径向游隙情况,双列圆柱滚子轴承只有上半圈的部分滚子承受载荷。依据Stribeck理论[1],双列圆柱滚子轴承径向载荷分布情况如图3所示。

图3 双列圆柱滚子轴承径向载荷分布情况
在图3中,选取与轴承内圈圆心成120°的外圈表面作为承载面,受载表面压力呈cos函数分布,压力分布函数pi为
pi=Ccos(αβ-1π)
(1)

径向总载荷P为
(2)
式中:R表示外圈半径,mm;L表示外圈承载面宽度,mm。
轴箱轴承受载的是转向架一系簧上质量,轴承当量动载荷Fr[2]为
(3)
式中:A为轴质量,取23000kg;GR为簧下质量,取2100kg;g为9.81m/s2;fz为垂向动载系数,取1.5;fa为载荷系数,取1;iR为每轮对上的轴承数量,取2。
假定径向总载荷P与轴承当量动载荷Fr相同,联立式(1)-式(3)得到轴承外圈受载面的压力分布函数pi为
pi=6.5cos(1.5α)
(4)
1.3 Hertz弹性接触理论接触应力计算
Hertz弹性接触理论计算接触应力的假设为[3]:
1)接触物体产生弹性变形遵从虎克定律;
2)负载与接触表面垂直,且接触区域的摩擦系数为0;
3)接触面的曲率半径远大于接触宽度;
4)接触体的直径远小于其长度。
根据Hertz公式可得:
(5)
(6)
式中:δH为接触应力,MPa;F为法向接触外载荷,N;L为接触线长度,mm;ρ1、ρ2分别等于两接触物体节点的曲率半径,mm;正号用于外接触,负号用于内接触;E1、E2分别为两圆柱体材料的弹性模量,MPa;μ1、μ2分别为两圆柱体材料的泊松比;a为接触半宽,mm。
1.4 有限元接触应力计算
1)轴承有限元模型的建立
根据轴承的承载特点与接触特性,轴承最顶端的圆柱滚子相比于其他滚子所受径向载荷、应力以及变形量最大,因此选取轴承的最顶端滚子以及与之相接触的内外圈部分,即轴承1/15的最顶端部分作为研究对象,所研究轴承部分的三维模型如图4所示。
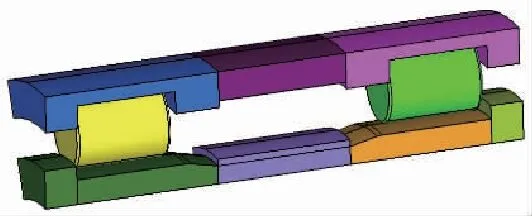
图4 轴承部分三维模型
2)网格划分与接触设置
将研究模型导入到有限元软件中,并对其进行网格划分及接触设置。通过网格收敛性分析,接触区域的网格大小选为0.1mm,其他非关键部位的网格大小取1~2mm,网格单元采用solid186单元,有限元模型的单元数和节点数分别为635205个和753832个。滚子与内外圈的接触采用面面接触,滚子的接触表面作为目标面,采用targe170单元,内外圈的接触表面作为接触面,采用contact173单元,共设置4对接触,轴承部分有限元模型如图5所示。

图5 轴承部分有限元模型
3)边界条件
根据轴承的受力情况,在NJP以及NJ型号轴承外圈承载表面上施加cos函数压力,轴承载荷施加位置如图6所示。轴承内圈与车轴过盈配合,因此固定约束施加在内圈以及内隔环的表面上;由于轴承受到垂向载荷且有垂向位移,需释放其z向自由度,对NJP和NJ型号轴承外圈侧表面以及滚子的两侧表面的中心节点约束其横向与纵向的自由度,即x与y方向的自由度[4];轴承约束施加位置如图7所示。

图6 轴承载荷施加位置

图7 轴承约束施加位置
1.5 两种方法接触应力结果对比
由于轴承具有对称性,所以以下只列出NJ型号轴承的接触应力云图。有限元方法所得到的滚子与外圈以及滚子与内圈的接触应力云图如图8-图9所示。

图8 滚子与外圈的接触应力云图

图9 滚子与内圈的接触应力云图
从图8可知,外圈与滚子在接触表面上受力不均匀,接触表面中间部分与两侧部分接触应力相差较大,且右侧部分接触应力的集中系数比左侧部分大,这与NJ轴承外圈所受的载荷位置、外圈的形状以及滚子边缘效应有关。从图9可知,内圈与滚子在接触表面上受力较均匀,但还是存在应力集中现象,这与滚子与外圈的受力不均以及滚子的边缘效应有关。
运用Hertz公式与有限元方法所得到的接触应力和半宽结果对比如表2所示。

表2 两种方法结果对比
从表2可知,有限元方法计算滚子与外圈的接触半宽与Hertz公式计算结果的比值达到了1.5,有限元方法计算滚子与内圈的接触半宽与Hertz公式计算结果的比值达到了2.19。原因分析如下:1)由轴承的尺寸参数可知,接触体的长度与直径的比值为2倍左右,而Hertz理论假定接触体初始情况为线接触,接触体直径远小于其长度,此假定会导致接触体受载后接触半宽小于实际情况;2)Hertz接触理论视接触体为均匀受载,没有考虑外圈受载的复杂性导致的接触面积变化。
在载荷相同的情况下,接触半宽与接触应力成反比。在有限元方法计算的滚子与外圈的接触半宽与Hertz公式计算结果的比值达到1.5的情况下,有限元计算的滚子与外圈的接触应力与Hertz理论计算的结果却比较接近,原因在于外圈受载位置以及形状导致的接触应力集中和边缘效应。
Hertz弹性接触理论由于受到各种假设的限制,不能考虑轴承受载以及形状的复杂性,因此采用有限元方法对内圈装反的轴承进行建模分析。
2 内圈装反对轴承寿命的影响
在轴承实际安装过程中,由于工人操作失误,NJP轴承内圈出现装反的情况,即NJP轴承内圈有斜角的一侧本应装在内侧,却安装在了外侧,内圈装反轴承部分模型如图10所示。NJP轴承的滚子右侧下表面没有和NJP轴承内圈接触,导致滚子的悬空,对滚子与内圈的安全运行非常不利,所以有必要对其进行寿命分析。

图10 内圈装反轴承三维示意图
由于只有NJP轴承的内圈装反,所以只对NJP轴承在正确安装与内圈装反时的寿命进行对比分析。
2.1 正确安装轴承寿命计算
采用ISO 281∶2007(E)标准[5]计算轴承基本额定寿命L10:
(7)
式中:L10为基本额定寿命,百万转;Cr为基本额定动载荷,值为1870kN;Fr为当量动载荷,值为142.34kN;p为寿命指数,取10/3[6]。
理论计算寿命S为
S=L10·D·π
(8)
式中:D为车轮轮径(半磨耗),取880mm。得到正确安装轴承的计算寿命里程为14.8×106km。
2.2 内圈装反轴承寿命计算
由于NJP轴承的内圈装反,正确安装的轴承寿命公式不适用于内圈装反轴承寿命计算。根据内圈装反轴承的受力特点,滚子与外圈的接触长度不变,而滚子与内圈的接触长度变短,即滚子与内圈在接触线上受载不均,视为滚子与内圈出现偏载情况。利用有限元方法得到了在正确安装以及内圈装反两种情况下轴承滚子接触表面层区域内切应力分布,结合正确安装轴承理论计算寿命,根据L-P寿命理论和ASH法则得到内圈装反轴承的寿命[7],内圈装反轴承寿命Lm为
(9)
式中:La为正确安装轴承寿命;lm、la分别为内圈装反及正确安装轴承接触区域有效长度,mm;zom、zoa分别为内圈装反及正确安装轴承疲劳切应力深度,mm;τom、τoa分别为内圈装反及正确安装轴承最大切应力,GPa;e为weibull斜率,取2;h为切应力深度—寿命系数,取2.33;c为切应力寿命系数,取10.33。
2.3 正确安装与内圈装反轴承寿命结果对比
在同样的有限元建模方法,即相同的网格大小、接触设置以及边界条件下,得到了正确安装与内圈装反轴承滚子、内圈以及外圈的切应力分布情况。由于滚子与外圈接触受力情况比滚子与内圈的情况恶劣,因此以下只列出了滚子与外圈接触时的切应力分布情况。正确安装与内圈装反轴承情况下的滚子、内圈与外圈的切应力云图如图11-图16所示。正确安装与内圈装反轴承切应力分布情况及寿命结果对比如表3所示。

图11 正确安装轴承滚子的切应力云图

图12 内圈装反轴承滚子的切应力云图

图13 正确安装轴承内圈的切应力云图

图14 内圈装反轴承内圈的切应力云图
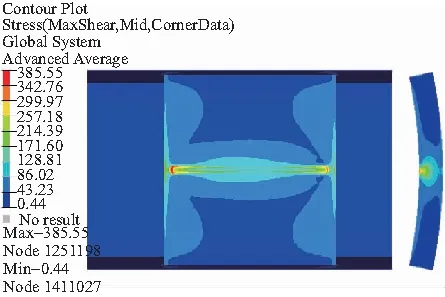
图15 正确安装轴承外圈的切应力云图

图16 内圈装反轴承外圈的切应力云图

表3 正确安装与内圈装反轴承切应力分布情况及寿命结果对比
HARRIS在L-P理论的基础上对寿命进行了改进[8],考虑了滚子的寿命、轴承整体寿命与内圈、外圈以及滚子寿命的关系如公式(10)所示。
(10)
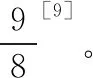
综合表3及公式(10)可得,内圈装反轴承寿命为302.55×104km,仅是正确安装轴承寿命的20.44%,说明轴承内圈装反对轴承的寿命影响极大。
3 结语
1)分别采用Hertz弹性接触理论和有限元方法对正确安装的双列圆柱滚子轴承接触应力进行计算,对比分析了两种方法下滚子与外圈以及滚子与内圈的接触应力分布情况。Hertz弹性接触理论由于受到各种假设的限制,不能考虑轴承受载以及形状的复杂性,因此采用有限元方法对内圈装反的轴承进行建模分析。
2)采用ISO国际标准理论算法,确定了正确安装工况下轴承寿命。根据L-P寿命理论和ASH法则得到了内圈装反轴承寿命。以轴承整体寿命作为评估对象,内圈装反轴承寿命为302.55×104km,仅仅是正确安装轴承寿命的20.44%。
